problema 1 problema 2 problema 3

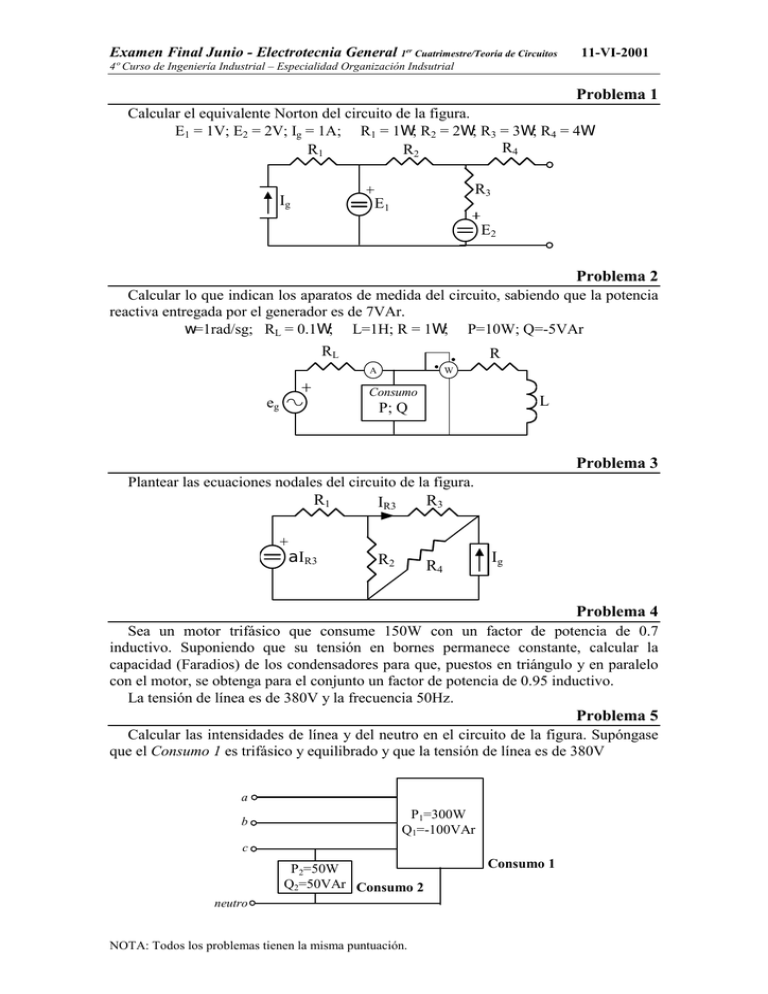
Examen Final Junio - Electrotecnia General 1er Cuatrimestre/Teoría de Circuitos
11-VI-2001
4º Curso de Ingeniería Industrial – Especialidad Organización Indsutrial
Problema 1
Calcular el equivalente Norton del circuito de la figura.
E1 = 1V; E2 = 2V; Ig = 1A; R1 = 1:; R2 = 2:; R3 = 3:; R4 = 4:
R4
R1
R2
Ig
R3
E1
E2
Problema 2
Calcular lo que indican los aparatos de medida del circuito, sabiendo que la potencia
reactiva entregada por el generador es de 7VAr.
Z=1rad/sg; RL = 0.1:; L=1H; R = 1:; P=10W; Q=-5VAr
RL
R
A
W
Consumo
eg
L
P; Q
Problema 3
Plantear las ecuaciones nodales del circuito de la figura.
R1
DIR3
IR3
R3
R2
R4
Ig
Problema 4
Sea un motor trifásico que consume 150W con un factor de potencia de 0.7
inductivo. Suponiendo que su tensión en bornes permanece constante, calcular la
capacidad (Faradios) de los condensadores para que, puestos en triángulo y en paralelo
con el motor, se obtenga para el conjunto un factor de potencia de 0.95 inductivo.
La tensión de línea es de 380V y la frecuencia 50Hz.
Problema 5
Calcular las intensidades de línea y del neutro en el circuito de la figura. Supóngase
que el Consumo 1 es trifásico y equilibrado y que la tensión de línea es de 380V
a
b
P1=300W
Q1=-100VAr
c
P2=50W
Q2=50VAr Consumo 2
neutro
NOTA: Todos los problemas tienen la misma puntuación.
Consumo 1
Examen Final Septiembre- Electrotecnia General 1er Cuatrimestre/Teoría de Circuitos
12-IX-2001
4º Curso de Ingeniería Industrial – Especialidad Organización Industrial
Calcular el equivalente Norton
entre los terminales A y B del
circuito de la figura. Sabiendo que:
E = 12V; Ig = 1A;
R1 = 1:; R2 = 2:; R3 = 3:;
R4 = 4:; R5 = 5:
Problema 1
R1
A
R3
Ig
E
R4
R2
R5
B
Problema 2
Calcular los valores de
R2 y L2, así como las
medidas del amperímetro y
voltímetro sabiendo que:
RL
VA1
VA2
W2
A
R2
R1
eg
V
Z=1rad/sg; RL = 0.1:
R1 = 1:; L1 = 2H
VA1 = 6VAr
W2 = 2W; VA2 = 2VAr
L2
L1
Problema 3
Plantear las ecuaciones de mallas del
circuito de la figura.
E1
R1
IR3
R3
R2
DIR3
E3
E2
Problema 4
Sea un motor trifásico con una potencia aparente de 150VA y un factor de potencia
de 0.7 inductivo. Suponiendo que su tensión en bornes permanece constante, calcular la
capacidad (Faradios) de los condensadores para que, puestos en triángulo y en paralelo
con el motor, se obtenga para el conjunto un factor de potencia de 0.95 inductivo.
La tensión de línea es de 380V y la frecuencia 50Hz.
Problema 5
a
X=2:
R=1:
P=300W
Q=-100VAr
Calcular las intensidades de línea
Supóngase que el consumo trifásico (P y Q)
está equilibrado y que la tensión de línea es
de 380V.
b
c
NOTA: Todos los problemas tienen la misma puntuación.
Examen Final Diciembre- Electrotecnia General 1er Cuatrimestre / Teoría de Circuitos 18-XII-2001
4º Curso de Ingeniería Industrial – Especialidad Organización Industrial
Calcular el equivalente Norton
entre los terminales A y B del
circuito de la figura. Sabiendo que:
E = 12V; Ig = 1A;
R1 = 1:; R2 = 2:; R3 = 3:;
R4 = 4:; R5 = 5:
Problema 1
R1
A
R3
Ig
E
R4
R2
R5
B
Problema 2
Calcular los valores de
R2 y L2, así como las
medidas del amperímetro y
voltímetro sabiendo que:
RL
VA1
VA2
W2
A
R2
R1
eg
V
Z=1rad/sg; RL = 0.1:
R1 = 1:; L1 = 2H
VA1 = 6VAr
W2 = 2W; VA2 = 2VAr
L2
L1
Problema 3
Plantear las ecuaciones de mallas del
circuito de la figura.
E1
R1
IR3
R3
R2
DIR3
E3
E2
Problema 4
Sea un motor trifásico con una potencia aparente de 150VA y un factor de potencia
de 0.7 inductivo. Suponiendo que su tensión en bornes permanece constante, calcular la
capacidad (Faradios) de los condensadores para que, puestos en triángulo y en paralelo
con el motor, se obtenga para el conjunto un factor de potencia de 0.95 inductivo.
La tensión de línea es de 380V y la frecuencia 50Hz.
Problema 5
a
X=2:
R=1:
P=300W
Q=-100VAr
Calcular las intensidades de línea
Supóngase que el consumo trifásico (P y Q)
está equilibrado y que la tensión de línea es
de 380V.
b
c
NOTA: Todos los problemas tienen la misma puntuación.
1er Parcial- Electrotecnia General
09-III-2002
1er Cuatrimestre / Teoría de Circuitos
4º Curso de Ingeniería Industrial – Especialidad Organización Industrial
Problema 1
XC=10:
VA
W
A
R
VB
VA
X
Calcular los valores de R y X, así
como las medidas de los voltímetros
(VA y VB), sabiendo que las medidas
en el resto de los aparatos son:
A =1A
VA = 100 VAr
W = 100 W
Problema 2
Plantear las ecuaciones de
mallas del circuito de la figura.
R1
E1
R3
R4
kUR2
UR2
R2
E2
Problema 3
R
C
L
Calcular los valores de R y L de una lámpara de descarga
cuyo factor de potencia es 0,5 inductivo, de la cual se sabe que
con un condensador de 5PF tiene un factor de potencia de 0,9
inductivo. Suponer que la tensión de red es de 220V y la
frecuencia de 50Hz.
Problema 4
Calcular las intensidades de línea del circuito de
la figura. Supóngase que el sistema está equilibrado
y que la tensión de línea es de 380V.
a
b
c
P = 300W
Q = 300VAr
Z=1:
cos M = 0,5 (ind)
Problema 5
Si tenemos un conjunto de 13 motores con una potencia de 1kW cada uno y cuyo
factor de potencia es de 0,5 inductivo, calcular la batería de condensadores que se
necesitaría para que el factor de potencia del conjunto fuese 0,95 inductivo.
La tensión de línea es de 380V y los condensadores de los que se disponen tienen las
siguientes características:
Tensiones nominales disponibles (V): 230 – 400 - 415
Potencias nominales disponibles (kVAr): 5 - 7,5 – 10 - 12,5 - 15
NOTA: Todos los problemas tienen la misma puntuación. Es necesario obtener una calificación de
2 sobre 10 en cada uno de los problemas.
TIEMPO: 3 horas
Final JUNIO- Electrotecnia General
1er Cuatrimestre / Teoría de Circuitos
10-VI-2002
4º Curso de Ingeniería Industrial – Especialidad Organización Industrial
Problema 1
Calcular potencia reactiva nominal la batería de
condensadores que se ha de poner en paralelo con el circuito
de la figura para que el factor de potencia del conjunto sea
0.9 inductivo. Los condensadores de los que se dispone
tienen una tensión nominal de los condensadores 240V.
Calcular la intensidad en el amperímetro (A), antes y
después de poner la batería, sabiendo que la tensión del
voltímetro (V1) es 220 V
A
V1
R = 0.5 :
P=100kW
cos M=0.9 ind
X = 0.5 :
Problema 2
Calcular el equivalente Thevenin entre los terminales “a”
y “b” del circuito de la figura, sabiendo que:
R1 = R2 = 1 :
Ug = 5 V; Ig = 2 A; E = 1/2
U1
a
R1
R2
Ug
EU1
Ig
b
Problema 3
R=0.1: X=0.1:
VAr2
VAr1
A1
W2
carga
P, Q
V2
V1
Calcular lo que indican los aparatos de medida
A1, V2, VAr2 y W2 sabiendo las siguientes
medidas:
V1 = 220V; VAr1 = 10 VAr
Se sabe además que el factor de potencia del
circuito visto desde la fuente es de 0.9 inductivo.
Problema 4
Calcular las intensidades de línea a la entrada del circuito
indicado y así como las potencias P1 y Q1, sabiendo que la
potencia aparente que consume el conjunto es de 10 kVA con
un factor de potencia de 0.9 capacitivo. Supóngase que el
sistema está equilibrado y que la tensión de línea es de 380V.
a
P2 = 5 kW
Q2 = 5 kVAr
b
c
P1; Q1
Problema 5
a
A1
X=1:
R=3:
b
A2
Calcular las medidas de los amperímetros A1, A2
y AN en el circuito de la figura. Se sabe que es un
sistema trifásico equilibrado con una tensión de
línea (Uab) de 380 V
c
N
Z = 1.41 :
cos M = 0.707 ind
AN
CALIFICACIÓN:
DURACIÓN:
Todos los problemas tienen la misma puntuación. Es necesario obtener una calificación de 2 sobre 10
en cada uno de los problemas.
3 horas
Final JUNIO- Electrotecnia General
03-VII-2002
1er Cuatrimestre / Teoría de Circuitos
4º Curso de Ingeniería Industrial – Especialidad Organización Industrial
Problema 1
Calcular la intensidad i(t) del circuito de la figura sabiendo
que los valores de los componentes son:
R = 10 !, C = 500 "F y L = 1 mH
Además, la tensión medida con un osciloscopio tiene la
expresión:
i(t)
R
u(t)
L
C
u # t $ % 2 & 220 & cos #100't ( ' 3$ voltios
Problema 2
Calcular el equivalente Thevenin entre los terminales
“a” y “b” del circuito de la figura, sabiendo que:
R1 = R2 = R3 = 1 !
Ug = 2 V; Ig = 3 A; ) = 1/2
U1
R1
a
R2
R3
Ug
)U1
Ig
b
Problema 3
R
VAr1
A1
W
VAr2
A2
V1
V2
carga
P, Q
X
Calcular lo que indican los aparatos de medida
A2, V2 y VAr2 así como el valor de R sabiendo las
siguientes medidas:
V1 = 220V; A1 = 10 A
W = 2000 W; VAr1 = 0 VAr
Se sabe además que la reactancia X de la bobina
es 20!
Problema 4
Calcular la capacidad de los condensadores así como su
potencia reactiva nominal, para que en el circuito de la figura
el factor de potencia del conjunto sea 0.9 inductivo. Supóngase
que el sistema está equilibrado y que la tensión de línea es de
380V.
La tensión nominal de la batería de condensadores es 440V.
a
P = 5 kW
Q = 10 kVAr
b
c
R = 10 !
C
Problema 5
a
A1
Calcular las medidas de los amperímetros A1,
A2 y A3 en el circuito de la figura. Se sabe que es
R = 30 !
un sistema trifásico equilibrado con una tensión de
línea (Uab) de 380 V
A
XL=1! RL=1!
b
2
c
Z = 15 !
cos * = 0.5 ind
A3
CALIFICACIÓN:
DURACIÓN:
Todos los problemas tienen la misma puntuación. Es necesario obtener una calificación de 2 sobre 10
en cada uno de los problemas.
3 horas
Final SEPTIEMBRE- Electrotecnia General
11-IX-2002
1er Cuatrimestre / Teoría de Circuitos
4º Curso de Ingeniería Industrial – Especialidad Organización Industrial
Problema 1
Calcular potencia reactiva nominal la batería de
condensadores que se ha de poner en paralelo con el circuito
de la figura para que el factor de potencia del conjunto sea
0.95 inductivo. Los condensadores de los que se dispone
tienen una tensión nominal de los condensadores 240V.
Calcular la intensidad en el amperímetro (A), antes y
después de poner la batería, sabiendo que la tensión del
voltímetro (V1) es 220 V
A
R = 0.5 :
P2=10 kW
cos M2=0.7 cap
X = 0.5 :
V1
Problema 2
Calcular el equivalente Norton entre los terminales
“a” y “b” del circuito de la figura, sabiendo que:
R1 = R2 = R3 = R4 = R5 = 1 :
Ig = 2 A; E = 1/2
R1
EUR3
R4
R5
Ig
R3
a
UR3
b
R2
Problema 3
UR1
R3
R1
R2
Eg
Plantear las ecuaciones nodales en su forma
matricial para el circuito de la figura.
DUR1
Ig
R4
Problema 4
Calcular lo que indican los aparatos de
medida V1, V2, A1 y W3 así como los
valores de RD y XD sabiendo las siguientes
medidas:
W1 = 10 W, W2 = 1W y VAr1 = 5 VAr
R=0.1: X=0.1:
W1
A1
VAr1
W2
W3
RD
V1
V2
XD
Problema 5
a
A1
X=1:
R=3:
b
A2
Calcular las medidas de los amperímetros A1, A2
y AN en el circuito de la figura. Se sabe que es un
sistema trifásico equilibrado con una tensión de
línea (Uab) de 380 V
c
N
Z = 1.41 :
cos M = 0.707 ind
AN
CALIFICACIÓN:
DURACIÓN:
Todos los problemas tienen la misma puntuación. Es necesario obtener una calificación de 2 sobre 10
en cada uno de los problemas.
3 horas
Final DICIEMBRE - Electrotecnia General
02-XII-2002
1er Cuatrimestre / Teoría de Circuitos
4º Curso de Ingeniería Industrial – Especialidad Organización Industrial y Mecánica
Problema 1
RL
Calcular lo que indican los aparatos
de medida del circuito, sabiendo que la
potencia reactiva indicada por el
varímetro es de 7VAr.
L
Z = 1rad/sg
RL = 0.1:; L=1H; R = 1:
P=10W; Q=-5VAr
R
VAr
A
W
Consumo
Eg
V
P; Q
Problema 2
Plantear las ecuaciones de mallas del
circuito de la figura.
R1
E1
IR1
R3
R4
kIR1
R2
E2
Problema 3
Sea un motor trifásico que consume 150W con un factor de potencia de 0.7 inductivo.
Suponiendo que su tensión en bornes permanece constante, calcular la capacidad (Faradios) de los
condensadores para que, puestos en triángulo y en paralelo con el motor, se obtenga para el
conjunto un factor de potencia de 0.95 inductivo.
La tensión de línea es de 380V y la frecuencia 50Hz.
Problema 4
a
XL=1:
A1
R
b
c
R
XL
XL
A3
Z
Z
n
2
Z = 15 :
cos M = 0.5 inductivo
An
CALIFICACIÓN:
DURACIÓN:
Z
Calcular las medidas de los
amperímetros An, A1, A2 y A3 en el
R = 30 : circuito de la figura. Se sabe que es
un sistema trifásico equilibrado con
A
una tensión de línea (Uab) de 380 V y
que la impedancia Z está definida
por:
Todos los problemas tienen la misma puntuación. Es necesario obtener una calificación de 2 sobre 10
en cada uno de los problemas.
2 horas y 15 min
1er Parcial - Electrotecnia General
08-III-2003
1er Cuatrimestre / Teoría de Circuitos
4º Curso de Ingeniería Industrial – Especialidad Mecánica
Problema 1
En el circuito de la figura calcular la
medida del voltímetro y el valor de la
impedancia Z, sabiendo que:
XL = 0.2!
W
A
Eg
V
R = 1!
Z
cos * = 0.8 ind
Amperímetro A = 1A
Vatímetro W = 2W
Problema 2
Plantear las ecuaciones de mallas del circuito de la figura.
UR1
E
Ig
R1
)UR1
R2
R4
R3
Problema 3
Sea un motor trifásico que consume 4kW y con una intensidad de 10A. Suponiendo que su
tensión en bornes permanece constante, calcular la potencia reactiva nominal de la batería de
condensadores para que, puesta en paralelo con el motor, se obtenga para el conjunto un factor de
potencia de 0.95 inductivo.
La tensión de línea es de 380V y la frecuencia 50Hz.
Para la batería de condensadores escoger una de las siguientes tensiones nominales: 230V, 400V
y 440V.
Problema 4
a
Aa
b
Ab
c
Ac
P = 1000 W
Q = 500 VAr
Calcular las medidas de los amperímetros
An, Aa, Ab y Ac en el circuito de la figura. Se
sabe que es un sistema trifásico equilibrado de
tensiones con una tensión de línea (Uab) de
380 V.
P´ = 200 W
cos *´ = 0.5 cap
n
An
CALIFICACIÓN:
DURACIÓN:
Todos los problemas tienen la misma puntuación. Es necesario obtener una calificación de 2 sobre 10
en cada uno de los problemas.
2 horas y 30 min
1er Parcial - Electrotecnia General
15-III-2003
1er Cuatrimestre / Teoría de Circuitos
4º Curso de Ingeniería Industrial – Especialidad Organización Industrial
Problema 1
XL = 0.2!
W
A
Eg
V
P = 100 W
Q = 100 VAr
R = 100!
En el circuito de la figura calcular la
medida del voltímetro y el ámperímetro
sabiendo que el Vatímetro indica un
consumo de 200W
Problema 2
Calcular el equivalente Thevenin del circuito de la figura.
a
)U
Ig
U
R
b
Problema 3
Sea un motor trifásico que consume 4kW con una potencia aparente de 7000VA. Suponiendo
que su tensión en bornes permanece constante, calcular la capacidad de la batería de condensadores
para que, puestos en paralelo con el motor, se obtenga para el conjunto un factor de potencia de
0.95 inductivo.
La tensión de línea es de 380V y la frecuencia 50Hz.
Problema 4
a
Aa
R = 300 !
b
Ab
c
Ac
R
R
Calcular las medidas de los amperímetros
An, Aa, Ab y Ac en el circuito de la figura.
Se sabe que es un sistema trifásico
equilibrado con una tensión de línea (Uab)
de 380 V.
P´ = 1500 W
cos *´ = 0.9 cap
n
An
CALIFICACIÓN:
DURACIÓN:
Todos los problemas tienen la misma puntuación. Es necesario obtener una calificación de 2 sobre 10
en cada uno de los problemas.
2 horas y 30 min
1er Parcial - Electrotecnia General
09-VI-2003
1er Cuatrimestre / Teoría de Circuitos
4º Curso de Ingeniería Industrial – Especialidad Mecánica
Problema 1
XL = 0.2Ω
W
A
Eg
V
P = 100 W
Q = 100 VAr
R = 100Ω
En el circuito de la figura calcular la
medida del voltímetro y el ámperímetro
sabiendo que el Vatímetro indica un
consumo de 200W
Problema 2
Calcular el equivalente Thevenin del circuito de la figura.
a
βU
Ig
U
R
b
Problema 3
Sea un motor trifásico que consume 4kW con una potencia aparente de 7000VA. Suponiendo
que su tensión en bornes permanece constante, calcular la capacidad de la batería de condensadores
para que, puestos en paralelo con el motor, se obtenga para el conjunto un factor de potencia de
0.95 inductivo.
La tensión de línea es de 380V y la frecuencia 50Hz.
Problema 4
a
Aa
R = 300 Ω
b
Ab
c
Ac
R
R
Calcular las medidas de los amperímetros
An, Aa, Ab y Ac en el circuito de la figura.
Se sabe que es un sistema trifásico
equilibrado con una tensión de línea (Uab)
de 380 V.
P´ = 1500 W
cos ϕ´ = 0.9 cap
n
An
CALIFICACIÓN:
DURACIÓN:
Todos los problemas tienen la misma puntuación. Es necesario obtener una calificación de 2 sobre 10
en cada uno de los problemas.
2 horas y 15 min
1er Parcial - Electrotecnia General
9-VI-2003
1er Cuatrimestre / Teoría de Circuitos
4º Curso de Ingeniería Industrial – Especialidad Organización Industrial
Problema 1
En el circuito de la figura calcular la
medida del voltímetro y el valor de la
impedancia Z, sabiendo que:
XL = 0.2Ω
W
A
Eg
V
R = 1Ω
Z
cos ϕ = 0.8 ind
Amperímetro A = 1A
Vatímetro W = 2W
Problema 2
Plantear las ecuaciones de mallas del circuito de la figura.
UR1
E
Ig
R1
βUR1
R2
R4
R3
Problema 3
Sea un motor trifásico que consume 4kW y con una intensidad de 10A. Suponiendo que su
tensión en bornes permanece constante, calcular la potencia reactiva nominal de la batería de
condensadores para que, puesta en paralelo con el motor, se obtenga para el conjunto un factor de
potencia de 0.95 inductivo.
La tensión de línea es de 380V y la frecuencia 50Hz.
Para la batería de condensadores escoger una de las siguientes tensiones nominales: 230V, 400V
y 440V.
Problema 4
a
Aa
b
Ab
c
Ac
P = 1000 W
Q = 500 VAr
Calcular las medidas de los amperímetros
An, Aa, Ab y Ac en el circuito de la figura. Se
sabe que es un sistema trifásico equilibrado de
tensiones con una tensión de línea (Uab) de
380 V.
P´ = 200 W
cos ϕ´ = 0.5 cap
n
An
CALIFICACIÓN:
DURACIÓN:
Todos los problemas tienen la misma puntuación. Es necesario obtener una calificación de 2 sobre 10
en cada uno de los problemas.
2 horas y 15 min
Final Septiembre - Electrotecnia General
09-IX-2003
1er Cuatrimestre / Teoría de Circuitos
4º Curso de Ingeniería Industrial – Especialidad Organización Industrial
Problema 1
Calcular el equivalente Norton entre los terminales A y
B del circuito de la figura.
E
R2
R1
A
Ig
B
Problema 2
Calcular lo que indican los aparatos de medida del circuito, sabiendo que la potencia reactiva
entregada por el generador es de 7VAr.
ω=1rad/sg; RL = 0.1Ω; L=1H; R = 1Ω; P=10W; Q=-5VAr
RL
R
A
W
Consumo
eg
P; Q
L
Problema 3
Calcular potencia reactiva nominal la batería de
condensadores que se ha de poner en paralelo con el circuito
de la figura para que el factor de potencia del conjunto sea
0.9 inductivo. Los condensadores de los que se dispone
tienen una tensión nominal de los condensadores 240V.
Calcular la intensidad en el amperímetro (A), antes y
después de poner la batería, sabiendo que la tensión del
voltímetro (V1) es 220 V
A
X = 0.5 Ω
V1
P=100kW
cos ϕ=0.9 ind
Problema 4
XL
a
Aa
XL
b
Ab
c
Ac
CALIFICACIÓN:
DURACIÓN:
XL
R
R
R
Calcular las medidas de los amperímetros Aa, Ab y
Ac así como la potencia activa para el circuito de la
figura, teniendo en en cuenta de que se trata de un
sistema trifásico equilibrado con una tensión de línea
(Uab) de 380 V.
Se sabe que para la resistencia R es de 300 Ω,
mientras que para la bobina XL = 100 Ω.
Todos los problemas tienen la misma puntuación. Es necesario obtener una calificación de 2 sobre 10
en cada uno de los problemas.
2 horas y 15 min
Final Diciembre - Electrotecnia General
04-XII-2003
1er Cuatrimestre / Teoría de Circuitos
4º Curso de Ingeniería Industrial – Especialidades de Mecánica y Organización Industrial
Problema 1
Calcular el equivalente Thevenin y el
equivalente Norton entre los terminales A y B
del circuito de la figura.
E1
R3
A
E2
R1
R2
B
Problema 2
Calcular lo que indican los aparatos de medida del circuito, sabiendo que la
potencia reactiva medida en el varímetro 2 (VAr2) es 7 VAr, y además:
X1 = 2Ω; X2=2Ω; R = 1Ω; P=10W y Q=-5VAr
X1
VAr1
Eg
R
VAr2
A
V
Carga
P; Q
X2
Problema 3
XL
a
Aa
b
Ab
c
Ac
XL
Calcular las medidas de los amperímetros
Aa, Ab, Ac y AN sabiendo que la tensión de línea
es de 400 V, que las reactancias (XL) son de
1000 Ω y que la carga conectada entre los
terminales “c” y “n” tiene un consumo (P) de
100 W con factor de potencia unidad..
XL
P = 100W
cos ϕ = 1
n
AN
Problema 4
Se tiene una carga trifásica que demanda una potencia de 4000 W con una
intensidad de línea de 10 A. Calcular la batería de condensadores que se ha de
poner en paralelo con esta carga para que el factor de potencia del conjunto
(carga + condensadores) sea 0.95 inductivo. Para ello, se dispone de
condensadores con las siguientes características:
- Tensiones nominales disponibles: 230 V, 240 V y 440 V
- Potencias nominales disponibles: 0.2 kVAr, 0.5 kVAr y 1 kVAr
Se sabe que la tensión de línea en la red eléctrica es de 400 V.
CALIFICACIÓN:
DURACIÓN:
Todos los problemas tienen la misma puntuación. Es necesario obtener una calificación de 2 sobre 10
en cada uno de los problemas.
2 horas y 15 min
1er Parcial - Electrotecnia General
29-II-2004
1er Cuatrimestre / Teoría de Circuitos
4º Curso de Ingeniería Industrial – Especialidad Mecánica
Problema 1
Dado el circuito de la figura:
a) Plantear las ecuaciones de mallas.
b) Expresar las corrientes que circulan por cada uno de los
elementos del circuito, en función de las incógnitas del
sistema de ecuaciones anterior.
2Ω
6Ω
1Ω
A
3Ω
B
C
12Ω
1Ω
4A
2Ω
=
9V
5Ω
D
Problema 2
Rg
Calcular el equivalente Thevenin del circuito de la figura.
E
Ig
=
I1
a
βI1
R2
b
Problema 3
Un motor trifásico de 56kW y factor de potencia 0,8 inductivo, se alimenta con una tensión de línea
de 400V 50Hz, por medio de conductores ideales. Calcular:
a) Intensidad de línea.
Suponiendo que su tensión en bornes permanece constante, calcular:
b) Potencia reactiva de la batería de condensadores que se necesita conectar en paralelo con el
motor para obtener un factor de potencia de 0,95 inductivo.
c) Capacidad de los condensadores si la batería de condensadores está configurada en triángulo.
d) Intensidad de línea después de compensar el f.d.p.
Problema 4
a
Aa
b
Ab
c
Ac
P2 = 5 kW
cos ϕ2 = 0,7
Inductivo
Equilibrado
Ac’
A1
N
An’
An
El circuito está conectado en secuencia directa
por medio de conductores ideales, carentes de
impedancias, a un generador ideal equilibrado
con tensión de línea 400V 50Hz.
Calcular el valor de las medidas de los
amperímetros en el circuito de la figura.
P1 = 1 kW
cos ϕ1 = 0,8 cap
CALIFICACIÓN:
DURACIÓN:
Todos los problemas tienen la misma puntuación. Es necesario obtener una calificación de 2 sobre 10
en cada uno de los problemas.
2 horas y 30 min.
1er Parcial - Electrotecnia General
29-II-2003
1er Cuatrimestre / Teoría de Circuitos
4º Curso de Ingeniería Industrial – Especialidad Organización Industrial
Problema 1
Dado el circuito de la figura:
a) Plantear las ecuaciones de mallas.
b) Expresar las corrientes que circulan por cada uno de los
elementos del circuito, en función de las incógnitas del
sistema de ecuaciones anterior.
3Ω
2Ω
6Ω
1Ω
A
B
C
12Ω
1Ω
4A
2Ω
=
9V
5Ω
D
Problema 2
Rg
Calcular el equivalente Thevenin del circuito de la figura.
eg
Ig
=
i1
a
βi1
R2
b
Problema 3
Un motor trifásico de 56kW y factor de potencia 0,8 inductivo, se alimenta con una tensión de línea
de 380V 50Hz, por medio de conductores ideales. Calcular:
a) Intensidad de línea.
Suponiendo que su tensión en bornes permanece constante, calcular:
b) Potencia reactiva de la batería de condensadores que se necesita conectar en paralelo con el
motor para obtener un factor de potencia de 0,95 inductivo.
c) Capacidad de los condensadores si la batería de condensadores está configurada en triángulo.
d) Intensidad de línea después de compensar el f.d.p.
Problema 4
a
Aa
b
Ab
c
Ac
P2 = 5 kW
cos ϕ2 = 0,7
Inductivo
Equilibrado
Ac’
A1
N
An’
An
El circuito está conectado en secuencia directa
por medio de conductores ideales, carentes de
impedancias, a un generador ideal equilibrado
con tensión de línea 380V 50Hz.
Calcular el valor de las medidas de los
amperímetros en el circuito de la figura.
P1 = 1 kW
cos ϕ1 = 0,8 cap
CALIFICACIÓN:
DURACIÓN:
Todos los problemas tienen la misma puntuación. Es necesario obtener una calificación de 2 sobre 10
en cada uno de los problemas.
2 horas y 30 min.
Final Junio - Electrotecnia General
14-VI-2004
1er Cuatrimestre / Teoría de Circuitos
4º Curso de Ingeniería Industrial – Especialidad Mecánica y Organización
Problema 1
Dado el circuito de la figura, donde las medidas
conocidas son:
-
Voltímetro: V = 500 V
-
Vatímetro: W = 1000 W
-
Medida Potencia Aparente: VAz = 900 VA
W
VAZ
A
AR
Az
V
R
Z
Calcular lo que indican los amperímetros A, AR y AZ
sabiendo que el factor de potencia del conjunto formado por la resistencia R y la impedancia Z es
de 0.8 inductivo.
Problema 2
a
Calcular el equivalente Thevenin del circuito de la figura.
Ig
R2
R1
βU1
=
U1
R3
b
Problema 3
Sea una planta industrial con las siguientes cargas:
-
1 motor eléctrico de 1 kW con un factor de potencia de 0.7 inductivo
-
1 consumo de potencia aparente 500 VA con un factor de potencia de 0,95 capacitivo.
Sabiendo que la tensión de línea de la planta es de 400 V, calcular:
a) Intensidad de línea para el conjunto formado por todas las cargas.
Suponiendo que su tensión en bornes permanece constante, calcular:
b) Calcular el número de condensadores que se necesita conectar en paralelo con el conjunto
formado por todas las cargas para obtener un factor de potencia 0.95 inductivo. Se emplearán
para ello condensadores con una tensión nominal de 440 V y potencia reactiva nominal de
100 VAr.
Problema 4
a
Aa
b
Ab
c
Ac
P2 = 5 kW
cos ϕ2 = 0,7
Capacitivo
Equilibrado
Ac2
A1
N
An2
An
El circuito está conectado en secuencia
directa por medio de conductores ideales,
carentes de impedancias, a un generador
ideal equilibrado con tensión de línea 400V
50Hz.
Calcular el valor de las medidas de los
amperímetros en el circuito de la figura.
R1 = 150 Ω
CALIFICACIÓN:
DURACIÓN:
Todos los problemas tienen la misma puntuación. Es necesario obtener una calificación de 2 sobre 10
en cada uno de los problemas.
2 horas y 15 min.
Final Septiembre - Electrotecnia General
13-IX-2004
1er Cuatrimestre / Teoría de Circuitos
4º Curso de Ingeniería Industrial – Especialidad Mecánica
Problema 1
Calcular el equivalente Norton del circuito de la figura.
E1 = 1V; E2 = 2V; Ig = 1A; R1 = 1Ω; R2 = 2Ω; R3 = 3Ω; R4 = 4Ω
R4
R1
R2
Ig
R3
E1
E2
Problema 2
Calcular lo que indican los aparatos de medida del circuito, sabiendo que la potencia reactiva
entregada por el generador es de 7VAr.
ω=1rad/sg; RL = 0.1Ω; L=1H; R = 1Ω; P=10W; Q=-5VAr
RL
R
A
W
Consumo
eg
P; Q
L
Problema 3
Sea un motor trifásico que consume 4kW con una potencia aparente de 7kVA. Suponiendo que
su tensión en bornes permanece constante, calcular la capacidad de la batería de condensadores para
que, puestos en paralelo con el motor, se obtenga para el conjunto un factor de potencia de 0.95
inductivo.
La tensión de línea es de 400V y la frecuencia 50Hz.
Problema 4
a
Aa
R
R = 300 Ω
b
Ab
c
Ac
R
Calcular las medidas de los amperímetros
An, Aa, Ab y Ac en el circuito de la figura.
Se sabe que es un sistema trifásico
equilibrado con una tensión de línea (Uab)
de 400 V.
P´ = 1500 W
cos ϕ´ = 0.9 cap
n
An
CALIFICACIÓN:
DURACIÓN:
Todos los problemas tienen la misma puntuación. Es necesario obtener una calificación de 2 sobre 10
en cada uno de los problemas.
2 horas y 15 min.
Examen Dicembre - Electrotecnia General
17-XII-2004
1er Cuatrimestre / Teoría de Circuitos
4º Curso de Ingeniería Industrial – Especialidad Organización Industrial y Mecánica
Problema 1
En el circuito de la figura calcular la
medida del voltímetro y el valor de la
impedancia Z, sabiendo que:
XL = 0.2Ω
W
A
Eg
V
R = 1Ω
Z
cos ϕ = 0.8 ind
Amperímetro A = 1A
Vatímetro W = 2W
Problema 2
Plantear las ecuaciones de mallas del circuito de la figura.
UR1
E
Ig
R1
βUR1
R2
R4
R3
Problema 3
Sea un motor trifásico que consume 4kW y con una intensidad de 10A. Suponiendo que su
tensión en bornes permanece constante, calcular la potencia reactiva nominal de la batería de
condensadores para que, puesta en paralelo con el motor, se obtenga para el conjunto un factor de
potencia de 0.95 inductivo.
La tensión de línea es de 380V y la frecuencia 50Hz.
Para la batería de condensadores escoger una de las siguientes tensiones nominales: 230V, 400V
y 440V.
Problema 4
a
Aa
b
Ab
c
Ac
P = 1000 W
Q = 500 VAr
Calcular las medidas de los amperímetros
An, Aa, Ab y Ac en el circuito de la figura. Se
sabe que es un sistema trifásico equilibrado de
tensiones con una tensión de línea (Uab) de
380 V.
P´ = 200 W
cos ϕ´ = 0.5 cap
n
An
CALIFICACIÓN:
DURACIÓN:
Todos los problemas tienen la misma puntuación. Es necesario obtener una calificación de 2 sobre 10
en cada uno de los problemas.
2 horas y 15 min