Ecuaciones ordinarias de la Parábola – Ejercicios Resueltos. x2

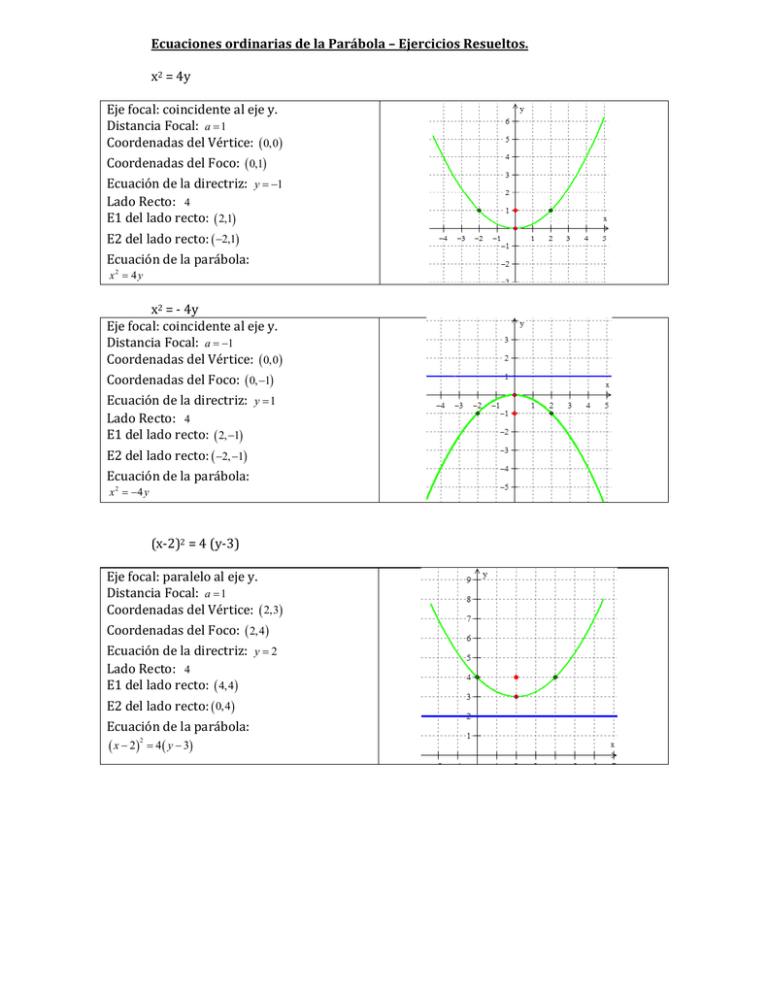
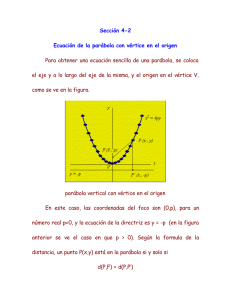
EcuacionesordinariasdelaParábola–EjerciciosResueltos.
x2=4y
Ejefocal:coincidentealejey.
DistanciaFocal: a  1 CoordenadasdelVértice:  0,0 CoordenadasdelFoco:  0,1 Ecuacióndeladirectriz: y  1 
LadoRecto: 4 E1delladorecto:  2,1 E2delladorecto:  2,1 Ecuacióndelaparábola:
x2  4 y x2=‐4y
Ejefocal:coincidentealejey.
DistanciaFocal: a  1 CoordenadasdelVértice:  0,0 CoordenadasdelFoco:  0, 1 Ecuacióndeladirectriz: y  1 
LadoRecto: 4 E1delladorecto:  2, 1 E2delladorecto:  2, 1 Ecuacióndelaparábola:
x 2  4 y (x‐2)2=4(y‐3)
Ejefocal:paraleloalejey.
DistanciaFocal: a  1 CoordenadasdelVértice:  2,3 CoordenadasdelFoco:  2,4 Ecuacióndeladirectriz: y  2 
LadoRecto: 4 E1delladorecto:  4,4 E2delladorecto:  0,4 Ecuacióndelaparábola:
2
 x  2   4  y  3 y2=8x
Ejefocal:coincidenteconelejex.
DistanciaFocal: a  2 CoordenadasdelVértice:  0,0 CoordenadasdelFoco:  2,0 Ecuacióndeladirectriz: x  2 
LadoRecto: 8 E1delladorecto:  2,4 E2delladorecto:  2, 4 Ecuacióndelaparábola:
y2  8x