practica 1. propiedades físicas de los fluidos

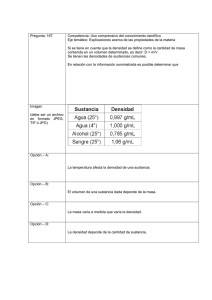
LABORATORIO DE TERMICA Y FLUIDOS
DEPARTAMENTO DE INGENIERÍA MECÁNICA
Práctica 1
PRESENTACION
EXÁMEN RÁPIDO
FORMATO
CALCULOS
RESULTADOS
DISCUSION DE
RESULTADOS
CONCLUSIONES
Mecánica de Fluidos
Propiedades Físicas
NOMBRE
MATRICULA
PROFESOR
INSTRUCTOR
TOTAL
5%
10%
10%
20%
20%
15%
20%
100%
Introducción
Para poder entender conceptos de la estática y dinámica de los fluidos es necesario
conocer algunas propiedades de éstos. En especial, las propiedades físicas del fluido nos
ayudan a estudiar su comportamiento como un continuo. En esta práctica se estudiarán las
propiedades físicas de una sustancia como son: densidad, peso específico, gravedad
específica y viscosidad.
Objetivos
 Conocer y utilizar los aparatos empleados para medir densidad, peso específico, gravedad
específica y viscosidad, y emplearlos para medir estas propiedades.
 Familiarizarse con diversas unidades utilizadas para medir estas propiedades.
Teoría
A. Definiciones de las propiedades físicas de los fluidos:
1.- Densidad absoluta (). Es la cantidad de masa contenida por unidad de volumen. En el
Sistema Internacional (SI) la densidad se mide en kg/m3, gr/cm3 o slug/ft3.
Donde:
 = densidad [=] M/L3
M = masa [=] M
V = volumen [=] L3
  M/V
2.- Densidad relativa (r). Se define como la relación que existe entre la densidad absoluta de
una sustancia y la de una sustancia de referencia. En el caso de los líquidos la sustancia de
referencia es el agua a una temperatura de 4C y una presión atmosférica (cercano a las
condiciones estándar); tratándose de los gases, generalmente se adopta el aire o el hidrógeno a
condiciones estándar.
r = sustancia / sust. referencia ; r = densidad relativa, adimensional.
3.- Peso específico (). Es el peso del fluido por unidad de volumen. Las unidades en el SI son
N/m3, o sea kg m/(s2m3).
Peso m  g
 

 g
V
V
Donde:
 = peso específico [=] M/(L2T2); Peso [=] ML/T2
V = volumen [=] L3; m = masa [=] M
g = 9.81 m/s2;  = densidad [=] M/L3
1
LABORATORIO DE TERMICA Y FLUIDOS
DEPARTAMENTO DE INGENIERÍA MECÁNICA
4.- Peso específico relativo (r). Se define como la relación que existe entre el peso específico
de una sustancia y el de una sustancia de referencia. Para la selección de las sustancias de
referencia se emplean las mismas que se mencionaron en la definición de densidad relativa.
r = sustancia / sust. referencia ; r = peso específico adimensional
El término gravedad específica (SG) se emplea para referenciar a la densidad relativa
o al peso específico relativo. Nótese que tienen el mismo valor numérico, esto es:
SG = sustancia / sust. referencia = sustancia / sust. referencia
Un fluido es una sustancia que sufre deformación continua cuando se sujeta a un
esfuerzo cortante. La resistencia a la deformación ofrecida por los fluidos recibe el nombre de
viscosidad dinámica o absoluta, la cual se define mediante la ley de Newton (la viscosidad
indica la facilidad con que un fluido fluye cuando actúan fuerzas externas sobre él).
 
du
dy
Donde:
 = esfuerzo cortante [=] F/L2
 = viscosidad dinámica del fluido [=] FT/L2 o M/LT
du/dy = gradiente de velocidad [=] T-1
u = velocidad [=] L/T
y = distancia [=] L
Figura 1. Fluido sometido a un movimiento cortante.
La unidad de viscosidad dinámica en el SI es el N s/m2. En el sistema inglés se utiliza
lbf-s/ft2. En el sistema CGS se utiliza el centipoise. Un poise equivale a 1 gr/(cm s), y 1
centipoise = 1cp = 0.01 poise.
En muchos problemas que involucran viscosidad, se debe relacionar la magnitud de las
fuerzas viscosas con la magnitud de las fuerzas de inercia, es decir, de las fuerzas que causan
la aceleración del fluido. Ya que las fuerzas viscosas son proporcionales a la viscosidad  y las
fuerzas de inercia a la densidad , frecuentemente se involucra esta relación, que es también
una propiedad de los fluidos llamada viscosidad cinemática, que se define por:



Donde:
 = viscosidad cinemática [=] L2/T
 = viscosidad dinámica del fluido [=] FT/L2 o M/LT
 = densidad [=] M/L3
En el SI la viscosidad cinemática se expresa en m2/s y en el sistema inglés en ft2/s. En
el sistema CGS es el stoke, que es igual a 1 cm2/s.
2
LABORATORIO DE TERMICA Y FLUIDOS
DEPARTAMENTO DE INGENIERÍA MECÁNICA
B. Instrumentos para medir las propiedades físicas de los fluidos:
1. Densímetro.
Instrumento que se utiliza para medir la densidad relativa de un fluido incompresible. Se
conforma por un tubo de vidrio delgado, el cual está graduado de manera ascendente de 0.650
a 1.000 en la parte inferior; esta escala se emplea para líquidos menos densos que el agua y
para líquidos pesados la escala va de 1.000 a 1.200. Su funcionamiento se basa en el principio
de Arquímedes, el cual establece que cuando un sólido se sumerge en un líquido sufre una
aparente pérdida de peso igual al peso del volumen del líquido desalojado.
Al establecer un equilibrio entre el peso y la fuerza debida al peso del líquido desalojado,
el cuerpo flota; por ello resulta que mientras menos denso sea el líquido en el que flota un
cuerpo, más se sumergirá.
Fuerzas
Boyantes
Figura 2. Densímetro
Utilizando el principio de Arquímedes para el caso del densímetro se obtiene:
Fy = 0 = FB - FW
FB = FW
f VD g = mD g
f At H = mD
f = mD/( At H)
Donde:
FB = fuerzas Boyantes [=] F
FW = fuerzas de gravedad (peso del densímetro) [=] F
f = densidad del fluido analizado [=] M/L3
VD = volumen desplazado [=] L3
mD = masa del densímetro [=] M
At = área transversal del bulbo [=] L2
g = aceleración de la gravedad = 9.81 m/seg2
H = altura de la parte sumergida del bulbo [=] L
Así pues, al introducirse un mismo densímetro en líquidos diferentes, variará el
volumen de la parte sumergida, y por lo tanto H. La densidad y la altura H son inversamente
proporcionales, esto es que mientras una aumenta su valor la otra disminuye, precisamente es
por esto que se puede poner una escala sobre el densímetro que indique directamente el valor
de la densidad del líquido analizado.
3
LABORATORIO DE TERMICA Y FLUIDOS
DEPARTAMENTO DE INGENIERÍA MECÁNICA
2. Medición de Peso Específico.
Para conocer el valor del peso específico se requiere un recipiente de volumen y peso
conocidos, llamado picnómetro. Este recipiente tiene una característica especial en su tapa, la
cual tiene un orificio de alivio de manera que el fluido excedente salga, garantizando así que
en todas las pruebas vamos a tener el mismo volumen.
Figura 3. Picnómetro.
3. Viscosímetro de Ostwald:
El viscosímetro de Ostwald está clasificado entre los viscosímetros capilares y de
orificio. Estos consisten en un tubo capilar de diámetro conocido, por el cual se hace fluir el
líquido que se requiere analizar y por medio de la ecuación de Hagen Poiseuille se relaciona el
gasto con la viscosidad. Este dispositivo consiste en dos bulbos conectados por un capilar.
Figura 4. Viscosímetro de Ostwald.
Su modo de operar consiste en situar el instrumento en posición vertical, se coloca en
el mismo un volumen fijo de líquido que se aspira hacia arriba hasta el bulbo superior A. Se
permite entonces al líquido fluir de retorno y se mide el tiempo que transcurre ente el paso de
nivel por las marcas M1 y M2. El viscosímetro con el que se cuenta en el laboratorio ya está
calibrado para determinar la viscosidad cinemática como una simple multiplicación de una
constante por el tiempo que tarda en pasar de la marca M1 a M2.
=C t
4
LABORATORIO DE TERMICA Y FLUIDOS
DEPARTAMENTO DE INGENIERÍA MECÁNICA
Pero esta constante no es un simple factor para que del resultado adecuado, sino que
viene de hacer un análisis de fuerzas en el tramo comprendido entre la marca M1 y la marca
M2, para ello se parte de la ecuación de Bernoulli:
Reduciendo términos
P V 2 (L / D)f


2
Como el régimen de flujo es completamente laminar, podemos determinar el factor de fricción
que es igual a 64/Re.
  g  h 1 2  4L  16 
 V   

2  D  Re 
g  h
 4L   
 4L   
  V  2  
 V 2  
8
 D  VD 
 D   
2
2
 g  h  D  t 
 g  h  D  1 

     




 8  4L  L 
 8  4L  V 
  Ct
Equipo
- Picnómetro
- Viscosímetro de Ostwald
- Densímetro
2
 g  h  D 

C

 8  4L  L 
Donde:
 = viscosidad cinemática [=] L2/T
C = constante del viscosímetro [=] L2/T2
t = tiempo [=] T
 = densidad [=] M/L3
- Termómetro 0 - 100C
- Vaso de precipitado
- Probeta graduada
- Báscula
- Cronómetro
- Sustancias problema
Bibliografía
[1] Manual del Laboratorio de Térmica y Fluidos, ITESM, 1999.
[2] Marks, Lionel S. et. al.; Manual del Ingeniero Mecánico; McGraw-Hill; 1996
[3] Mott, Robert L. Mecánica de Fluidos Aplicada; 4ª edición; Prentice Hall; 1996.
[4] Perry, John Howard, et. al.; Manual del Ingeniero Químico; McGraw-Hill; 1982
[5] White, Frank M. Fluid Mechanics; 3rd Edition, Mc Graw – Hill; 1994
5
LABORATORIO DE TERMICA Y FLUIDOS
DEPARTAMENTO DE INGENIERÍA MECÁNICA
Mecánica de Fluidos
Propiedades Físicas de los Fluidos
Fecha: ____________
Equipo: ____________
Nombre:______________________
Grupo:_______________
Matrícula:_____________
A) Procedimiento y Datos Experimentales
1.- Registre las temperaturas, con el termómetro de mercurio, de todas las sustancias que le
proporcione su instructor.
Sustancia
Agua
Alcohol
Glicerina
Aceite
Temperatura [C]
2.- Obtenga las densidades relativas, coloque la primera sustancia en la probeta y
posteriormente introduzca el densímetro, espere hasta que se equilibre y tome la lectura. Haga
el mismo procedimiento con las demás sustancias.
Sustancia
Agua
Alcohol
Glicerina
Aceite
Gravedad Específica
3.- Determine el peso específico de las sustancias con la siguiente metodología.
a) Pesar el recipiente vacío.
b) Registrar el volumen del recipiente.
c) Pesar el recipiente lleno de la sustancia problema.
d) Evaluar el peso de la sustancia obteniendo una diferencia de los valores
e) Dividir el valor del peso de la sustancia, generado en el inciso d, entre el volumen del
recipiente y se obtiene el valor del peso específico ().
I. Peso del picnómetro vacío y seco [g]: ___________________
II. Volumen del picnómetro vacío y seco [cm3]: ____________
Sustancia
Agua
Alcohol
Glicerina
Aceite
Peso del picnómetro con la sustancia [g]
6
LABORATORIO DE TERMICA Y FLUIDOS
DEPARTAMENTO DE INGENIERÍA MECÁNICA
4.- Para conocer la viscosidad siga el procedimiento que a continuación se muestra:
a) Lea en el instructivo del viscosímetro el valor de la constante C: _____________
b) Llene el viscosímetro con la muestra hasta la mitad del bulbo inferior (bulbo C). Es muy
importante que siempre lo llene hasta ese nivel para que los resultados sean
confiables.
c) Con la cantidad de líquido especificada en el inciso anterior, lleve el nivel del fluido
hasta que cubra el bulbo A.
d) Deje que el líquido se precipite y registre el tiempo que el nivel superior tarda en pasar
entre las dos marcas (de M1 a M2). Repita el mismo procedimiento con las demás
sustancias.
Sustancia
Tiempo [s]
Agua
Alcohol
Aceite
B) Resultados
1. Densidad de las sustancias:
slug/ft3
Sustancia
Agua
Alcohol
Glicerina
Aceite
kg/m3
g/cm3
kg/m3 (software)
2. Peso específico:
Sustancia
Agua
Alcohol
Glicerina
Aceite
lbf/ft3
kgf/m3
N/m3
3. Viscosidad cinemática:
Sustancia
Agua
Alcohol
Aceite
ft2/s
m2/s
stokes
centistokes
m2/s (software)
4. Viscosidad dinámica:
Sustancia
Agua
Alcohol
Aceite
lbf-s/ft2
N-s/m2
poise
7
centipoise
N-s/m2 (software)
LABORATORIO DE TERMICA Y FLUIDOS
DEPARTAMENTO DE INGENIERÍA MECÁNICA
Conclusiones:
1.- Calcula el porcentaje de error obtenido experimentalmente en el laboratorio comparando
contra los datos obtenidos con el software del texto, para cada líquido.
a) % Error en Densidad = (Dens. Exp – Dens. Real)/Dens. Real
 Agua ____________ %
 Alcohol ___________%
 Gasolina __________%
 Aceite ____________%
b) % Error en Viscosidad = (Visc. Exp – Visc. Real)/Visc. Real
 Agua ____________%
 Alcohol ___________%
 Aceite ____________%
2.- Formula conclusiones en base al error obtenido en cada líquido.
8