Contraste de hipótesis

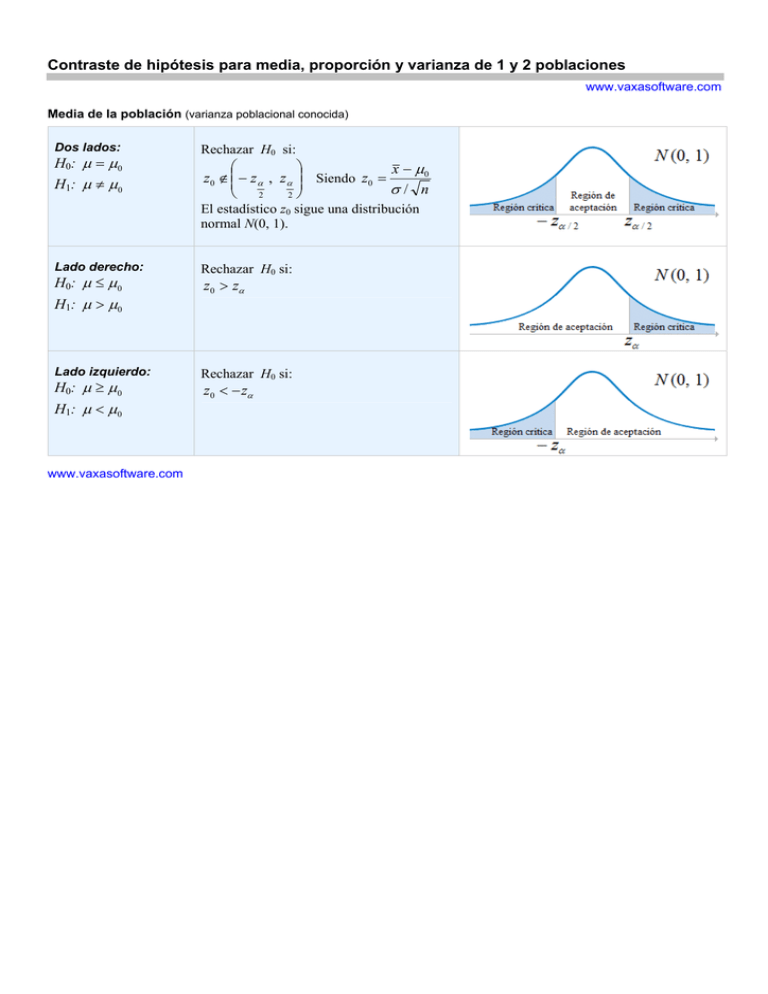
Contraste de hipótesis para media, proporción y varianza de 1 y 2 poblaciones
www.vaxasoftware.com
Media de la población (varianza poblacional conocida)
Dos lados:
H0: µ = µ0
H1: µ ≠ µ0
Rechazar H0 si:
⎛
⎞
x − µ0
z0 ∉ ⎜⎜ − zα , zα ⎟⎟ Siendo z0 =
σ/ n
2 ⎠
⎝ 2
El estadístico z0 sigue una distribución
normal N(0, 1).
Lado derecho:
H0: µ ≤ µ0
H1: µ > µ0
Lado izquierdo:
H0: µ ≥ µ0
H1: µ < µ0
www.vaxasoftware.com
Rechazar H0 si:
z0 > zα
Rechazar H0 si:
z0 < − zα
Media de la población (varianza poblacional desconocida)
Dos lados:
H0: µ = µ0
H1: µ ≠ µ0
Rechazar H0 si:
⎛
⎞
t0 ∉ ⎜ − t ⎛ α ⎞ , t ⎛ α ⎞ ⎟
⎜ ⎜ , n −1⎟ ⎜ , n −1⎟ ⎟
⎝ ⎝2 ⎠ ⎝2 ⎠⎠
x − µ0
Siendo t0 =
S/ n
El estadístico t0 sigue una distribución
t-Student de n-1 grados de libertad.
Lado derecho:
H0: µ ≤ µ0
H1: µ > µ0
Lado izquierdo:
H0: µ ≥ µ0
H1: µ < µ0
www.vaxasoftware.com
Rechazar H0 si:
t0 > t (α , n −1)
Rechazar H0 si:
t0 < −t (α , n −1)
Varianza de la población
Rechazar H0 si:
Dos lados:
H0: σ = σ
2
0
H1: σ ≠ σ
2
0
2
2
⎛
⎜
⎝
⎞
⎟
α
⎞
⎜ 1 − , n −1 ⎟
⎜ , n −1 ⎟ ⎟
2
⎝
⎠
⎝2
⎠⎠
2
(n − 1) S
Siendo χ 02 =
2
χ 02 ∉ ⎜ χ ⎛2
, χ ⎛2α
⎞
σ0
El estadístico χ sigue una distribución
Ji-cuadrado de n-1 grados de libertad.
2
0
Lado derecho:
H0: σ ≤ σ
2
2
0
H1: σ 2 > σ 02
Lado izquierdo:
H0: σ ≥ σ
2
2
0
H1: σ 2 < σ 02
www.vaxasoftware.com
Rechazar H0 si:
χ 02 > χ (2α , n −1)
Rechazar H0 si:
χ 02 < χ (21 − α , n −1)
Proporción de la población
Dos lados:
H0: p = p0
H1: p ≠ p0
Rechazar H0 si:
⎛
⎞
z0 ∉ ⎜⎜ − zα , zα ⎟⎟
2 ⎠
⎝ 2
n pˆ − n p0
Siendo z0 =
n p0 (1 − p0 )
El estadístico z0 sigue una distribución
normal N(0, 1).
Lado derecho:
H0: p ≤ p0
H1: p > p0
Lado izquierdo:
H0: p ≥ p0
H1: p < p0
Rechazar H0 si:
z0 > zα
Rechazar H0 si:
z0 < − zα
Diferencia de las medias de dos poblaciónes (varianzas poblacionales conocidas y distintas)
Dos lados:
Rechazar H0 si:
( σ 12 ≠ σ 22 )
⎞
⎛
z0 ∉ ⎜⎜ − zα , zα ⎟⎟
2 ⎠
⎝ 2
x − x2 − ∆ 0
Siendo z0 = 1
H0: µ1 − µ2 = ∆ 0
H1: µ1 − µ 2 ≠ ∆ 0
σ 12
n1
+
σ 22
n2
El estadístico z0 sigue una distribución
normal N(0, 1).
Lado derecho:
H0: µ1 − µ 2 ≤ ∆ 0
H1: µ1 − µ 2 > ∆ 0
Lado izquierdo:
H0: µ1 − µ 2 ≥ ∆ 0
H1: µ1 − µ 2 < ∆ 0
Rechazar H0 si:
z0 > zα
Rechazar H0 si:
z0 < − zα
Diferencia de las medias de dos poblaciones (varianzas poblacionales desconocidas e iguales)
Dos lados:
Rechazar H0 si:
( σ 12 = σ 22 )
⎛
⎞
⎟
t0 ∉ ⎜ − t ⎛ α
,
t
⎜ ⎜ , n 1 + n 2 −2 ⎞⎟ ⎛⎜ α , n 1 +n 2 −2 ⎞⎟ ⎟
⎠
⎝2
⎠⎠
⎝ ⎝2
x1 − x2 − ∆ 0
Siendo t0 =
1 1
+
SP
n1 n2
H0: µ1 − µ2 = ∆ 0
H1: µ1 − µ 2 ≠ ∆ 0
S P2 =
(n1 − 1) S12 + (n2 − 1) S 22
n1 + n2 − 2
El estadístico t0 sigue una distribución
t-Student de n1+n2–2 grados de libertad.
Lado derecho:
H0: µ1 − µ 2 ≤ ∆ 0
H1: µ1 − µ 2 > ∆ 0
Lado izquierdo:
H0: µ1 − µ 2 ≥ ∆ 0
H1: µ1 − µ 2 < ∆ 0
www.vaxasoftware.com
Rechazar H0 si:
t0 > t (α , n 1 +n 2 −2 )
Rechazar H0 si:
t0 < −t (α , n 1 +n 2 −2 )
Diferencia de las medias de dos poblaciones (varianzas poblacionales desconocidas y distintas)
Dos lados:
Rechazar H0 si:
( σ 12 ≠ σ 22 )
⎛
⎞
t0 ∉ ⎜ − t ⎛ α ⎞ , t ⎛ α ⎞ ⎟
⎜ ⎜ , ν ⎟ ⎜ ,ν ⎟ ⎟
⎝ ⎝2 ⎠ ⎝2 ⎠⎠
x − x2 − ∆ 0
Siendo t0 = 1
S12 S 22
+
n1 n2
H0: µ1 − µ2 = ∆ 0
H1: µ1 − µ 2 ≠ ∆ 0
ν=
(S
2
1
/ n1 + S 22 / n2 )
2
/ n1 ) (S 22 / n2 )
+
n1 − 1
n2 − 1
(S
2
1
2
2
El estadístico t0 sigue una distribución
t-Student de ν grados de libertad.
Lado derecho:
H0: µ1 − µ 2 ≤ ∆ 0
H1: µ1 − µ 2 > ∆ 0
Lado izquierdo:
H0: µ1 − µ 2 ≥ ∆ 0
H1: µ1 − µ 2 < ∆ 0
www.vaxasoftware.com
Rechazar H0 si:
t0 > t (α ,ν )
Rechazar H0 si:
t0 < −t (α ,ν )
Cociente de las varianzas de dos poblaciones
Rechazar H0 si:
Dos lados:
H0: σ = σ
H1: σ ≠ σ
2
1
2
1
2
2
2
2
⎛
⎞
⎟
F0 ∉ ⎜ F⎛ α
,
F
⎜ ⎜ 1 − , n 1 −1, n 2 −1⎞⎟ ⎛⎜ α , n 1 −1, n 2 −1⎞⎟ ⎟
⎠
⎝2
⎠⎠
⎝ ⎝ 2
2
S
Siendo F0 = 12
S2
El estadístico F0 sigue una distribución
F-Snedecor con n1-1 y n2-1 grados de
libertad.
Lado derecho:
H0: σ 12 ≤ σ 22
H1: σ 12 > σ 22
Lado izquierdo:
H0: σ ≥ σ
2
0
H1: σ < σ
2
0
2
2
www.vaxasoftware.com
Rechazar H0 si:
F0 > F(α , n 1 −1, n 2 −1)
Rechazar H0 si:
F0 < F(1 − α , n 1 −1, n 2 −1)
Diferencia de las proporciones de dos poblaciones
Dos lados:
H0: p1 = p2
H1: p1 ≠ p2
Rechazar H0 si:
⎛
⎞
z0 ∉ ⎜⎜ − zα , zα ⎟⎟
2 ⎠
⎝ 2
Siendo z0 =
pˆ =
pˆ1 − pˆ 2
⎛1 1⎞
pˆ (1 − pˆ ) ⎜⎜ + ⎟⎟
⎝ n1 n2 ⎠
n1 pˆ1 + n2 pˆ 2
n1 + n2
El estadístico z0 sigue una distribución
normal N(0, 1).
Lado derecho:
H0: p1 ≤ p2
H1: p1 > p2
Lado izquierdo:
H0: p1 ≥ p2
H1: p1 < p2
www.vaxasoftware.com
Rechazar H0 si:
z0 > zα
Rechazar H0 si:
z0 < − zα
Siendo:
1 − α Nivel de confianza
α
H0
H1
µ
x
Nivel de significación
Hipótesis nula
Hipótesis alternativa
Media poblacional
Media muestral
σ Desviación típica poblacional
S Desviación típica muestral
p Proporción de la población
p̂ Proporción de la muestra
n Tamaño de la muestra
z0 Estadístico del contraste que sigue una distribución normal de Gauss
t0 Estadístico del contraste que sigue una distribución t-Student de Gosset
F0 Estadístico del contraste que sigue una distribución F de Fisher-Snedecor
χ 02
Estadístico del contraste que sigue una distribución ji-cuadrado de Pearson
zα Punto porcentual de la distribución normal de Gauss con probabilidad superior α
t (α ,ν ) Punto porcentual de la distribución t-Student de Gosset con probabilidad superior α
con ν grados de libertad
Punto porcentual de la distribución ji-cuadrado χ de Pearson con probabilidad superior
α y con ν grados de libertad
F (α , ν1 , ν 2 ) Punto porcentual de la distribución F de Fisher-Snedecor con probabilidad superior α
y con grados de libertad ν 1 y ν 2
χ (2α ,ν )
www.vaxasoftware.com
2