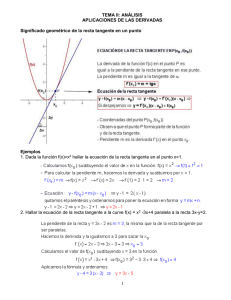
EXTREMOS y CURVATURA-INFLEXIÓN, una debajo de la otra. Así
Anuncio

EXTREMOS y CURVATURA-INFLEXIÓN, una debajo de la otra. Así se facilitará el estudio de todo ello y se detectarán posibles errores habidos en los cálculos. OBSERVACIONES: 1ª) Puede haber puntos en una función que sean a la vez extremos locales y puntos de inflexión. Lo que pasa es que en ellos la función no será derivable. Ejemplos: Ver los dibujos de la página 6. 2ª) Los puntos de tangencia vertical son siempre puntos de inflexión, aunque en ellos f no sea derivable. EJERCICIOS: 1. Estudiar la curvatura y puntos de inflexión aplicando el criterio de la derivada tercera a las funciones: y=2x3+4x2 , y=3x4-18x2 , f(x)=xex , g(x)=xlnx . 2. Dada la parábola y=ax2+bx+c , ¿en qué nos basaremos para saber, a primera vista, si es cóncava o es convexa? Dedúcelo razonadamente. 3. Estudiar la monotonía, extremos relativos, curvatura y puntos de inflexión de las funciones: a) y=3x 5-20x3 ; b) y=x4+8x3+22x2+24x+9 ; c) y=x3/(x-2)2 ; d) y=ex/x ; e) y=xlnx ; f) y=(1/2)sen2x+senx ; g) y=ln(x2+1) ; h) y=ln(x2-1) ; i) y=(x2-2x)(1/2) ; j) y=senx+cosx . 3.4. APLICACIÓN A LA LOCALIZACIÓN Y CLASIFICACIÓN DE LOS PUNTOS CRÍTICOS O SINGULARES DE UNA FUNCIÓN DEFINICIÓN: Los puntos de una función donde se anula su primera derivada se llaman puntos críticos o singulares. Por lo tanto, sus abcisas se hallan resolviendo la ecuación f ´(x)=0. Son puntos de tangencia horizontal (la pendiente de la recta tangente a la curva en ellos es cero). Sólo pueden tener puntos críticos las funciones que sean derivables, o más exactamente, las que tengan primera derivada y en puntos donde la tengan y sea nula. CLASIFICACIÓN: Estos puntos, o son máximos relativos o mínimos relativos o puntos de inflexión, pues la tangente, o deja la curva a un mismo lado antes y después de ellos, o la atraviesa. * Si x=a es uno de esos puntos (es decir, f ´(a)=0), la forma más práctica de clasificarlo es estudiar el signo de f ´un poco antes y un poco después: Si justo antes f ´es >0 y justo después f ´es <0 Þ en x=a habrá un máximo local Si justo antes f ´es <0 y justo después f ´es >0 Þ en x=a habrá un mínimo local Si f ´mantiene el signo un poquito antes y un poquito después Þ en x=a habrá punto de inflexión * Otra manera más formal, y siempre que existan las derivadas sucesivas en x=a, sería la basada en la FÓRMULA o TEOREMA DE TAYLOR: Si la primera derivada que no se anula en x=a fuese de orden par, entonces, si fuese > 0, habrá mínimo relativo, y si fuese < 0, máximo relativo. Mientras que si fuese de orden impar, habrá punto de inflexión; si fuese > 0 , la curva pasaría en él de cóncava a convexa, y al contrario si fuese < 0. EJERCICIO: Véase todo esto para f(x)=3x5-5x3 , g(x)=x3/(x-2)2 , h(x)=(x2-4)(1/2) , j(x)=1-(2-x)5. TEOREMA: Todo extremo relativo resultante de f ´(x)=0 es punto crítico. Lo contrario no tiene porqué ser cierto: no todo punto crítico tiene que ser extremo relativo (puede ser punto de inflexión). 3.5. APLICACIÓN AL ESTUDIO DE LOS EXTREMOS (MÁXIMOS Y MÍNIMOS) ABSOLUTOS DE UNA FUNCIÓN El teorema de Weierstrass ("toda función continua en un intervalo cerrado alcanza un máximo y un mínimo absolutos en él") nos da las condiciones para la existencia de un máximo o mínimo absolutos de una función en un intervalo, que, por otra parte, debe ser cerrado: si fuese abierto o semicerrado, no habría garantía de su existencia. Y ahora que hemos estudiado las derivadas, estamos en condiciones de hallarlos. Los extremos absolutos en el intervalo cerrado, o los alcanza en el abierto correspondiente, o en los extermos. Si lo hace en el abierto, son también relativos. Por lo tanto, habremos de seguir el siguiente procedimiento: 1º) Calculamos los extremos relativos que estén en el abierto, hallando en ellos el valor de la función (siempre con la precaucíón, como ya sabemos, de analizar también para ello los puntos en los que la función, siendo continua, no sea derivable, pues recordemos que pueden ser extremos locales) 2º) Calculamos los valores de la función en los extremos del intervalo. 8 3º) Comparamos todos los valores hallados (son ordenadas, f(x)): el mayor de todos corresponderá al máximo absoluto, y el menor, al mínimo absoluto, que se alcanzarán en sus respectivas x. Si no se cumpliera alguna de las hipótesis del teorema de Weierstrass, no querrá decir que no se cumpla la tesis, sino que no se podría asegurar que se cumpliera. Si aún así se desease estudiar la existencia de los extremos absolutos, habría que recurrir a otros medios, como, por ejemplo, representar la función en el intervalo, o estudiar sus discontinuidades en él, si tiene asíntotas verticales, etc. Lo mismo diremos si lo que se pretende es estudiar la existencia y localización de los extremos absolutos en todo el dominio de definición de la función. EJERCICIO: Estudia los extremos absolutos: a) De la función y=2x3-9x2+12x-3 en los intervalos [0 , 2] , [0 , 3] y en todo su dominio. b) De y=4x/(x2+4) en [-2 , 1] y en todo su dominio. c) De y=x2-4x+2 en [0 , 4] . d) De y=1/(1+IxI) en su ) dominio. e) De y=(x2+1)/(x2-1) en é 2 , +¥ , en é- 3 / 3 , 3 / 3ù , en (-1 , 0] y en [0 , 3]. f) De y=senx.cosx en ë ë û [ 5p / 6 , 3p / 2] . 3.6. APLICACIÓN A PROBLEMAS DE OPTIMIZACIÓN Se trata de resolver problemas en los que hay que optimizar (maximizar o minimizar) una determinada función bajo ciertas condiciones que se exponen en el enunciado (minimizar costes, maximizar beneficios, etc.). Suele ser útil para su resolución hacer algún dibujo referencial, ordenar los datos esquemáticamente y seguir estos pasos: 1º) Localizar en el enunciado la función que hay que maximizar (hacer máxima) o minimizar (hacer mínima), que podemos llamar "función objetivo", la cual puede ser que dependa de una, dos o más variables. A nosotros nunca se nos presentarán dependientes de más de dos variables. 2º) Si dependiera de dos variables, en el enunciado se nos dará algún dato o clave para relacionarlas mediante una ecuación o fórmula. De esta ecuación podremos despejar una de las variables en función de la otra (la que menos complicación traiga luego para derivar) y sustituiremos su valor en la función a optimizar (función objetivo) obtenida en el paso anterior, quedando así dependiente de una sola variable. 3º) Se hallan los máximos y mínimos de dicha función, los cuales deben ser absolutos en un cierto intervalo de variabilidad de la variable tomada como independiente que habrá que tener en cuenta. 4º) Se interpretan los resultados obtenidos, rechazando aquellos que no tengan sentido a la luz del enunciado, llegando a la solución, la cual habrá que expresar correctamente, sin olvidar las unidades de medida si las hubiera. El inconveniente muchas veces de este tipo de problemas no reside tanto en saber derivar ni hallar los extremos de la función cuanto en determinar la propia función. Es decir, en el paso primero. Y esto es debido a que se necesitan usar, como ya habrás notado que ocurre en casi todo lo que llevas de Análisis, conocimientos previos que viste en cursos pasados, como, por ejemplo, las fórmulas trigonométricas, las de los perímetros y áreas de figuras planas y sus nombres (triángulos, rectángulos, cuadrados, trapecios, trapezoides, rombos, romboides, círculos, polígonos regulares, sectores circulares, ...); las de las superficies laterales, totales y volúmenes de cuerpos en el espacio y sus nombres (cilindros, conos, prismas, pirámides, esferas, cubos, hexaedros, paralelepípedos, ortoedros, ...) y de propiedades intrínsecas que poseen y que has ido viendo a lo largo de la ESO. No se trata tanto de hacer un alarde memorístico como de encontrar una especie de hilo lógico que te servirá para deducir rápidamente muchas de ellas (desarrollo plano de las figuras espaciales, etc.). CINCO EJEMPLOS INTERESANTES Y REALES QUE RESOLVEREMOS EN CLASE: 1. Un granjero decide dedicar parte del terreno a cultivar rosas con la idea de venderlas. Por circunstancias decide que ese parterre sea rectangular, y debe vallarlo para que los animales que tiene sueltos no estropeen el cultivo. Sólo dispone de 400 m de tela metálica para ello, y se pregunta qué dimensiones debe dar al parterre para que pueda cultivar el mayor número de rosales posible. ¿Podríamos ayudarle? 2. Por estudios estadísticos se ha determinado que la cantidad de refresco que tomaría un adulto en un aperitivo se ajusta a unos 33 cl, y por motivos técnicos de apilamiento, comodidad para consumo y venta, se decide que sean envasados mayormente en latas cilíndricas. ¿Qué dimensiones (radio de la base y altura) deberán tener estos envases para que los gastos en su fabricación sean los mínimos posibles (sin tener en cuenta la composición del 9 material empleado)? (NOTA: Una vez halladas las dimensiones idóneas, si quieres comprobarlas con la realidad, ten en cuenta que deben tener unas bases con determinada forma para que encajen en su almacenamiento unas con otras, y una cámara interna sin líquido para la expansión adecuada de los gases en disolución de, aproximadamente, 180 mm de altura sobre la altura del líquido, manteniendo el radio básico). 3. Un propietario quiere dedicar 10000 m2 de su finca a la cría de ovejas, y quiere disponerlo en forma rectangular. Necesita vallarlo para que no se le escape el ganado, pero quiere gastarse en ello la menor cantidad posible. Si la alambrada, incluidas las barras contenedoras y la mano de obra, le sale a razón de 10 € el metro, ¿cuánto se gastará? 4. Sabido es que un quilate en pedrería es la unidad de masa empleada universalmente para pesar las piedras preciosas y las perlas, y que equivale a 200 mg en el Sistema Métrico Decimal. Para valorar el precio de un diamante es importante fijarse en cuatro factores esenciales que influirán en él: el color, la pureza, su peso en quilates y el tallado, aparte de las fluctuaciones de su cotización en el mercado. Actualmente, el mayor diamante tallado del mundo es la “Estrella de África”, propiedad de la Corona Británica, que pesa 530´20 quilates, o lo que es lo mismo, 106´040 g. Podremos hacernos una muy vaga idea de su precio, sin contar antigüedad, historia, pureza, tallado, circunstancias relativas a su adquisición, etc. etc., teniendo en cuenta que, a fecha de hoy (6 diciembre del 2014), el quilate de un diamante normal está a 2419 €. En cuanto al factor peso, el precio de un diamante suele ser directamente proporcional al cuadrado de su peso. Con este último dato: a) Demostrar que si un diamante se quiere partir en dos, pierde valor, e indicar cuánto es la pérdida. b) ¿Qué partición será la que haga máxima esa depreciación? (NOTA: Si P 1 es el precio antes de la partición y P2 el de después, se llama “depreciación” a la cantidad D = P1 – P2 ). ¿Cuánto costaría cada parte si el "Estrella de África" se dividiera en dos partes iguales? ¿Cuál sería su depreciación? 5. En una fábrica de cajas de cartón, la producción se hace a partir de placas de cartón de 60 cm por 30 cm, de la que se construyen cajas ortoédricas abiertas y otras cerradas. Para las abiertas, se corta un cuadradito en cada esquina; ¿cuánto debe medir el lado de dicho cuadrado para que, de todas las cajas posibles, se fabriquen aquellas que tengan la mayor cabida? En las cerradas, se corta un cuadradito en cada extremo de uno de los lados menores, y en cada una de las dos esquinas opuestas debe recortarse un trozo idéntico de cartón de manera que, al doblar y plegar, quede la caja hecha y cerrada con una tapa justa sin dobleces ni rebordes. Contestar a la misma pregunta del apartados anterior. PROBLEMAS: 1. Queremos construir un depósito prismático recto, abierto, de base cuadrada, que tenga 500000 litros de capacidad y cuyas dimensiones sean tales que nos cueste lo menos posible pintarlo. 2. Se considera una ventana rectangular rematada en la parte superior con un triángulo equilátero. Sabiendo que el perímetro de la ventana es de 6´60 m, hallar sus dimensiones de manera que entre la máxima luz por ella. 3. Un jardinero quiere construir un parterre en forma de sector circular. Si dispone de 20 m de alambre para rodearlo, ¿qué radio debe tener para que la superficie sea máxima? 4. Halla el radio de la base y la altura de un cilindro inscrito en una esfera de radio R en cada caso: a) Sea de volumen máximo. b) Tenga área lateral máxima. 5. Demuestra que la suma de un número real positivo no nulo y su inverso es siempre mayor o igual que 2. 6. Queremos dividir una cuerda de 1 m en dos para formar con una de las partes un cuadrado, y una circunferencia con la otra , de manera que la suma de las áreas encerradas sea la máxima posible. ¿Cuánto debe medir cada parte para conseguir nuestro propósito? 3.7. APLICACIÓN AL CÁLCULO DE FUNCIONES CON CONDICIONES Se trata de un tipo de problemas recíproco a aquellos en los que se nos daba una función conocida y nos pedían estudiar su monotonía, extremos, curvatura, puntos de inflexión, etc. Aquí es al revés: se conocen algunos extremos, puntos de inflexión, y algún que otro detalle de ella, y se nos pide que hallemos de qué función se trata. EJERCICIOS: 1. Hallar una función polinómica de tercer grado de coeficiente líder 1, sabiendo que tiene un punto de derivada nula en el (1 , 1), que no es extremo relativo. 2. ¿Qué función polinómica de tercer grado tendrá un máximo en (0 , 0) y un punto de inflexión en (1 , -4)? 3. ¿Cuántas funciones de la forma y=ax4+bx2+c tienen un máximo en (0 , 4) y un punto de inflexión para x=1? Razónalo. 4. De una cúbica se sabe que su tangente en (1 , 1) es la recta y=-x+2, y que tiene un extremo en (0 , 2). ¿De qué función se trata? ¿El extremo dado es máximo o mínimo? ¿Tiene algún punto de inflexión? 10 3.8. APLICACIÓN AL ESBOZO Y REPRESENTACIÓN GRÁFICA DE FUNCIONES EN FORMA EXPLÍCITA INTRODUCCIÓN Desembocamos en la última de las aplicaciones del Cálculo Diferencial en este curso, en la que converge cuanto hemos ido viendo en Análisis Matemático desde que comenzamos, allá por Primero o Segundo de la ESO, con el concepto de función. Hemos ido viendo propiedades y operaciones con funciones, cálculo de dominios, para lo que necesitábamos resolver todo tipo de ecuaciones, inecuaciones y sistemas. Hemos representando las funciones más elementales, desde una recta a una parábola, en funciones polinómicas; desde una hipérbola, en las racionales, a irracionales simples; desde las exponenciales y logarítmicas más elementales a las trigonométricas más inmediatas, y aquellas que estaban formadas con distintos trozos de las ya citadas. Incluso hemos tenido que acudir a recursos no demostrados, como hallar el vértice de una parábola, o asíntotas antes de ver el cálculo conjunto de ellas. Y nos quedábamos siempre a las puertas de poder esbozar otras funciones polinómicas (cúbicas, cuárticas, ...), racionales, irracionales, exponenciales, logarítmicas y trigonométricas no tan elementales, más complicadas de representar con las herramientas que teníamos y, con mucho menos, a base de simples tablas de valores. Llegamos, por fin, al culmen de nuestras aspiraciones: poder esbozar o representar, de manera totalmente fiable, cualquier función "que nos echen" en forma explícita. Y es que todo era imposible sin el Cálculo Diferencial, sin las derivadas. Y para llegar a ellas, también hemos tenido que recorrer un camino histórico: desde el concepto de función, pasando por el de límite y continuidad, hasta desembocar en el de derivada. Poseemos ya , como el carpintero en su taller, una más que abundante colección de herramientas para usar ante multitud de problemas que eran irresolubles hasta ahora para nosotros, entre los cuales destacamos la representación de cualquier función explícitamente dada. Ya lo tenemos todo y aquí finalizaremos esta parte del Análisis Matemático llamada Cálculo Diferencial, e iniciaremos otra gran aventura en busca de poder calcular cualquier tipo de área plana, aunque esté limitada por curvas, por cualquier curva, quedando las fórmulas conocidas de áreas como casos particulares. ¡Demostraremos, por fin, las expresiones del área del círculo y de la elipse! que hemos usado, la primera, desde siempre, y que nos las hemos creído como ciertas. También se solucionará el poder hallar la longitud de cualquier tramo de curva, pudiéndose deducir la fórmula de la longitud de la circunferencia o la de la elipse, y se podrán calcular volúmenes de revolución generados por cualquier curva, aunque estos últimos problemas se abordarán ya en los primeros cursos de las carreras técnicas, por sobrepasar los objetivos marcados en Segundo de Bachillerato. Hacia todo esto nos llevará un nuevo camino que descubriremos al abrir una puertecita escondida e insignificante del Cálculo Diferencial. Ese camino se llama, dentro del Análisis, "Cálculo Integral". DESARROLLO DE ESTE PUNTO ¿Cuáles son las herramientas que tenemos para poder esbozar o representar funciones? Las enumeramos todas: Dominio, continuidad, derivabilidad, simetrías, periodicidad, asíntotas, ramas infinitas, corte con los ejes, puntos singulares, crecimiento, extremos relativos, curvatura, puntos de inflexión, regionamiento y tabla auxiliar de valores. Así como un carpintero no usa todas sus herramientas cada vez que hace un trabajo, así tampoco nosotros usaremos todas cada vez que tengamos que representar una función. Tan sólo las que necesitemos en cada caso, y cada caso puede ser diferente a otro. Generalmente usaremos las marcadas en negrita, de manera que podríamos seguir los siguientes pasos en la representación: 1. DOMINIO Y CONTINUIDAD. 2. DERIVABILIDAD (se calculan al menos las dos primeras derivadas) 3. SIMETRÍAS (se podrán usar convenientemente, si las hay, para ahorrar cálculos) 4. PERIODICIDAD (únicamente en caso de aparecer sólo funciones trigonométricas) 5. CORTE CON LOS EJES (a partir de aquí conviene ya, aparte, ir dibujando sobre los ejes lo que vayamos obteniendo) 6. ASÍNTOTAS Y RAMAS INFINITAS. 7. CRECIMIENTO Y EXTREMOS RELATIVOS (cuyo esquema se dibujará como se ha hecho en clase, de manera que se deje, justo debajo, espacio para dibujar paralelamente el esquema correspondiente a la 11 curvatura e inflexión, por si hubiera alguna conexión que nos permitiera ahorrar cálculos y tiempo, o descubrir algún fallo en cálculos anteriores) 8. CURVATURA E INFLEXIÓN. Si con estos pasos aún quedase algo no claro (cosa muy poco probable en donde nos vamos a mover), podemos recurrir a las demás herramientas. De todas ellas tenemos sobradas nociones dadas en estos dos cursos de Bachillerato. Sólo cabe añadir y recordar: a) Que las simetrías que usaremos serán sólo dos: respecto al eje OY, f(-x)=f(x) (si una función la posee diremos que es una función par) , y respecto al origen de coordenadas, f(-x)=-f(x) (función impar). b) Referente a la periodicidad, decir que sólo la manejaremos en funciones trigonométricas. Y que si f(x) tiene de periodo principal k, la función f(mx+n) tendrá de periodo k/m. Y si f(x) y g(x) son periódicas, las funciones f (x)± g(x) , f (x)× g(x) y f (x) / g(x) son periódicas, y sus periodos serán, como máximo, el mínimo común múltiplo de los periodos de f y g. c) A la hora de representar una función, conviene que hagas el estudio analítico siguiendo los pasos expuestos, y al acabar de dibujarla, debe encajar todo el estudio hecho, con el dibujo. EJERCICIO: Hallar los periodos de las funciones: y=sen(2x-1) ; y=tg(3x) ; y=senx + cosx ; y=(1/2)cos2x + senx ; y=(senx)/4 ; y=3senx-sen3x ; y=(cosx)/x ; y=senx . cosx ; y=sen2x ; y=tg(x/2 . NOS REMITIMOS YA A LOS EJERCICIOS Y EJEMPLOS QUE IREMOS HACIENDO EN CLASE Guillermo Molina Profesor de la asignatura 12