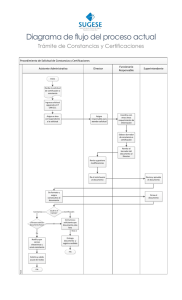
Document

Solución de ecuaciones no
lineales con una variable.
●
Definición del problema:El problema se puede
expresar de la siguiente manera: encontrar el
✳
*
valor de x tal que f  x =0. Cuando en f hay
términos no lineales la solución no es sencilla.
p. ej:
5
3
f  x=3x −x 7x−4
−x
4
f  x=e sin xln 5xx
5
3
3x −x 7x−4
f  x= 3 2
7x −x 4x1
✳
✳
Como encontramos los ceros? x : f  x =0
1
Solución de ecuaciones no lineales
con una variable.
●
Solución al problema. Existen varios métodos,
p.e:
–
–
–
–
●
Método de Bisección.
Método de Punto Fijo.
Método de Newton-Raphson.
Etc.
No hay un método general, dependiendo del
conocimiento que tengamos del problema
podemos elegir alguno de ellos.
2
Método de Bisección(sol.).
●
Solución al problema: El método se basa en el conocimiento
de dos puntos, los cuales sabemos que están entre una raíz
de la función a analizar:
En este caso x1 y x2 son los puntos necesarios para
encontrar la solución x1*; x2 y x3 para la solución x2*; x3 y x4
para la solución x3*
3
Método de Bisección
(Solución cont.).
●
Dados f(x) y los dos puntos de arranque, se
asume que la solución está justo al centro de
estos dos puntos.
x D x I
x m=
2
4
Método de Bisección
(Solución cont.).
●
Si la suposición es falsa:∣ f  x m ∣≥ f. Se revisa el signo
de f  x m  y se elige para ser sustituido el punto donde la
evaluación en f tenga el mismo signo. (de esta manera
se asegura tener a la solución entre xd y xi).
–
●
Se vuelve a calcular el punto medio y se repite el
paso anterior hasta convergencia.
Si la suposición es cierta:∣ f  x m ∣ f ,o se cumple algún
otro criterio de paro, se termina el programa.
5
Método de Bisección (Algoritmo.).
●
Se define el criterio de convergencia cc 1e-4
Se define el criterio de exactitud ce 1e-4
Se define el critero de itermax itmax 100000
Se declaran las variables fm,fi,fd,xi,xd,xm,xma;
Se declara it como entero
se asigna a it=0;
lee los valores de xi y xd;
asigna a xm=1e20;
repite:
asigna a xma=xm;
asigna a xm=(xi+xd)/2.0;
asigna a fi=f(xi);
asigna a fd=f(xd);
asigna a fm=f(xm);
si fi*fm>=0
asigna a xi=xm;
si no si fd*fm>0
asigna a xd=xm;
si no
imprime la solucion no está entre xi y xd;
asigna a it=itmax;
se asigna a it=it+1;
mientras que abs(fm)>ce y abs(xma-xm)>cc y it<itmax ;
imprime el valor de xm y el valor de fm;
fin del programa;
6
Método de Bisección.
●
Programa: Ver la tarea 6.
●
Verificación:
–
f  x= x−3 x2= x 2− x−6
Primera corrida: xi=-3, xd=-1.
Segunda corrida: xi=-1, xd=4.
–
3
2
f  x= x 2x 10x−20
corrida: xi=1, xd=2.
7
Método de Punto Fijo.
●
●
*
Definición del problema:encontrar el valor de x
✳
tal que f  x =0 .
Solución al problema: Transformar
algebraicamente:
f  x=0
g  x= x
Se logra despejando a una x de f(x)
8
Método de Punto Fijo.
●
Por ejemplo
2
f  x=2x −x−5=0
2
x=2x −5=g  x
x5
x=
=g  x
2
2
2x − x−5
x=x
=g  x
4x−1
5
x=
=g  x
2x−1

9
Método de Punto Fijo.
●
●
Una vez escrita la forma equivalente hay que
identificar un punto cercano a la raíz de interés,
se puede hacer por observación, graficando la
función, etc. A este punto se le llama punto de
arranque x0.
Con x0 se calcula x1 de la siguiente manera
x 1=g  x 0 
de forma general:
x i1=g  x i 
10
Método de Punto Fijo
(convergencia).
●
●
●
Si el valor de f  x≤ f ó ∣x i1−x i∣≤ x hemos
llegado a una solución.
Si no, iterar nuevamente los pasos anteriores.
Algunas veces la elección de g(x) hará que
consigamos llegar a la raíz, otras no, por que?.
x i1=g  x i 
x ✳= g  x ✳ 
✳
✳
x −x i1=g  x −g  x i 
11
Método de Punto Fijo
(convergencia).
●
Usando el teorema del Valor Medio, asumiendo
que en el intervalo [a,b] g es continua y
diferenciable en (a,b), entonces:
g b−g a
∃∈a , btal que g ' =
b−a
✳
g  x −g  x i 
g ' =
x ✳ −xi
✳
✳
g '  x −x i =g  x −g  x i 
✳
✳
g '  x −xi =x − x i1
✳
✳
∣x −x i1∣=∣g ' ∣∣x −x i∣
12
Método de Punto Fijo
(convergencia).
●
●
Note que el primer término es el EA en la
iteración i+1 y el término de la extrema derecha
es EA de la i-esima iteración. Entonces solo si
∣g '  x∣1 se consigue que el error vaya
disminuyendo.
Para asegurar convergencia es necesario
asegurar que para cada valor de x en el intervalo
(a,b) la derivada sea menor a 1.
13
Método de Punto Fijo (Algoritmo.).
●
Se define el criterio de convergencia cc 1e-4
Se define el criterio de exactitud ce 1e-4
Se define el criterio de itermax itmax 100000
Se declaran las variables x0,xi,xim1,fxi,fxim1;
Se declara it como entero
se asigna a it=0;
lee el valor de x0;
asigna a xi=x0;
asigna a fxi=f(x0);
repite:
asigna a xim1=xi;
asigna a fxim1=fxi;
asigna a xi=g(xim1);
asigna a fxi=f(xi);
asigna a it=it+1;
mientras que abs(fxi)>ce y abs(xi-xim1)>cc y it<itmax;
imprime el valor de xi y el valor de fxi;
fin del programa;
14
Método de Punto fijo.
●
Programa:
punto_fijo.c en:
http:\\www.ifug.ugto.mx\~gonzart\notas\punto_fijo.c
http:\\www.ifug.ugto.mx\~gonzart\notas\punto_fijo2.c
●
Verificación:
–
–
x6
f  x= x−3 x2= x − x−6=0 ; x=
=g  x
x
Punto de arranque: -3
Punto de arranque: 4
2
cos x−3x=0 ; x=cos x/3= g  x
Punto de arranque =1.2
15
Método de Newton-Raphson.
●
●
Definición del problema:encontrar el valor de x*
tal que f  x ✳ =0.
Solución al problema: aproximar f(x) con una
linea y ver donde la linea intersecta al eje x.
16
Método de Newton-Raphson.
●
La linea seleccionada es la tangente que pasa
por el punto xi. Y su intersección será en nuevo
valor de x, esto se repite hasta el criterio de paro.
–
Como se calcula el nuevo valor de x?.La recta tiene
la pendiente:
m= f '  x i 
17
Método de Newton-Raphson.
–
La recta tendrá la ecuación:
y− f  xi = f '  x i  x−x i 
–
La intersección con el eje x se da en y=0.
0− f  xi = f '  x i  x−x i 
f  xi 
x=x i −
f '  xi 
f  xi 
x i1= xi −
si f '  x i ≠0
f '  xi 
18
Método de Newton-Raphson.
●
●
En el método de Newton-Raphson necesitamos saber,
f(x), f'(x) y un punto de arranque.
Limitaciones: el algoritmo solo se aplica para funciones
que son derivables, el método fallará cuando xi se
localice en un mínimo o máximo.
19
Método de Newton-Raphson (Algoritmo).
●
Se define el criterio de convergencia cc 1e-4
Se define el criterio de exactitud ce 1e-4
Se define el criterio de itermax itmax 100000
Se declaran las variables x0,xi,xiM1,fxi,fxiM1,dfxi;
Se declara it como entero
se asigna a it=0;
lee el valor de x0;
asigna a xiM1=x0;
asigna a fxiM1=f(xiM1);
repite:
asigna a xi=xiM1;
asigna a fxi=fxiM1;
//evaluación de la derivada en el punto xi
asigna a dfxi=f'(xi);
asigna a xiM1=xi-fxi/dfxi;
//evaluación de la funcion f en el punto xiM1
asigna a fxiM1=f(xiM1);
asigna a it=it+1;
mientras que abs(fxiM1)>ce y abs(xi-xiM1)>cc y
it<itmax;
imprime el valor de xiM1 y el valor de fxiM1;
fin del programa;
20
Método de Newton-Raphson.
●
Programa: Ver la tarea 7.
●
Verificación:
–
–
f  x= x−3 x2= x 2− x−6=0 ; f '  x=2x−1
Punto de arranque: -3
Punto de arranque: 4
f  x=cos x−3x=0 ; f '  x=−sin  x−3
Punto de arranque =1.2
21
Puntos de Arranque
●
Como conseguir un “buen” punto de arranque?.
–
Si la función tiene algún significado físico, usar el
conocimiento del fenómeno.
–
Graficar la función f(x) y por observación elegir el
punto de arranque. Si no se tiene un graficador usar
las técnicas de calculo diferencial.
22