Cálculo de los Parámetros en el Método Logarítmico del

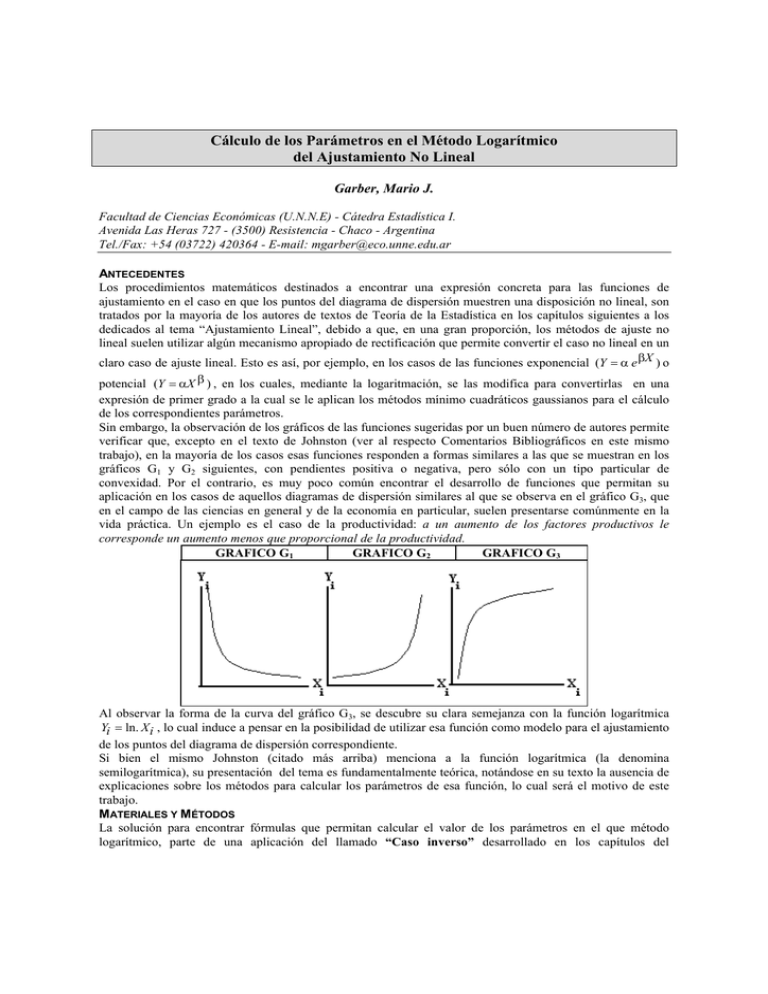
Cálculo de los Parámetros en el Método Logarítmico
del Ajustamiento No Lineal
Garber, Mario J.
Facultad de Ciencias Económicas (U.N.N.E) - Cátedra Estadística I.
Avenida Las Heras 727 - (3500) Resistencia - Chaco - Argentina
Tel./Fax: +54 (03722) 420364 - E-mail: [email protected]
ANTECEDENTES
Los procedimientos matemáticos destinados a encontrar una expresión concreta para las funciones de
ajustamiento en el caso en que los puntos del diagrama de dispersión muestren una disposición no lineal, son
tratados por la mayoría de los autores de textos de Teoría de la Estadística en los capítulos siguientes a los
dedicados al tema “Ajustamiento Lineal”, debido a que, en una gran proporción, los métodos de ajuste no
lineal suelen utilizar algún mecanismo apropiado de rectificación que permite convertir el caso no lineal en un
claro caso de ajuste lineal. Esto es así, por ejemplo, en los casos de las funciones exponencial (Y = α e βX ) o
potencial (Y = αX β ) , en los cuales, mediante la logaritmación, se las modifica para convertirlas en una
expresión de primer grado a la cual se le aplican los métodos mínimo cuadráticos gaussianos para el cálculo
de los correspondientes parámetros.
Sin embargo, la observación de los gráficos de las funciones sugeridas por un buen número de autores permite
verificar que, excepto en el texto de Johnston (ver al respecto Comentarios Bibliográficos en este mismo
trabajo), en la mayoría de los casos esas funciones responden a formas similares a las que se muestran en los
gráficos G1 y G2 siguientes, con pendientes positiva o negativa, pero sólo con un tipo particular de
convexidad. Por el contrario, es muy poco común encontrar el desarrollo de funciones que permitan su
aplicación en los casos de aquellos diagramas de dispersión similares al que se observa en el gráfico G3, que
en el campo de las ciencias en general y de la economía en particular, suelen presentarse comúnmente en la
vida práctica. Un ejemplo es el caso de la productividad: a un aumento de los factores productivos le
corresponde un aumento menos que proporcional de la productividad.
GRAFICO G1
GRAFICO G2
GRAFICO G3
Al observar la forma de la curva del gráfico G3, se descubre su clara semejanza con la función logarítmica
Yi = ln. X i , lo cual induce a pensar en la posibilidad de utilizar esa función como modelo para el ajustamiento
de los puntos del diagrama de dispersión correspondiente.
Si bien el mismo Johnston (citado más arriba) menciona a la función logarítmica (la denomina
semilogarítmica), su presentación del tema es fundamentalmente teórica, notándose en su texto la ausencia de
explicaciones sobre los métodos para calcular los parámetros de esa función, lo cual será el motivo de este
trabajo.
MATERIALES Y MÉTODOS
La solución para encontrar fórmulas que permitan calcular el valor de los parámetros en el que método
logarítmico, parte de una aplicación del llamado “Caso inverso” desarrollado en los capítulos del
Ajustamiento Lineal, en el que aparece la posibilidad, no de encontrar la recta de ajustamiento Y$i = a1 + b1 X i ,
sino la recta alternativa X$ i = a2 + b2Yi , inversa de la anterior, a la que denomino “recta reflejo” (nombre que
proviene de considerar que ambas son la misma recta observada desde ejes de referencia diferentes, por lo que
se podría considerar a la recta X$ i un “reflejo” de la recta Y$i ).
Por consiguiente la función logarítmica puede pensarse también como una función exponencial del
tipo X i = e Y , ya que si en esta última aplicamos logaritmos, obtendremos su inversa ln. X i = Yi ln. e = Yi
(recordando que ln.e=1).
A continuación, si construimos una función exponencial incluyendo en ella un par de parámetros γ y δ,
obtenemos la expresión X i = γ eδ Y , a la que llamaremos función exponencial completa. Siguiendo con el
procedimiento indicado en el párrafo anterior, para su rectificación aplicamos logaritmos y obtenemos
ln. X i = ln.γ + δYi ln. e = ln. γ + δYi .
Efectuamos un reemplazo apropiado de términos, haciendo
ln. X i = xi 

ln. γ = c 
(1)
δ =d


Yi = yi

obteniendo la ecuación de primer grado xi = c + dyi , en la cual es posible calcular los parámetros c y d
mediante las fórmulas generadas por el método de los mínimos cuadrados de Gauss. Es decir que
2
∑ xi ∑ yi − ∑ yi ∑ yi xi
y que
c=
n ∑ yi2 −(∑ yi )2
n ∑ yi xi − ∑ xi ∑ yi
.
d=
2
n ∑ yi2 −( ∑ yi )
Luego, se pueden obtener los valores de los parámetros γ y δ haciendo γ = anti ln. c y δ = d , con los cuales
se está en condiciones de construir la función logarítmica completa. Para ello, en la expresión xi = c + dyi , se
x −c
despeja la variable yi obteniéndose yi = i
. A partir de las transformaciones efectuadas anteriormente en
d
(1), esta última expresión resulta ser igual a
ln. X i − lnγ
Yi =
δ
que puede calcularse sin inconvenientes, ya que se conocen los valores de los parámetros γ y δ. El resultado
obtenido es una expresión funcional cuya gráfica sigue el movimiento logarítmico.
DISCUSIÓN DE RESULTADOS
Ejemplo: Una empresa posee sucursales de diferente tamaño. Al tomar datos respecto de la productividad en
esas sucursales, obtiene el siguiente cuadro.
Nº de
Productiempleados
vidad
xi =lnXi
xi yi
yi2
Y$
Xi
Yi =yi
10
10
2,30258
23,026
100
15,8
30
70
3,40119
238,083
4900
57,7
60
90
4,09434
368,491
8100
84,1
100
100
4,60517
460,517
10000
103,6
150
110
5,01063
551,169
12100
119,0
380
19,41391
1641,286
35200
a) Ajustar la productividad en función del número de empleados y
b) Estimar cuál sería la productividad en una sucursal con 50 empleados.
Solución: a) Los parámetros se calculan haciendo
(19,41391)( 35200) − (1641,286)( 380) = 1,888 ; d = 5(1641,286) − ( 380)(19,41391) = 0,2623
c=
5 35200 − 380 2
5 35200 − 380 2
(
) (
)
(
) (
)
⇒ γ = anti ln.1888
= 6,606 y δ = 0,02623 .
,
ln. X i − ln 6,606
Luego : Y$i =
0,02623
ln.50 − ln.6,606
b) Estimación para Xi=50: Y$ =
= 77,16
0,02623
GRAFICO
CONCLUSIONES
El procedimiento propuesto permite el cálculo de los parámetros en el modelo logarítmico del ajustamiento
lineal y su aplicación en casos prácticos concretos sin dificultades ni metodológicas ni empíricas.
BIBLIOGRAFÍA
1) Johnston - “Métodos de Econometría” - Editorial Vinces-Vives - Tercera Edición - 1975.
2) Kazmier y Díaz Mata – “Estadística Aplicada a Administración y Economía” – Editorial McGrawHill – Segunda Edición – 1990.
3) Gujarati - “Econometría” - Editorial McGraw-Hill - Segunda Edición - 1993.
4) Berenson y Levine – “Estadística Básica en Administración – Concepto y aplicaciones” Editorial
Prentice Hall – Sexta edición –1997.
5) Miller, Freund y Johnson – “Probabilidad y Estadística para Ingenieros” – Editorial Prentice Hall –
Cuarta Edición – 1995.
6) Mendenhall y Reinmuth – “Estadística para Administración y Economía” – Grupo Editorial
Iberoamérica – 1993.
7) Ang y Tang – “Probability Concepts in Engineering Planning and Design” – Volume I –Editorial
Wiley and Sons, Inc. Comentarios bibliográficos: En los cuadros siguientes se cita la bibliografía consultada indicando, para cada
texto, en qué capítulo, sección y página presenta el modelo propuesto y cuál es la expresión de la función
correspondiente, manteniendo la simbología y la nomenclatura utilizadas por cada autor.
Texto Nº 1)
Capítulo
Sección
3
3.1
Página
49
Modelo
Multiplicativo
3
3.1
52
3
3.1
53
3
3.1
54
Transformación
semilogarítmica (1)
Transformación
Y = AX β ; Y = AX −β
logarítmica doble (1)
Transformación inversa
β
β
Y =α+
; Y =α− ;
o recíproca
X
X
Fórmula de la función
t
Zt = AB vt
Y = α + β log X ; X = ABY
Texto Nº 2)
Capítulo
Sección
16
16.2
Página
315
Modelo
Exponencial
Texto Nº 3)
Capítulo
Sección
6
6.3
Página
151
Modelo
Log.Log.
6
6.3
154
Semilog.
Fórmula de la función
β2 ui
Y = β1 X i e
Y = β1 + β2 ln. X i + ui
6
6.3
157
Transformación
recíproca
Y = β1 + β2 
Y = b0b1
Fórmula de la función


1 



X i 
 ui
Texto Nº 4)
Capítulo
Sección
18
18.11
Página
806/7
Modelo
Polinomial
18
18.13
822
18
18.13
822
18
18.13
822
Transformación de raíz
cuadrada
Transformación
logarítmica
Transformación
recíproca
18
18.13
823
Exponencial
Y$i = eβ 0 + β1 X 1i + β 2 X 2i ε
Texto Nº 5)
Capítulo
Sección
11
11.3
Página
347
Modelo
Polinomial
Fórmula de la función
y = β 0 + β1x + β2 x 2 +...+ β p x p
11
11.3
347
Exponencial
11
11.3
349
Recíproco
y = αβ X
1
y=
α + βX
Texto Nº 6)
Capítulo
Sección
15
15.7
Página
503
Modelo
de crecimiento
(exponencial)
Yˆ = ae ε ′
Texto Nº 7)
Capítulo
Sección
7
7.3
Página
300
Modelo
Exponencial
Fórmula de la función
$
Y = β 0 + β1 X 1 + β 2 X 12 + ε
Y$ = β0 + β1 X 1i + β2 X 2i + ε
Y$ = β0 + β1 ln. X 1i + β2 ln. X 2i + ε
1
1
Y$ = β0 + β1
+ β2
+ε
X 1i
X 2i
Fórmula de la función
bx
Fórmula de la función
Y = αe
− βT
Notas: (1) Denominadas “Exponencial” y “Potencial”, respectivamente, por la mayoría de los autores.