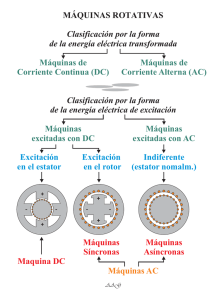
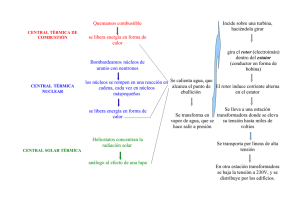
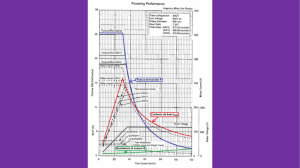
s - Cenidet
Anuncio

cnológico Subsecretaría de Educación Superior Dirección General de Educación Superior Tecnológica Coordinación Sectorial Académica Dirección de Estudios de Posgrado e Investigación Centro Nacional de Investigación y Desarrollo Tecnológico Subdirección Académica Departamento de Ingeniería Electrónica TESIS DE DOCTORADO EN CIENCIAS Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía presentada por M. C. Miguel Ángel Durán Fonseca como requisito para la obtención del grado de Doctor en Ciencias en Ingeniería Electrónica Director de tesis Dr. Gerardo Vicente Guerrero Ramírez Codirector de tesis Dr. Abraham Claudio Sánchez Cuernavaca, Morelos, México. Febrero de 2013. Dedicatoria A Dios A mi esposa e hijos A mis padres y hermanos Agradecimientos A mis asesores: Dr. Gerardo Vicente Guerrero Ramírez y Dr. Abraham Claudio Sánchez, por su tiempo y apoyo durante la realización de este trabajo de tesis. A mis revisores: Dr. Jorge Hugo Calleja Gjumlich, Dr. Manuel Adam Medina, Dr. Jesús Aguayo Alquicira, Dra. Ilse Cervantes Camacho, Dr. Ciro Alberto Núñez Gutiérrez, por sus valiosos comentarios que ayudaron a enriquecer este trabajo. A mis compañeros del grupo de trabajo de vehículos eléctricos: Iván Alcalá, Juan Aguilera, Saúl González†, Diego Langarica, Miguel Beltrán, Eunice Herrera y Gabriel Beltrán, por su aportación a este trabajo. A mis compañeros de Doctorado en Electrónica y Mecatrónica: Mario Juárez, Efrén Flores, Fermín Martínez, Armando Olmos, Héctor Romero, Iván Alcalá, Adriana Aguilera, Adriana Téllez, Tomas Higareda, Edwing Moreno, Cornelio Morales, JC Yris, Raúl Nava, Fabricio Escobar, Leobardo Hernández, Víctor Olivares, Rodolfo Vargas, Manuel Hernández, Antonio Aqui, Felipe Sorcia, Aurelio Brizuela, José Rodríguez, Julio Rodríguez, Alejandro Vázquez, Ronay López, Aldo Higuera, Raúl Jiménez, Cinda Sandoval, Marco Rodríguez, Ernesto Bárcenas, Freddy Chan y Albino Martínez, por su grata compañía durante mi estancia en el cenidet. Al personal docente del departamento de electrónica que contribuyó en mi formación académica, en especial a: Dr. Carlos Astorga y Dr. Carlos Daniel García. A mis compañeros de la Facultad de Ingeniería Electromecánica de la Universidad de Colima que siempre me brindaron su apoyo. A todo el personal del cenidet, en especial a: Ana Pérez, Maira Correa, Lorena Ruiz, Olivia Maquinay, Mario Moreno, Eduardo Velasco y Alfredo Terrazas. A la Universidad de Colima y al Promep por el apoyo económico brindado que me permitió desarrollar mis estudios de Doctorado. Resumen En un vehículo eléctrico se debe controlar el par generado por el motor, esto con el objetivo de imitar el funcionamiento de un vehículo con motor de combustión interna. Además, es importante cuidar el consumo de energía debido a que en un vehículo eléctrico se cuenta con una cantidad limitada de energía almacenada en las baterías. En esta tesis se presenta el diseño un controlador para el par y flujo magnético de un motor de inducción trifásico tipo jaula de ardilla, el cual impulsa un vehículo eléctrico alimentado por baterías. Adicionalmente, se desarrolla un algoritmo de selección de flujo magnético para reducir el consumo de energía durante el funcionamiento del vehículo. Para el diseño del controlador del vehículo y posteriormente examinar su desempeño se necesita un modelo matemático del vehículo eléctrico. Este se obtiene a partir del análisis del funcionamiento individual de sus componentes y la interacción de estos durante el funcionamiento del vehículo. El diseño del controlador parte del principio de producción del par y el modelo matemático del motor de inducción. Del análisis del control directo de par se deduce que el par electromagnético desarrollado por el motor de inducción puede controlarse por medio del flujo magnético del estator. Para controlar el flujo magnético del estator, y a su vez el par, se actúa sobre el voltaje trifásico aplicado al estator del motor de inducción. El algoritmo de selección de flujo tiene el objetivo de disminuir las pérdidas eléctricas que se presentan. Para lo cual se obtiene un modelo de pérdidas y se determinan las condiciones bajo las cuales las pérdidas se reducen. i Abstract In an electric vehicle is required to control the torque generated by the motor, this in order to imitate the operation of a vehicle with internal combustion engine. Furthermore, it is important to take care of energy consumption due to an electric vehicle has a limited amount of energy stored in batteries. This thesis presents the design of a controller for torque and magnetic flux of a three phase squirrel cage induction motor, which propels a battery powered electric vehicle. Additionally, a magnetic flow selection algorithm is developed to reduce energy consumption during operation of the vehicle. For the design of the vehicle controller and then examine their performance, a mathematical model of the electric vehicle is required. This model is obtained from analysis of individual components operation and the interaction of these during vehicle operation. The controller design is based on the principle of torque production and the mathematical model of the induction motor. From the analysis of the direct torque control follows that the electromagnetic torque developed by the induction motor can be controlled through the stator magnetic flux. To control the stator magnetic flux, and also the pair, the voltage applied to the stator of the three phase induction motor is changed. The flow selection algorithm is intended to reduce electrical losses that are presented. For this, loss model is obtained and specifying the conditions under which the losses are reduced. iii Tabla de contenido. Pág. Resumen .................................................................................................................................. i 0 89H Abstract.................................................................................................................................. iii 1H 90H Tabla de contenido. ................................................................................................................ v 2H 91H Lista de figuras ..................................................................................................................... vii 3H 92H Lista de tablas ........................................................................................................................ ix 4H 93H Simbología.............................................................................................................................. x 5H 94H Siglas ................................................................................................................................. xiv 6H 95H Capítulo 1 INTRODUCCIÓN........................................................................................................................ 1 7H 8H 96H 1.1. Planteamiento del problema. ...................................................................................... 3 1.2. Justificación. ............................................................................................................... 3 1.3. Hipótesis. .................................................................................................................... 4 9H 10H 1H 97H 98H 9H 1.4. Objetivos..................................................................................................................... 4 1.4.1. General. .................................................................................................................. 4 1.4.2. Particulares. ............................................................................................................ 5 12H 10H 13H 10H 14H 102H 1.5. Estado del Arte. .......................................................................................................... 5 1.5.1. Tipos de VE. .......................................................................................................... 5 1.5.2. Tipos de motores empleados en VE. ...................................................................... 8 1.5.3. Técnicas de control de motores empleadas en VE. .............................................. 11 15H 103H 16H 104H 17H 105H 18H 1.6. 19H 106H Organización de la tesis............................................................................................ 18 107H Capítulo 2 MODELADO DEL VEHÍCULO ELÉCTRICO. ................................................................................ 21 20H 21H 108H 2.1. Banco de baterías...................................................................................................... 22 2.2. Convertidor CD – CA (inversor). ............................................................................. 23 2.3. Motor de inducción trifásico..................................................................................... 26 2.4. Parte mecánica del VE.............................................................................................. 32 2.5. Simulación del VE en lazo abierto ........................................................................... 37 2H 23H 24H 26H 25H 109H 10H 1H 12H 13H v Capítulo 3 DISEÑO DEL CONTROLADOR .................................................................................................. 43 27H 28H 14H 3.1. Estimación de flujo y par.......................................................................................... 44 3.2. Control directo de par ............................................................................................... 46 3.3. Controlador propuesto .............................................................................................. 50 29H 30H 31H 15H 16H 17H 3.4. Simulaciones............................................................................................................. 54 3.4.1. DTC convencional................................................................................................ 55 3.4.2. Controlador propuesto .......................................................................................... 59 32H 18H 3H 19H 34H 120H Capítulo 4 ALGORITMO DE SELECCIÓN DE FLUJO .................................................................................... 65 35H 36H 12H 4.1. Análisis de la eficiencia............................................................................................ 68 4.2. Modelo de pérdidas .................................................................................................. 69 4.3. Algoritmo de selección de flujo................................................................................ 70 4.4. Simulación ................................................................................................................ 73 37H 38H 39H 40H 12H 123H 124H 125H Capítulo 5 IMPLEMENTACIÓN. CONTROL VOLTS/HERTZ ......................................................................... 81 41H 42H 126H 5.1. Control Volts/Hertz en lazo abierto.......................................................................... 84 5.2. Control Volts/Hertz en lazo cerrado......................................................................... 87 4H 43H 127H 128H Capítulo 6 CONCLUSIONES ..................................................................................................................... 91 45H 46H 129H Referencias ........................................................................................................................... 95 47H 130H Anexo 1. TIPOS DE BATERÍAS EMPLEADAS EN VE ................................................................ 101 48H 49H 13H Anexo 2. FASORES ESPACIALES .......................................................................................... 105 50H 51H 132H Anexo 3. CICLOS DE CONDUCCIÓN ...................................................................................... 113 52H 53H 13H Anexo 4. PWM VECTORIAL ................................................................................................ 117 54H 5H 134H vi Lista de figuras Pág. Figura 1.1. Diagrama a bloques de un vehículo híbrido: a) serie y b) paralelo..……………6 Figura 1.2. Diagrama a bloques de vehículo eléctrico con celdas de combustible…………7 Figura 1.3. Diagrama a bloques de un vehículo eléctrico alimentado por baterías…………7 Figura 1.4. Control directo de par con tabla de conmutación………………………………..16 Figura 1.5. Control directo de par con PWM vectorial………………………………………..17 Figura 2.1. Diagrama del VE…………………………………………………………………….22 Figura 2.2. Convertidor CD – CA………………………………………………………………..24 Figura 2.3. Motor de inducción trifásico………………………………………………………...26 Figura 2.4. Representación de la transmisión del VE………………………………………...33 Figura 2.5. Fuerzas actuantes sobre el VE en una pendiente……………………………….34 Figura 2.6. Diagrama a bloques en simulink® del VE…………………………………………38 Figura 2.7. Voltajes de fase: a) van, b) vbn, c) vcn y d) acercamiento de van…………………40 Figura 2.8. Corrientes del estator en el intervalo de a) 0 a 50s y b) 49.95 a 50s………….41 Figura 2.9. Corrientes del rotor en el intervalo de a) 0 a 50s y b) 48 a 50s………………..41 Figura 2.10. Variables mecánicas del VE: a)Par desarrollado por el MI, b) Velocidad angular del MI, c) Velocidad lineal del VE y d) Potencia desarrollada por el MI…………..42 Figura 3.1. Producción del par electromagnético……………………………………………..46 Figura 3.2. Fasores espaciales de voltaje del inversor……………………………………….48 Figura 3.3. Diagrama a bloques del DTC convencional………………………………………49 Figura 3.4. Comparadores de histéresis de: a) 2 niveles para el flujo y b) 3 niveles para el par……………………………………………………………………………………………..……….50 Figura 3.5. Diagrama a bloques del controlador propuesto………………………………….54 Figura 3.6. Diagrama del DTC convencional en Simulink®…………………………………..55 Figura 3.7. a) Velocidad vs. velocidad deseada y b) error de velocidad……………………56 Figura 3.8. a) Par deseado vs. par estimado y b) error de par………………………………57 Figura 3.9. a) Flujo deseado vs. estimado y b) error de flujo………………………………...57 Figura 3.10. Corrientes del estator: a) 0 a 22s y b) 15s a 15.1s………………………….…58 Figura 3.11. Trayectoria del flujo del estator…………………………………………………..59 Figura 3.12. Diagrama del controlador propuesto en Simulink®……………………………..59 vii Figura 3.13. a) Velocidad deseada vs. velocidad y b) error de velocidad………………….60 Figura 3.14. a) Par deseado vs. par estimado y b) error de par…………………………….61 Figura 3.15. a) Flujo deseado vs. estimado y b) error de flujo……………………………….62 Figura 3.16. Corrientes del estator: a) 0 a 22s y b) 15s a 15.1s…………………………….62 Figura 3.17. Trayectoria del flujo del estator…………………………………………………..63 Figura 4.1. Flujo magnético deseado vs. velocidad angular…………………………………66 Figura 4.2. Circuito equivalente del MI…………………………………………………………69 Figura 4.3. Circuito equivalente alternativo del MI…………………………………………….69 Figura 4.4. Algoritmo de selección de flujo…………………………………………………….73 Figura 4.5. Velocidad de referencia para el VE………………………………………………..74 Figura 4.6. a) Velocidad deseada vs. velocidad y b) error de velocidad……………………75 Figura 4.7. a) Par deseado vs. par estimado y b) error de par………………………………75 Figura 4.8. a) Flujo deseado vs. flujo estimado y b) error de flujo…………………………..76 Figura 4.9. Corrientes del estator: a) 0 a 16s y b) 8 a 8.1 s…………………………………76 Figura 4.10. Potencia de conversión……………………………………………………………77 Figura 4.11. Flujo de referencia vs. la relación Energía de salida/Energía de entrada…..78 Figura 4.12. a) Velocidad deseada vs. velocidad, b) par deseado vs. par estimado con flujo de referencia 0.4 Wb•vuelta……………………………………………………………….79 Figura 4.13. a) Velocidad deseada vs. velocidad, b) par deseado vs. par estimado con flujo de referencia 1.2 Wb·vuelta………………………………………………………………..79 Figura 5.1. Relación Frecuencia – Voltaje……………………………………………………..82 Figura 5.2. Diagrama a bloques de la implementación del control Volts/Hertz……………82 Figura 5.3. Señales del encoder a: a) 0 rad/s, y b) 93.5 rad/s……………………………….84 Figura 5.4. Diagrama a bloques en Vissim© del control Volts/Hertz en lazo abierto……..85 Figura 5.5. a) Velocidad deseada vs. velocidad medida, y b) error de velocidad…………86 Figura 5.6. a) Frecuencia, y b) amplitud normalizada del voltaje trifásico aplicado……….87 Figura 5.7. Diagrama a bloques en Vissim© del control Volts/Hertz en lazo cerrado…….88 Figura 5.8. a) Velocidad deseada vs. velocidad medida, y b) error de velocidad…………90 Figura 5.9. a) Frecuencia, y b) amplitud normalizada del voltaje trifásico aplicado……….90 Figura A2.1. Diagrama esquemático de los devanados del estator………………………107 Figura A2.2. Fasor espacial de una variable trifásica del estator………………………….108 Figura A2.3. Fasor espacial de una variable trifásica del rotor…………………………….109 Figura A2.4. Fasor espacial del estator en el MR general………………………………….110 viii Figura A2.5. Fasor espacial del rotor en el MR general…………………………………….112 Figura A3.1. Ciclos de conducción: a) FUDS, b) SFUDS, c) ECE-15, d) SAE J227a…..115 Figura A4.1. Inversor de dos niveles………………………………………………………….117 Figura A4.2. Principio del PWM vectorial…………………………………………………..…120 Figura A4.3. Señales del PWM vectorial………………………………………………………....120 Lista de tablas Pág. Tabla 2.1. Parámetros del VE. ………………………………………………………………….39 Tabla 2.2. Parámetros del MI trifásico………………………………………………………….39 Tabla 3.1. Tabla de conmutación para el DTC………………………………………………..50 Tabla 4.1. Análisis de energía en el VE………………………………………………………..78 Tabla 5.1. Equipo utilizado para el control Volts/Hertz……………………………………….83 Tabla A1.1. Especificaciones de los distintos tipos de baterías……………………………103 Tabla A3.1. Parámetros para las cuatro variaciones del SAE J227a……………...…........…115 ix Simbología A Área frontal del VE a Aceleración del VE B Coeficiente de fricción viscosa C Capacidad en Ah Cd Coeficiente aerodinámico Cp Capacidad Peukert dte Salida del comparador de par dψ Salida del comparador de flujo et Error de par eψ Error de flujo f Frecuencia Fad Fuerza de fricción con el viento Fhc Fuerza para mover el VE por una pendiente Frr Fuerza de fricción Fte Fuerza de tracción G Cociente de reducción de velocidad angular de la transmisión g Aceleración debida a la gravedad I Corriente I’r Corriente del estator Ic Corriente del núcleo Icd Corriente de la fuente de CD ir Fasor espacial de corriente del rotor ir ´ Fasor espacial de corriente del rotor en el MR estacionario Is Corriente del estator is Fasor espacial de corriente del estator is * Complejo conjugado del fasor espacial de corriente del estator isA, isB e isC, Corrientes de las tres fases del estator del MI x isx Componente del eje x (flujo) de la corriente del estator isy Componente del eje y (par) de la corriente del estator J Momento de Inercia total (rotor y VE) JMI Momento de inercia del MI JVE Momento de inercia del VE K Coeficiente Peukert k1 y k2 Ganancias del controlador de par ki Ganancia integral kp Ganancia proporcional kψ Ganancia del controlador de flujo L’r Inductancia del rotor referida al estator Lm Inductancia de magnetización Lr Inductancia total del rotor Lr Inductancia propia de los devanados del rotor Ls Inductancia total del estator Ls Inductancia propia de los devanados del estator m Masa total del vehículo Mr Inductancia mutua entre los devanados del rotor Ms Inductancia mutua entre los devanados del estator M sr Valor máximo de la inductancia mutua entre los devanados del estator y rotor P Pares de polos pi, Pi Potencia de entrada Pm Pérdidas mecánicas Pmec Potencia mecánica Po Potencia de salida Pr Pérdidas en el rotor Ps Pérdidas en el estator PT Pérdidas totales xi Px Pérdidas en el eje x Py Pérdidas en el eje y r Radio del neumático R’r Resistencia del rotor referida al estator ra, rb y rc Fases del rotor del MI Re( ) Parte real del fasor espacial Rr Resistencia de los devanados del rotor Rs Resistencia de los devanados del estator s Deslizamiento del MI Sa, Sb y Sc Señales de modulación del inversor sA, sB y sC Fases del estator del MI sign( ) Función signo T Tiempo de descarga en horas te Par electromagnético tˆe Par electromagnético estimado tL Par de carga us Fasor espacial del voltaje del estator (salida del inversor) usA, usB y usC Voltajes de las tres fases del estator del MI v Velocidad lineal del VE V Voltaje Vcd Voltaje de CD del banco de baterías Δt Incremento de tiempo Δte Bandas de tolerancia para el error de par Δψ Bandas de tolerancia para el error de flujo φmín Flujo magnético mínimo φ Ángulo de inclinación de la pendiente η Eficiencia ηg Eficiencia de la transmisión xii μrr Coeficiente de fricción θr Posición angular del rotor del MI θrm Posición angular mecánica del rotor ρ Densidad del aire ρr Ángulo del fasor espacial de enlaces de flujo del rotor ρs Ángulo del fasor espacial de enlaces de flujo del estator ψr Fasor espacial de enlaces de flujo del rotor ψ r´ Fasor espacial de enlaces de flujo del rotor en el MR estacionario ψ r´ Módulo del fasor espacial de enlaces de flujo del rotor ψs Fasor espacial de enlaces de flujo del estator ψs Módulo del fasor espacial de enlaces de flujo del estator ψˆ s Estimado del fasor espacial de enlaces de flujo del estator ωg Velocidad angular del MR general ωr Velocidad angular del rotor del MI ωrm Velocidad angular mecánica del rotor ωs Frecuencia angular del estator xiii Siglas VE Vehículo Eléctrico CD Corriente Directa CA Corriente Alterna PWM Modulación por Ancho de Pulso, por sus siglas en inglés Pulse Wide Modulation MI Motor de Inducción MR Marco de Referencia PI Proporcional–Integral DSP Procesador digital de señales, por sus siglas en inglés Digital Signal Processor VSI Inversor con Fuente de Voltaje, por sus siglas en inglés Voltage Source Inverter CSI Inversor con Fuente de Corriente, por sus siglas en inglés Current Source Inverter DTC Control Directo de Par, por sus siglas en inglés Direct Torque Control FUDS Ciclo de manejo federal urbano, por sus siglas en inglés Federal Urban Driving Schedule SFUDS Ciclo de manejo simplificado federal urbano, por sus siglas en inglés Simplified Federal Urban Driving Schedule SAE Asociación de Ingenieros Automotrices, por sus siglas en inglés Society of Automotive Engineers xiv Capítulo 1. INTRODUCCIÓN. Actualmente la gran mayoría de los vehículos en uso son de combustión interna y hasta el momento han sido un medio de transporte adecuado. Sin embargo, tienen ciertos inconvenientes, entre ellos el problema de contaminación, atmosférica y auditiva, que ocasionan. Aunado a esto se tiene el problema de la escasez de combustible que se prevé en los próximos años. Existe la tendencia mundial a utilizar medios de transporte más amigables con el medio ambiente, lo que ha motivado la búsqueda de alternativas para sustituir a los vehículos de combustión interna y reducir las emisiones contaminantes. Por otra parte, para evitar el problema de desabasto de combustible, los vehículos que se desarrollen de ahora en adelante deberán ser propulsados por una forma de energía de gran flexibilidad, fácil de distribuir y que pueda provenir de distintas fuentes. La energía eléctrica cumple con todas las características antes mencionadas. También se busca que los vehículos resultantes sean capaces de competir con los vehículos de combustión interna en costo, peso, rango de recarga (autonomía), confiabilidad, eficiencia, velocidad máxima y aceleración, entre otras características. Los vehículos eléctricos presentan una excelente alternativa al uso indiscriminado de hidrocarburos y a los problemas de la contaminación atmosférica. Sin embargo, presentan el problema de tener escasa autonomía y prolongados 1 Capítulo 1. Introducción tiempos de recarga. Un vehículo eléctrico (VE) se caracteriza por usar tracción eléctrica, es decir, su movimiento es proporcionado por un motor eléctrico en lugar del motor de combustión interna comúnmente usado. Existen diferentes tipos de VE cuya principal diferencia es la fuente primaria de energía. Así, se tienen VE en base a celdas de combustible y VE alimentados por baterías (Larminie y Lowry, 2003). El uso de tracción eléctrica para los automóviles, contribuye a la disminución de la contaminación ambiental, en particular la contaminación del aire y acústica. Esta disminución de la contaminación es importante en el contexto del problema del calentamiento global que enfrenta el planeta. Asimismo, la utilización de transporte limpio contribuye a un mejoramiento de la calidad de vida principalmente en las grandes ciudades. El VE presenta un número significativo de ventajas con respecto al de combustión interna. Entre las principales se pueden mencionar (Conae, 2002): • Son más eficientes que los vehículos con motor de combustión interna. • No producen emisiones contaminantes en el lugar de operación. • Sustantiva simplificación mecánica. • Bajo ruido. • Tienen costos de mantenimiento menores. • Son más confiables que los vehículos con motor de combustión interna. • El sistema de frenado puede tener la capacidad regenerativa de potencia, lo que reduce las pérdidas de energía. • Amplia variedad de fuentes de energía. Un VE es un sistema electromecánico bastante complejo, cuyas entradas de control son las señales enviadas por el conductor a través de los pedales de aceleración y freno. El motor eléctrico que impulsa al VE es parte fundamental del sistema de tracción, y por tanto las estrategias de control utilizadas en motores eléctricos se pueden extrapolar a VE. Se han utilizado tanto motores de corriente 2 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía directa (CD) como corriente alterna (CA) para impulsar VE, mostrando estos últimos mejores características, entre las cuales destacan: ausencia de escobillas, relación potencia/peso, relación par/peso y costo (Zeraouila et al, 2005). 1.1. Planteamiento del problema. Los principales problemas que presentan actualmente los VE son: 1. tienen una autonomía menor que los vehículos de combustión interna, y 2. presentan tiempos de recarga prolongados. Estos problemas se deben a que el VE cuenta con una fuente limitada de energía, que son las baterías. En los últimos años se han desarrollado baterías con mejores prestaciones, sin embargo todavía no satisfacen los requerimientos del VE. Debido a esto, el uso de la energía en los VE debe ser lo más eficiente posible. Por tanto, en este trabajo se plantea diseñar un sistema de control para un VE que reduzca las pérdidas de energía y utilice frenado regenerativo para recuperar parte de la energía cinética del VE al momento de disminuir la velocidad del vehículo. 1.2. Justificación. En un VE es fundamental hacer un buen uso de la energía eléctrica, debido a que sólo se cuenta con una cantidad limitada de esta, almacenada en las baterías. El tratar de aumentar la energía disponible nos llevaría a alguna de las siguientes opciones: 1. Aumentar el número de baterías, lo que incrementaría el peso del VE, el volumen que ocupan las baterías en el VE y el costo. 3 Capítulo 1. Introducción 2. Cambiar el tipo de baterías empleadas por otras de mayor capacidad y mayor energía específica, incrementando significativamente el costo. Hacer un buen uso de la energía eléctrica conlleva a reducir las pérdidas de energía y al mismo tiempo recuperar energía durante el frenado. Por lo tanto, uno de los objetivos de control en el VE debe ser reducir las pérdidas de energía conservando un desempeño dinámico adecuado. Por otra parte, el frenado regenerativo permite recuperar parte de la energía cinética del VE, en lugar de perderla en forma de calor como se hace en el frenado convencional de vehículos. 1.3. Hipótesis. Utilizando un controlador basado en la técnica de control directo de par y con modulación PWM vectorial, es posible elegir un flujo magnético para lograr el desempeño deseado con un uso eficiente de la energía mediante la disminución de las pérdidas y la recuperación de energía durante el frenado. 1.4. Objetivos. 1.4.1. General. Diseñar un controlador basado en la técnica de control directo de par para un vehículo eléctrico impulsado por un motor de inducción trifásico, considerando frenado regenerativo, sin medición de: par, flujo, velocidad ni posición, incorporando además un algoritmo de selección de flujo magnético que reduzca las pérdidas. 4 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía 1.4.2. • Particulares. Analizar el funcionamiento y los componentes que forman un VE alimentado por baterías. • Obtener el modelo matemático del VE y de cada una de sus partes fundamentales. • Simular el funcionamiento en lazo abierto del VE. • Analizar la técnica de control directo de par para VE. • Diseñar un controlador no lineal de par y flujo para el motor de tracción del VE. • Examinar el desempeño del controlador mediante simulación. • Desarrollar un algoritmo de selección de flujo que permita reducir las pérdidas de energía. • Examinar el desempeño del algoritmo de selección de flujo mediante simulación. 1.5. Estado del Arte. 1.5.1. Tipos de VE. Entre los tipos de vehículos con tracción eléctrica se encuentran los híbridos, los eléctricos alimentados por baterías y eléctricos con celdas de combustible (Larminie y Lowry, 2003). Los vehículos eléctricos no usan motores de combustión interna y su principal diferencia es la fuente primaria de energía. Vehículos híbridos. En la figura 1.1 se muestran los diagramas de los vehículos híbridos, los cuales se caracterizan por tener tanto un motor de combustión como un motor eléctrico. En el vehículo híbrido tipo serie el motor de combustión tiene la función de 5 Capítulo 1. Introducción recargar las baterías por medio de un generador y el motor eléctrico es el encargado de proporcionar la potencia mecánica para mover al vehículo. Mientras que, en el vehículo híbrido en paralelo, el movimiento del vehículo puede ser proporcionado por el motor de combustión interna, por el motor eléctrico o por ambos; la interconexión de estos dos motores se realiza por medio de la transmisión. Motor de combustión interna Generador eléctrico Convertidor Electrónico Motor eléctrico Transmisión Conexión eléctrica Conexión mecánica Neumático Banco de Baterías a) b) Figura 1.1. Diagrama a bloques de un vehículo híbrido: a) serie y b) paralelo. Vehículos eléctricos con celdas de combustible. En la figura 1.2 se muestra un diagrama a bloques del VE que utiliza Celdas de Combustible. Las celdas de combustible generan un voltaje por medio de una reacción química, sin embargo este voltaje tiene un valor bajo, por lo cual es 6 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía necesario elevarlo por medio de un convertidor CD–CD a un nivel adecuado para poder recargar las baterías. Figura 1.2. Diagrama a bloques de vehículo eléctrico con celdas de combustible. Vehículos eléctricos con baterías. En la figura 1.3 se muestra un VE que usa un banco de baterías eléctricas; el cual está constituido principalmente por la fuente primaria de energía (banco de baterías), el sistema de accionamiento del motor eléctrico (convertidores electrónicos de potencia) y el tren motriz (motor y sistema de engranaje mecánico). Figura 1.3. Diagrama a bloques de un vehículo eléctrico alimentado por baterías. La parte fundamental de un VE es el sistema de propulsión, formado por el motor, el convertidor electrónico y el controlador (Singh et al, 2006). Este es el tipo 7 Capítulo 1. Introducción de vehículo considerado en este trabajo, por lo que en el siguiente capítulo se trata más a fondo su funcionamiento. 1.5.2. Tipos de motores empleados en VE. El motor eléctrico es una parte fundamental del sistema de propulsión de un VE, las características deseadas de dicho sistema de propulsión son (Faiz et al, 2003): • Un valor elevado de los cocientes par/inercia y potencia/peso. • Alta capacidad de par máximo (300 a 400% del par nominal). • Alta velocidad. • Bajo nivel de ruido audible. • Poco mantenimiento. • Tamaño pequeño. • Bajo peso. • Costo razonable. • Alta eficiencia en un amplio rango de velocidades. • Recuperación de energía durante el frenado. Existen diversos tipos de motores eléctricos que pueden emplearse para impulsar VE, entre los cuales se encuentran los motores de CD y los motores de CA (inducción y síncronos). A continuación se describen las principales características de funcionamiento de estos motores. Motores de CD. El control de flujo y par en el motor de CD es relativamente simple. En particular para el motor de CD de excitación separada, el flujo se controla por medio 8 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía de la corriente del devanado de campo y el par por medio de la corriente del devanado de armadura. Este tipo de control nos da una respuesta rápida y un buen desempeño. Sin embargo, los motores de CD presentan algunas desventajas, muchas de las cuales se deben a la presencia del conmutador y las escobillas. Por tanto, los motores de CD requieren mantenimiento periódico, no pueden ser usados en ambientes explosivos o corrosivos, están limitados por el conmutador para funcionar a altas velocidades y/o altos voltajes. Motores de Inducción. Un motor de inducción (MI) trifásico es simples en su construcción, requiere poco mantenimiento, es más económico y pequeño comparado con el de CD. Una desventaja de los motores de inducción trifásicos es el tener un control de par y flujo relativamente más complicado que el control de los motores de CD. El poco mantenimiento y bajo costo de las máquinas de inducción las convierte en una alternativa atractiva para varias aplicaciones. Los motores de inducción trifásicos con rotor tipo jaula de ardilla son los más adecuados para aplicaciones de accionamiento eléctrico de un vehículo (Zeraouila et al, 2005). Los motores de inducción son rentables y adecuados en términos de tamaño, peso, velocidad de rotación, eficiencia, control y fiabilidad (Karlis et al, 2006). Los circuitos de potencia empleados para motores de CD son relativamente simples. En cambio, para los motores de CA hay una gran variedad de circuitos de potencia, existen por ejemplo: inversores alimentados por voltaje, alimentados por corriente, de conmutación natural, de conmutación forzada y cicloconvertidores. La máquina eléctrica y su controlador son la parte fundamental de un VE (Liu et al, 2005). Por tanto es necesario enfocar las estrategias de control en la máquina que impulsará al VE. Para un VE es recomendable el control de par en lugar del 9 Capítulo 1. Introducción control de velocidad, debido a que de esta manera se imita la operación de un vehículo con motor de combustión interna (Trounce et al, 2001). El modelo matemático del MI trifásico es de alto orden, no lineal, fuertemente acoplado y multivariable, es decir, es un sistema de ecuaciones no lineales difícil de resolver, para el cual su control es muy complejo y de gran dificultad cuando se busca la operación en un amplio rango de velocidades (Liu et al, 2005). Para lograr su simplificación se realizan una serie de transformaciones a distintos marcos de referencia entre los cuales se encuentran, el fijo al estator, el fijo al rotor y el síncrono. Motores síncronos. Los motores síncronos trifásicos son estructuralmente muy similares a los motores de inducción trifásicos, y sólo difieren en la construcción de su rotor. Así, se tienen motores síncronos: • de imanes permanentes, • de rotor devanado, y • de reluctancia variable. De estos tres tipos de motores síncronos, los que más aceptación han tenido en aplicaciones de tracción son los de imanes permanentes, superando en algunas características a los motores de inducción tipo jaula de ardilla, como son: relación potencia/peso y relación par/peso. Sin embargo, el costo de estos motores es todavía una limitante, por lo que los motores de inducción trifásicos tipo jaula de ardilla siguen siendo la mejor opción en aplicaciones de tracción (Zeraouila et al, 2005). 10 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía Los motores síncronos de rotor devanado tienen la desventaja de contar con escobillas, lo que aumenta el mantenimiento, además necesitan un voltaje de alimentación de CD para el devanado del rotor. Debido a esto no son adecuados para aplicaciones de tracción. Por otra parte, el motor síncrono de reluctancia variable ha ganado mucho interés en aplicaciones de tracción debido a su construcción robusta y su característica par–velocidad. Sin embargo tienen entre sus principales desventajas el tener ruido audible y un rizo de par elevado. 1.5.3. Técnicas de control de motores empleadas en VE. Entre los diversos controladores que se utilizan para motores de CA con aplicación de tracción, se encuentra el control directo de par y el control vectorial, los cuales tienen como características el tener un buen desempeño dinámico con rápida respuesta. Por otra parte, el control directo de par es más simple de implementar que el control vectorial, debido a que en este último es necesario realizar una transformación (en línea) al marco de referencia (MR) adecuado para poder realizar el desacoplo del control de par y flujo, dicha transformación no es necesaria en el control directo de par. En un motor de CA utilizado para tracción se deben controlar fundamentalmente el par y el flujo magnético. El par de referencia es proporcionado por el conductor a través del pedal del acelerador, el flujo de referencia en cambio debe de establecerse por medio del algoritmo de control. Existen dos enfoques para establecer el flujo de referencia: el primero de ellos busca obtener el máximo par disponible, y el segundo de ellos busca reducir las pérdidas de energía manteniendo un desempeño dinámico adecuado. Este último enfoque es más útil en VE debido al que la energía disponible es limitada. 11 Capítulo 1. Introducción El controlador del VE debe responder a la demanda de par establecida por el conductor. La posición del pedal del acelerador establece el par de referencia como una fracción del par máximo disponible. De manera similar la primera porción del pedal del freno es usada para el frenado regenerativo, mientras la porción restante activa el sistema de frenado convencional. Las principales técnicas de control reportadas para VE son el control vectorial y el control directo de par. Estos dos métodos tienen varios aspectos en común, tales como, control de par y flujo, rápida respuesta, y sensibilidad a ciertos parámetros del motor. En el control vectorial se controla generalmente la componente directa del flujo del rotor en el MR síncrono, mientras que en el control directo de par se controla el flujo del estator. La inductancia de magnetización, la resistencia del rotor y la inductancia del rotor son relevantes en el control vectorial, mientras que en el control directo de par la resistencia del estator juega un papel fundamental (Bazzi et al, 2009). Control Vectorial. Con el control vectorial se ha logrado la aplicación de motores de inducción y síncronos en VE con buenos resultados. El control vectorial fue introducido en Alemania hace 40 años por Blaschke (Blaschke, 1972). Para utilizar el control vectorial es necesario referir la operación del motor de inducción al MR que gira a la velocidad de sincronismo, este MR se alinea a alguno de los flujos del motor: del rotor, del estator o de magnetización (Vas, 1998). Siendo el control vectorial orientado al flujo del rotor el más comúnmente empleado (Vasudevan y Arumugam, 2004). 12 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía Al igual que en el control de motores de CD, el control vectorial en motores de CA se realiza por medio de las corrientes del motor. Sin embargo, a diferencia de los motores de CD, en motores de CA se deben controlar tanto la magnitud como el ángulo del vector de corriente. Esta es la razón por la cual se le llama control vectorial. Por otra parte, en los motores de CD la orientación del flujo magnético y fuerza magnetomotriz de la armadura es fijada por el conmutador y las escobillas, mientras que en los motores de CA esta orientación requiere de un control externo. Con el control vectorial, el vector de corriente se divide en 2 componentes, una encargada de controlar el flujo y otra de controlar el par. Con esto se consigue desacoplar el control de flujo y par logrando una respuesta transitoria similar a la del motor de CD de excitación separada. Controladores Proporcional–Integral (PI) regulan las componentes del vector de voltaje del estator para lograr el vector de corriente del estator deseado. El control vectorial puede ser directo e indirecto. En el control vectorial directo, se considera que la magnitud y la posición del vector de flujo magnético están disponibles y se conocen con precisión, es decir, son medibles o se cuenta con una estimación por medio de un observador no lineal (Ouhrouche et al, 2002), (Jian et al, 2008), (Dilmi y Yurkovich, 2005). En cambio, para el control vectorial indirecto, la magnitud y posición del vector de flujo magnético se obtienen analíticamente, mediante las ecuaciones que modelan al motor (Ouhrouche et al, 2003), (Liu et al, 2005), (Yi y Kaiqi, 2005). El control vectorial indirecto es más sencillo de implementar (comparado con el control vectorial directo), sin embargo, para este tipo de controlador es necesario calcular la velocidad de deslizamiento, lo cual involucra la constante de tiempo del rotor dependiente principalmente de la temperatura. Un valor incorrecto de la constante de tiempo del rotor resulta en el desacoplamiento incompleto del control del flujo y del par, lo cual lleva a: incrementar la disipación del motor, disminuir la eficiencia del sistema, un gran rizo en el par y un mal desempeño del sistema (Liu et al, 2005). Por lo tanto, para mantener la orientación del flujo, la 13 Capítulo 1. Introducción variación de la constante de tiempo del rotor (y en especial de la resistencia del rotor) debe ser tomada en cuenta. Se han utilizado diversos métodos para corregir el efecto de la variación de la constante de tiempo del rotor, entre los cuales se encuentran: a) Modificar la constante de tiempo del rotor por medio de la medición de la temperatura (Liu et al, 2005). b) Estimar la constante de tiempo del rotor por medio de un filtro de Kalman (Ouhrouche et al, 2003). c) Aplicación de control a la frecuencia de deslizamiento (Yi y Kaiqi, 2005). d) Estimación de la resistencia del rotor por medio de una red neuronal artificial (Huerta González et al, 2008). De acuerdo con (Vasudevan y Arumugam, 2004) las ventajas del control vectorial son: i. Sistema relativamente simple de buen desempeño. ii. Una técnica probada que ha sido utilizada durante bastante tiempo. Y sus desventajas son: i. Su desempeño puede disminuir debido a los controladores PI que involucra. ii. Error en los parámetros causa errores en el control de par y del flujo. El control vectorial tiene la desventaja de necesitar transformación de coordenadas en línea para desacoplar la interacción entre el control del flujo y el par. De aquí que el algoritmo computacional es complejo y su implementación usualmente requiere un procesador digital de señales (DSP, por sus siglas en inglés Digital Signal Processor) de alto desempeño (Singh et al, 2006). 14 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía La elección del flujo de referencia es de suma importancia en el control vectorial. La forma tradicional de elegir el flujo de referencia busca generar el máximo par y evitar la saturación magnética y se debilita a medida que aumenta la velocidad del rotor, para limitar las corrientes y voltajes del estator. Por tanto el flujo de referencia se mantiene constante desde velocidad cero hasta la velocidad base y se disminuye en una proporción inversa a la velocidad por encima de esta velocidad base. Este flujo de referencia tradicional se utiliza en los trabajos de (Liu et al, 2005), (Jian et al, 2008), (Pinewski, 1997) y (Ouhrouche et al, 2003). Otra forma de elegir el flujo de referencia es buscar minimizar el consumo de energía eléctrica, esta forma es muy útil en VE debido a que la cantidad de energía disponible es limitada. En (Wu et al, 2008), (Dilmi y Yurkovich, 2005) y (Ta y Hori, 2001) utilizan referencias de flujo buscando una reducción de la energía utilizada. Control directo de par. El control directo de par fue introducido hace mas de 25 años por Takahashi (Takahashi y Noguchi, 1986) en Japón y por Depenbrock (Depenbrock, 1985) en Alemania. El control directo de par tiene la ventaja sobre el control vectorial de no necesitar hacer transformaciones a un MR giratorio. El sistema de propulsión de VE utilizando motores de inducción con la técnica de control directo de par ha logrado gran popularidad debido a la rápida respuesta y configuración sencilla. Este método permite un control preciso y rápido del flujo y el par del MI. Esta estrategia de control se utiliza ampliamente en VE (Singh et al, 2006). En el control directo de par se controlan directa e independientemente el flujo y par por medio de la selección óptima de los modos de conmutación del inversor. 15 Capítulo 1. Introducción Con este control se logra una rápida respuesta dinámica, una frecuencia de conmutación baja, y una reducción de armónicos (Vas, 1998). En el control directo de par se utilizan las mediciones de voltajes y corrientes en el estator para estimar los enlaces de flujo del estator y el par electromagnético (Faiz y Sharifian, 2001). Esta estimación depende directamente de la resistencia del 56H 57H estator. Es posible también estimar la velocidad y posición del motor pero esto involucra la dependencia de otros parámetros del motor como son la inductancia de magnetización y la resistencia del rotor (Bazzi et al, 2009). En el control directo de par convencional (ver figura 1.4) se utiliza una tabla para determinar las conmutaciones del inversor, las entradas de dicha tabla son las salidas de comparadores de histéresis del error de flujo y del error de par (Faiz et al, 2003). Esta técnica de conmutación es muy simple y fácil de implementar, sin embargo tiene el inconveniente de que la frecuencia de conmutación no es constante (Idris et al, 2006). ma ref Tabla de conmutación est mb Inversor ic mc ref ia ib Motor de Inducción est Vcd Estimador de flujo y par Figura 1.4. Control directo de par con tabla de conmutación. 16 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía Existen otras técnicas de conmutación que se emplean en conjunto con el control directo de par, tal es el caso de la modulación por ancho de pulso (PWM, por sus siglas en inglés Pulse Wide Modulation) vectorial (Haddoun et al, 2007), (Bazzi et al, 2009) (Jianguo y Quanshi, 2005) que tiene frecuencia de conmutación constante. El diagrama a bloques para el control directo de par con PWM vectorial se muestra en la figura 1.5. La modulación PWM vectorial es una de las técnicas de conmutación más importante para inversores con fuente de voltaje, debido a que proporciona: un amplio rango de control lineal, poca distorsión armónica, rápida respuesta e implementación digital sencilla. El principio de PWM vectorial está basado en la conmutación entre dos vectores adyacentes y dos vectores cero, durante un periodo de conmutación. Para calcular la duración del ciclo de conmutación se usa el concepto de vectores espaciales. ma ref Control directo de par est PWM vectorial mb Inversor ia ib ic mc ref Motor de Inducción est Vcd Estimador de flujo y par Figura 1.5. Control directo de par con PWM vectorial. De acuerdo con (Vasudevan y Arumugam, 2004) las ventajas del control directo de par son: i. Rápida respuesta del par. ii. Relativamente simple. 17 Capítulo 1. Introducción iii. No requiere de sensores de velocidad ni posición. Y sus desventajas son: i. Alta distorsión de corriente, lo que aumenta las pérdidas. ii. Rizo de par elevado. iii. Frecuencia de conmutación variable. El uso de control directo de par con PWM vectorial es una excepción que exhibe rápida respuesta de par y poca distorsión en la corriente y el par. Al igual que en el control vectorial, en el control directo de par se puede elegir el flujo magnético de forma tradicional, para obtener el máximo par como en (Faiz y Sharifian, 2001), (Singh et al, 2006). O se puede elegir de manera que se minimicen las pérdidas de energía para hacer más eficiente al VE (Faiz et al, 2002), (Haddoun et al, 2007). Solamente en algunos trabajos se considera la dinámica del VE en conjunto con el control directo de par (Khoucha et al, 2007), (Haddoun et al, 2007). 1.6. Organización de la tesis. El resto de esta tesis está organizado de la siguiente manera: En el capítulo 2 se presenta la estructura básica de un VE, considerando los componentes fundamentales que los forman. Posteriormente se presentan las ecuaciones matemáticas que describen el funcionamiento de cada uno de los componentes del VE y la interacción entre ellos. Para finalizar el capítulo se tienen las simulaciones del funcionamiento del vehículo en lazo abierto. 18 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía El diseño del controlador se trata en el capítulo 3. La estimación de flujo del estator y el par del MI es el primer tema abordado en este capítulo. Para el diseño del controlador se parte de un análisis del principio de funcionamiento del control directo de par. Posteriormente se describe el procedimiento de diseño del controlador propuesto, el cual tiene como base el control directo de par y la ecuación que modela el estator del MI. Las simulaciones realizadas para examinar el desempeño, tanto del control directo de par como del controlador propuesto, se presentan al final de este capítulo. El capítulo 4 se dedica al análisis al desarrollo del algoritmo de selección de flujo para reducir las pérdidas en el VE. Se comienza con un análisis de la eficiencia del VE, para los cual se utiliza un modelo de pérdidas del MI. Usando el modelo de pérdidas se determinan las condiciones para reducirlas y se plantea el algoritmo de selección del flujo. Se presentan simulaciones donde se observa que el cambio en el flujo magnético influye en el consumo de energía en el VE. La implementación del control Volts/Hertz se presenta en el capítulo 5, donde se describe el principio de operación del control Volts/Hertz, así como los dispositivos utilizados para las pruebas experimentales realizadas. También se presentan los resultados experimentales del control Volts/Hertz tanto en lazo abierto como en lazo cerrado. Las conclusiones del trabajo realizado se encuentran en el capítulo 6. Posteriormente se enlistan las referencias consultadas para el desarrollo del trabajo. 19 Capítulo 1. Introducción Adicionalmente, se tratan algunos tópicos útiles para la mejor comprensión de este trabajo como son: • Anexo 1. Tipos de baterías empleadas en VE. • Anexo 2. Fasores espaciales. • Anexo3. Ciclos de conducción. • Anexo 4. PWM vectorial. 20 Capítulo 2. MODELADO DEL VEHÍCULO ELÉCTRICO. En el presente capítulo se desarrolla el modelo matemático del VE cuyo diagrama se muestra en la figura 2.1, el cual está conformado esencialmente por: • Banco de baterías. En este se almacena la energía necesaria para que el vehículo pueda funcionar por un tiempo determinado. En los bancos de baterías suelen utilizarse conexiones en paralelo o arreglos paralelo–serie. • Convertidor CD-CA (inversor). El voltaje proporcionado por las baterías es de CD, y el motor empleado es un motor de CA. Por lo tanto, es necesario un dispositivo capaz de realizar la conversión de CD–CA para hacer la interconexión entre baterías y motor. • Motor de inducción trifásico. Es el encargado de proporcionar el movimiento del VE, en el se realiza la conversión de energía eléctrica a energía mecánica y viceversa. El MI el alimentado por el convertidor CD– CA y su eje es acoplado a la transmisión. • Parte mecánica del VE. Está constituida por la transmisión, las ruedas, y la masa total de sus componentes (baterías, convertidores electrónicos, motor/generador eléctrico, transmisión, carrocería, chasis, etc.). Por medio de la transmisión y las ruedas el movimiento giratorio del motor es convertido a movimiento lineal del vehículo. 21 Capítulo 2. Modelado del vehículo eléctrico Figura 2.1. Diagrama del VE. También cabe señalar que el VE se puede subdividir en una parte eléctrica/electrónica y en una parte mecánica. El MI forma parte tanto de la parte eléctrica como de la mecánica debido a que en este dispositivo se realiza la conversión de energía de eléctrica a mecánica y viceversa. A continuación se describe el funcionamiento de cada uno de los componentes del VE mencionados anteriormente haciendo énfasis en las ecuaciones matemáticas que los modelan con el objetivo de poder simular su desempeño. Asimismo, se analiza su funcionamiento con la interconexión mostrada en la figura 2.1, para obtener el modelo matemático del VE. 2.1. Banco de baterías. El banco de baterías juega un papel muy importante en los VE, debido a que en este se almacena la energía de la cual dispone el vehículo para moverse. Una de las características del VE que está estrechamente relacionada con el banco de baterías es su autonomía, es decir, la distancia que puede recorrer sin necesidad de recargar las baterías. En el anexo 1 se presentan los tipos de baterías empleadas en VE y sus principales características. 22 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía Para el modelado del VE utilizado en este trabajo, el banco de baterías se supone con un funcionamiento ideal, es decir, se considera como una fuente de voltaje de CD constante. Dicho banco de baterías está formado por 25 baterías de 12 V conectadas en serie. 2.2. Convertidor CD – CA (inversor). Para hacer funcionar el motor eléctrico del VE a partir del banco de baterías es necesario contar con un convertidor electrónico de potencia capaz de convertir el voltaje de CD de las baterías en un voltaje de CA trifásico. Dicho convertidor se conoce como convertidor CD – CA trifásico, o simplemente inversor trifásico. Los convertidores CD – CA tienen por objetivo la transformación de tensión CD a tensión CA de amplitud y/o frecuencia variable dependiendo de la aplicación. El proceso de conversión de voltaje se logra mediante la implementación de técnicas de modulación; dependiendo de la técnica usada se pueden mejorar: las características de eficiencia en conversión, contenido armónico en la salida y pérdidas en los componentes. Los convertidores CD – CA se clasifican como inversores con fuente de voltaje (VSI, por sus siglas en inglés Voltage Source Inverter) e inversores con fuente de corriente (CSI, por sus siglas en inglés Current Source Inverter). Los CSI se usan en sistemas de alta potencia, los VSI se reservan para aplicaciones en baja y mediana potencia. Dentro de esta clasificación existen varias configuraciones de convertidores CD – CA que dependen de la aplicación final y el nivel de voltaje o corriente de su salida. En el caso de la aplicación del control de motores de baja y mediana potencia, la topología típica es el inversor trifásico con fuente de voltaje, formado por tres 23 Capítulo 2. Modelado del vehículo eléctrico inversores monofásicos de medio puente, como el mostrado en la figura 2.2, constituido por seis elementos de conmutación (IGBTs en este caso) y seis diodos en antiparalelo. Figura 2.2. Convertidor CD – CA. Vcd representa el voltaje de CD del banco de baterías. El voltaje de CA trifásico es obtenido de las terminales a, b y c. Las señales de modulación Sa, Sb y Sc sólo pueden tomar el valor de 0 o 1; si por ejemplo, Sa es igual a 1, se activa el interruptor superior de la primera rama, de izquierda a derecha, quedando la terminal “a” conectada a Vcd; si por el contrario, Sa es igual a 0, se activa el interruptor inferior de la misma rama y la terminal “a” es conectada a tierra, lo mismo sucede para la segunda y tercera rama con las señales Sb y Sc, respectivamente. En la teoría de circuitos de CA es común representar las cantidades sinusoidales variantes en el tiempo (voltajes y corrientes) por medio de fasores complejos (Vas, 1993). Con esto se tiene una forma simple de obtener soluciones para circuitos de CA Un conjunto de variables trifásicas (ya sean voltajes, corrientes o enlaces de flujo) pueden expresarse mediante un fasor espacial, dicha representación consiste en número complejo cuya magnitud y ángulo pueden variar 24 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía con el tiempo (Vas, 1998). En el anexo 2, se presenta una introducción al tema de fasores espaciales para el lector interesado en el tema. El fasor espacial del voltaje de salida del inversor us depende del valor de Vcd y de las señales de modulación Sa, Sb y Sc, como se expresa en la siguiente ecuación: 2 us = Vcd ⎡⎣1 S a + a Sb + a 2 Sc ⎤⎦ 3 donde a = e j2π/3 2 ya =e (2.1) j4π/3 . Por su parte la corriente Icd demandada a la fuente de CD (banco de baterías) está dada por: I cd = isA Sa + isB Sb + isC Sc (2.2) Siendo isA, isB e isC, las corrientes de las fases a, b y c, indicadas en la figura 2.2. Asimismo, la potencia de entrada al inversor pi, entregada por el banco de baterías del VE, se puede calcular mediante. pi ( t ) = Vcd I cd = Vcd ( isA Sa + isB Sb + isC Sc ) (2.3) Por tanto, la corriente en el bus de CD y la potencia de entrada varían con las señales Sa, Sb y Sc, y con las corrientes del estator del MI. 25 Capítulo 2. Modelado del vehículo eléctrico 2.3. Motor de inducción trifásico En esta sección se presenta el modelo del MI trifásico tipo jaula de ardilla haciendo uso de fasores espaciales. El uso de fasores espaciales en el análisis de máquinas eléctricas de CA es de gran ayuda ya que simplifica la representación matemática y facilita el análisis. El MI trifásico tipo jaula de ardilla cuenta con un devanado trifásico en el estator, y en el rotor cuenta con una jaula de ardilla que, para propósitos de análisis, se puede considerar como un devanado trifásico con voltaje de alimentación igual a cero. En la figura 2.3 se presenta un diagrama del MI trifásico tipo jaula de ardilla (Ong, 1998), donde se muestran las tres fases del estator sA, sB y sC, y las tres fases del rotor ra, rb y rc. θr es la posición angular del rotor y ωr es la velocidad angular del rotor. Figura 2.3. Motor de inducción trifásico. Las dos ecuaciones de voltajes de Kirchhoff, una para el estator y una para el rotor, que modelan la parte eléctrica del MI son: dψ s dt dψ r 0 = Rr ir + dt us = Rs is + 26 (2.4) Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía donde us es el fasor espacial de voltaje del estator, is es el fasor espacial de corriente del estator, ψ s es el fasor espacial de enlaces de flujo del estator, Rs es la resistencia de los devanados del estator, ir es el fasor espacial de corriente del rotor, ψ r es el fasor espacial de enlaces de flujo del rotor y Rr es la resistencia de los devanados del rotor. Cabe señalar que en (2.4) cada ecuación está en su MR natural, es decir, la 135H ecuación de voltajes del estator está en el MR estacionario (fijo al estator) y la ecuación de voltajes del rotor está en el MR fijo al rotor. Es común encontrar el modelo de la parte eléctrica del MI refiriendo ambas ecuaciones (estator y rotor) al mismo MR. Para el control directo de par se utiliza el modelo de la parte eléctrica del MI en el MR estacionario: dψ s dt dψ ´ 0 = Rr ir ´+ r − jωrψ r ´ dt us = Rs is + (2.5) Solamente la ecuación del rotor se cambió al MR estacionario, debido a que la del estator ya se encontraba en este MR. ir ´ es el fasor espacial de corriente del rotor en el MR estacionario y ψ r ´ es el fasor espacial de enlaces de flujo del rotor en el MR estacionario. Los fasores espaciales de los enlaces de flujo del estator y rotor en el MR estacionario están dados por: ψ s = Ls is + Lm ir ´ ψ r ´= Lr ir ´+ Lm is 27 (2.6) Capítulo 2. Modelado del vehículo eléctrico donde: Ls = Ls − M s Lr = Lr − M r (2.7) 3 Lm = M sr 2 Ls es la inductancia total del estator, Ls es la inductancia propia de los devanados del estator, M s es la inductancia mutua entre los devanados del estator, Lr es la inductancia total del rotor, Lr es la inductancia propia de los devanados del rotor, M r es la inductancia mutua entre los devanados del rotor, Lm es la inductancia de magnetización y M sr es el valor máximo de la inductancia mutua entre los devanados del estator y rotor. También es útil contar con el modelo del MI en el MR general, ya que a partir de este se puede encontrar fácilmente el modelo del MI en cualquier MR, simplemente sustituyendo la velocidad del MR general por la velocidad del MR deseado. El modelo del MI en el MR general es: usg = Rs isg + 0 = Rr irg + dψ sg dt dψ rg dt + jω gψ sg + j (ω g − ωr )ψ rg (2.8) donde todos los fasores espaciales del estator y rotor están referidos al MR general el cual gira a una velocidad angular ωg. 28 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía Para determinar el par electromagnético que desarrolla el MI se hace uso del análisis de potencias. Como se expresa en la ecuación (2.9), la potencia instantánea 136H de entrada al MI es igual a la suma de las potencias instantáneas en los tres devanados del estator. En el rotor no existe entrada de potencia debido a que se trata de un motor tipo jaula de ardilla, y por tanto el voltaje de alimentación en el rotor es cero. pi ( t ) = usA (t )isA (t ) + usB (t )isB (t ) + usC (t )isC (t ) (2.9) usA(t), usB(t) y usC(t) son los voltajes instantáneos de las tres fases del estator, mientras que isA(t), isB(t) e isC(t) son las corrientes instantáneas respectivas. La potencia instantánea dada en (2.9), se puede expresar también en términos de los 137H fasores espaciales de voltaje y corriente del estator. 3 pi ( t ) = Re ( us is * ) 2 (2.10) us es el fasor espacial de voltaje del estator e is * es el complejo conjugado del fasor espacial de corriente del estator. Tomando en cuenta la ecuación (2.10), en el modelo de la parte eléctrica del 138H MI en el MR fijo al estator, ecuación (2.5), se multiplica la ecuación de voltajes de 139H * Kirchhoff para el estator por is y la ecuación de voltajes de Kirchhoff para el rotor * por ir ´ , se obtiene la parte real de ambas ecuaciones (estator y rotor) y se multiplican por 3/2, obteniéndose: 29 Capítulo 2. Modelado del vehículo eléctrico 3 3 3 ⎛ dψ ⎞ Re ( us is * ) = Re ( Rs is is*) + Re ⎜ s is * ⎟ 2 2 2 ⎝ dt ⎠ 3 3 ⎛ dψ ´ ⎞ 3 0 = Re ( Rr ir ´ ir ´* ) + Re ⎜ r ir ´* ⎟ + Re ( − jωrψ r ´ir ´* ) 2 2 ⎝ dt ⎠ 2 (2.11) Analizando la ecuación (2.11) término por término, se tiene que: 140H • 3 Re ( us is * ) es la potencia de entrada, 2 • 3 Re ( Rs is is * ) es la potencia disipada en forma de calor en las 2 resistencias de los devanados del estator, • 3 ⎛ dψ s * ⎞ Re ⎜ is ⎟ es la derivada respecto al tiempo de la energía 2 ⎝ dt ⎠ magnética almacenada en los devanados del estator, • 3 Re ( Rr ir ´ ir ´* ) es la potencia disipada en forma de calor en las 2 resistencias de los devanados del rotor, • 3 ⎛ dψ r ´ * ⎞ Re ⎜ ir ´ ⎟ es la derivada respecto al tiempo de la energía 2 ⎝ dt ⎠ magnética almacenada en los devanados del rotor, y • 3 Re ( − jωrψ r ´ir ´* ) es la potencia mecánica de salida en la flecha del 2 motor, es decir, la potencia que se convierte de eléctrica en mecánica. A partir de este último término es posible obtener la expresión para el par que desarrolla el MI. Por otro lado, la potencia mecánica Pmec es igual al producto del par electromagnético te por la velocidad angular mecánica eléctrica con P pares de polos ωrm. Para una máquina θr = Pθrm, donde θr es la posición eléctrica del rotor y 30 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía θrm es la posición angular mecánica del rotor. Esta misma relación se cumple con la velocidad ωr = Pωrm, donde ωr es la velocidad eléctrica del rotor y ωrm es la velocidad mecánica del rotor. Considerando lo anterior se tiene: 3 Pmec = Re ( − jωrψ r ´ir ´* ) = teωrm 2 3 ω Pmec = − ωrψ r ´× ir ´= te r 2 P (2.12) Despejando el par electromagnético se tiene: 3 te = − P ψ r ´× ir ´ 2 (2.13) La expresión dada en (2.13) no es la única para calcular el par 14H electromagnético, existen varias y dependiendo de la aplicación una puede ser más adecuada que otra. Para encontrar la expresión utilizada en el control directo de par, es necesario considerar que de acuerdo con (2.6) 142H ψ s = Ls is + Lm ir ´ y ψ r ´= Lr ir ´+ Lm is , de aquí se puede obtener que ir ´= ( Ls / Ls ´Lr )ψ r ´− ( Lm / Ls ´Lr )ψ s , sustituyendo esta última expresión en (2.13), y considerando que 143H ψ r ´× ψ r ´= 0 , se obtiene: 3 L te = P m ψ r ´×ψ s 2 Ls ´Lr Lm 2 donde Ls ´= Ls − Lr 31 (2.14) Capítulo 2. Modelado del vehículo eléctrico Esta expresión para el par electromagnético es la que se utiliza en el control directo de par. Otra expresión para el par electromagnético que es útil, es la que se presenta en la ecuación (2.15), la cual puede obtenerse a partir de la ecuación (2.14) y las 14H 145H expresiones para los enlaces de flujo de la ecuación (2.6). 146H te = 2.4. 3 P ψ s × is 2 (2.15) Parte mecánica del VE Para el caso de un VE se puede considerar como carga mecánica del motor eléctrico al propio VE. La parte mecánica del VE se entenderá como el conjunto formado por: la transmisión, las ruedas, y la masa total de sus componentes (baterías, convertidores electrónicos, motor/generador eléctrico, transmisión, carrocería, chasis, etc.). En esta sección se obtiene la ecuación diferencial que modela la parte mecánica del VE. Como primera parte se considera el conjunto transmisión y neumáticos con entrada el par electromagnético desarrollado por motor y como salida la fuerza de tracción en los neumáticos. Si se considera una transmisión simple, representada en la figura 2.4, es necesario considerar las siguientes ecuaciones que modelan este tipo de transmisión: tL = r F η g G te (2.16) r Fte G (2.17) tL = η g 32 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía donde r es el radio del neumático en m, ηg es la eficiencia de la transmisión, G es el cociente de reducción de velocidad angular de la transmisión, tL es el par de entrada a la transmisión (par de carga del MI) en N·m y Fte es la fuerza de tracción que impulsa al VE. La ecuación (2.16) se utiliza cuando la máquina eléctrica entrega 147H potencia mecánica, es decir, funciona como motor (condiciones normales de operación) y la ecuación (2.17) se utiliza cuando la máquina eléctrica recibe potencia 148H mecánica, es decir, funciona como generador (frenado regenerativo). Motor G r Neumático Fte Figura 2.4. Representación de la transmisión del VE. Asimismo, de la figura 2.4 se puede obtener la relación entre la velocidad lineal v del VE y la velocidad angular ωrm del motor en rad/s. ωrm = G v r (2.18) Como segunda parte se obtendrá el modelo dinámico del VE considerando como entrada la fuerza de tracción Fte y como salida la velocidad lineal v del VE. La fuerza de tracción Fte es la que impulsa al VE, transmitida al suelo a través de los neumáticos. Para obtener el modelo de la parte mecánica del VE es necesario encontrar la ecuación diferencial que relaciona esta fuerza de tracción con la 33 Capítulo 2. Modelado del vehículo eléctrico velocidad del VE. Esta ecuación diferencial se obtiene aplicando la segunda Ley de Newton, para lo cual se identifican las fuerzas que actúan sobre el VE, las cuales se muestran en la figura 2.5 (Gao et al, 2007). Figura 2.5. Fuerzas actuantes sobre el VE en una pendiente. La fuerza de fricción Frr entre los neumáticos y la superficie sobre la cual se mueve el vehículo está dada por: Frr = μrr mg cos (φ ) sign(v) donde (2.19) μrr es el coeficiente de fricción, m es la masa total del vehículo en kg, g = 9.8 m/s2 es la aceleración debida a la gravedad, φ es el ángulo de inclinación de la pendiente, v es la velocidad lineal del VE en m/s y la función sign(v) está definida por: ⎧1 v>0 ⎪ sign ( v ) = ⎨ 0 v = 0 ⎪ ⎩−1 v < 0 La fuerza de fricción con el viento es: Fad = 12 ρ ACd v 2 34 (2.20) Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía ρ = 1.25 kg/m3 es la densidad del aire, A es el área frontal del VE en m2 y Cd donde es el coeficiente aerodinámico. La fuerza Fhc necesaria para mover el VE hacia arriba por la pendiente con un ángulo de inclinación φ, es una componente de su peso a lo largo de la pendiente, Fhc = mgsen (φ ) (2.21) Aplicando la segunda ley de Newton al VE: Fte − Frr − Fad − Fhc = ma (2.22) donde a es la aceleración del VE en m/s2 y Fte es la fuerza de tracción proporcionada por el motor eléctrico a través de la transmisión. Despejando Fte en (2.22) y sustituyendo (2.19), (2.20) y (2.21), se obtiene la 149H 150H 15H 152H ecuación diferencial que relaciona la Fte con la velocidad v. Fte = ma + μrr mgcos (φ ) sign(v) + 12 ρ ACd v 2 + mgsen (φ ) (2.23) En la ecuación (2.23) no se ha considerado el MI y la transmisión. Para esto 153H es necesario partir de la ecuación de pares: te = J donde: d ωrm + Bωrm + tL dt te es el par electromagnético generado por el motor. 35 (2.24) Capítulo 2. Modelado del vehículo eléctrico J es la inercia total (rotor y VE). B es el coeficiente de fricción viscosa. ωrm es la velocidad mecánica angular del rotor. tL es el par de la carga. La inercia total en el marco de referencia del motor es: J = J MI + JVE (2.25) donde JMI es el momento de inercia del MI y JVE es el momento de inercia del VE, este último está dado por: J VE 1 r2 = m 2 2 G (2.26) En este caso el par de carga del motor es el propio VE, por tanto, para el funcionamiento como motor es posible sustituir la ecuación (2.16) en (2.24). 154H te = J 15H d ωrm r + Bωrm + F η g G te dt (2.27) Por otra parte la Fte está dada en la ecuación (2.23) y puede sustituirse en 156H (2.27) para obtener: 157H te = J d ωrm r ⎛ dv + Bωrm + m + μrr mgcos (φ ) sign( v ) η g G ⎜⎝ dt dt ⎞ + 12 ρ ACd v 2 + mgsen (φ ) ⎟ ⎠ 36 (2.28) Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía En esta última ecuación se tiene tanto la velocidad angular mecánica del motor ωrm como la velocidad lineal v del VE, sin embargo (2.18) relaciona estas dos 158H velocidades. Dejando todo en función de la velocidad angular ωrm y despejando su derivada se obtiene el modelo de la parte mecánica del VE. ⎛ ηgG 2 μ mgrcos (φ ) sign( v ) d ωrm = te − Bωrm − rr 2 2 ⎜ dt Jη g G + mr ⎜⎝ ηgG − mgrsen (φ ) ⎞ ρ ACd r 2 − ω ⎟⎟ rm 2η g G 3 ηg G ⎠ (2.29) 3 Para el funcionamiento como generador (frenado regenerativo) se sigue un procedimiento similar obteniendo la siguiente ecuación: μrr mgη g rcos (φ ) sign( v ) ⎛ d ωrm G2 t B ω = − − ⎜ e rm dt JG 2 + mη g r 2 ⎝ G − ρ Aη g Cd r 2G 3 3 ωrm 2 − mgη g rsen (φ ) ⎞ ⎟⎟ G ⎠ (2.30) Por tanto el modelo de la parte mecánica del VE está dado por las ecuaciones (2.29) y (2.30). 159H 160H 2.5. Simulación del VE en lazo abierto Con las ecuaciones obtenidas en este capítulo, se realizaron las simulaciones del funcionamiento del VE. A continuación se presentan las simulaciones en lazo abierto del VE. La simulación del VE se realizó con el diagrama a bloques en simulink® mostrado en la figura 2.6. 37 Capítulo 2. Modelado del vehículo eléctrico Las simulaciones se realizaron bajo las siguientes condiciones: • Voltaje de CD constante (banco de baterías) de 300 V. • Modulación PWM senoidal, la cual consiste en comparar una señal de referencia a modular y una señal portadora de forma triangular; la comparación genera un tren de pulsos de ancho específico que se utilizan en la conmutación del inversor. Se utilizó una portadora de 1 V pico a una frecuencia de 10 kHz, y tres señales de referencia (moduladoras) senoidales de 0.95 V pico a 60 Hz desfasadas 120° entre ellas. • Los parámetros del VE se presentan en la tabla 2.1. • Los parámetros para el MI están dados en la tabla 2.2. Voltajes_estator Ias 300 Vcd Ibs Vas Van Vcd Ics + Vra - Out Ibr Comparador1 Vbs v bn Icr + Vrb - Out mb thr Portadora - Comparador3 wr Vcs Vcn Out corrientes_rotor wr Comparador2 + Vrc corrientes_estator Iar ma Te mc v Inversor MI 3f + VE Portadora1 thr Te v Figura 2.6. Diagrama a bloques en simulink® del VE. 38 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía Tabla 2.1. Parámetros del VE. Parámetro Valor Masa, m 1366 kg Coeficiente aerodinámico, Cd 0.23 Área frontal, A 2.66 m2 Coeficiente de fricción, μrr 0.015 Cociente de la transmisión, G 5.5 Eficiencia de la transmisión, ηg 0.95 Radio de los neumáticos, r 0.2876 m Parámetro Tabla 2.2. Parámetros del MI trifásico. Valor Potencia nominal 15 hp Voltaje de alimentación nominal 230 Vrms Corriente nominal 17.8 Arms Resistencia de estator, Rs 0.06336 Ω Resistencia de rotor, Rr 0.073558 Ω Inductancia de dispersión de estator, Lls 0.8646 mH Inductancia de dispersión de rotor, Llr 0.8646 mH Inductancia magnetización estator, Lms 17.913 mH Inductancia magnetización rotor, Lmr 17.913 mH Inductancia mutua estator-rotor, Lsr 17.913 mH Momento de inercia, JMI 1.0473 kg·m2 Coeficiente de fricción viscosa, B 11.5347x10-3 kg·m2/s Número de pares de polos, P 2 39 Capítulo 2. Modelado del vehículo eléctrico En la figura 2.7 se muestran los voltajes de fase del inversor que a su vez son los voltajes de alimentación del MI, el inciso d) muestra a detalle el voltaje de la fase a durante el periodo de 0 a 2.5 ms. 150 100 100 50 50 voltaje (V) 200 150 voltaje (V) 200 0 0 -50 -50 -100 -100 -150 -150 -200 0 0.005 0.01 0.015 0.02 0.025 0.03 tiempo (s) 0.035 0.04 0.045 -200 0.05 0 0.005 0.01 0.015 0.02 a) 0.025 0.03 tiempo (s) 0.035 0.04 0.045 0.05 b) 200 100 200 50 150 100 0 voltaje (V) voltaje (V) 150 -50 -100 50 0 -50 -100 -150 -200 -150 0 0.005 0.01 0.015 0.02 0.025 0.03 tiempo (s) 0.035 0.04 0.045 -200 0 0.05 0.5 1 1.5 2 tiempo (s) c) 2.5 -3 x 10 d) Figura 2.7. Voltajes de fase: a) van, b) vbn, c) vcn y d) acercamiento de van. Las corrientes del estator y rotor se muestran en las figuras 2.8 y 2.9 respectivamente haciendo un acercamiento para observar su comportamiento en estado estacionario. Tanto los voltajes como las corrientes forman un conjunto trifásico y balanceado, esto se puede apreciar más fácilmente en las corrientes. Las corrientes del estator en estado estacionario tienen una frecuencia fundamental de 60 Hz y otra componente de alta frecuencia (10 kHz) de la portadora. 40 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía 300 25 20 200 15 10 corriente (A) corriente (A) 100 0 -100 5 0 -5 -10 -15 -200 -20 -300 0 5 10 15 20 25 30 tiempo (s) 35 40 45 -25 49.95 49.955 49.96 49.965 49.97 49.975 49.98 49.985 49.99 49.995 tiempo (s) 50 a) 50 b) Figura 2.8. Corrientes del estator en el intervalo de a) 0 a 50s y b) 49.95 a 50s. 300 20 15 200 10 5 corriente (A) corriente (A) 100 0 -100 0 -5 -10 -200 -15 -300 0 5 10 15 20 25 30 tiempo (s) 35 40 45 -20 48 50 48.2 48.4 48.6 a) 48.8 49 49.2 tiempo (s) 49.4 49.6 49.8 50 b) Figura 2.9. Corrientes del rotor en el intervalo de a) 0 a 50s y b) 48 a 50s. En la figura 2.10 se muestra: a) el par desarrollado por el MI, b) la velocidad angular del MI, c) la velocidad lineal del VE y d) la potencia desarrollada por el MI. Se puede observar que el VE alcanza su estado estacionario después de los 40 s, con una velocidad de 9.78 m/s (aproximadamente 35.2 km/h). 41 Capítulo 2. Modelado del vehículo eléctrico 150 200 180 100 160 velocidad (rad/s) 140 par (Nm) 50 0 120 100 80 60 -50 40 20 -100 0 5 10 15 20 25 30 tiempo (s) 35 40 45 0 50 0 5 10 15 20 a) 35 40 45 50 35 40 45 50 b) 10 20000 9 18000 8 16000 7 14000 12000 6 potencia (W) velocidad (m/s) 25 30 tiempo (s) 5 4 10000 8000 6000 3 4000 2 2000 1 0 0 -2000 0 5 10 15 20 25 30 tiempo (s) 35 40 45 50 c) 0 5 10 15 20 25 30 tiempo (s) d) Figura 2.10. Variables mecánicas del VE: a)Par desarrollado por el MI, b) Velocidad angular del MI, c) Velocidad lineal del VE y d) Potencia desarrollada por el MI. 42 Capítulo 3. DISEÑO DEL CONTROLADOR El controlador utilizado en este trabajo se basa en el principio de funcionamiento del control directo de par (DTC por sus siglas en inglés Direct Torque Control). En el cual se controla el par electromagnético generado por el MI por medio de los enlaces de flujo del estator. En este capítulo primero se explica el principio del DTC convencional, haciendo énfasis en el proceso de generación del par electromagnético en un MI. Posteriormente, se presentan el controlador propuesto en este trabajo haciendo uso del análisis del fenómeno de la producción del par electromagnético del MI. El controlador propuesto toma en cuenta la ecuación diferencial que relaciona a los enlaces de flujo del estator con el voltaje aplicado al estator. Esto permite un mejor control de los enlaces de flujo del estator y por lo tanto del par electromagnético que el DTC convencional, el cual utiliza una tabla para generar los pulsos de conmutación del inversor. Además, con el esquema propuesto es posible utilizar PWM vectorial para generar los pulsos de conmutación del inversor, con lo que se logra una frecuencia de conmutación constante y una reducción de armónicos en las corrientes del estator. El DTC permite un control preciso y rápido del flujo y el par del MI. Esta estrategia de control se utiliza ampliamente en VE (Singh et al, 2006). En el DTC se 43 Capítulo 3. Diseño del controlador controla directa e independientemente el flujo y par por medio de la selección óptima de los modos de conmutación del inversor. Con este control se logra una rápida respuesta dinámica, una frecuencia de conmutación baja, y una reducción de armónicos (Bazzi et al, 2009). 3.1. Estimación de flujo y par Para poder implementar el DTC es necesario conocer el valor del flujo y el par. Debido a que las mediciones de estas variables no son simples y suele ser costoso el equipo para medirlas, se buscan otras alternativas tales como la estimación. Para el DTC es necesario estimar el módulo y ángulo del fasor espacial de enlaces de flujo del estator ψ s , además del par electromagnético te. La estimación se hace a partir de la ecuación (2.5) de voltajes del estator del motor de inducción en el 16H MR estacionario, la cual se repite a continuación: dψ s dt dψ ´ 0 = Rr ir ´+ r − jωrψ r ´ dt us = Rs is + (3.1) Despejando en (3.1) el fasor espacial de enlaces de flujo del estator (Faiz y 162H 58H Sharifian, 2001) se obtiene: 59H ψˆ s = ∫ ( us − Rs is ) dt (3.2) donde ψˆ s es el estimado del fasor espacial de enlaces de flujo del estator. Para realizar esta estimación se utilizan las mediciones de voltajes y corrientes en el 44 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía estator. El voltaje del estator se puede reconstruir a partir del valor del voltaje del bus de CD y de las señales de modulación, utilizando el modelo matemático del inversor. Tomando en cuenta que, para las corrientes isA + isB + isC = 0 , basta con la medición de dos fases. Esta estimación depende también de la resistencia del estator Rs. Algunos problemas que se pueden presentar al estimar el fasor de enlaces de flujo del estator utilizando la ecuación (3.2) son los siguientes: 163H • Errores en las mediciones de voltaje y/o corrientes del estator pueden ocasionar que el valor estimado sea erróneo. • Error en el valor de Rs ya que puede variar debido principalmente a la temperatura del devanado del estator. • La precisión de la técnica de integración influye directamente en la estimación. • El flujo puede tener un valor inicial desconocido lo que provoca un error de estimación que se arrastra a lo largo del tiempo. Los problemas anteriores se deben principalmente a que se trata de una técnica de estimación en lazo abierto, es decir, no se tiene retroalimentación para reducir el error de estimación. Una vez conocido (mediante estimación) el valor del fasor espacial de enlaces de flujo del estator, es posible obtener el par electromagnético estimado tˆe mediante la ecuación (2.15): 164H 3 tˆe = P ψˆ s × is 2 45 (3.3) Capítulo 3. Diseño del controlador La estimación del par también será imprecisa, si se tiene un error en la estimación de los enlaces de flujo del estator. 3.2. Control directo de par Para entender el DTC se parte de la ecuación (2.14) del par electromagnético, 165H expresando el par en función de los módulos ψ s y ψ r ´ y de los ángulos ρs y ρr, de los fasores espaciales de enlaces de flujo del estator y rotor, respectivamente. En la figura 3.1, se muestran los fasores espaciales involucrados en la producción del par. te = 3 L 3 L P m ψ r ´×ψ s = P m ψ r ´ ψ s sen ( ρ s − ρ r ) 2 Ls ´Lr 2 Ls ´Lr (3.4) La constante de tiempo del rotor de un MI tipo jaula de ardilla es grande en comparación con la constante de tiempo del estator (Vas, 1998), por tanto, el fasor espacial de enlaces de flujo del rotor cambia lentamente (comparado con el fasor espacial de enlaces de flujo del estator) y puede asumirse constante durante pequeños lapsos de tiempo. Por tanto el control del par se puede llevar a cabo mediante el fasor espacial de enlaces de flujo del estator. sQ ψs ρs ρ r′ ψ r′ sD Figura 3.1. Producción del par electromagnético. 46 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía A partir de (3.4) se puede observar que, si se mantiene constantes 16H ψs y ψ r ´ , el par puede cambiarse rápidamente mediante ρs – ρr. Por tanto, en DTC el fasor espacial de los enlaces de flujo del estator es la variable de control, a diferencia del control vectorial donde el control se realiza mediante las corrientes del estator. Así, en el DTC, el módulo ψ s controla la magnitud del flujo y el ángulo ρs controla el par. En el DTC un rápido control de par puede lograrse mediante la modificación de la posición del fasor espacial de los enlaces de flujo de estator relativa al fasor espacial de los enlaces de flujo del rotor, el cual se mueve lentamente. Por otra parte, el fasor espacial de los enlaces de flujo del estator (módulo y ángulo) se puede cambiar mediante el fasor espacial de voltaje del estator. Esto se puede ver a partir de la ecuación de voltajes del estator. us = Rs is + dψ s dt (3.5) Si se desprecia la caída de voltaje en las resistencias del estator ( Rs is = 0 ), us = dψ s dt Considerando un corto lapso de tiempo (3.6) Δt (el cual tiende a cero), durante el cual se aplica us , Δψ s = us Δt 47 (3.7) Capítulo 3. Diseño del controlador De esta última se observa claramente que el fasor espacial de enlaces de flujo del estator se puede cambiar directamente mediante el fasor espacial de voltaje del estator. En este trabajo, el voltaje del estator del MI se aplica mediante un inversor trifásico, este puede proporcionar seis fasores espaciales de voltaje activos y dos fasores espaciales de voltaje cero. El fasor espacial de voltaje del inversor está dado por: ⎧2 ⎪ V exp ⎡⎣ j ( k − 1 ) π / 3 ⎤⎦ u k = ⎨ 3 cd ⎪⎩ 0 k = 1, 2, 3, 4, 5, 6 (3.8) k = 0, 7 donde Vcd es el voltaje del bus de cd. Los fasores de voltaje del inversor se muestran en la figura 3.2. Los números entre paréntesis representan las señales de modulación del inversor Sa, Sb y Sc para cada fasor espacial de voltaje. También se muestra los seis sectores de π/3 rad en los que se divide el plano para el DTC convencional. u3 = (010) u2 = (110) Se cto r2 r3 cto Se u1 = (100) r6 cto Se u0 = (000) u7 = (111) Se cto r5 u4 = (011) u6 = (101) u5 = (001) Figura 3.2. Fasores espaciales de voltaje del inversor. 48 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía En la figura 3.3 se muestra un diagrama a bloques del DTC convencional. El subíndice ref indica los valores de referencia para las variables. El DTC utiliza dos comparadores: un comparador de histéresis de dos niveles para el error de flujo (figura 3.4.a) y un comparador de histéresis de tres niveles para el error de par (figura 3.4.b). Las bandas de tolerancia Δψ y Δte establecen los valores permisibles de error para el flujo y el par, respectivamente. Si la salida del comparador de flujo dψ es igual a uno es necesario incrementar el flujo, si en cambio la salida es cero es necesario reducir el flujo. Para el comparador de par, si su salida dte es: 1 es necesario incrementar el par, 0 no es necesario cambiar el par, –1 es necesario reducir el par. De acuerdo a la salida de los comparadores de flujo dψ y par dte, y al sector (ver figura 3.2) en la cual se encuentre el fasor espacial de enlaces de flujo del estator, es el valor que se envía a las señales de modulación del inversor Sa, Sb y Sc, de acuerdo con la tabla 3.1. tˆe ψ sref ψˆ s ρˆ s Figura 3.3. Diagrama a bloques del DTC convencional. 49 Capítulo 3. Diseño del controlador dψ dte 1 −Δψ 1 Δψ 0 −Δte 0 ψ sref − ψ s Δte teref − te -1 a) b) Figura 3.4. Comparadores de histéresis de: a) 2 niveles para el flujo y b) 3 niveles para el par. dψ 1 0 3.3. Tabla 3.1. Tabla de conmutación para el DTC. dte Sector 1 Sector 2 Sector 3 Sector 4 Sector 5 Sector 6 1 110 010 011 001 101 100 0 111 000 111 000 111 000 -1 101 100 110 010 011 001 1 010 011 001 101 100 110 0 000 111 000 111 000 111 -1 001 101 100 110 010 011 Controlador propuesto El controlador propuesto se basa en el principio de producción del par electromagnético descrito en la sección anterior, el cual establece que el control del par se puede llevar a cabo mediante el fasor espacial de enlaces de flujo del estator (Vas, 1998). Como se mencionó en la sección anterior, un rápido control de par puede lograrse mediante la modificación de la posición del fasor espacial de los enlaces de flujo de estator relativa al fasor espacial de los enlaces de flujo del rotor, el cual se mueve lentamente. 50 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía Así, el módulo ψ s del fasor espacial de enlaces de flujo del estator controla la magnitud de los enlaces de flujo y la derivada respecto al tiempo dρs/dt del ángulo del fasor espacial de enlaces de flujo del estator controla el par. Por tanto, el control del par y el flujo se puede realizar mediante el fasor espacial de enlaces de flujo del estator, y este a su vez puede ser modificado mediante el fasor de voltaje del estator. Para el diseño del controlador propuesto, se parte de la ecuación de voltajes del estator del MI tipo jaula de ardilla, en el MR estacionario: us = Rs is + dψ s dt (3.9) El fasor espacial de enlaces de flujo del estator se puede expresar en función de su módulo y su ángulo como: ψ s = ψ s e j ρs . Si se substituye esta última expresión en la ecuación (3.9), se obtiene: 167H us = Rs is + u s = Rs is + donde, la derivada del módulo ( d ψ s e j ρs ) dt d ψ s jρs d ρ s jρs e + jψs e dt dt d ψs dt y la derivada del ángulo (3.10) (3.11) d ρs del fasor dt espacial de enlaces de flujo del estator aparecen explícitamente. De aquí que, tanto el módulo como el ángulo del fasor espacial de enlaces de flujo del estator puedan ser modificados mediante el fasor espacial de voltaje del estator. 51 Capítulo 3. Diseño del controlador Analizando los términos del lado derecho de la ecuación (3.11), se tiene que: 168H 1. El primer término Rs is está relacionado con la caída de voltaje en los devanados del estator, por tanto al utilizar esta ecuación como base para el cálculo de la señal de control (fasor espacial de voltaje del estator) se realiza la compensación de esta caída. 2. El segundo término d ψ s jρs corresponde a la derivada respecto al tiempo e dt del módulo del fasor espacial de enlaces de flujo del estator en el MR fijo al estator. Para lograr el control del flujo, la derivada del módulo del fasor espacial de enlaces de flujo del estator se iguala al error de flujo eψ = ψ sref − ψ s multiplicado por la constante del controlador de flujo kψ, es decir, d ψs = kψ eψ dt (3.12) De la ecuación (3.12) se puede deducir que el módulo del fasor espacial de 169H enlaces de flujo del estator es igual a: ψ s = kψ ∫ eψ dt (3.13) Por lo que, este controlador es equivalente a un controlador integral que actúa directamente sobre el flujo. La ganancia kψ está estrechamente relacionada con la velocidad de respuesta del flujo magnético. 52 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía 3. Respecto al tercer término de la derecha de la ecuación (3.11), j ψ s 170H d ρ s jρs e . dt Se tiene que el par electromagnético desarrollado por el MI es proporcional al producto del módulo del fasor espacial de enlaces de flujo del estator y al cambio de su posición respecto al tiempo (Vas, 1998), es decir, te ∝ ψ s d ρs dt (3.14) donde el símbolo ∝ indica proporcionalidad. De esta última ecuación, se puede proponer el siguiente controlador de par, ψs d ρs = k1et + k2 ∫ et dt dt (3.15) donde k1 y k2 son respectivamente, las ganancias proporcional e integral del controlador de par, y et es el error de par definido como et = teref − te . La ecuación (3.15) es equivalente a un controlador proporcional–integral que 17H actúa directamente sobre el par desarrollado por el MI. Finalmente, substituyendo los controladores de flujo y par, ecuaciones (3.13) y 172H (3.15) respectivamente, en la ecuación (3.11); se obtiene un control directo de flujo y 173H 174H par con compensación de la caída de voltaje Rs is en los devanados del estator: ( ) us = Rs is + kψ eψ e j ρˆ s + j k1et + k2 ∫ et dt e j ρˆs 53 (3.16) Capítulo 3. Diseño del controlador En la figura 3.5 se muestra el diagrama a bloques del controlador propuesto, dado en la ecuación (3.16). Este difiere en cuanto al DTC principalmente en cuanto a 175H la forma en que se calcula el fasor espacial de voltaje del estator: en el caso del DTC convencional este se calcula mediante una tabla de conmutación (Bazzi et al, 2009), y en el controlador propuesto se calcula mediante la ecuación (3.16). Otra diferencia 176H es la forma en la cual las señales de conmutación (Sa, Sb y Sc) son generadas: en el DTC estas provienen directamente de la tabla de conmutación, y en el controlador propuesto se utiliza la técnica PWM vectorial (SVM, por sus siglas en inglés Space Vector Modulation); en el anexo 4 se aborda el tema del PWM vectorial. Por otra parte, en el controlador propuesto, a diferencia del DTC, no se utilizan comparadores de histéresis. tˆe ψ sref ψˆ s ρˆ s Figura 3.5. Diagrama a bloques del controlador propuesto. 3.4. Simulaciones En esta sección se presentan las simulaciones llevadas a cabo para evaluar el desempeño del DTC y del controlador propuesto. Para ambas simulaciones: • La carga del MI es el VE. 54 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía • Los parámetros para del VE y del MI están dados en las tablas 2.1 y 2.2 presentadas el capítulo anterior. • Se empleó un controlador PI para controlar la velocidad cuyas ganancias se obtuvieron de manera heurística kp = 5000 y ki = 300. • El perfil de velocidad deseada es el mismo para ambos controladores. • El par deseado es la salida del controlador PI de velocidad. • La magnitud de referencia del fasor espacial de los enlaces de flujo del estator (flujo deseado) se seleccionó constante e igual a 0.6 Wb·vuelta. • El flujo y el par se estimaron mediante las ecuaciones (3.2) y (3.3), 17H 178H respectivamente. • El voltaje del bus de cd es 300 V. 3.4.1. DTC convencional En la figura 3.6 se muestra el diagrama en Simulink® para el DTC. Los valores Δψ = 0.01 Wb·vuelta de las bandas de los comparadores de histéresis utilizados son y Δte = 2.5 N·m. Con estos valores se obtuvo una frecuencia de conmutación máxima de 18.2 kHz. Si se reducen las bandas de histéresis, la frecuencia de conmutación aumenta pudiendo superar el valor máximo soportado por los dispositivos de conmutación. flujo mag Va magnitud flujo Vb Vc sector [sector] ia ib par ic Estimador de flujo y par 0.6 300 Flujo deseado Comparador de histeresis Vcd Ias Vcd Van Ibs Vas Ics df ma ma PID dt mb mb sector mc mc Ibr Icr Vbs Controlador de Velocidad Velocidad deseada [te] [v] Comparador de histeresis 3 niveles [sector] Vcn wr thr Inversor Tabla de conmutacion corrientes _estator Iar vbn Te Vcs v [v] Fte MI + VE v te1 Figura 3.6. Diagrama del DTC convencional en Simulink®. 55 [te] Capítulo 3. Diseño del controlador La velocidad deseada, así como la velocidad desarrollada por el VE en simulación se muestran en la figura 3.7.a), en la figura 3.7.b) se tiene el error de velocidad (m/s) velocidad (m/s) velocidad el cual oscila entre –0.028 m/s y 0.012 m/s. 4 3 velocidad velocidad deseada 2 1 0 0 2 4 6 8 10 12 tiempo (s) a) 14 16 0.02 18 20 22 Error de velocidad 0.01 0 -0.01 -0.02 -0.03 0 2 4 6 8 10 12 tiempo (s) b) 14 16 18 20 22 Figura 3.7. a) Velocidad vs. velocidad deseada y b) error de velocidad. La salida del controlador PI de velocidad, es decir, el par deseado, y el par estimado se aprecian en la figura 3.8.a). El error de par presentado en la figura 3.8.b) no permanece todo el tiempo dentro de la banda de histéresis Δte = 2.5 N·m pues llega a tener valores cercanos a 3.5 N·m. El flujo estimado tiene un buen seguimiento respecto al flujo deseado (Figura 3.9) durante el intervalo de tiempo 1s < t < 21s. De 0 a 1 s el seguimiento de flujo no es bueno debido a que durante este tiempo el error de par es prácticamente cero y de acuerdo con la tabla 3.1 de la sección 3.2, cuando esto sucede no importa que exista error de flujo el voltaje del inversor es cero. Algo similar sucede en el último segundo de simulación. 56 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía par (Nm) 100 50 0 -50 -100 -150 0 Par estimado Par deseado 2 4 6 8 6 8 10 12 14 16 18 20 22 10 12 14 16 18 20 22 tiempo (s) a) par (Nm) 4 2 0 -2 -4 0 Error de par 2 4 tiempo (s) b) flujo (Wb vuelta) flujo (Wb vuelta) Figura 3.8. a) Par deseado vs. par estimado y b) error de par. 0.8 0.6 0.4 Flujo estimado Flujo deseado 0.2 0 0 2 4 6 8 10 12 tiempo (s) a) 14 16 0.6 18 20 22 Error de flujo 0.4 0.2 0 -0.2 0 2 4 6 8 10 12 tiempo (s) b) 14 16 18 20 Figura 3.9. a) Flujo deseado vs. estimado y b) error de flujo 57 22 Capítulo 3. Diseño del controlador La magnitud de las corrientes que circulan en los devanados del estator está estrechamente relacionada con el par electromagnético desarrollado, de aquí que su valor varíe a lo largo del tiempo de simulación como se muestra en la figura 3.10.a). Un acercamiento a las corrientes durante el intervalo de tiempo de 15 s a 15.1 se presenta en la figura 3.10.b). corriente (A) 200 isA 100 isB 0 isC -100 -200 0 2 4 6 8 10 12 tiempo (s) a) 14 16 18 20 corriente (A) 40 22 isA 20 isB 0 isC -20 -40 15 15.01 15.02 15.03 15.04 15.05 15.06 tiempo (s) b) 15.07 15.08 15.09 15.1 Figura 3.10. Corrientes del estator: a) 0 a 22s y b) 15s a 15.1s. En la figura 3.11 se presenta la trayectoria del fasor espacial de enlaces de flujo del estator, la cual idealmente debería de ser una circunferencia de radio 0.6 Wb·vuelta. Parte del origen y comienza a girar al tiempo que aumenta su magnitud. Como se mencionó anteriormente, su magnitud está relacionada con el flujo y su rotación con el par. 58 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía Trayectoria ψs 0.8 0.6 0.4 ψsQ (Wb vuelta) 0.2 0 -0.2 -0.4 -0.6 -0.8 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 ψ sD (Wb vuelta) Figura 3.11. Trayectoria del flujo del estator. 3.4.2. Controlador propuesto El diagrama en Simulink® para el controlador propuesto se presenta en la figura 3.12. La ganancia del controlador de flujo se fijo en kψ=100, para obtener un tiempo de levantamiento del flujo de 0.02 s., y las ganancias del controlador de par k1=14.76 y k2=885.6, se calcularon utilizando el método de Ziegler–Nichols. flujo mag Va magnitud flujo Vb Vc ang [ang ] par [te] ia ib ic Estimador de flujo y par Ias 0.6 300 Flujo deseado ef PID [ang ] Controldor de velocidad ma ma mb mb Ibr vbn [is] Icr Vbs wr rho mc is [te] Iar Van et [v] [is] Ics Vcd Vcd Velocidad deseada Ibs Vas mc Te Inversor CDP thr Vcn Vcs v [v] Fte MI + VE v te3 Figura 3.12. Diagrama del controlador propuesto en Simulink®. 59 Capítulo 3. Diseño del controlador En la figura 3.13 se presentan la velocidad deseada vs. velocidad desarrollada por el VE, así como el error de velocidad. La velocidad deseada es la misma que para el DTC convencional, así mismo la velocidad desarrollada por el VE y el error de velocidad son muy similares a los obtenidos en la simulación del DTC convencional (Figura 3.7), esto se debe a que el controlador de velocidad es el mismo para ambas velocidad (m/s) velocidad (m/s) simulaciones. 4 3 velocidad velocidad deseada 2 1 0 0 2 4 6 8 10 12 tiempo (s) a) 14 16 0.02 18 20 22 Error de velocidad 0 -0.02 -0.04 0 2 4 6 8 10 12 tiempo (s) b) 14 16 18 20 22 Figura 3.13. a) Velocidad deseada vs. velocidad y b) error de velocidad. La salida del controlador PI de velocidad, es decir, el par deseado y el par estimado se aprecian en la figura 3.14.a). El error de par presentado en la figura 3.14.b) es menor al obtenido en la simulación del DTC convencional. Para el controlador propuesto el error de par no supera 1.5 N·m mientras que para el DTC convencional este error llega a ser mayor de 3 N·m. Aunque para ambos controladores se tiene un seguimiento adecuado del par, el rizo de par es menor en el controlador propuesto. 60 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía par (Nm) 100 50 0 -50 -100 -150 0 Par estimado Par deseado 2 4 6 8 6 8 10 12 14 16 18 20 22 10 12 14 16 18 20 22 tiempo (s) a) par (Nm) 4 2 0 -2 -4 0 Error de par 2 4 tiempo (s) b) Figura 3.14. a) Par deseado vs. par estimado y b) error de par. Como se aprecia en la figura 3.15, el control de flujo también presenta mejor desempeño en el controlador propuesto que en el DTC convencional. El error de flujo, una vez pasado el transitorio, es muy pequeño, oscila entre –1.5x10–3 Wb·vuelta y 1.5x10–3 Wb·vuelta. Las corrientes del estator se presentan en la figura 3.16, su magnitud es muy similar a las obtenidas con el DTC convencional, sin embargo como se aprecia en la figura 3.16.b) su distorsión es mucho menor en el controlador propuesto. La magnitud de las corrientes en los devanados del estator está estrechamente relacionada con el par electromagnético desarrollado por el MI. De aquí que, su valor varíe a lo largo del tiempo de simulación. 61 flujo (Wb vuelta) Capítulo 3. Diseño del controlador 0.8 0.6 0.4 Flujo estimado Flujo deseado 0.2 0 0 2 4 6 8 10 12 tiempo (s) a) 14 16 flujo (Wb vuelta) 0.6 18 20 22 Error de flujo 0.4 0.2 0 -0.2 0 2 4 6 8 10 12 tiempo (s) b) 14 16 18 20 22 Figura 3.15. a) Flujo deseado vs. estimado y b) error de flujo. corriente (A) 200 isA 100 isB 0 isC -100 -200 0 2 4 6 8 10 12 tiempo (s) a) 14 16 18 20 corriente (A) 40 22 isA 20 isB 0 isC -20 -40 15 15.01 15.02 15.03 15.04 15.05 15.06 tiempo (s) b) 15.07 15.08 15.09 15.1 Figura 3.16. Corrientes del estator: a) 0 a 22s y b) 15s a 15.1s. 62 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía La trayectoria del fasor espacial de enlaces de flujo del estator se aproxima más a una circunferencia en el controlador propuesto, ver figura 3.17. Al igual que para el DTC convencional, parte del origen y comienza a girar al tiempo que aumenta su magnitud. Su magnitud está relacionada con el flujo y su rotación con el par. Trayectoria de ψs 0.8 0.6 0.4 ψ sQ (Wb vuelta) 0.2 0 -0.2 -0.4 -0.6 -0.8 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 ψsD (Wb vuelta) Figura 3.17. Trayectoria del flujo del estator. Con base en los resultados de simulación para los errores de par y flujo, distorsión en las corrientes del estator y trayectoria del flujo del estator; el desempeño del controlador propuesto es superior al desempeño del DTC convencional. 63 Capítulo 4. ALGORITMO DE SELECCIÓN DE FLUJO Comúnmente la magnitud de los enlaces de flujo magnético de referencia en un motor se elige de manera que se maximice el par electromagnético desarrollado no importando el consumo de energía. Sin embargo en un VE la magnitud de los enlaces de flujo debe ser elegida de manera distinta debido a que el aspecto de consumo de energía toma más importancia. Como se muestra en la figura 4.1 convencionalmente la magnitud de los enlaces de flujo magnético de referencia se elige de manera constante desde velocidad angular cero hasta la velocidad angular nominal ωn, después de este valor se reduce la magnitud de los enlaces de flujo magnético de manera inversamente proporcional a la velocidad para evitar la saturación magnética; a esta última zona se le conoce como debilitamiento de campo. El flujo magnético de referencia se puede elegir menor al flujo convencional con el objetivo de reducir el consumo de energía. Sin embargo, es necesario mantener un flujo magnético mínimo φmín para el correcto funcionamiento del motor, ya que si el flujo disminuye, también la amplitud del par disminuye dando como resultado un pobre desempeño dinámico (Faiz y Sharifian, 2001). Por tanto el flujo magnético deseado para el motor del VE debe de estar en la zona sombreada en la figura 4.1. 65 Capítulo 4. Algoritmo de selección de flujo Figura 4.1. Flujo magnético deseado vs. velocidad angular. Las técnicas de optimización para motores eléctricos se pueden subdividir en dos grandes grupos: búsqueda del punto óptimo y usando un modelo de pérdidas. Para la técnica basada en la búsqueda del punto óptimo, no es necesario contar con el modelo de pérdidas para realizar la optimización. Su funcionamiento se basa en medir la potencia de entrada durante un intervalo de tiempo, mientras busca el valor del flujo óptimo el cual dé cómo resultado la mínima potencia de entrada. Para llevar a cabo esta técnica es necesario que la potencia de salida permanezca constante durante el intervalo de tiempo que dura la búsqueda, es decir, se necesita que el producto del par y la velocidad angular sea constante. Esta condición de potencia de salida constante es prácticamente imposible de mantener en un VE, debido a constantes cambios de velocidad y par que se requieren. Se encuentra reportada en varios trabajos la técnica basada en la búsqueda de control óptimo (Li et al, 2005), (Bose et al, 1997), (Kioskesidis y Margaris, 1996), (Moreno-Eguilaz et al, 1997) y (Sundareswaran y Palani, 1999) pero ninguno de ellos aplicado a VE. Algunas ventajas de esta técnica son: • Si la potencia de entrada es medida directamente en la batería, la optimización no está restringida al motor. • No depende de los parámetros del motor. 66 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía La técnica de optimización basada en el modelo de pérdidas del motor se basa en la medición de velocidad (o par) y las corrientes del estator, y determinar el flujo magnético óptimo a través del modelo del motor. El modelo del motor empleado para determinar el flujo magnético contiene parámetros del motor como inductancias y resistencias. Esta técnica es más adecuada para VE, pero tiene el inconveniente de depender de parámetros del motor los cuales pueden tener variaciones. Las inductancias pueden variar debido a la saturación magnética, pero esta se evita limitando el flujo magnético para que permanezca por debajo del flujo magnético convencional (ver figura 4.1). La variación en las resistencias se debe a la temperatura, sin embargo estas variaciones permanecen acotadas. Algunos trabajos que han utilizado esta técnica basada en modelo de pérdidas son: (Raj, 2006), (Wang y Qiu, 2005), (Pryymak et al, 2006), (Hamid et al, 2006), (ElLaben, 2006), (Cao et al, 2006), (Tsouvalas et al, 2007), (Perron y Huy, 2006), (Haddoun et al, 2007), (Dilmi y Yurkovich, 2005). Algunas ventajas de esta técnica son: • No es necesario mantener la potencia de salida en un valor constante. • No existe retardo en el cálculo del flujo óptimo. La técnica basada en el modelo de pérdidas del motor se eligió para seleccionar el flujo de referencia en este trabajo por ser más adecuada para VE. Por tanto, para desarrollar el algoritmo de selección de flujo magnético para reducir las pérdidas eléctricas en el VE, es necesario conocer el modelo de pérdidas del VE y posteriormente buscar la forma de reducir dichas pérdidas. El primer paso para encontrar el modelo de pérdidas es analizar el modelo de cada una de las partes del VE e identificar las pérdidas que se presentan en cada una de ellas. 67 Capítulo 4. Algoritmo de selección de flujo 4.1. Análisis de la eficiencia La eficiencia η de un dispositivo se define como la relación entre la potencia de salida Po y la potencia de entrada Pi. Asimismo, la potencia de salida se puede expresar como la potencia de entrada menos las pérdidas totales PT. O bien, la potencia de entrada se puede expresar como la potencia de salida más las pérdidas totales. η= Po Pi − PT Po = = Pi Pi Po + PT (4.1) La potencia de salida en un VE es igual al producto de la velocidad lineal v y la fuerza de tracción Fte en los neumáticos. Po = v ⋅ Fte (4.2) Por otra parte la potencia de entrada del VE se obtiene mediante el producto del voltaje en terminales del banco de baterías Vcd y la corriente que entregan las baterías Icd. Pi = Vcd ⋅ I cd (4.3) De (4.1) se puede deducir que, una forma de elevar la eficiencia es reduciendo 179H las pérdidas totales, esto sin afectar la potencia de salida. En este trabajo se propone elegir el flujo magnético de referencia de manera que se reduzcan las pérdidas. Por tanto, es necesario primero analizar las pérdidas que se presentan en el VE. 68 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía 4.2. Modelo de pérdidas En la figura 4.2 se presenta el circuito equivalente del MI (Fitzgerald et al, 2003), el cual es útil para hacer un análisis de las pérdidas que se presentan en este. Rs y R’r son las resistencias del estator y del rotor referida al estator, respectivamente. Ls, L’r y Lm son las inductancias del estator, del rotor referida al estator y de magnetización, respectivamente. Is, I’r e Ic son las corrientes del estator, del rotor referida al estator y del núcleo, respectivamente. ωs es la frecuencia angular del estator y s es el deslizamiento del MI. ⎛ 1− s ⎞ ⎜ ⎟ ⎝ s ⎠ Figura 4.2. Circuito equivalente del MI. Con el objeto de simplificar el análisis de las pérdidas en el MI se utiliza una transformación de tres a dos fases en el MR fijo al fasor espacial de enlaces de flujo del estator, con lo cual la corriente del estator tiene dos componentes en cuadratura: isx llamada componente de flujo magnético e isy que es la componente del par electromagnético, como se muestra en la figura 4.3 (Haddoun et al, 2007). ⎛ 1− s ⎞ ⎜ ⎟ ⎝ s ⎠ Figura 4.3. Circuito equivalente alternativo del MI. 69 Capítulo 4. Algoritmo de selección de flujo Las diferentes pérdidas que se presentan en el MI, cuyo circuito equivalente se muestra en la figura 4.3, son las siguientes: • en el cobre del estator: Ps = Rs I s 2 = Rs ( isx 2 + isy 2 ) • • (4.4) en el cobre del rotor: Pr = Rr′ I r′2 = Rr′isy 2 (4.5) Pm = K mωr 2 (4.6) mecánicas: Debido a que las pérdidas mecánicas sólo dependen de la velocidad y no del flujo magnético, estas no tienen influencia en la selección del flujo de referencia. Por lo tanto, por el momento no se consideran dentro de las pérdidas totales. 4.3. Algoritmo de selección de flujo Las pérdidas dadas en las ecuaciones (4.4) y (4.5) se pueden reacomodar de 180H 18H la siguiente forma: • • en el eje x: Px = Rsisx 2 (4.7) Py = [ Rs + Rr′ ] isy 2 (4.8) en el eje y: El par electromagnético te se puede expresar en función de las componentes isx e isy de la corriente del estator: 70 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía te = 3 PLmisxisy 2 (4.9) Usando (4.9) las pérdidas totales PT, el cual es resultado de la suma de (4.7) y 182H 183H (4.8) se puede expresar como: 184H PT = isy 2te ⎛ isx ⎜⎜ Rs + [ Rs + Rr′ ] isx 3PLm ⎝ isy ⎞ ⎟⎟ ⎠ (4.10) Esta última función es la que se pretende minimizar mediante la elección del flujo magnético del MI. Con objeto de minimizar (4.10), es posible usar la variable 185H auxiliar A definida por: isx isy (4.11) 2te ⎛ 1⎞ ⎜ Rs A + [ Rs + Rr′ ] ⎟ 3PLm ⎝ A⎠ (4.12) A= Con lo cual se obtiene: PT = Obteniendo la derivada parcial de esta última respecto a la variable auxiliar A e igualando a cero: 71 Capítulo 4. Algoritmo de selección de flujo ∂PT =0 ∂A 2te ⎛ 1 ⎞ ⎜ Rs − [ Rs + Rr′ ] 2 ⎟ = 0 A ⎠ 3PLm ⎝ Rs = [ Rs + Rr′ ] (4.13) 1 A2 Sustituyendo la variable auxiliar A en (4.13) se obtiene: 186H Rs = [ Rs + Rr′ ] Rsisx 2 isy 2 isx 2 = [ Rs + Rr′ ] isy 2 (4.14) De (4.14) se puede observar que el lado izquierdo de la igualdad es igual a las 187H pérdidas en el eje x, ecuación (4.7), y el lado derecho es igual a las pérdidas en el 18H eje y, ecuación (4.8). Por lo tanto: 189H Px = Py (4.15) De aquí se deduce que para minimizar las pérdidas es necesario que las pérdidas en el eje x y en el eje y sean iguales. Dado que la componente isy está relacionada con el par electromagnético desarrollado por el MI y este debe seguir a la referencia fijada por el pedal del acelerador, la única opción para poder hacer iguales estás pérdidas (Px y Py) es variar la componente isx la cual está relacionada con el flujo magnético. En la figura 4.4 se muestra un diagrama a bloques del algoritmo de selección de flujo, el cual funciona de la siguiente manera: 72 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía 1. El bloque “Modelo de pérdidas” calcula las potencias Px y Px usando el modelo de pérdidas dado por las ecuaciones (4.7) y (4.8), a partir de las 190H 19H componentes de la corriente del estator isx e isy. 2. Para lograr que estas potencias sean iguales se utiliza un controlador PI. Si Px < Py se aumenta el flujo magnético de referencia (el cual está relacionado con ix y por lo tanto con Px). Si Px > Py se disminuye el flujo magnético de referencia. 3. Posteriormente se limita la salida del controlador PI para que el flujo de referencia esté dentro de la zona de operación del MI (área sombreada de la Figura 4.1). ψ sref Figura 4.4. Algoritmo de selección de flujo. 4.4. Simulación Para analizar el uso de la energía en el VE se realizaron simulaciones en Matlab/Simulink®, utilizando el controlador propuesto presentado en el capítulo anterior. Las simulaciones se llevaron a cabo bajo las siguientes condiciones: • La carga del MI es el VE. • La frecuencia de conmutación de los interruptores que forman el inversor igual a 18 kHz. • El perfil de velocidad deseada es el mismo para todas las simulaciones, ver figura 4.5. En el cual se pueden apreciar 3 etapas claramente definidas: 73 Capítulo 4. Algoritmo de selección de flujo aceleración (0.5 a 4.5 s), velocidad constante (4.5 a 11.5 s) y frenado (11.5 a 15.5 s). • Se realizaron distintas simulaciones con diferentes valores de flujo deseado: o Para flujo magnético fijo desde 0.45 hasta 1.15 Wb·vuelta. o Para flujo magnético variable, utilizando el algoritmo de selección de flujo descrito en la sección anterior. 4 3.5 velocidad (m/s) 3 2.5 2 1.5 1 0.5 0 0 2 4 6 8 tiempo (s) 10 12 14 16 Figura 4.5. Velocidad de referencia para el VE. A continuación se presentan los resultados para un flujo de referencia variable utilizando el algoritmo de selección de flujo de la sección anterior. La velocidad deseada, así como la velocidad desarrollada por el VE en simulación se muestran en la figura 4.6.a), mientras que en la figura 4.6.b) se tiene el error de velocidad el cual oscila entre ±0.027 m/s. La salida del controlador PI de velocidad, es decir, el par deseado, y el par estimado se aprecian en la figura 4.7.a). El error de par es presentado en la figura 4.7.b) el cual oscila entre – 0.4 N·m y 3.4 N·m. 74 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía 0.03 velocidad velocidad deseada 4.5 4 Error de velocidad 0.02 3.5 0.01 velocidad (m/s) velocidad (m/s) 3 2.5 2 1.5 0 -0.01 1 0.5 -0.02 0 -0.5 0 2 4 6 8 tiempo (s) 10 12 14 -0.03 0 16 2 4 6 8 10 tiempo (s) 12 14 16 a) b) Figura 4.6. a) Velocidad deseada vs. velocidad y b) error de velocidad. 4 Par estimado Par deseado 100 3 50 2 par (Nm) par (Nm) 150 0 1 -50 0 -100 -1 -150 0 2 4 6 8 tiempo (s) 10 12 14 16 Error de par -2 0 2 4 6 8 tiempo (s) 10 12 14 16 a) b) Figura 4.7. a) Par deseado vs. par estimado y b) error de par. El flujo de referencia (deseado) es la salida del algoritmo de selección de flujo. Teniendo como limite inferior 0.45 Wb·vuelta y superior 1.1 Wb·vuelta. El flujo estimado tiene un buen seguimiento respecto al flujo deseado, ver figura 4.8.a). El error de flujo, una vez pasado el transitorio, es muy pequeño, oscila entre –5x10–3 Wb·vuelta y 6.5x10–3 Wb·vuelta como se observa en la figura 4.8.b). 75 Capítulo 4. Algoritmo de selección de flujo La magnitud de las corrientes que circulan en los devanados del estator está estrechamente relacionada con el par electromagnético desarrollado y con el flujo magnético producido, de aquí que su valor varíe a lo largo del tiempo de simulación como se muestra en la figura 4.9.a). Un acercamiento a las corrientes durante el intervalo de tiempo de 8 a 8.1 s se presenta en la figura 4.9.b). -3 8 x 10 Error de flujo 6 1 0.8 flujo (Wb vuelta) flujo (W b vuelta) 4 0.6 0.4 2 0 -2 -4 0.2 -6 Flujo estimado Flujo deseado 0 0 2 4 6 8 tiempo (s) 10 12 14 -8 0 16 2 4 6 8 tiempo (s) 10 12 14 a) b) Figura 4.8. a) Flujo deseado vs. flujo estimado y b) error de flujo. isA 150 isA 30 isB isB isC 100 20 50 10 corriente (A) corriente (A) isC 0 0 -50 -10 -100 -20 -30 -150 0 2 4 6 8 tiempo (s) 10 12 14 16 8 8.01 8.02 8.03 8.04 8.05 8.06 tiempo (s) 8.07 a) b) Figura 4.9. Corrientes del estator: a) 0 a 16s y b) 8 a 8.1 s. 76 8.08 8.09 8.1 16 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía En la figura 4.10 se muestra la potencia de conversión de eléctrica a mecánica pconv ( t ) = teωrm , es decir, el producto del par desarrollado por el motor por la velocidad angular del motor. Cuando se tienen valores positivos indica una conversión de eléctrica a mecánica, en cambio cuando toma valores negativos indica una conversión de mecánica a eléctrica. Se observa que tanto durante la aceleración (0.5 a 4.5 s) como a velocidad constante la potencia desarrollada es positiva (4.5 a 11.5 s), en cambio durante el frenado (11.5 a 15.5 s), la potencia es negativa, es decir se tiene frenado regenerativo. Cabe recordar que en el frenado regenerativo la energía cinética (mecánica del VE) se recupera en forma de energía eléctrica. 4 x 10 Potencia de conversión 1 0.8 0.6 potencia (W) 0.4 0.2 0 -0.2 -0.4 -0.6 -0.8 -1 0 2 4 6 8 tiempo (s) 10 12 14 16 Figura 4.10. Potencia de conversión. Además de esta simulación utilizando un flujo variable (algoritmo de selección de flujo), se reprodujo está simulación para distintos valores de flujo magnético de referencia fijos desde 0.45 hasta 1.15. En la siguiente tabla se presentan las energías: de entrada, disipada en la parte eléctrica, convertida de eléctrica a mecánica, disipada en la parte mecánica y la entregada al VE, todas ellas calculadas mediante simulación para el mismo ciclo de conducción (figura 4.5) y para el valor del flujo de referencia indicado. Así mismo se calculó la relación entre la energía de entrada y la energía de salida. El 77 Capítulo 4. Algoritmo de selección de flujo Tabla 4.1. Análisis de energía en el VE. Energía mecánica disipada (J) Energía de entrada (J) Energía eléctrica disipada (J) 0.45 28,435.68 19,021.69 9,413.99 617.45 8,796.54 0.3093 0.50 23,883.02 14,469.06 9,413.96 617.44 8,796.52 0.3683 0.60 19,387.57 9,973.66 9,413.91 617.43 8,796.48 0.4537 0.70 17,182.64 7,768.76 9,413.88 617.43 8,796.45 0.5119 0.80 15,998.52 6,584.69 9,413.83 617.43 8,796.40 0.5498 0.90 15,437.95 6,024.20 9,413.75 617.42 8,796.33 0.5698 1.00 15,237.47 5,823.83 9,413.64 617.40 8,796.24 0.5773 1.10 15,264.45 5,851.07 9,413.38 617.37 8,796.01 0.5762 1.15 15,423.90 6,012.94 9,410.96 617.01 8,793.95 0.5702 Variable 13,468.67 4,054.85 9,413.82 617.43 8,796.39 0.6031 Flujo de referencia (Wb·vuelta) Energía convertida (J) Energía de salida (J) E. Salida / E. Entrada Cuando el flujo de referencia se mantuvo fijo se obtuvo un desempeño adecuado para los valores de aproximadamente 0.45 a 1.15 Wb·vuelta. Por tanto para el flujo variable la simulación se limitó este mismo rango. En la figura 4.11 se muestra una gráfica del flujo de referencia vs. la relación Energía de salida/Energía de entrada para el rango mencionado. E. salida/E. entrada 0.55 0.5 0.45 0.4 0.35 0.3 0.5 0.6 0.7 0.8 0.9 1 flujo de referencia (Wb vuelta) 1.1 Figura 4.11. Flujo de referencia vs. la relación Energía de salida/Energía de entrada. 78 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía Para valores fuera de este rango (0.45 a 1.15 Wb·vuelta) el desempeño del controlador no fue el adecuado. Por ejemplo en las figura 4.12 y 4.13 se presentan el seguimiento de velocidad y par para los flujos de referencia 0.4 y 1.2 Wb·vuelta. Se observa que no es posible desarrollar el par demandado y por tanto no se puede alcanzar la velocidad deseada. 4 4.5 4 x 10 Par estimado Par deseado 3 3.5 2.5 3 2 par (Nm) velocidad (m/s) 3.5 Velocidad Velocidad deseada 2.5 2 1.5 1 1.5 0.5 1 0 0.5 0 0 2 4 6 8 tiempo (s) 10 12 14 -0.5 0 16 2 4 6 8 tiempo (s) 10 12 14 16 b) a) Figura 4.12. a) Velocidad deseada vs. velocidad, b) par deseado vs. par estimado con flujo de referencia 0.4 Wb·vuelta. 4.5 600 Velocidad Velocidad deseada 4 400 3 300 par (Nm) velocidad (m/s) 3.5 2.5 2 200 100 1.5 1 0 0.5 -100 0 0 Par estimado Par deseado 500 2 4 6 8 tiempo (s) 10 12 14 -200 0 16 2 4 a) 6 8 tiempo (s) 10 12 14 16 b) Figura 4.13. a) Velocidad deseada vs. velocidad, b) par deseado vs. par estimado con flujo de referencia 1.2 Wb·vuelta. 79 Capítulo 5. IMPLEMENTACIÓN. CONTROL VOLTS/HERTZ La velocidad de un MI trifásico tipo jaula de ardilla puede ser controlada fácilmente mediante la variación de la frecuencia del voltaje trifásico aplicado al estator. Sin embargo, para mantener constante el flujo magnético, la amplitud del voltaje aplicado debe ser cambiada en la misma proporción que la frecuencia. Este método de control es conocido como Volts/Hertz (Krause et al, 2002), (Ong, 1998). Arriba de la velocidad base, la amplitud del voltaje aplicado se mantiene constante para evitar la saturación magnética, este modo de operación es conocido como potencia constante. A bajas frecuencias, la amplitud del voltaje debe mantener un valor mínimo para compensar los efectos de la caída de voltaje en la resistencia del estator. La curva Volts/Hertz empleada en la implementación del control en lazo abierto y del control en lazo cerrado se muestra en la figura 5.1, en el eje de la abscisas se tiene la frecuencia en Hz y en el eje de las ordenadas se tiene la amplitud del voltaje trifásico normalizada. 81 Capítulo 5. Implementación. Control volts/hertz 1 0.9 0.8 Voltaje normalizado 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0 0 10 20 30 40 50 60 frecuencia (Hz) 70 80 90 100 Figura 5.1. Relación Frecuencia – Voltaje. En la figura 5.2, se presenta el diagrama a bloques de la implementación del control Volts/Hertz, tanto en lazo abierto como en lazo cerrado. Para la implementación se utilizó el equipo mencionado en la tabla 5.1. Figura 5.2. Diagrama a bloques de la implementación del control Volts/Hertz. La fuente de CD variable ajustada a 150 V proporciona el voltaje del bus de CD para el inversor trifásico, este a su vez proporciona el voltaje trifásico al MI. Para medir la posición se tiene un encoder de tipo incremental y con base en esta 82 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía medición se calcula mediante el DSP la velocidad angular a la cual gira el MI. En el DSP se ejecuta el algoritmo de control, que calcula las 3 señales PWM vectorial y sus complementos para los disparos de las compuertas de los IGBTs que conforman el inversor. La laptop se usa con 2 objetivos: el primero de ellos es mediante el software Vissim© (Visual Solutions, 2010) programar el algoritmo de control y descargarlo al DSP, y el segundo es monitorear la velocidad angular del MI y otras variables de interés. Debido a que el voltaje trifásico se aplica al MI por medio de un inversor, este no es una señal senoidal pura, es decir, contiene armónicos de alta frecuencia debidos al proceso de modulación (PWM vectorial en este caso). Por tanto, en este documento cuando se haga referencia a la frecuencia del voltaje de alimentación se está hablando de la frecuencia fundamental. Tabla 5.1. Equipo utilizado para el control Volts/Hertz. Equipo Marca – Modelo Especificaciones Fuente de CD variable Sorensen 0 – 300 V, 0 – 16 A DCR 300-16T Inversor trifásico Motor de Powerex 800 V máximo, 300 A PP300T120 máximo inducción Baldor trifásico ZDNM3581T Encoder incremental BEI 1 HP, 230 V, 60 Hz 1024 Pulsos revolución DSP Texas Instruments TMS320F28335 83 32 bits, 150 MHz por Capítulo 5. Implementación. Control volts/hertz En la medición de la posición angular mediante el encoder incremental se presentó un problema de ruido, lo que dio lugar a errores en las mediciones y por tanto errores en el cálculo de la velocidad angular. En la figura 5.3, se muestran las señales del encoder, en a) el MI se encuentra detenido, y en b) está girando a una velocidad aproximada de 93.5 rad/s (892.86 rpm). Como se observa existe un ruido principalmente en una de las señales. a) b) Figura 5.3. Señales del encoder a: a) 0 rad/s, y b) 93.5 rad/s. 5.1. Control Volts/Hertz en lazo abierto. En esta sección se describe la implementación de un control de velocidad en lazo abierto para el MI, basado en la metodología de Volts/Hertz. Para la implementación del control Volts/Hertz en lazo abierto no se retroalimenta la velocidad medida. Simplemente se calcula la frecuencia de alimentación a partir de una velocidad de referencia dada, usando la siguiente fórmula: f = P ωrm 2π 84 (5.1) Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía donde f es la frecuencia en Hz, P es el número de pares de polos del MI (en este caso 2) y ωrm es la velocidad angular en rad/s. Una vez conocida la frecuencia, se calcula la amplitud del voltaje usando la gráfica de la figura 5.1. Y se aplica al MI mediante el inversor el voltaje trifásico de la frecuencia y amplitud calculadas. En la figura 5.4 se muestra el diagrama a bloques con el que se programó el DSP F28335 para el control Volts/Hertz en lazo abierto usando el software Vissim©. F28335 eQEP2 ref 0.318309886 *[email protected] convert QPOSCNT2(32.32) dir(16.16) QE(8.32) QEP Speed dir(32.32) Calculator32 Wr(8.32) 314.1592654 w Rev s(16.16) freq convert *[email protected] freq %Duty Cy cle A(1.16) f req(8.32) freq f req(8.32) Volts/Hertz v out(8.32) Profile32 v a(8.32) Space Vector Generator32 v b(8.32) gain(8.32) (Magnitude/Frequency) v c(8.32) scale scale scale F28335-EPWM1A/EPWM1 B F28335-EPWM3A/EPWM3 %Duty Cy cle B(1.16) B %Duty Cy cle A(1.16) F28335-EPWM2A/EPWM2 %Duty Cy cle B(1.16) B %Duty Cy cle B(1.16) %Duty Cy cle A(1.16) Vc © Figura 5.4. Diagrama a bloques en Vissim del control Volts/Hertz en lazo abierto. En la parte superior de la figura 5.4, se encuentra la lectura del encoder realizada mediante el bloque “F28335 eQEP2”, posteriormente, con ayuda del bloque “QEP Speed Calculator32”, se calcula la velocidad a partir de la posición obtenida. Cabe aclarar que la velocidad sólo se monitorea con el objetivo de observar el desempeño del controlador, ya que la velocidad medida no se utiliza para el cálculo de la señal de control, es decir, no existe retroalimentación. En la parte media del diagrama de la figura 5.4, únicamente se realiza la conversión de la referencia dada en rad/s a su equivalente en Hz, usando la ecuación (5.1). 192H En la parte inferior de la figura 5.4, se realiza el cálculo de la amplitud del voltaje a partir de la frecuencia mediante el bloque “Volts/Hertz Profile32” haciendo 85 Capítulo 5. Implementación. Control volts/hertz uso de la gráfica presentada en la figura 5.1. Posteriormente el bloque “Space Vector Generator32” hace el cálculo del ciclo de trabajo de las 3 señales PWM vectorial y estas se envían por las salidas digitales del DSP mediante los bloques “F28335EPWM1A/EPWM1B”, “F28335-EPWM2A/EPWM2B” y “F28335-EPWM3A/EPWM3B”. Los resultados de la implementación del control Volts/Hertz en lazo abierto se muestran en las figuras 5.5 y 5.6. En la figura 5.5 se presenta en a) la velocidad deseada y la velocidad medida, el perfil de velocidad de referencia se seleccionó pensando un VE teniendo tres etapas: aceleración (0 a 20 s), velocidad constante (20 a 30 s) y frenado (30 a 60 s). En b) se presenta el error de velocidad, cabe señalar que aproximadamente a los 58 s existe un error de medición de la velocidad debido al ruido de las señales del encoder, es por esto que el error se dispara en este instante de tiempo. 40 200 velocidad deseada velocidad medida 30 velocidad angular (rad/s) 150 velocidad angular (rad/s) Error de velocidad 35 100 50 25 20 15 10 5 0 0 -50 0 10 20 30 tiempo (s) 40 50 -5 0 60 a) 10 20 30 tiempo (s) 40 50 60 b) Figura 5.5. a) Velocidad deseada vs. velocidad medida, y b) error de velocidad. En la figura 5.6 se presenta en a) la frecuencia, que como se mencionó anteriormente se calcula con base en la velocidad de referencia haciendo uso de la ecuación (5.1), al estar en lazo abierto está frecuencia no depende de la velocidad 193H 86 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía medida. En b) se presenta la amplitud normalizada del voltaje, que se obtiene directamente de la frecuencia mediante la relación Volts/Hertz (ver figura 5.1). 1 60 Frecuencia Amplitud normalizada 0.9 0.8 50 0.7 voltaje normalizado frecuencia (Hz) 40 30 20 0.6 0.5 0.4 0.3 0.2 10 0.1 0 0 10 20 30 tiempo (s) 40 50 0 0 60 10 20 30 tiempo (s) 40 50 60 b) a) Figura 5.6. a) Frecuencia, y b) amplitud normalizada del voltaje trifásico aplicado. 5.2. Control Volts/Hertz en lazo cerrado. Para el control Volts/Hertz en lazo cerrado se retroalimenta la medición de la velocidad y se compara con la velocidad de referencia para obtener la señal de error. Esta señal de error es la entrada de un controlador PI, cuya salida es la frecuencia del voltaje trifásico. La ecuación que se usa para el controlador PI es la siguiente: f = k p e + ki ∫ e dt (5.2) donde f es la frecuencia del voltaje trifásico aplicado al MI, e es el error de velocidad, es decir, la diferencia entre la velocidad de referencia y la velocidad medida, kp y ki son las ganancias proporcional e integral respectivamente. 87 Capítulo 5. Implementación. Control volts/hertz En este caso, las ganancias del controlador PI se eligieron de manera heurística los siguiente valores kp = 0.09 y ki = 0.0075. Al igual que en el control Volts/Hertz en lazo abierto, la amplitud normalizada del voltaje se obtiene por medio de la relación Frecuencia – Voltaje (Figura 5.1). En la figura 5.7 se muestra el diagrama a bloques con el que se programó el DSP F28335 para el control Volts/Hertz en lazo cerrado usando el software Vissim©. F28335 eQEP2 *[email protected] convert QPOSCNT2(32.32) dir(16.16) QE(8.32) QEP Speed dir(32.32) Calculator32 314.1592654 Wr(8.32) speed w Rev s(16.16) ref 315 ref 3.174603175e-3 3.174603175e-3 speed convert convert cmd(8.32) f eedback(8.32) PID32(0.09,0.0075,0) out(8.32) freq *[email protected] convert *[email protected] freq Va %Duty Cy cle A(1.16) f req(8.32) freq Volts/Hertz f req(8.32) v out(8.32) Profile32 v a(8.32) Space Vector Generator32 v b(8.32) gain(8.32) (Magnitude/Frequency) v c(8.32) scale scale scale F28335-EPWM1A/EPWM1 B F28335-EPWM3A/EPWM3 %Duty Cy cle B(1.16) B %Duty Cy cle A(1.16) F28335-EPWM2A/EPWM2 %Duty Cy cle B(1.16) B %Duty Cy cle B(1.16) %Duty Cy cle A(1.16) Figura 5.7. Diagrama a bloques en Vissim© del control Volts/Hertz en lazo cerrado. En la parte superior de la figura 5.7, se encuentra la lectura del encoder realizada mediante el bloque “F28335 eQEP2”, posteriormente, con ayuda del bloque “QEP Speed Calculator32”, se calcula la velocidad a partir de la posición obtenida. Esta velocidad es almacenada en la variable “Speed” para posteriormente restarla a la referencia y obtener el error de velocidad. 88 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía En la parte media del diagrama de la figura 5.7, se calcula la frecuencia del voltaje trifásico mediante el controlador PI programado en el bloque “PID32(0.09,0.0075,0)”, las entradas de este controlador son la velocidad deseada y la velocidad medida. En esta parte se da la principal diferencia con el diagrama del control Volts/Hertz en lazo abierto (Figura 5.4), en la forma como se calcula la frecuencia. En el control en lazo abierto esta se calcula mediante la ecuación (5.1) y 194H depende únicamente de la velocidad de referencia; en cambio en el control en lazo cerrado se usa un controlador PI cuya entrada es el error de velocidad. En la parte inferior de la figura 5.7, se realiza el cálculo de la amplitud del voltaje a partir de la frecuencia mediante el bloque “Volts/Hertz Profile32”. Posteriormente el bloque “Space Vector Generator32” hace el cálculo del ciclo de trabajo de las 3 señales PWM vectorial y estas se envían por las salidas digitales del DSP mediante los bloques “F28335-EPWM1A/EPWM1B”, “F28335- EPWM2A/EPWM2B” y “F28335-EPWM3A/EPWM3B”. Los resultados de la implementación del control Volts/Hertz en lazo cerrado se muestran en las figuras 5.8 y 5.9. En la figura 5.8 se presenta en a) la velocidad deseada y la velocidad medida, el perfil de velocidad de referencia usado, es el mismo que para el control en lazo abierto, consta de tres etapas: aceleración (0 a 20 s), velocidad constante (20 a 30 s) y frenado (30 a 60 s). En b) se presenta el error de velocidad, donde se presenta un “error de medición” de velocidad aproximadamente a los 27s debido al ruido de las señales del encoder. Sin tomar en cuenta el error debido al ruido en la medición de velocidad, el error para el control en lazo cerrado es menor que el obtenido para el control en lazo abierto. 89 Capítulo 5. Implementación. Control volts/hertz 200 40 velocidad deseada velocidad medida 30 velocidad angular (rad/s) velocidad angular (rad/s) 150 100 50 0 -50 0 Error de velocidad 20 10 0 -10 10 20 30 tiempo (s) 40 50 -20 0 60 10 20 a) 30 tiempo (s) 40 50 60 b) Figura 5.8. a) Velocidad deseada vs. velocidad medida, y b) error de velocidad. En la figura 5.9 se presenta en a) la frecuencia, que es la salida del controlador PI, al segundo 27 se observa como el controlador responde a la caída de la velocidad aumentado la frecuencia. En b) se presenta la amplitud normalizada del voltaje, en el segundo 27 aumenta junto con la frecuencia, sin embargo, al aumentar la frecuencia por encima de los 60 Hz el voltaje ya no aumenta y se mantiene en 0.9 (ver figura 5.1). 70 1 Frecuencia Amplitud normalizada 0.9 60 0.8 50 voltaje normalizado frecuencia (Hz) 0.7 40 30 20 0.5 0.4 0.3 10 0 0 0.6 0.2 0.1 10 20 30 tiempo (s) 40 50 60 0 0 a) 10 20 30 tiempo (s) 40 50 60 b) Figura 5.9. a) Frecuencia, y b) amplitud normalizada del voltaje trifásico aplicado. 90 Capítulo 6. CONCLUSIONES Los vehículos de combustión interna se han usado por muchos años como principal medio de transporte terrestre, sin embargo, tienen algunos inconvenientes que motivan a buscar nuevas alternativas. Los VE son una buena opción debido a que son más eficientes que los vehículos convencionales, no contaminan y su fuente de energía es muy flexible. Sin embargo los VE tienen el principal problema de contar con una cantidad de energía limitada. Debido a ello se debe hacer un uso eficiente de la energía disponible, con el objeto de aumentar su autonomía. Con el objetivo de imitar la operación del vehículo de combustión interna, en un VE es preferible tener un control de par, en lugar de un control preciso de velocidad en lazo cerrado. Es importante hacer un VE lo más parecido en cuanto a su conducción a un vehículo convencional. El uso de fasores espaciales para modelar el convertidor CD – CA (inversor) y el MI trifásico tipo jaula de ardilla simplifica su representación y análisis, comparado con la representación matricial que necesita más espacio. Además, esta representación es muy útil cuando se utiliza DTC. 91 Capítulo 6. Conclusiones El controlador directo de par convencional representa una buena opción para realizar control de par del VE, es sencillo de implementar y presenta una rápida respuesta y un buen desempeño dinámico. Sin embargo presenta algunos inconvenientes: un elevado rizo de par, la frecuencia de conmutación del inversor no es fija. El tener una frecuencia de conmutación variable puede ocasionar que no se aproveche al máximo la capacidad de los dispositivos semiconductores que forman el inversor, o bien que se sobrepase la frecuencia máxima de operación de dichos dispositivos. El estimador del fasor espacial de enlaces de flujo del estator usado comúnmente en el DTC, tiene entre otros inconvenientes el utilizar un integrador puro. Esto ocasiona problemas debidos a valor inicial y de deriva. Con base en el principio del DTC, se tiene que el control del par y flujo se puede llevar a cabo mediante el fasor espacial de enlaces de flujo del estator. Considerando que su movimiento es circular, si se actúa sobre su componente “radial” se afectará su modulo, es decir, el flujo; en cambio si se actúa sobre su componente “tangencial” se modificará su ángulo y a la vez el par. Por otra parte el fasor espacial de enlaces de flujo del estator se puede modificar directamente mediante el fasor espacial de voltaje del estator. Por medio de un análisis de la ecuación de voltajes del estator y del proceso de producción del par se encontró una ley de control que calcula el voltaje aplicado al estator a partir de los errores de par y flujo. En el controlador propuesto se trabaja en el MR fijo al fasor espacial de enlaces de flujo del estator. La componente usx del fasor espacial de voltaje del estator es proporcional al error de flujo, y la componente usy es proporcional al error de par. 92 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía El desempeño obtenido por el controlador propuesto es superior al del DTC convencional, bajo las mismas condiciones de simulación. Algunas características a destacar son: un bajo rizo de par, menor distorsión de las corrientes del estator y menores errores de par y flujo. El tener un rizo de par elevado aunque puede no ser perceptible en la velocidad del VE, sin embargo, este rizo puede afectar los componentes del VE. Es claro que el control del par es importante en VE, sin embargo también existe la necesidad de controlar el flujo magnético, la elección del valor deseado de este flujo puede ser fundamental en el consumo de energía. De la energía que se obtiene del banco de baterías una parte se disipa en forma de calor en el devanado del estator y otra parte se convierte en energía magnética. Esta energía magnética traspasa el entrehierro, es decir, pasa del estator al rotor, donde una parte se disipa en la resistencia del rotor y otra parte se convierte en energía mecánica. Una vez convertida en energía mecánica todavía existe disipación por fricción con los rodamientos y con el viento en el VE. De las potencias disipadas en el VE, es posible tratar de disminuir las pérdidas en los devanados del estator y del rotor mediante una elección adecuada del flujo magnético. Existen básicamente dos formas de hacer esto: por un proceso de búsqueda y basado en un modelo. En VE se utiliza el enfoque basado en modelo debido a que para aplicar el otro enfoque es necesario mantener la potencia de salida constante por un cierto tiempo, lo cual no es posible en el VE. El flujo magnético se puede modificar dentro de un rango sin afectar el desempeño del VE, sin embargo, este cambio en el flujo magnético si afecta el consumo de energía del banco de baterías. 93 Capítulo 6. Conclusiones Debido a que la disipación en la parte mecánica está en función principalmente de la velocidad y el par, no es posible disminuir esta disipación sin afectar el desempeño del VE. La técnica de control Volts/Hertz es la más simple para motores de inducción trifásico, sin embargo tiene el inconveniente de tener un pobre desempeño en lazo cerrado. Su funcionamiento se basa en mantener constante la relación voltaje – frecuencia en un cierto rango, y a bajas frecuencia y altas frecuencia mantener la amplitud del voltaje constante. Como era de esperarse el desempeño del controlador en lazo cerrado es superior al del control en lazo abierto, teniendo un menor error de velocidad. Esto debe ser más evidente al colocar carga mecánica al MI, ya que en las pruebas realizadas hasta el momento el motor ha operado en vacío. Debido a la alta frecuencia que se utiliza en las señales PWM vectorial, se puede inducir fácilmente ruido en otras partes del circuito. En este caso el ruido representa un problema al estar presente en las señales provenientes del encoder incremental, con el cual se calcula la posición y velocidad angular. En el control en lazo cerrado el ruido afecta la señal de control, y ocasiona que la oscilación de la velocidad sea mayor, esto debido a que el controlador al querer compensar la supuesta “caída” de velocidad en el MI aumenta la frecuencia, ocasionando que la velocidad se eleve y posteriormente regrese a su valor deseado. 94 Referencias Affanni et al, 2005 Bazzi et al, 2009 Blaschke, 1972 Bose et al, 1997 Bose, 1986 Cao et al, 2006 Chapman, 1999 Conae, 2002 Crompton, 2002 Depenbrock, 1985 Dilmi y Yurkovich, 2005 Affanni, A.; Bellini, A.; Franceschini, G.; Guglielmi, P.; Tassoni, C.; Battery Choice and Management for NewGeneration Electric Vehicles. IEEE Trans. on Industrial Electronics, Vol. 52, No. 5, Oct. 2005, pp. 1343-1349 A. M. Bazzi, A. P. Friedl, S. Choi, P. T. Krein, “Comparison of induction motor drives for electric vehicle applications: Dynamic performance and parameter sensitivity analyses,” IEEE International Electric Machines and Drives Conference, IEMDC 09, pp. 639 – 646, 2009. F. Blaschke, “The Principal of Field-Orientation as Applied to the New Transvektor Closed-Loop Control System for RotatingField Machines,” Siemens Review XXXIX, pp. 217-219, 1972. B. K. Bose, N. R. Patel, K. Rajashekra, “A neuro-fuzzy base online efficiency optimization control of a stator flux oriented direct vector controller induction motor drive, ” IEEE Trans. Ind. Electron., vol. 44, pp. 270-273, 1997. B. K. Bose, Power Electronics and AC Drives, Ed. Prentice-Hall, 1986 C. Cao, B. Zhou, M. Li, J. Du, “Digital implementation of DTC based on PSO for induction Motors,” IEEE Conf. Proc. Intelligent Control and Automation, pp. 6349-6352, 2006. S. J. Chapman, Electric machinery fundamentals. 3rd ed. McGraw-Hill series in electrical and computer engineering. 1999. Ficha Técnica: Vehículo Eléctrico, Comisión Nacional para el Ahorro de Energía México, www.conae.gob.mx, 2002 Crompton, T. R.; Battery Reference Book. Third Edition, Ed. Newnes, 2002. M. Depenhrock, “Direkte Selbstregelung (DSR) fiir hochdynamische Drehfeld-antriebe mit Stromrichterschaltung,” ETZ A 7, pp. 211-18, 1985. S. Dilmi, S. Yurkovich, “Nonlinear Torque Control of the Induction Motor in Hybrid Electric Vehicle Applications,” Proceedings of the American Control Conference, vol. 5, pp. 3001 – 3006. 2005. O.S. El-Laben, “Particle Swarm Optimized direct torque control of Induction Motor,” IEEE Conf. Proc. IECON, pp. 1586-1591, 2006. 60H El-Laben, 2006 95 Referencias Emadi, 2005 Faiz et al, 2002 Faiz et al, 2003 Faiz y Sharifian, 2001 Ferrerira et al, 2008 Fitzgerald et al, 2003 Gao et al, 2007 Guillespie, 1992 Haddoun et al, 2007 Emadi, A.; Handbook of Automotive Power Electronics and Motor Drives. CRC Press, 2005 J. Faiz, M. B. B. Sharifian, A. Keyhani, A. B. Proca, “Sensorless Direct Torque Control of Induction Motors Used in Electric Vehicle,” IEEE Power Engineering Review, vol. 22, pp: 54 – 55, 2002. J. Faiz, M. B. B. Sharifian, A. Keyhani, A. B. Proca, “Sensorless direct torque control of induction motors used in electric vehicle,” IEEE Transaction on Energy Conversion, vol. 18, pp. 1 – 10, 2003 J. Faiz, M. B. B. Sharifian, “Different techniques for real time estimation of an induction motor rotor resistance in sensorless direct torque control for electric vehicle,” IEEE Transaction on Energy Conversion, vol. 16, pp. 104 – 109, 2001. Ferreira, A.; Pomilio, J.; Spiazzi, G.; Silva, L.; “Energy Management Fuzzy Logic Supervisory for Electric Vehicle Power Supplies System”, IEEE Transactions on Power Electronics, Vol. 23, No. 1, January 2008, pp. 107-115 A. E. Fitzgerald, C. Kingsley, S.D. Umans, Electric machinery. 6th ed. McGraw-Hill series in electrical engineering. Power and energy, 2003. D. W. Gao, C. Mi, A. Emadi, “Modeling and Simulation of Electric and Hybrid Vehicles,” Proceedings of the IEEE, vol. 95, no. 4, pp. 729-745, 2007. Gillespie, T.; Fundamentals of vehicle dynamics, SAE International, 1992 A. Haddoun, M. E. H. Benbouzid, D. Diallo, R. Abdessemed, J. Ghouili, K. Srairi, “A Loss-Minimization DTC Scheme for EV Induction Motors,” IEEE Transactions on Vehicular Technology, vol. 56, pp. 81 – 88, 2007. R. H. A. Hamid, A. M. A. Amin, R. S. Ahmed, A. El-Gammal, “New technique for maximum efficiency of induction motors based on PSO,” IEEE conference proceedings, pp. 2176-2181, 2006. E. Hassankhan, D. A. Khaburi, “DTC-SVM Scheme for Induction Motors Fed with a Three-level Inverter,” World Academy of Science, Engineering and Technology, pp. 168 – 172, 2008 D. G. Homes, T. A. Lipo, Pulse Width Modulation For Power Converters. Principles and Practice. IEEE Press, 2003. P. F. Huerta González, J. J. Rodríguez Rivas, I. C. Torres Rodríguez, “Estimación de la resistencia del rotor usando una red neuronal artificial en el control vectorial indirecto del motor de inducción,” IEEE LATIN America Transactions, vol. 6, no. 2, pp 176 – 183, 2008. Husain, I.; Electric and Hybrid Vehicles, Design Fundamentals. CRC Press, 2003 61H 62H 63H 64H 65H 6H 67H 68H 69H 70H 71H 75H 72H 73H 74H 76H 7H Hamid et al, 2006 Hassankhan y Khaburi, 2008 Homes y Lipo, 2003 Huerta González et al, 2008 Husain, 2003 96 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía Idris et al, 2006 Jian et al, 2008 N. R. N. Idris, C. L. Toh, M. Elbuluk, “A New Torque and Flux Controllers for Direct Torque Control of Induction Machines,” IEEE Transactions on Industry Applications, vol. 42, no. 6, 2006. Z. Jian, W. Xuhu, H. Yang, “A novel speed-sensorless vector control technique of induction motor for electrical vehicle propulsion,” IEEE Vehicle Power and Propulsion Conference, VPPC 08, pp. 1 – 5, 2008. S. Jianguo, C. Quanshi, “Research of Electric Vehicle IM Controller Based On Space Vector Modulation Direct Torque Control,” Proceedings of the Eighth International Conference on Electrical Machines and Systems, ICEMS 2005, vol. 2, pp. 1617 – 1620, 2005. A. D. Karlis, K. Kiriakopoulos, D. P. Papadopoulos, E. L. Bibeau, “Comparison of the Field Oriented and Direct Torque Control Methods for Induction Motors used in Electric Vehicles,” XVII International Conference on Electrical Machines, 2006. F. Khoucha, K. Marouani, A. Haddoun, A. Kheloui, M. E. H. Benbouzid, “An Improved Sensorless DTC Scheme for EV Induction Motors,” IEEE International Electric Machines & Drives Conference, IEMDC '07. vol. 2 pp. 1159 – 1164, 2007. Kim, P.; Cost Modeling of Battery Electric Vehicle and Hybrid Electric Vehicle based on Mayor Parts Cost. International Conference on Power Electronics and Drive Systems, Nov. 2003. Kioskesidis, N. Margaris, “Loss minimization in scalar controlled induction motor drives with search controller,” IEEE Trans. Power Electronics, Vol. 11, No. 2, pp. 213-220, 1996. P. C. Krause, O. Wasynczuk, S. D. Sudhoff, Analysis of Electric Machinery and Drive Systems. IEEE Press, 2002. Larminie, J.; Lowry, J.; Electric Vehicle Technology Explained. John Wiley & Sons Ltd, 2003 Larminie, J.; Lowry, J.; Electric Vehicle Technology Explained. John Wiley & Sons Ltd, 2003 J. Li, L. Xu, Z, Zhang, “A new efficiency optimization method on vector control of induction motor, ” in Proc. IEEE Conf. Electrical Machines and Drives, pp. 1995-2001, 2005. H. Liu, Y. Zhou, Y. Jiang, L. Liu, T. Wang, B. Zhong, “Induction motor drive based on vector control for electric vehicles,” Proceedings of the Eighth International Conference on Electrical Machines and Systems, ICEMS 2005, vol. 1, pp. 861 – 865, 2005. H. Liu, Y. Zhou, Y. Jiang, L. Liu, T. Wang, B. Zhong, “Induction motor drive based on vector control for electric vehicles,” Proceedings of the Eighth International Conference on Electrical Machines and Systems, ICEMS 2005, vol. 1, pp. 861 – 865, 2005. Jianguo y Quanshi, 2005 Karlis et al, 2006 78H Khoucha et al, 2007 80H 79H 81H 84H Kim, 2003 Kioskesidis y Margaris, 1996 Krause et al, 2002 Larminie y Lowry, 2003 Larminie y Lowry, 2003 Li et al, 2005 Liu et al, 2005 Liu et al, 2005 97 82H 83H Referencias Moreno-Eguilaz et al, 1997 Ong, 1998 J. Moreno-Eguilaz, M. Cipolla, J. Peracaula, P. J. da Costa Branco, “Induction motor optimum flux search algorithms with transient state loss minimization using fuzzy logic based supervisor, ” IEEE Conf. Proc. 1997, pp. 1302-1308, 1997. C. M. Ong, Dynamic Simulation of Electric Machinery. Prentice Hall, 1998. Ortúzar, M.; Moreno, J.; Dixon, J.; Ultracapacitor-Based Auxiliary Energy System for an Electric Vehicle: Implementation and Evaluation. IEEE Transactions on Industrial Electronics, Vol. 54, No. 4, Aug. 2007 M. A. Ouhrouche, N. Léchevin, S. Abourida, “RT-Lab Based Real-Time Simulation of a Direct Field-Oriented Controller for an Induction Motor,” Proceedings of the 7th International Conference on Modeling and Simulation of Electric Machines, Converters and Systems, 2002. M. Ouhrouche, R. Beguenane, A. M. Trzynadlowski, J. S. Thongam, M. Dube-Dallaire, “A PC-Cluster Based Fully Digital Real-Time Simulation of a Field Oriented Speed Controller for an Induction Motor,” International Journal of Modelling and Simulation, pp. 1 – 20, 2003. M. Perron, H. L. Huy, “Full load range neural network efficiency optimization of an induction motor with vector control using discontinuous PWM, ” in Proc. IEEE Symp. Ind. Electron., vol.1, pp. 166-170, 2006. P. J. Pinewski, “Implementing A Simple Vector Controller,” Proceedings of the American Control Conference, 1997. B. Pryymak, J. M. Moreno-Eguilaz, J. Peracaula, “Neural network flux optimization using a model of losses in induction motor drives,” Mathematics and Computers in Simulation, Vol. 71, pp. 290-298, 2006. C. Thanga Raj, “Improving energy efficiency in partial loaded induction motor-using power electronic controllers, ” J. Engineering and Technology, Vol. 1, No. 2, pp. 13-17, 2006. Rajamani, R.; Vehicle Dynamics and Control, Springer, 2006 B. Singh, P. Jain, A. P. Mittal, J. R. P. Gupta, “Direct torque control: a practical approach to electric vehicle,” IEEE Power India Conference, 2006. K. Sundareswaran, S. Palani, “Fuzzy logic approach for energy efficient voltage controlled induction motor drive,” IEEE Power Electronics and Drives Conf. Proc. PEDS 1999, pp. 552-554, 1999. C.–M. Ta, Y. Hori, “Convergence Improvement of EfficiencyOptimization Control of Induction Motor Drive,” IEEE Transactions on Industry Applications, vol. 37, no. 6, pp. 1746 – 1753, 2001. Takahashi, T. Noguchi, “A new quick-response and high efficiency control strategy of an induction motor,” IEEE Trans. Ind. Appl., vol. IA-22, no. 5, pp. 820–827, 1986. Ortúzar et al, 2007 Ouhrouche et al, 2002 Ouhrouche et al, 2003 Perron y Huy, 2006 Pinewski, 1997 Pryymak et al, 2006 Raj, 2006 Rajamani, 2006 Singh et al, 2006 Sundareswaran y Palani, 1999 Ta y Hori, 2001 Takahashi y Noguchi, 1986 85H 86H 87H 98 8H Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía Trounce et al, 2001 Trzynadlowski, 2001 Tsouvalas et al, 2007 Vas, 1993 Vas, 1998 Vasudevan y Arumugam, 2004 Visual Solutions, 2010 Wang y Qiu, 2005 Wang y Stuart, 2002 Wu et al, 2008 Yi y Kaiqi, 2005 Zeraouila et al, 2005 J. C. Trounce, S. Round, R. Duke, “Evaluation of Direct Torque Control Using Space Vector Modulation for Electric Vehicle Applications,”. Australasian Universities Power Engineering Conference, pp. 292-297, 2001. A. M. Trzynadlowski, Control of Induction Motors. Academic Press, 2001. N. Tsouvalas, L. Xydis, L. Tsakirakis, Z. Papazacharopoulos, “Asynchronous motor drive loss optimization,” Material Processing and Technology, vol. 181, pp. 301-306, 2007. P, Vas, Electrical machines and drives: A space vector theory approach. Oxford, 1993. P. Vas, Sensorless Vector and Direct Torque Control. Oxford University Press, 1998. M. Vasudevan, R. Arumugam, “Simulation of Viable Torque Control Schemes of Induction Motor for Electric Vehicles,” 5th Asian Control Conference, vol. 2, pp. 1377 – 1383, 2004. VisSim/Embedded Controls Developer User's Guide Version 8.0, Visual Solution, Inc., 2010. Fang Wang, Yuhui Qiu, “A modified particle swarm optimizer with Roulette selection operator,” IEEE conference proceedings of NLP-E, pp. 765-768, 2005. Wang, X.; Stuart, T.; Charge Measurement Circuit for Electric Vehicle Batteries. IEEE Transactions on Aerospace and Electronic Systems, Vol 38, No. 4, Oct. 2002, pp. 1201-1209 J. Wu, D. Gao, X. Zhao, Q. Lu, “An efficiency optimization strategy of induction motors for electric vehicles,” IEEE Vehicle Power and Propulsion Conference, VPPC '08, 2008. W. Yi, Z. Kaiqi, “Field-oriented vector control of induction motor for electric vehicles,” 31st Annual Conference of IEEE Industrial Electronics Society, IECON 2005, 2005. M. Zeraouila, M. E. H. Benbouzid, D. Diallo, “Electric motor drive selection issues for HEV propulsion systems: a comparative study,” IEEE Conference Vehicle Power and Propulsion, 2005. 99 Anexo 1. TIPOS DE BATERÍAS EMPLEADAS EN VE Entre los medios de almacenamiento de energía empleados en VE se encuentran: las baterías, los ultracapacitores y los volantes de inercia. Estos medios de almacenamiento se pueden usar uno solo a la vez o se puede hacer la combinación de dos de ellos para obtener mejores resultados. Uno de los medios de almacenamiento de energía más ampliamente usado en VE son las baterías (Ortúzar et al, 2007). Los principales tipos de baterías utilizadas en VE son: Plomo-Ácido, NíquelCadmio (NiCd), Níquel-Metal hidrido (NiMH) e ion Litio (Li-ion) (Wang y Stuart, 2002). Adicionalmente existen baterías especialmente desarrolladas para su uso en VE, el ejemplo más claro son las llamadas ZEBRA por las siglas en inglés de “Zero Emissions Battery Research Association” (Larminie y Lowry, 2003). Las principales especificaciones que describen el desempeño de una batería son las siguientes: • Capacidad. Es la máxima carga que puede almacenar y se expresa en Ampere-hora (Ah). Este valor cambia de una batería a otra y decrece a lo largo de la vida de la batería. Sin embargo la carga que puede entregar la batería disminuye con el incremento de la corriente de descarga. Por lo cual 101 Anexo 1. Tipos de baterías empleadas en VE usualmente se especifica además de la capacidad (C), el tiempo de descarga nominal. Una forma de modelar la capacidad de las baterías es mediante la siguiente fórmula, llamada capacidad “Peukert” (Larminie y Lowry, 2003): C p = I kT (A1.3) donde Cp es una constante igual a la capacidad C a una corriente de descarga de 1 A, k es el coeficiente Peukert, I es la corriente en A, T es el tiempo de descarga en horas. • Energía Almacenada. Esta depende del voltaje de la batería y de su capacidad. En el SI su unidad es el Joule (J), sin embargo es común utilizar Watt-hora (Wh) como unidad de medida en sistemas eléctricos (1 Wh = 3600 J). Una forma de calcular la energía que puede almacenar una batería es la siguiente: Energía en Wh = V ⋅ C (A1.4) donde V es el voltaje de la batería en V y C es su capacidad en Ah. Sin embargo hay que tener cuidado al emplear esta ecuación ya que el voltaje de la batería y sobre todo su capacidad varían considerablemente dependiendo del uso que se haga de la batería. • Energía específica. Es la cantidad de energía eléctrica almacenada por cada kilogramo (kg) de batería. Sus unidades son Wh/kg. Una vez que se conoce la energía eléctrica almacenada por una batería, dada por la ecuación (A1.4), 195H esta se divide por la masa de la batería para obtener la energía específica. 102 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía • Densidad de energía. Es la cantidad de energía eléctrica almacenada por metro cúbico (m3) de volumen de la batería. Sus unidades son Wh/m3. • Potencia específica. Es la cantidad de potencia eléctrica obtenida por kilogramo de batería. Sus unidades son W/kg. Es una cantidad altamente variable debido a que la potencia entregada por la batería depende en gran medida de la carga conectada. Aunque las baterías tienen una potencia máxima sólo es posible demandar esta por unos cuantos segundos. La mayoría de las baterías tienen buena energía específica pero baja potencia específica, lo que significa que pueden almacenar mucha energía pero pueden entregarla lentamente. En la tabla A1.1 se presenta un resumen de las principales especificaciones de las distintas baterías empleadas en VE (Larminie y Lowry, 2003). Tabla A1.1. Especificaciones de los distintos tipos de baterías. Tipo de batería Energía Potencia Resistencia Temp. De Otras Propiedades específica específica interna (W) operación (°C) (Wh/kg) (W/kg) ~0.022 por celda ~0.06 por celda ~0.06 por celda Ambiente • Bajo costo –40 a 80 • Disponible sólo en tamaños pequeños Ambiente • • 150 Muy baja 300 – 350 • Disponible sólo en tamaños pequeños En grandes tamaños requieren de ventilación Pocos proveedores 300 Muy baja Ambiente • Plomo-ácido 20–35 ~250 INCD 40–55 ~125 NiMH ~65 200 ZEBRA 100 Li-ion 90 Disponible únicamente en tamaños pequeños Las baterías son uno de los componentes más críticos de un VE, ya que de estas depende el desempeño del VE sobre todo en el rango de operación (o autonomía), que es uno de los problemas que se tienen actualmente en VE. La 103 Anexo 1. Tipos de baterías empleadas en VE autonomía en un VE es la distancia en kilómetros que puede recorrer sin necesidad de recargar sus baterías. Las baterías han mejorado notablemente su desempeño en los últimos años, y se espera sigan mejorando. Sin embargo, sus energías específicas son todavía bajas. Las baterías más ampliamente utilizada en VE son las de plomo-ácido debido principalmente a su bajo costo y a su gran disponibilidad en el mercado, aunque estas se pueden emplear solamente en vehículos con poca autonomía. Baterías como NiMH, Li-ion y Zebra tienen suficiente energía específica para poderse usar en vehículos de autonomía media, o con vehículos híbridos. Aun no hay baterías que se puedan usar por sí solas para vehículos eléctricos con autonomías similares a los vehículos con motor de combustión interna (Larminie y Lowry, 2003). 104 Anexo 2. FASORES ESPACIALES En la teoría de circuitos de CA es común representar las cantidades sinusoidal variantes en el tiempo (voltajes y corrientes) por medio de fasores complejos. Con esto se tiene una forma simple de obtener soluciones para circuitos de CA. De forma similar, en máquinas eléctricas de CA, los voltajes, las corrientes y los enlaces de flujo, pueden representarse mediante fasores espaciales complejos, los cuales también son conocidos como vectores espaciales (Vas, 1993). En este reporte se usa el término fasor espacial en lugar de vector espacial. Un conjunto de variables trifásicas (ya sean voltajes, corrientes o enlaces de flujo) pueden expresarse mediante un fasor espacial, dicha representación consiste en número complejo cuya magnitud y ángulo pueden variar con el tiempo. Por ejemplo, una variable trifásica simétricas con devanados colocados a 2π/3 rad cada uno con respecto a los otros dos, con valores instantáneos fA(t), fB(t) y fC(t) de las fases a, b y c, respectivamente, se puede representar mediante el fasor espacial, 105 Anexo 2. Fasores espaciales 2 f = ⎡⎣1 f A ( t ) + a f B ( t ) + a 2 fC ( t ) ⎤⎦ = f e jα , 3 siendo: (A2.1) f el módulo o magnitud del fasor espacial, para variables trifásicas simétricas y balanceadas dicho módulo es igual a la amplitud máxima de los valores instantáneos fA(t), fB(t) y fC(t); α es el ángulo de fase y da la posición en la cual se j0 encuentra el valor máximo del fasor espacial f ; 1 = e , a = e j2 /3 2 ya =e j4π/3 son vectores unitarios en la dirección de los ejes magnéticos a, b y c, respectivamente. Para variables trifásicas fA(t), fB(t) y fC(t) simétricas y balanceadas, el lugar geométrico de f s es un circulo, donde la punta del fasor espacial gira en dirección positiva a una velocidad angular igual a la 2πf, donde f es la frecuencia en Hz de las variables trifásicas. En caso de variables trifásicas asimétricas el lugar geométrico del fasor espacial es una elipse o una línea recta. Para conocer el valor de f en una determinada posición proyectar el fasor espacial sobre el vector unitario e θ es necesario jθ . Para medir una posición alrededor del entrehierro de una máquina eléctrica de CA, la referencia es el eje real del MR estacionario (fijo al estator) y coincide con el eje magnético de la fase a del estator. Es importante señalar que el fasor espacial es únicamente una notación compleja que puede representar una variable trifásica y no necesariamente representa un vector físicamente. 106 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía Variables del estator Si se considera un devanado de estator trifásico simétrico, donde las fases individuales están desplazadas por un ángulo de 2π/3 rad cada una de las otras dos, como se muestra en la figura A2.1. Las tres fases del estator son sA, sB y sC, por simplicidad no se muestran en este diagrama los devanados del rotor. También se muestran los ejes magnéticos de las tres fases del estator, y los ejes real (sD) e imaginario (sQ) del MR fijo al estator. Figura A2.1. Diagrama esquemático de los devanados del estator. Una variable trifásica del estator, se puede representar entonces por el fasor espacial: 2 f s = ⎡⎣1 f sA ( t ) + a f sB ( t ) + a 2 f sC ( t ) ⎤⎦ = f s e jα s , 3 (A2.2) el cual tiene una nomenclatura similar a la de la ecuación (A2.1). Este fasor espacial 196H 197H se puede dividir en sus componentes sD y sQ, de la siguiente forma: f s = f sD + j f sQ . 107 (A2.3) Anexo 2. Fasores espaciales En la figura A2.2 se muestra el fasor espacial f s y sus componentes fsD y fsQ. La relación entre las componentes fsD y fsQ y las componentes trifásicas fsA, fsB y fsC, se expresa matricialmente como: ⎡1 ⎢ ⎡ f sD ⎤ ⎢f ⎥= 2⎢ 0 ⎢ sQ ⎥ 3 ⎢ ⎢1 ⎢⎣ f s 0 ⎥⎦ ⎢ 2 ⎣ −1 3 1 ⎤ 2 ⎥⎡ f ⎤ sA ⎥⎢ ⎥ 3 f − 2 ⎥ ⎢ sB ⎥ 1 ⎥ ⎢⎣ f sC ⎥⎦ 2 ⎥⎦ −1 2 2 2 (A2.4) donde la componente fs0 es igual a cero para variables trifásicas balanceadas. fs Figura A2.2. Fasor espacial de una variable trifásica del estator. Variables del rotor Para el rotor se consideran condiciones similares a las del estator mencionadas en la sección anterior, devanado trifásico simétrico y balanceado, donde las fases individuales están desplazadas por un ángulo de 2π/3 rad entre ellas. Las tres fases del rotor son ra, rb y rc. El MR fijo al rotor tiene dos componentes una real denotada por rα y una imaginaria denotada por rβ. 108 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía Una variable trifásica del rotor, se representa por el fasor espacial: 2 f r = ⎡⎣1 f ra ( t ) + a f rb ( t ) + a 2 f rc ( t ) ⎤⎦ = f r e jα r , 3 (A2.5) el cual tiene una nomenclatura similar a la de la ecuación (A2.1). Como se muestra 198H en la figura A2.3, este fasor espacial se puede dividir en sus componentes rα y rβ, de la siguiente forma: f r = f rα + j f r β . En la figura A2.3 también aparecen los ejes sD y sQ del estator. (A2.6) θr es el ángulo del rotor, el cual indica el desplazamiento angular entre el eje ra (o rα) del rotor y el eje sA (o sD) del estator. ωr es la velocidad a la cual gira el rotor. fr Figura A2.3. Fasor espacial de una variable trifásica del rotor. Al igual que para el estator, las componentes real e imaginaria y las componentes trifásicas, se relacionan mediante: ⎡1 ⎢ ⎡ f rα ⎤ 2 ⎢f ⎥= ⎢ 0 ⎢ rβ ⎥ 3 ⎢ ⎢1 ⎢⎣ f r 0 ⎥⎦ ⎢ 2 ⎣ −1 3 1 2 2 2 109 ⎤ 2 ⎥⎡ f ⎤ ra ⎥⎢ ⎥ 3 f − 2 ⎥ ⎢ rb ⎥ 1 ⎥ ⎢⎣ f rc ⎥⎦ 2 ⎥⎦ −1 (A2.7) Anexo 2. Fasores espaciales donde la componente fr0 es igual a cero para variables trifásicas balanceadas. Transformación entre marcos de referencia En ocasiones es necesario referir las variables del rotor al MR fijo al estator, o viceversa. También puede ser útil el utilizar algún MR distinto al del estator y rotor. En esta sección se aborda la transformación de las variables del estator y del rotor a un MR general, para posteriormente particularizar a los MR del estator y rotor. En la figura A2.4 se muestra un fasor espacial de una variable de estator f s en el MR del estator y su representación f sg en el MR general. El MR general gira a una velocidad ωg, y su posición respecto al eje sD es θg, su eje real se designa con la letra x y su eje imaginario con la letra y. La transformación del MR del estator al MR general se da mediante la siguiente expresión. f sg = f s e − jθ g = fs e ( j α s −θ g ) (A2.8) De (A2.8) se puede apreciar que el cambio de MR no afecta el módulo, en 20H cambio, el ángulo en el nuevo MR es igual a αs – θg. f s , f sg Figura A2.4. Fasor espacial del estator en el MR general. 110 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía El fasor espacial f s se puede dividir en sus componentes fsD y fsQ en el MR fijo al estator o en sus componentes fsx y fsy en el MR general. Las componentes de estos dos MR se relacionan mediante: ⎡ fsx ⎤ ⎡ cosθg senθg ⎤⎡ fsD ⎤ ⎢ f ⎥ = ⎢−senθ cosθ ⎥⎢ f ⎥ g g ⎦⎣ sQ ⎦ ⎣ sy ⎦ ⎣ En el caso particular cuando (A2.9) θg = θr, se tiene que el MR general se convierte en el MR fijo al rotor. Un fasor espacial del estator en el MR fijo al rotor se expresan mediante un apostrofe (´). Y las componentes de un fasor espacial del estator en el MR fijo al rotor se designan mediante sd y sq, como se muestra en la siguiente ecuación: f s ´= f s e− jθr = f s e j (α s −θ r ) (A2.10) f s ´= f sd + j f sq Un fasor espacial de una variable del rotor f r también se puede referir al MR general. En la figura A2.5 se representa este caso, cabe señalar que la posición θg del MR general se sigue midiendo a partir del eje sD del estator. La transformación del MR del rotor al MR general se da mediante la siguiente expresión. f rg = f r e ( − j θ g −θ r ) = fr e ( j α r −θ g +θ r ) (A2.11) Al igual que en el caso del fasor espacial del estator, el fasor espacial del rotor no cambia su módulo al cambiar al MR general, el único que cambia es su ángulo. 111 Anexo 2. Fasores espaciales f r , f rg Figura A2.5. Fasor espacial del rotor en el MR general. Para el fasor espacial del rotor, la relación entre sus componentes frα y frβ en el MR fijo al rotor y sus componentes frx y fry en el MR general es: ⎡ f rx ⎤ ⎡ cos (θ g − θ r ) sen (θ g − θ r ) ⎤ ⎡ f rα ⎤ ⎥⎢ ⎥ ⎢f ⎥=⎢ ⎢ ⎣ ry ⎦ ⎣ − sen (θ g − θ r ) cos (θ g − θ r ) ⎦⎥ ⎣ f r β ⎦ En el caso particular cuando (A2.12) θg = 0, se tiene que el MR general se convierte en el MR fijo al estator. Un fasor espacial del rotor en el MR fijo al estator se expresan mediante un apostrofe (´), y sus componentes se designan mediante rd y rq, como se muestra en la siguiente ecuación: f r ´= f r e jθr = f r e f r ´= f rd + j f rq 112 j (α r +θ r ) (A2.13) Anexo 3. CICLOS DE CONDUCCIÓN Existen dos tipos de pruebas que se pueden realizar con respecto al desempeño de un vehículo (eléctrico o de combustión interna). La primera, y más simple, es la prueba a velocidad constante, sin embargo, es una prueba poco realista debido a que un vehículo generalmente no trabaja a velocidad constante (Larminie y Lowry, 2003). La segunda prueba, más útil y compleja, es evaluar el desempeño del vehículo usando un perfil de velocidades cambiantes (ciclos de conducción). Existe un gran número de ciclos de conducción que se han desarrollado mediante la observación de los patrones de conducción típicos e intentan representar los perfiles de velocidad reales en diferentes condiciones. A continuación se presentan algunos ciclos de conducción reportados en la literatura (Larminie y Lowry, 2003), (Husain, 2003), (Emadi, 2005), (Ferreira et al, 2008), (Gao et al, 2007) los primeros tres son ciclos para zonas urbanas, desarrollados para medir las emisiones contaminantes de vehículos de combustión interna, y el último fue desarrollado específicamente para VE: • Federal Urban Driving Schedule (FUDS). La duración de este ciclo es de 1500 s y se muestra en la figura A3.1.a). 113 Anexo 3. Ciclos de Conducción • Simplified Federal Urban Driving Schedule (SFUDS). Es una versión simplificada del FUDS, el cual tiene una duración de únicamente 360 s, ver figura A3.1.b). Comparte algunas características con el FUDS como son: velocidad promedio, porción de tiempo estacionario (a velocidad cero), aceleración máxima y desaceleración máxima (frenado). • ECE-15. Es un ciclo de conducción de la comunidad europea para zonas urbanas, el cual es útil para probar el desempeño de vehículos pequeños, por ejemplo, un VE alimentado por baterías, ver figura A3.1.c). • SAE J227a. Es un estándar de la Asociación de Ingenieros Automotrices (SAE, por sus siglas en inglés “Society of Automotive Engineers”) el cual fue desarrollado específicamente para VE, figura A3.1.d). Consta de 4 versiones, cuyos parámetros se presentan en la tabla A3.1. Cada ciclo consta de varias fases: aceleración, velocidad constante, sin aplicar potencia (coast), frenado e inactividad (velocidad cero). Durante la fase donde no se aplica potencia, la velocidad no está especificada, pero la fuerza de tracción es cero, y el cambio de velocidad depende de la dinámica del VE. La versión más utilizada es la C, la cual es adecuada para VE pequeños para uso en zonas urbanas. Las versiones A y B se usan algunas veces para VE de propósito especial, por ejemplo, de reparto. 114 60 60 50 50 40 40 Velocidad (mph) Velocidad (mph) Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía 30 30 20 20 10 10 0 0 200 400 600 800 Tiempo (s) 1000 1200 0 1400 0 50 100 150 a) 200 Tiempo (s) 250 300 350 400 b) 55 50 45 Vmax 35 Velocidad (km/h) Velocidad (km/h) 40 30 25 20 Tvc Ta 15 10 Tf 5 0 Ti Tsp 0 20 40 60 80 100 120 Tiempo (s) 140 160 180 200 Tiempo (s) c) d) Figura A3.1. Ciclos de conducción: a) FUDS, b) SFUDS, c) ECE-15, d) SAE J227a. Tabla A3.1. Parámetros para las cuatro variaciones del SAE J227a. Parámetro Velocidad máxima, Vmax (km/h) Tiempo de aceleración, Ta (s) Tiempo de velocidad constante, Tvc (s) Tiempo sin potencia, Tsp (s) Tiempo de frenado, Tf (s) Tiempo de inactividad, Ti (s) Tiempo total, Tt (s) Ciclo A 16 4 0 2 3 30 39 115 Ciclo B 32 19 19 4 5 25 72 Ciclo C 48 18 20 8 9 25 80 Ciclo D 72 28 50 10 9 25 122 Anexo 4. PWM VECTORIAL La técnica de modulación llamada PWM vectorial o SVM (por sus siglas en inglés Space Vector Modulation) tiene mejor desempeño que otras técnicas de modulación, por ejemplo PWM senoidal (Holmes y Lipo, 2003). PWM vectorial es una alternativa para determinar los anchos de pulso de las señales de modulación para un inversor trifásico de dos niveles como el que se utiliza en este trabajo, cuyo diagrama se muestra en la figura A4.1. Figura A4.1. Inversor de dos niveles. 117 Anexo 4. PWM vectorial PWM vectorial se basa en el hecho de que en un inversor trifásico de dos niveles hay únicamente ocho combinaciones posibles de conmutación, cada una de estas genera un fasor espacial de voltaje. Así, este inversor puede proporcionar seis fasores espaciales de voltaje activos y dos fasores espaciales de voltaje cero. El fasor espacial de voltaje del inversor está dado por: ⎧2 ⎪ V exp ⎡⎣ j ( k − 1) π / 3 ⎤⎦ u k = ⎨ 3 cd ⎪⎩ 0 k = 1, 2,..., 6 (A4.1) k = 0, 7 donde Vcd es el voltaje del bus de CD. Como se puede observar de (A4.1), el módulo 201H de los seis fasores espaciales activos es igual, solamente cambia su ángulo. En el PWM vectorial, los seis fasores espaciales activos determinan seis sectores de π/3 rad, el primer sector se encuentra entre u1 y u2 , el segundo sector se encuentra entre u2 y u3 , y así sucesivamente. Un fasor espacial de voltaje us , de módulo máximo Vcd / 3 , puede ser formado por la suma de dos fasores espaciales contiguos y los dos fasores espaciales cero (Hassankhan y Khaburi, 2008). us = Tk T uk + k +1 uk +1 Ts Ts (A4.2) donde Ts = 1/fs es el periodo de conmutación a la frecuencia de conmutación fs, k es el sector en el cual se encuentra us , Tk es el tiempo durante el cual se aplica uk , Tk+1 es el tiempo durante el cual se aplica uk +1 . El tiempo restante para completar el 118 Control de la Operación de un Vehículo Eléctrico con un Uso Eficiente de la Energía periodo de conmutación T0 = Ts–Tk–Tk+1 se aplican los fasores espaciales u0 y u7 . Así, para los sectores impares, se tiene: 0 ≤ t < T0 / 4 ⎧ u0 ⎪u T0 / 4 ≤ t < T0 / 4 + Tk / 2 ⎪ k ⎪uk +1 T0 / 4 + Tk / 2 ≤ t < T0 / 4 + Tk / 2 + Tk +1 / 2 ⎪ us = ⎨ u7 T0 / 4 + Tk / 2 + Tk +1 / 2 ≤ t < 3T0 / 4 + Tk / 2 + Tk +1 / 2 ⎪u 3T0 / 4 + Tk / 2 + Tk +1 / 2 ≤ t < 3T0 / 4 + Tk / 2 + Tk +1 ⎪ k +1 3T0 / 4 + Tk / 2 + Tk +1 ≤ t < 3T0 / 4 + Tk + Tk +1 ⎪ uk ⎪u 3T0 / 4 + Tk + Tk +1 ≤ t < Ts ⎩ 0 (A4.3) y para sectores pares: 0 ≤ t < T0 / 4 ⎧ u0 ⎪u T0 / 4 ≤ t < T0 / 4 + Tk +1 / 2 ⎪ k +1 ⎪ uk T0 / 4 + Tk +1 / 2 ≤ t < T0 / 4 + Tk / 2 + Tk +1 / 2 ⎪ us = ⎨ u7 T0 / 4 + Tk / 2 + Tk +1 / 2 ≤ t < 3T0 / 4 + Tk / 2 + Tk +1 / 2 ⎪u 3T0 / 4 + Tk / 2 + Tk +1 / 2 ≤ t < 3T0 / 4 + Tk + Tk +1 / 2 ⎪ k 3T0 / 4 + Tk + Tk +1 / 2 ≤ t < 3T0 / 4 + Tk + Tk +1 ⎪uk +1 ⎪u 3T0 / 4 + Tk + Tk +1 ≤ t < Ts ⎩ 0 (A4.4) Para calcular los tiempos Tk y Tk+1 se utilizan las siguientes fórmulas: Tk = 3 ( us Ts sin π − α s 3 Vcd u Tk +1 = 3 s Ts sin (α s ) Vcd siendo αs el ángulo de us respecto a uk . 119 ) (A4.5) Anexo 4. PWM vectorial Para ejemplificar el principio de la técnica de PWM vectorial, en la figura A4.2, se presenta el caso donde el fasor espacial de voltaje us se encuentra en el sector 1, es decir, k = 1. Por tanto se puede formar por la suma de u1 , u2 , u0 y u7 : us = T1 T u1 + 2 u2 Ts Ts (A4.6) sQ u3 = (010) u2 = (110) T2 u2 Ts u4 = (011) us u1 = (100) s sD T1 u1 Ts u7 = (111) u0 = (000) u5 = (001) u6 = (101) Figura A4.2. Principio del PWM vectorial. Las señales de modulación Sa, Sb y Sc para este caso se muestran en la figura A4.3, tal como lo establece la ecuación (A4.3) la secuencia de los fasores espaciales 20H es u0 , u1 , u2 , u7 , u2 , u1 y u0 , por ser un sector impar. u0 u1 u2 u7 u2 u1 Figura A4.3. Señales del PWM vectorial. 120 u0