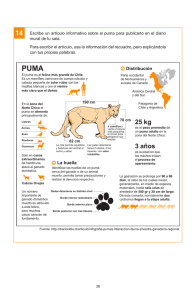
Texto completo

P ROYECTO I NTEGRADOR DE LA
C ARRERA DE I NGENIERÍA N UCLEAR
Modelado del núcleo de la Central Nuclear
Atucha 2 con el código neutrónico de cinética 3D
PARCS: casos estacionarios y transitorios
Joaquín Rubén Basualdo Perelló
Ing. Aníbal Blanco
Director
San Carlos de Bariloche
Junio 2007
Instituto Balseiro
Universidad Nacional de Cuyo
Comisión Nacional de Energía Atómica
Argentina
A mis padres
y a mi gran familia.
Resumen
Este trabajo está enmarcado en el desarrollo de un simulador para una Central Nuclear Argentina. Una representación precisa del comportamiento físico
del reactor —con las herramientas disponibles actualmente— implica acoplar
un código neutrónico de cálculo de núcleo de cinética 3D con un código termohidráulico de planta. Enfocados en el carácter neutrónico de esta tarea, estudiamos un código de cinética espacial 3D. El profesor Tom Downar, de la
escuela de ingeniería nuclear de la Universidad de Purdue, nos facilitó el código de cinética 3D PARCS. Este código, que es usado por la USNRC (United
States Nuclear Regulatory Commission), está extensamente validado en el cálculo
de transitorios acoplado con los códigos termohidráulicos de planta RELAP5
y TRACE en centrales del tipo PWR y VVER.
Utilizando PARCS modelamos y analizamos estados estacionarios y transitorios del núcleo de la Central Nuclear Atucha 2. En los casos posibles, comparamos los resultados obtenidos con resultados disponibles de PUMA (código
de núcleo de la línea de cálculo oficial de Atucha 2). Estudiamos los conceptos
básicos del cálculo de reactores y los conceptos fundamentales del cálculo de
núcleo —enfocados en el código PARCS— necesarios para luego enfrentar el
problema del acople con un código termohidráulico de planta.
Palabras clave: SIMULACIÓN DE TRANSITORIOS DE NÚCLEO, PARCS,
CÁLCULO NEUTRÓNICO, CÁLCULO DE NÚCLEO, ATUCHA 2, CINÉTICA
3D
Abstract
This work is carried out under the frame of the development of an Argentinean Nuclear Power Plant Simulator. To obtain the best representation of the
reactor physical behavior —utilizing the state of the art tools— this Simulator
should couple a 3D neutronics core calculation code with a thermo-hydraulics
system code. Focused in the neutronic nature of this job, we studied a 3D kinetics code. Dr. Tom Downar, professor of the Nuclear Engineering School of
the Purdue University, facilitated us the 3D reactor core simulator PARCS. This
code, which is used by the USNRC (United State Nuclear Regulatory Commission), is widely validated in transient calculations coupled with the thermohydraulics system codes RELAP5 and TRACE.
Utilizing PARCS, we modeled and performed steady-state and transients
calculations of the Nuclear Power Plant Atucha 2 core. Whenever is possible,
we compare our results against the results obtained with PUMA (the official
core code for Atucha 2) . We study the fundamental concepts on reactor core codes —focused in PARCS— necessaries to later face the problem of the
coupling with a thermo-hydraulics system code.
Keywords: NEUTRONIC/THERMOHYDRAULIC COUPLING, ATUCHA 2,
CORE CALCULATION, NEUTRONICS CALCULATION, 3D NEUTRON KINETICS, PARCS, CORE TRANSIENT SIMULATION
Contenidos
1. Introducción
1.1. Nociones generales sobre cálculo neutrónico de un reactor
1.1.1. Distintos niveles en el cálculo neutrónico . . . . . .
1.2. Estado estacionario, cinética y dinámica . . . . . . . . . . .
1.3. Códigos neutrónicos/termo-hidráulicos acoplados . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
1
2
2
4
5
2. El código de núcleo PARCS
2.1. Los problemas a resolver . . . . . . . . . . . . . . . .
2.1.1. El problema del reactor crítico asociado en k
2.1.2. El problema transitorio con fuente fija . . . .
2.2. El método CMFD . . . . . . . . . . . . . . . . . . . .
2.3. Los métodos nodales ANM, NEM y TPEN . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
9
9
10
10
11
12
3. Modelado del núcleo de Atucha 2
3.1. Modelado en geometría cartesiana . .
3.1.1. El modelo de la celda . . . . . .
3.2. Modelado en geometría hexagonal . .
3.3. Las secciones eficaces . . . . . . . . . .
3.3.1. La tarjeta XSEC . . . . . . . . .
3.3.2. El módulo GenPMAX . . . . .
3.4. Modelado de las barras de control . .
3.4.1. Las barras de control en PUMA
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
13
14
15
16
16
17
17
18
18
.
.
.
.
.
.
.
.
.
20
20
25
26
28
32
35
36
40
42
4. Resultados y Comparaciones
4.1. Núcleo fresco . . . . . . . . . . . . .
4.1.1. Aplicación del método NEM
4.1.2. Cálculos con ADF . . . . . . .
4.1.3. Comparaciones con PUMA .
4.2. Cálculos con Boro . . . . . . . . . . .
4.2.1. Búsqueda de Boro . . . . . .
4.3. Cálculos de quemado . . . . . . . . .
4.3.1. Núcleo de equilibrio . . . . .
4.4. Núcleo con barras de control . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
4.4.1. Todas las barras insertadas . . . . . . . . . . . . .
4.4.2. Núcleo fresco con tubos guías . . . . . . . . . . . .
4.4.3. Comparación con PUMA de las 4 primeras barras
4.5. Geometría hexagonal . . . . . . . . . . . . . . . . . . . . .
4.5.1. Núcleo fresco . . . . . . . . . . . . . . . . . . . . .
4.5.2. Núcleo con tubos guía . . . . . . . . . . . . . . . .
4.6. Análisis de transitorios . . . . . . . . . . . . . . . . . . . .
4.6.1. SCRAM . . . . . . . . . . . . . . . . . . . . . . . .
4.6.2. Eyección de BC . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
42
45
47
51
51
53
55
55
59
5. Conclusiones
61
A. Evaluación del Proyecto
A.1. Organización del trabajo . . . . . . . . . . . . . . . . . . . . . . .
A.2. Análisis Económico . . . . . . . . . . . . . . . . . . . . . . . . . .
63
63
63
B. Documentación del código PARCS
B.1. Núcleo fresco con corrección de ADF en geometría cartesiana
B.2. SCRAM en núcleo fresco con geometría hexagonal . . . . . . .
B.2.1. Archivo barras_hex.bar . . . . . . . . . . . . . . . . . .
B.3. Ejemplo de un archivo PMAX . . . . . . . . . . . . . . . . . . .
66
66
69
70
71
.
.
.
.
Referencias
73
vi
C APÍTULO I
Introducción
Este trabajo está enmarcado en el desarrollo de un simulador para una Central Nuclear Argentina. Una representación precisa del comportamiento físico
del reactor —con las herramientas disponibles actualmente— implica acoplar
un código neutrónico de cálculo de núcleo de cinética 3D con un código termohidráulico de planta. Enfocados en el carácter neutrónico de esta tarea, estudiamos el código de cinética espacial 3D PARCS (Purdue Advanced Reactor
Core Simulator) como una posible opción para la implementación en el simulador. Este código, que es usado por la USNRC (United States Nuclear Regulatory
Commission), está extensamente validado en el cálculo de transitorios acoplado
con los códigos termohidráulicos de planta RELAP5 y TRACE en centrales del
tipo PWR y VVER. La versión 2.71 del código nos fue cedida para uso académico por su autor, el Dr. Tom Downar, de la escuela de ingeniería nuclear de la
Universidad de Purdue. PARCS es utilizado actualmente por la ARN (Autoridad Regulatoria Nuclear Argentina) para el modelado de transitorios (secuencias accidentales) en el reactor Atucha 2, por este motivo, algunos desarrollos
fueron hechos en PARCS —dadas las características únicas que presentan las
barras de control de este reactor— que permiten modelar el mismo.
Con el objetivo de estudiar la aplicabilidad el código PARCS a Atucha 2,
desarrollamos un modelo del núcleo del mismo, éste se realizó de manera tal
que los resultados pudieran ser contrastados de manera directa con resultados del código PUMA utilizado por NA-SA (Nucleoeléctrica Argentina S.A.).
La escasez de información de secciones eficaces para distintos estados del núcleo no nos permite lograr un modelo con realimentación termohidráulica1 , sin
embargo, se estudian las características principales del código.
Empezamos estudiando los fundamentos básicos del cálculo de reactores.
Luego, usando como ejemplo el código PARCS, analizamos cómo funciona un
código de cálculo de núcleo y aplicamos lo aprendido en el modelado del núcleo del reactor Atucha 2. Finalmente analizamos los resultados y las comparaciones realizadas contra PUMA.
1
No estamos hablando aquí de realizar un acople con un código termohidráulico de planta
sino sólo de utilizar el modelo termohidráulico bidimensional interno del código.
1.1.
Nociones generales sobre cálculo neutrónico de
un reactor
Cualquier cálculo o modelado de un reactor nuclear empieza con las especificaciones ingenieriles y una biblioteca de datos neutrónicos (ENDF, NJOY, etc.)
y termina con la distribución de potencia del núcleo. La física de reactores trata
de determinar la distribución de neutrones en espacio, energía y tiempo. Esta
determinación podrá hacerse en forma analítica siempre que la simplicidad del
problema lo permita, de otra manera, será determinada numéricamente (como
sucede en realidad).
La distribución espacial, energética y temporal de los neutrones se establece
por la interacción de los mismos con los materiales del sistema en consideración. Las propiedades de este sistema están descritas completamente por las
secciones eficaces para neutrones y el comportamiento de los neutrones está
gobernado por la ecuación de transporte. Si consideramos variaciones temporales de la distribución neutrónica suficientemente rápidas, debemos tener en
cuenta los neutrones retardados, cuyo comportamiento está descrito por las
correspondientes constantes de decaimiento λi y las fracciones βi .Las ecuaciones que resuelven el problema neutrónico serán introducidas en el siguiente
capítulo. Para entender y predecir el comportamiento de un reactor, tenemos
que conocer los ritmos de reacción involucrados, la distribución de potencia,
el factor de multiplicación y los coeficientes de reactividad. Por esto, el cálculo
de un reactor es una herramienta esencial en el diseño y análisis del mismo.
1.1.1.
Distintos niveles en el cálculo neutrónico
En general, el cálculo neutrónico se realiza en distintas etapas o niveles. Empieza enfocado en el elemento representativo más pequeño, es decir, la barra
combustible, siguiendo con el elemento combustible completo y finalmente todo el núcleo. Mientras que el tamaño del sistema considerado se incrementa, se
pasa de una representación detallada a una más tosca de las variables energía y
espacio. En cada paso el flujo obtenido se usa para producir por condensación
y homogeneización las secciones eficaces para los pasos subsiguientes. Este
enfoque es válido puesto que en un cálculo de celda2 , uno está interesado en
fuertes variaciones locales entre regiones de distintos materiales. En el cálculo
del elemento combustible observamos la interacción entre las barras y en un
cálculo de núcleo observamos la interacción entre los elementos combustibles.
2
En la jerga se llama cálculo de celda al cálculo realizado al nivel de barra o elemento
combustible donde se aplica una descripción detallada de las variables energía y espacio y se
calcula mediante métodos de transporte.

A nivel de la barra combustible3 , el flujo varía fuertemente en la región
térmica debido a la fuerte absorción del metal pesado. Por esta razón en este
nivel es necesario usar la mejor aproximación práctica de la ecuación de transporte. En general, en este nivel se usan métodos de probabilidad de colisión y
la cantidad de grupos de energía es del orden de la centena. Para estos cálculos debemos conocer las secciones eficaces de los materiales que componen
las distintas regiones, en general, se calcula con celdas cilíndricas equivalentesy condiciones de contorno reflexivas para simular un arreglo infinito. En la
realidad no existe un arreglo de celdas que sea estrictamente regular debido a
que existen distintas heterogeneidades como pueden ser, gaps de agua, barras
de control, venenos quemables o distintos enriquecimientos.
En el cálculo a nivel de elemento combustible se utilizan en general métodos de transporte, por ejemplo, Ordenadas Discretas o SN , con 6-10 grupos
de energía. Las secciones eficaces son constantes en las discretizaciones espaciales. De esta manera, se deben condensar las bibliotecas a 6-10 grupos de
energía y se debe describir cada barra o pin equivalente como homogéneo.
Vaina
Combustible
Refrigerante
Canal
Moderador
Moderador / Reflector
Gap
Barra Combustible
Elemento Combustible
Núcleo
Figura 1.1: Representación de distintos niveles de cálculo neutrónico.
En la Fig. 1.1 observamos un esquema de los distintos niveles del cálculo
neutrónico. El primer paso es calcular en el nivel más interno con una muy
buena representación energética y espacial, de aquí obtenemos secciones eficaces a menos grupos y homogeneizadas espacialmente para realizar los cálculos
en el próximos nivel. En el segundo nivel se calcula el elemento combustible,
aquí la pastilla, el gap de gas y la vaina están representados por un nuevo material resultado de la homogeneización anterior. De la misma manera, en el
último nivel los elementos combustibles son representados por una única sec3
Podría ser también una placa en un elemento combustible tipo MTR u otro tipo de geome-
tría.

ción eficaz resultado de las condensaciones y homogeneizaciones anteriores.
La condensación (que se refiere a energía) se calcula como
X
Σx,G =
Σx,g · φg
g∈G
X
φg
g∈G
donde Σ representa una sección eficaz macroscópica, φ el flujo neutrónico y los
subíndices x y g la reacción en cuestión y los grupos de energía contenidos en
el grupo G respectivamente. Mientras que para la homogeneización debemos
tener en cuenta tanto flujos como volúmenes:
X
Σx,I =
Σx,i · φi · Vi
i∈I
X
φi · Vi
i∈I
aquí V es el volumen y el subíndice i representa la i-ésima región contenida en
I.
Los cálculos de núcleo describen la interacción entre los elementos combustibles. Dado el tamaño del reactor, los cálculos se realizan en 1-3 grupos de
energía. La lenta variación del flujo a lo largo del reactor permite el uso de la
ecuación de difusión. La solución numérica se lleva a cabo a través de un mallado grueso, a menudo cada nodo de esta malla (en el plano axial) representa
un elemento combustible más el gap de agua. Por esto las secciones eficaces se
condensan a nivel del conjunto completo (elemento combustible + gap de agua
+ canal, etc.), estos juegos de secciones eficaces se ordenan en tablas y cada
elemento combustible típico posee su propia tabla. En éstas se agregan variaciones (secciones eficaces incrementales) tales como concentración de boro,
densidad del refrigerante, temperatura del combustible, etc. con las que luego
se realizarán interpolaciones para calcular las secciones eficaces de un estado
particular. El próximo paso en el cálculo de reactores consiste en el cálculo de
todo el núcleo por métodos de transporte. En la actualidad existen códigos que
realizan este tipo de cálculos pero carecen de uso práctico debido al elevado
costo computacional.
1.2.
Estado estacionario, cinética y dinámica
Un código neutrónico puede realizar cálculos estacionarios o dependientes del
tiempo. Aunque en el análisis del estado estacionario la derivada temporal en

la ecuación de transporte es nula, estos cálculos se aplican en varios fenómenos temporales. Un ejemplo es el caso del cálculo de quemado del núcleo que
se describe como una secuencia de estados estacionarios combinada con la solución temporal de los isótopos relevantes.
En un cálculo temporal nos interesa evaluar el comportamiento del reactor
ante una determinada perturbación. La nomenclatura cinética y dinámica es en
cierta forma desafortunada dado que ambas representan fenómenos temporales. En general, la mayoría de los textos diferencian a éstas en que en la cinética no se considera la realimentación de variables y en la dinámica sí. Mientras que la cinética predice respuestas temporales de la población de neutrones
ante cambios de la reactividad, la dinámica de reactores describe cómo estos
cambios de reactividad son producto de perturbaciones externas, tomando en
cuenta realimentaciones por temperatura, coeficientes de vacío, etc. Así, la dinámica involucra el análisis de la interacción de la mayoría de los sistemas del
circuito primario y por lo tanto está involucrada en los análisis de seguridad.
Los códigos neutrónicos llamados de cinética 3D, poseen en general la capacidad de realizar estos cálculos dinámicos, tal es el caso del código PARCS.
Sin embargo, para un análisis completo de la física que ocurre durante un transitorio, el código neutrónico debe estar acoplado a un código termohidráulico.
En el capítulo siguiente estudiaremos esto más detalladamente.
1.3.
Códigos neutrónicos/termo-hidráulicos acoplados
Los reactores nucleares que operan hoy en día fueron calculados utilizando
discretizaciones poco detalladas. Ante la imposibilidad de realizar cálculos con
mayor fidelidad se adoptaron criterios conservativos. La suma de estos criterios
conservativos dieron como resultado reactores sobredimensionados en cuanto
a seguridad y por lo tanto más costosos y menos económicamente competitivos.
La capacidad actual de los procesadores permite cálculos tridimensionales
donde se tienen en cuenta al mismo tiempo todas las variables físicas involucradas en la dinámica del reactor. Así podemos diseñar reactores menos costosos sin comprometer el nivel de seguridad y además echar luz sobre los procesos físicos que se desarrollan durante un transitorio. Es decir, estos cálculos
nos permiten mejorar seguridad, economía, diseño y conocimiento. Esta situación fue advertida por la OECD/NEA (Organization for Economic Co-operation
and Development/ Nuclear Energy Agency) que inició un proyecto [7, 8] que tiene como finalidad organizar y aprovechar la actual capacidad para realizar
cálculos más realistas del comportamiento de un reactor nuclear. Actualmente

en el mundo existe una nueva tendencia en el cálculo de reactores que consiste
en realizar cálculos acoplados neutrónicos/termo-hidráulicos 3D. De la misma
manera, los organismos reguladores en materia de reactores nucleares se están
volcando a aceptar estos cálculos, cambiando así de un criterio conservativo a
lo que se conoce como criterio de la mejor estimación.
La necesidad de códigos acoplados es mayor en cálculos en donde hay una
fuerte realimentación entre la neutrónica y el refrigerante así como también
en las situaciones en donde la excursión de potencia es importante y su distribución cambia durante el transitorio. Los RIA (Reactivity Initiated Accidents) constituyen uno de los más importantes y menos resueltos problemas
en cuestiones de seguridad nuclear. La ventaja de usar códigos acoplados 3DNC/THSC (3D-neutronic code/thermohidraulic system code) se hace evidente en el análisis de transitorios con una fuerte asimetría en los cuales el modelo
simple de cinética puntual o un modelo unidimensional no son capaces de proveer una solución aceptable desde el punto de vista del comportamiento físico
del fenómeno.
Existen dos formas de acoplar los códigos 3D-NC/THSC, la primera es en
serie o de manera integrada, en la que se deben realizar modificaciones mayores en ambos códigos. Una importante desventaja de este método es que
implica importantes modificaciones en ambos códigos. La segunda es en paralelo, en la que ambos códigos se ejecutan paralelamente intercambiando información a través de algún sistema como PVM (parallel virtual machine), MPI
(message passage interfase) o método similar.
1.3.0.1.
Códigos Termo-hidráulicos de planta
Estos códigos están basados en general, en la resolución simultanea de seis
ecuaciones de balance de masa, momento y energía para cada fase, líquido y
vapor. Resuelven una geometría unidimensional, aunque existen técnicas de
nodalización que permiten simular una geometría tridimensional ficticia. Las
incertezas mayores de estos códigos provienen de las relaciones constitutivas,
empíricas o semiempíricas que determinan la evolución de las dos fases. Las
soluciones numéricas aproximadas son otra fuente de incertezas aunque no
constituyen el problema principal.
Para modelar el aspecto térmico del núcleo poseen un módulo de cinética
puntual o a lo sumo un enfoque de cinética unidimensional4 . Es común también modelarlo con una función temporal (resultado de una medición o de
algún cálculo con un código neutrónico). Consecuentemente no se puede simular una distribución de potencia tridimensional y en algunos casos se usa
4
Esto no se aplica para el caso del código RELAP-3D que tiene incorporado el código de
cálculo neutrónico tridimensional NESTLE.

un factor de potencia de núcleo estático. Algunos códigos termohidráulicos
reconocidos que existen en la actualidad son:
ATHLET (Analysis of T-H of Leaks and Transients) para LWR.
RELAP 5 (USNRC vesion)
RELAP 3D (DOE version) este código tiene la capacidad de aplicar 3D
T-H en zonas selectas y está acoplado con el código neutrónico 3D NESTLE.
CATHARE-2 (CEA)
TRAC-PF1 (Los Alamos National Laboratory), TRAC-PF1/MOD2 (Purdue State University), TRAC-M (USNRC), TRAC-BF1 (para BWR).
POLCA-T
1.3.0.2.
Códigos Neutrónicos
Los códigos neutrónicos no tienen el problema de error en las ecuaciones sino
en las aproximaciones utilizadas para resolverlas como por ejemplo, la conocida ecuación de difusión. Existen soluciones como las obtenidas con el método
de Monte Carlo que son inclusos tomadas como benchmarks para contrastar el
resto de las soluciones. Como consecuencia los métodos numéricos de resolución juegan un rol importante en las incertezas, mucho más que en los códigos
termo-hidráulicos. Para calcular las realimentaciones de reactividad por variación de densidad del refrigerante, el coeficiente de vacío, etc. estos códigos
poseen en general un pequeño módulo termo-hidráulico que se limita al RPV
y cálculos sencillod de trasferencia de energía. Algunos códigos de cinética 3D
reconocidos internacionalmente son:
DYN3D.
NESTLE (North-Carolina State University).
PARCS (Purdue State Univesity).
QUABOX
1.3.0.3.
El acople neutrónico-termohidráulico
Existen efectos físicos que no pueden ser modelados por estos códigos funcionando independientemente uno del otro, por ejemplo, supongamos un MSLB
(Main Steam Line Break) en un PWR que genera un desbalance local de potencia. Esto no puede modelarse por ninguno de los dos códigos por separado,
sin embargo, sí puede ser modelado si trabajan acoplados.

Entrada
Termohidráulica
cl
Entrada
neutrónica
Interfase
Termohidráulica
sf
Tc
Tc
Tc
ρv
ρl
α
Tm
P
B
Termohidráulica
Mapa
T/H
Q
(A) ⇔ (AB)
Estructura
de memoria
(A)
Interfase
neutrónica
Interfase
Mapa
Neut.
cl′
sf ′
Tc′ Tc Tc
ρv′ ρl′ α′
Tm′ P′ B′
Neutrónica
Q′
(AB) ⇔ (B)
Estructura
de memoria
(AB)
Estructura
de memoria
(B)
Figura 1.2: Esquema de acople neutrónico termohidráulico.
La tendencia mundial es el realizar cálculos con el enfoque del best estimate,
teniendo por lo tanto que modelar los fenómenos físicos con tanta exactitud
como se pueda. La Fig. 1.2 muestra un esquema de cómo se acoplan los códigos. Dado que ambos utilizan diferentes mallados, es necesario transformar los
resultados al formato correspondiente. Este esquema corresponde, por ejemplo, al uso de PVM. El programa termohidráulico hace una corrida, actualiza
los valores del programa neutrónico y éste genera una nueva distribución de
potencias que será devuelta al programa termohidráulico. En contraparte, el
código neutrónico recibe la actualización de un gran número de variables que
influyen en el cálculo neutrónico, como ser, densidad del moderador (ρ), temperatura del moderador (Tm ), temperatura del combustible (Tc ), coeficiente de
vacío (α), etc.

C APÍTULO II
El código de núcleo PARCS
PARCS es un código de cálculo de núcleo que resuelve problemas de estado
estacionario y dependientes del tiempo en un espacio tridimensional. PARCS
resuelve las ecuaciones multigrupo de difusión o SP31 en geometría cartesiana,
cilíndrica o hexagonal. Existe una versión acoplado directamente al código de
cálculo termohidráulico de planta TRACE para cálculo de transitorios y puede
acoplarse al código RELAP-5 a través del uso de PVM (Parallel Virtual Machine).
El módulo GENPMAX se usa para procesar las secciones eficaces generadas
por los códigos de celda y llevarlas al formato PMAX utilizado por PARCS.
2.1.
Los problemas a resolver
La solución de problemas de cinética espacial debe tratar problemas físicos
como el transporte de neutrones y la generación y decaimiento de precursores.
Se deben resolver el problema del reactor crítico asociado en k y la ecuación de
transporte con dependencia temporal.
El primer paso para resolver estos problemas es discretizar en espacio y en
el caso de dependencia temporal también en tiempo. Para la discretización en
tiempo PARCS utiliza métodos alfa2 , además de una integración analítica de
segundo orden en los precursores. En caso de prever un comportamiento exponencial se aplica una transformada exponencial. La discretización temporal
permite pasos de tiempo grandes aún en transitorios que involucren inserciones de reactividad super-prompt critical. Para la discretización espacial PARCS
utiliza un nodalizado en el que se resuelve el método CMFD (Coarse Mesh Finite
Difference) y el método de dos nodos para encontrar los coeficientes de corrección para las corrientes internodales.
1
2
Es el método PN truncado para N = 3 con algunas simplificaciones [1].
Que para α = 0,5 nos devuelve el bien conocido método de Crank-Nicholson.
2.1.1.
El problema del reactor crítico asociado en k
PARCS resuelve básicamente dos tipos de problemas neutrónicos, el problema
del autovalor del reactor crítico asociado en k, es decir kef f y el problema de la
fuente fija. Para resolver el estado estacionario previo a un cálculo de transitorio, se resuelve el problema del reactor crítico asociado en k. Supongamos una
geometría cartesiana discretizada una forma nodal. Para un nodo m las ecuaciones de balance que rigen el comportamiento temporal del flujo neutrónico
son:
1 dφm
g
νgm dt
=
1
G
X
χpg
kef f
X
−
g=1
u=x,y,z
dCkm
dt
=
G
1 X
kef f
K
X
m
νpg Σm
f g φg + χdg
λk Ckm +
k=1
G
X
m
Σg 0 g φm
g0
(2.1)
g=1
1
m+
m−
m
Jgu
− Jgu
− Σm
tg φg
m
hu
m
m
νdgk Σm
f g φ g − λ k Ck
(2.2)
g=1
la simbología es la típica utilizada en cualquier libro de texto, siendo φm
g el
flujo medio en el nodo m en el grupo de energía g, Ckm la densidad media de
precursores del grupo k, etc. Para cálculos de estado estacionario, las derivadas temporales son nulas y no se hace distinción entre neutrones prompt y
retardados. El sistema a resolver es entonces
M φ = λF φ ≡
1
kef f
Fφ
donde M es la llamada matriz de migración y F la matriz de producciones.
Para resolver este sistema se resuelve
φn+1 = λF φ ≡
1
n
kef
f
F φn
utilizando el método de Wielandt [11] para acelerar la convergencia.
2.1.2.
El problema transitorio con fuente fija
Para resolver la Ec. 2.1 varias aproximaciones se utilizan en la ecuación a dos
grupos de energía. Se tienen en cuenta las siguientes simplificaciones:
χp1 = χd1 = 1, χp2 = χd2 = 0 (espectro de fisión en el grupo rápido)
los neutrones retardados no dependen de la energía de los neutrones.
m
m
νdgk Σm
f g = βk νΣf g = (1 − β)νΣf g

Σm
21 = 0 (no up-scattering)
Así el problema a resolver en cada nodo es:
1 dφg
vg dt
=




(1 − β) ·
1
2
X
kef f
νΣf g φg +
g=1
K
X
λk Ck − L1 − Σr1 φ1 , g = 1
k=1


 Σs12 φ1 − L2 − Σr2 φ2
dCk
dt
= βk ·
1
2
X
kef f
,g = 2
νΣf g φg − λk Ck
g=1
siendo L1 y L2 términos que representan las fugas. Aplicando una discretización temporal con el método α y una integración analítica de segundo orden
de la ecuación de precursores y empleando una discretización espacial que involucra los métodos CMFD (Coarse Mesh Finite Difference) y dos nodos se plantea
un problema transitorio con fuente fija. Además, aprovechando el conocimiento de una evolución temporal con características exponenciales, se realiza una
transformación exponencial en el flujo [1]. De esta manera (con una adecuada elección del período) el flujo transformado variará más lentamente con el
tiempo dado que la componente rápida de la variación es absorbida por la
parte exponencial de la transformada, logrando así poder trabajar con pasos
de tiempo más grandes.
2.2.
El método CMFD
La ecuación de balance para cada nodo esta acoplada con la del nodo vecino,
a través de los términos de fuga. Este acoplamiento se resuelve usando un
método nodal en el que la corriente en la interface entre cualesquiera dos nodos
adyacentes se calcula como
m±
m±
m±
u
u
Jgu
= ∓D̃gu
φm±l
− φm
− D̂gu
φm±l
− φm
g
g
g
g
(2.3)
donde m ± lu representa el índice del nodo vecino (en la Fig. 2.1 vemos un
m±
m±
esquema de este acoplamiento), D̃gu
es un coeficiente de acoplamiento y D̂gu
es un factor de corrección. El factor de corrección es calculado mediante los
métodos de dos nodos ANM (Analytic Nodal Method), NEM (Nodal Expansion
Method) [13] o una combinación de ambos. Para el caso de geometría hexagonal
se usa el método TPEN (Triangle-based Polinomial Expansion Nodal) [12].
Luego de insertar la Ec. 2.3 en la Ec. 2.1, de aplicar los métodos de discretización temporal y espacialmente e integrar la ecuación de los precursores analíticamente bajo algunas suposiciones, obtenemos un sistema lineal de

Figura 2.1: Discretización axial de las barras de control.
ecuaciones conocido como problema de transitorio de fuente fija con CMFD3 .
Este problema se resuelve con un método iterativo. PARCS utiliza el método
BiCGSTAB (Bi-Conjugated Gradient Stabilized) , precondicionado con BILU3D
(Blockwise Incomplete LU Factorization) para resolver este problema (capítulo 3
de referencia [1]).
2.3.
Los métodos nodales ANM, NEM y TPEN
Los métodos nodales, tienen como finalidad conseguir un buena exactitud en
el cálculo usando un mallado relativamente grande (de aquí el nombre de coarm±
se mesh). Para lograr esto ajustan un coeficiente de corrección (D̂gu
Ec. 2.3) de
manera aumentar la exactitud del resultado.
Los métodos ANM, NEM y TPEN tienen la finalidad de encontrar el coeficiente de corrección que se usa para calcular las corrientes en cada interfase.
Por esto, este problema se resuelve en cada interfaz del dominio. El método
NEM es más robusto que el ANM, que tiene problemas de convergencia cuando k ≈ 1. El método TPEN se usa para geometría hexagonal. En definitiva
el método CMFD con los métodos nodales consisten en resolver diferencias
finitas en un mallado grueso, aplicando un coeficiente de corrección que corrigen el acoplamiento entre los nodos. Este coeficiente de corrección se calcula
una vez cada varias iteraciones del método de diferencias finitas logrando así
un cálculo mas exacto con un menor costo computacional. Esta estrategia de
cálculo se conoce como estrategia de iteración no lineal.
3
El desarrollo completo se encuentra en la referencia [1].

C APÍTULO III
Modelado del núcleo de
Atucha 2
Para explicar el modelado del núcleo de Atucha 2 veamos primero cómo es su
geometría.
Figura 3.1: Esquema del núcleo de CNA2.
En la Fig. 3.1 observamos claramente que el núcleo tiene geometría hexagonal.
Este núcleo posee 451 elementos combustibles de uranio natural con 18 barras
de control que se insertan en forma inclinada y están distribuidas en 6 bancos
de 3 barras cada uno. En estos bancos cada barra se encuentra a 120◦ respecto
de la otra para lograr una distribución simétrica. La inclinación de las barras
varía entre los 17 y los 25◦ . La mitad de las barras son grises y la mitad negras.
Además estas barras están tienen distintas composiciones en sus partes superior e inferior con el objetivo de obtener una mejor distribución de potencia.
Las barras negras tiene un núcleo de hafnio desnudo en la parte inferior y recubierto por acero en la parte superior. Las barras grises son completamente de
acero y en la parte superior es más gruesa que la parte inferior.
3.1.
Modelado en geometría cartesiana
Dada la geometría del núcleo, lo lógico es hacer un modelo hexagonal. Sin
embargo, a fines de hacer comparaciones con los resultados obtenidos con el
código PUMA modelamos primeramente utilizando geometría cartesiana. En
PARCS cada nodo representa —de alguna manera— un canal combustible. A
fines prácticos, un nodo tiene las mismas propiedades que cualquier otro y en
un cálculo son indistinguibles, pero existen ciertas propiedades que se pueden
asignar al modelo que hacen que un nodo se comporte como si fuera un elemento combustible. Este es el caso, por ejemplo, del factor de corrección ADF
(Assembly Discontinuity Factor). Este factor se aplica a cada cara de un nodo y
es una relación entre el flujo en la cara y el flujo medio del nodo que se obtiene del cálculo de celda, más adelante volveremos sobre esto y se verá más
claramente.
Figura 3.2: Esquema del núcleo de CNA2 en geometría cartesiana.

En la Fig. 3.2 vemos el núcleo en geometría cartesiana. En esta figura se
pueden observar claramente los 451 elementos combustibles. PARCS usa una
representación cartesiana, que es un arreglo rectangular. Esta geometría no se
puede representar directamente sino que hay que dividir los canales1 , al menos
en 4 rectángulos nodos. En la Fig. 3.3 podemos observar el tipo de división
utilizada.
4
5
3
1
6
2
7
Figura 3.3: División de los canales utilizada en el modelado.
En cuanto a la discretización axial dividimos la longitud activa (530cm) en
20 planos para ser coherentes con el modelo de PUMA y tomamos 4 planos
para el reflector superior y 4 para el reflector inferior.
3.1.1.
El modelo de la celda
Dado que la geometría del núcleo de Atucha 2 es hexagonal, la celda típica será
hexagonal.En la Fig. 3.4 mostramos como se la equivalencia entre la geometría
hexagonal y la cartesiana de una celda.
Figura 3.4: Esquema del pasaje de una celda hexagonal a una cartesiana.
1
Cuando hablamos de canales nos referimos a cada rectángulo de la Fig. 3.2 que representa
un elemento combustible.

3.2.
Modelado en geometría hexagonal
El modelado del núcleo en geometría hexagonal es bastante directo ya que
cada nodo representa un elemento combustible (Fig. 3.5). La mayor desventaja
de esta geometría es el modelado de las barras de control, dado que existen
situaciones en las que la posición de un nodo de la barra de control puede no
corresponder muy bien a la realidad como veremos cuando presentemos los
resultados del modelo en geometría hexagonal. Este problema es menor en la
geometría cartesiana debido a que los nodos son más pequeños.
Figura 3.5: Esquema del núcleo de CNA2 en geometría hexagonal.
Una ventaja importante de la geometría hexagonal es la velocidad del cálculo. Esto es lógico debido a que utiliza la cuarta parte de los nodos que la geometría cartesiana.
3.3.
Las secciones eficaces
Para el modelado del núcleo disponemos de los juegos se secciones eficaces
utilizados en las entradas de los cálculos realizados con PUMA. El formato de
secciones eficaces de PUMA para cálculos a 2 grupos de energía es: D1 , D2 , Σa1 ,

Σs12 , Σs21 , Σa2 , νΣf 1 , νΣf 1 , κΣf 1 , κΣf 2 . Aquí κΣf es la sección eficaz de fisión
multiplicado por la energía liberada en la fisión medida en MeV. En realidad
el verdadero formato de PUMA no utiliza κΣf 1 sino simplemente la sección
eficaz de fisión y por otro lado da la energía de fisión. Pero en general se iguala
esta energía de fisión a 1 y usa como dato de entrada κΣf 1 , en vez de Σf 1 .
PARCS es un código que está ordenado en forma modular. Uno de estos
módulos es el encargado de manejar las tablas de secciones eficaces. En realidad, PARCS posee dos de estos módulos y el uso de uno anula el uso del otro.
Estos dos módulos poseen distintas estructuras de secciones eficaces que son la
estructura XSEC y la estructura PMAX.
3.3.1.
La tarjeta XSEC
El input de PARCS se divide en tarjetas que agrupan conjuntos de datos, existe
así, una tarjeta donde se define la geometría, una donde de especifica el tipo de cálculo, una donde se especifican las propiedades de los materiales y
varias más. La tarjeta XSEC es una de las formas que posee PARCS para ingresar las secciones eficaces. En esta tarjeta se ingresan además otros parámetros
que corresponden a características de los materiales que componen los nodos
y a los nodos mismos, como ser el antes mencionado ADF o el CDF (Corner
Discontinuity Factor). En esta tarjeta la estructura para las secciones eficaces es
Σtr1 , Σa1 , νΣf 1 , κΣf 1 , Σs12 , Σtr2 , Σa2 , νΣf 2 , κΣf 2 , Σf 1 , Σf 2 2 . Vemos que los datos
utilizados por PUMA son casi los mismos que utiliza PARCS excepto por Σtr
utilizado por PARCS. Para solucionar esto utilizamos la aproximación
Σtr =
1
3·D
esto es válido, dado que para obtener los coeficientes de difusión para PUMA
a partir de la salida del código de celda se utilizó la relación inversa.
3.3.2.
El módulo GenPMAX
Como lo mencionamos anteriormente, el módulo GenPMAX [14] se encarga
de tratar las salidas de los códigos de celda3 para llevarlos al formato PMAX
que puede ser interpretado por PARCS. GenPMAX genera archivos que luego
serán archivos de entradas (inputs) de PARCS. El uso de este módulo anula casi
completamente la tarjeta XSEC. La ventaja de utilizar el formato de secciones
eficaces PMAX, es que la interpolación de secciones eficaces es cuadrática en
2
3
Estas dos últimas son opcionales y deben estar si se hacen cálculos con xenón y samario.
Es compatible con los códigos HELIOS, TRITON y CASMO.

vez de lineal como con la tarjeta XSEC. Recordemos que PARCS hace la suposición Σs21 = 0 para resolver por difusión. Para mejorar esta aproximación se
corrige Σs12 como sigue:
Σs12P ARCS = Σs12cc −
φ2 · Σs21cc
φ1
donde cc se usa para código de celda y φ son los flujos obtenidos con el código
de celda.
La estructura de secciones eficaces utilizada en el formato PMAX es: Σtr1 ,
Σtr2 , Σa1 , Σa2 , νΣf 1 , νΣf 2 , κΣf 1 , κΣf 2 , Σs11 , Σs21 , Σs12 , Σs22 . Aquí Σs12 es siempre
cero por lo que vimos en el capítulo anterior. Observemos que esta estructura
de secciones eficaces requiere además las secciones eficaces de in-scattering
que PUMA no requiere. Ante la transformar las secciones eficaces del formato
PUMA al formato PARCS se adoptó Σs11 = Σs22 = 0. Esto no representa ningún
inconveniente dado que las secciones eficaces de in-scattering no intervienen
en la sección eficaz de remoción.
3.4.
Modelado de las barras de control
El modelado de las barras de control de Atucha 2 es un punto fundamental
debido a la particularidad de estas barras de entrar de manera inclinada. En
PARCS se implementó una forma para modelar estas barras exclusivamente
para el cálculo de Atucha 2. Este modelado consiste en discretizar la barra
en trozos como muestra la Fig. 3.6 y definir en la entrada del programa las
coordenadas de cada uno de los trozos que componen la barra.
Se pueden definir varios tipos de composiciones en su longitud lo que es
útil debido a que las barras de Atucha 2 están compuestas de manera distinta
en su parte superior e inferior. La declaración de una barra de control presupone un tubo guía que la rodea. De esta manera la mismas coordenadas se usan
para el tubo guía, pero sólo un juego de secciones eficaces incrementales define
al tubo guía.
3.4.1.
Las barras de control en PUMA
PUMA utiliza el mismo modelo de barras que PARCS, es decir discretiza la
barra transversalmente. De esta manera, una comparación en geometría cartesiana entre PUMA y PARCS debería ser directa. El único detalle a tener en
cuenta al momento de trasformar las secciones eficaces incrementales del formato PUMA al formato PMAX son las secciones eficaces de la parte superior.
Denotaremos como Σsup a las secciones eficaces incrementales correspondientes al material de la parte superior y como Σinf a las correspondientes a la

Figura 3.6: Discretización axial de las barras de control.
parte inferior. Para definir una barra con distintas composiciones PUMA define en realidad dos barras distintas. Una barra va desde la parte superior del
núcleo a la parte inferior y tiene como secciones eficaces incrementales Σinf y
la otra barra va desde la parte superior hasta la longitud correspondiente al
cambio de material y tiene como secciones eficaces incrementales Σsup − Σinf .
Esta es la única consideración extra que se debe tener en cuenta en la migración
de las secciones eficaces del formato PUMA al formato PMAX.

C APÍTULO IV
Resultados y Comparaciones
En este capítulo se muestran los resultados obtenidos en el modelo del núcleo
de Atucha 2 usando el código PARCS y se comparan estos resultados contra
cálculos con PUMA. Dado que nuestro objetivo es entender cómo funciona
y aprender a usar PARCS, aplicamos las distintas características del mismo y
probamos los distintos métodos de cálculo, correcciones y aproximaciones. En
los primeros casos la geometría utilizada es la cartesiana, más adelante estudiamos los resultados obtenidos con la geometría hexagonal. Las comparaciones
realizadas contra PUMA son válidas dentro de ciertos límites, dado que –en
algunos casos– las tablas de secciones eficaces utilizadas presentan discrepancias con las que deberían haberse utilizado, de todas manera, para lograr el fin
deseado estas comparaciones son suficientes.
4.1.
Núcleo fresco
El caso más sencillo de modelar es el de estado estacionario para núcleo fresco.
Las características de este modelo son:
Núcleo homogéneo.
No se consideran barras de control.
No se consideran tubos guía.
Secciones eficaces sin quemado.
No se consideran venenos (Xe, Sm).
Podemos pensar este caso como una gran masa homogénea formada por
óxido de uranio mezclado con canales y agua, rodeado por otra gran masa de
agua (reflector). Las secciones eficaces y longitudes utilizadas corresponden
a las de núcleo fresco con combustible y moderador calientes generadas por
NA-SA , que nos las cedió para realizar este estudio.
El caso que se presenta a continuación se hizo transformando directamente
las secciones eficaces del formato PUMA al formato PMAX (ver sección 3.3), el
método de cálculo utilizado es Diferencias Finitas (de ahora en adelante FDM).
Los cálculos realizados de aquí en más tienen condición de contorno de corriente entrante nula, a menos que se explicite lo contrario. En todos los casos
se usó el formato PMAX para dar entrada a las secciones eficaces.
Figura 4.1: Distribución de potencia del núcleo fresco calculada con Diferencia Finitas.
En el gráfico 4.1 observamos la distribución de potencia obtenida en el núcleo. La distribución está normalizada con la potencia media. Dado que no
estamos considerando por separado los venenos Xe ni Sm, esta distribución
es independiente del nivel de potencia. Como dijimos anteriormente PARCS
fuerza Σs21 = 0, pero se puede realizar una corrección en Σs12 de manera de
tener en cuenta el up-scattering. A continuación analizaremos la corrección que
se debería aplicar a Σs12 .
Pensemos en un reactor infinito, es decir no consideraremos las fugas, además, por simplicidad en la notación consideremos un reactor homogéneo y
supondremos un estado estacionario. Las ecuaciones para dos grupos de energía suponiendo que los neutrones se generan rápidos son
ν1
ν2
· Σf 1 φ1 +
· Σf 2 φ2 + Σs21 φ2 − Σs12 φ1 − Σa1 φ1
k∞
k∞
0 = Σs12 φ1 − Σs21 φ2 − Σa2 φ2
0 =

en estas ecuaciones la notación usada es la típica, los subíndices 1 y 2 representan el flujo rápido y térmico respectivamente. Esto también se puede escribir
como
Σs21 φ2
ν
ν
· Σf 2 φ2 = Σa1 φ1 + Σs12 −
φ1 −
· Σf 1 φ1
k∞
φ1
k∞
Σs21 φ2
Σa2 φ2 =
Σs12 −
φ1
φ1
haciendo
Σ∗s12
obtenemos
Σs21 φ2
=
Σs12 −
φ1
ν
ν
· Σf 2 φ2 = Σa1 φ1 + Σ∗s12 φ1 −
· Σf 1 φ1
k∞
k∞
Σa2 φ2 = Σ∗s12 φ1
(4.1)
(4.2)
(4.3)
Pensemos que esta misma deducción es válida para un estado no estacionario y un reactor finito. De esta manera, si la relación φ2 /φ1 es constante en el
reactor y ésta es la misma en el cálculo con el código de celda y en el cálculo
con el código de núcleo, entonces la aproximación es exacta. Estudiemos entonces la forma de los flujos rápido y térmico (Fig. 4.2) en nuestros cálculos. En
la Fig. 4.3 observamos el cociente de los flujos rápido y térmico (φ1 /φ2 ).
Figura 4.2: Distribución de flujo rápido (a la izquierda) y térmico (a la derecha).
Si bien esta distribución de flujos térmico y rápido corresponde al plano
axial n◦ 19, ésta es similar en todos los planos axiales del núcleo. El cociente

Figura 4.3: Cociente entre flujos rápido y térmico (φ1 /φ2 ).
(φ2 /φ1 ) es prácticamente constante en el interior del núcleo mientras que no lo
es en los bordes, por esto, la aproximación utilizada es menos buena aquí. Sin
embargo debemos tener en cuenta que en los bordes la condensación y homogeneización de las secciones eficaces tampoco es muy buena debido a que en
el cálculo de celda tampoco se tiene en cuenta la interfase del combustible con
el reflector.
Para entender el impacto de realizar esta corrección, estudiamos cómo varía
kef f ante una variación en Σs12 . La Fig. 4.4 muestra la dependencia de kef f
cuando variamos Σs12 sólo en el combustible y cuando variamos Σs12 en todos
los materiales (combustible y reflectores). Podemos observar que la variación
de kef f está regida por la variación de Σs12 en el combustible. En este caso, Σs21
es del orden de la cincuentava parte de Σs12 , basados en la Fig. 4.3 la corrección
(ecuación 4.1) es del orden del 1-5 %, lo que corresponde a un ∆kef f ≈ 1-4mk.
Ésta es una variación considerable y por este motivo estudiamos que sucede al
aplicarla. Para esto usamos la relación φ2 /φ1 = 1,94 que obtenemos en el caso
sin corrección tomando un promedio de los cocientes de los flujos integrados
axialmente. Un análisis más detallado implica una iteración con el cociente
φ2 /φ1 obtenido luego de aplicar la corrección, pero la variación de este cociente
es muy pequeña y la primera iteración es suficiente.
La variación en la distribución de potencia se puede observar en la Fig. 4.5.
Ésta variación es muy pequeña, sin embargo, si comparamos los kef f de ambos

cálculos, la diferencia es considerable. Para el cálculo sin la corrección, kef f =
1,08457 y con la corrección aplicada kef f = 1,08121. En este punto conviene
hacer una comparación entre los resultados obtenidos con PARCS y con PUMA
en los distintos casos.
CÓDIGO
Forma de cálculo
PUMA
forzando Σs21 = 0
PARCS
sin corrección en Σs12
PUMA
usando Σs21 normalmente
PARCS
aplicando la corrección a Σs12
kef f
1.08474
método FDM 1.08457
método NEM 1.08470
1.08126
método FDM 1.08107
método NEM 1.08121
Tabla 4.1: Comparación entre los resultados obtenidos con PARCS y PUMA.
1.10
∆XS combustible
∆XS todo
1.08
1.06
keff
1.04
1.02
1.00
0.98
-50
-40
-30
-20
-10
0
% variacion Σs12
Figura 4.4: kef f en función de variaciones en Σs12 .
Anticipándonos a las resultados posteriores, podemos ver el buen acuerdo que tienen los cálculos realizados con ambos códigos. Dado que el código
PUMA trabaja con la ecuación de difusión a dos grupos sin hacer la simplifi-

Figura 4.5: Variación porcentual de la potencia calculada con corrección respecto de la calculada sin
corrección en Σs12 .
cación Σs21 = 0, concluimos que ésta aproximación es muy buena en la predicción del kef f obteniendo diferencias menores que 0,2 mk. Este resultado es el
que esperamos debido a que la condición φ2 /φ1 = cte es válida prácticamente en todo el núcleo. Las mayores discrepancias se encuentran en los bordes
(Fig. 4.5) tal como lo esperamos.
4.1.1.
Aplicación del método NEM
PARCS fue pensado primeramente para cálculo de reactores PWR, por este
motivo tiene implementado métodos de cálculos nodales como mencionamos
en el capítulo 2. Estos métodos buscan aumentar el orden de la solución sin
consumir mayores recursos computacionales. A continuación realizamos el
mismo cálculo anterior, usando el método nodal NEM1 . De aquí en adelante no se aplicará la corrección en Σs12 . En la Fig. 4.6 observamos la diferencia
entre las distribuciones de potencia obtenidas con los distintos métodos de
cálculos. Observamos que la distribución de potencia calculada con el método
nodal tiene menos curvatura. En cuanto a kef f , obtenemos kef fN EM = 1,08470 y
kef fF DM = 1,08457.
1
Nodal Expansion Method, ver capítulo 2.

Figura 4.6: Variación porcentual de la potencia calculada con el método NEM respecto de la calculada
con FDM.
El método de cálculo nodal permite agregar correcciones a los modelos.
Una de estas correcciones tiene que ver con la discontinuidad entre los elementos combustibles. El factor ADF (Assembly Discontinuity Factor) se obtiene
del cálculo de celda y es una relación entre el flujo medio y el flujo en el borde
de la celda. En PUMA se usa un factor de discontinuidad que tiene como finalidad corregir el flujo en la interfaz con el reflector [4]. La relación entre entre
el factor de discontinuidad que usa PUMA y el ADF es del tipo inversa2 .
4.1.2.
Cálculos con ADF
Como mencionamos en el capítulo 3, PARCS trata cada nodo como si fuese un
elemento combustible (EC) a fines de definir sus propiedades. Por ejemplo, el
ADF es un factor de discontinuidad que se debe definir en cada cara del EC.
Debido a que cada nodo tiene un identificador que usa para asignarle sus propiedades, resulta cómodo tratar al nodo como un EC. En nuestro caso, cada EC
está dividido en 4 nodos de manera que la asignación directa de los factores de
corrección no es posible. Por este motivo, debemos representar al núcleo homogéneo cómo si estuviese compuesto de 4 materiales distintos, en la Fig. 4.7
2
En los manuales de PARCS [1] y [2] no hay una definición detallada del ADF, sin embargo,
de acuerdo a el autor del código PARCS, ésta es la relación que debe usarse.

se ejemplifica esto. Cada color representa un EC y cada EC está formado por
4 composiciones. Estas composiciones son idénticas, a excepción del factor de
discontinuidad ADF. La composición 1 tendrá los valores de discontinuidad
para las caras norte y oeste, mientras que no se aplicará corrección en las caras
este y sur. De la misma manera la composición 2 tendrá correcciones en las caras norte y este, pero no en las caras este y sur. Calculamos entonces aplicando
la corrección por ADF.
N
1
2
1
2
O
3
4
3
4
1
2
1
2
1
2
3
4
3
4
3
4
1
2
1
2
3
4
3
4
1
2
3
4
E
S
Figura 4.7: Esquema de composición del núcleo.
Figura 4.8: Variación porcentual de la potencia calculada con ADF respecto de la calculada sin ADF.

r=
φconADF − φsinADF
φsinADF
(4.4)
Recordemos que sólo podemos aplicar la corrección cuando usamos el método NEM. Los kef f obtenidos son: kef fN EM = 1,08470 y kef fADF = 1,08436. La
variación en la distribución de potencia al aplicar el factor de discontinuidad,
resulta en una distribución más curvada, anticipándonos a resultados posteriores, ésta es aún más curvada que la distribución calculada con FDM, cumpliendo así el objetivo de bajar la potencia en los bordes.
4.1.3.
Comparaciones con PUMA
A continuación mostramos las comparaciones entre los resultados obtenidos
con PARCS contra PUMA. PUMA es un código de difusión con Diferencias
Finitas [6], que se usa en la línea oficial de cálculo para las centrales Embalse y
Atucha 1 y 2. Existen numeros estudios de validación de PUMA contra MCNP
y que muestran un ajuste, en general, menor que el 3 % (referencias [5, 15]). Al
contrastar los resultados de PARCS con los de PUMA pretendemos, de alguna manera, validar los cálculos realizados con PARCS. En general, las línea de
cálculo que usa PARCS tiene a HELIOS como código de celda. La línea usada
por PUMA (en este caso) tiene a WIMS y DRAGON como códigos de celda.
Como dijimos anteriormente, no disponemos de las salidas de WIMS y DRAGON sino de las entradas para PUMA. Dado que no podemos corregir Σs12
por no poseer los flujos de los cálculos de celda y aún cuando vimos que la
corrección es buena si usamos los flujos del cálculo de núcleo, decidimos forzar Σs12 = 0 en los cálculos de PUMA, de esta manera, las ecuaciones resueltas
por PUMA son las mismas que las resueltas por PARCS3 . Como dijimos, PUMA tiene la posibilidad de aplicar una corrección que mejora los resultados
obtenidos, por cuestiones que veremos a continuación decidimos aplicar esta
corrección. Los cálculos con PUMA fueron realizados por un experto.
En la Tabla 4.2 comparamos los kef f obtenidos en cada caso. Vemos que el
ajuste en kef f es muy bueno en todos los casos. Podemos observar cómo el kef f
tiene una relación directa con la forma de la distribución de potencia, mientras menos curvada es la distribución, mayor es el kef f . En el límite, para una
distribución plana, obtendríamos k∞ .
En la Fig. 4.12 observamos la variación en la distribución de potencia en
los cálculos de PUMA sin y con corrección, elkef f correspondiente a el cálculo
sin la corrección es kef f = 1,08509. Podemos rescatar dos cosas, primero, que
la variación en la distribución de potencias con y sin corrección es similar a
3
En estos casos Difusión a dos grupos.

kef f
PUMA
1.08474
PARCS-NEM 1.08470
PARCS-FDM 1.08457
PARCS-ADF 1.08436
Tabla 4.2: Comparación de los kef f obtenidos en los distintos cálculos
la variación que se obtiene en PARCS utilizando el método NEM con y sin
ADF, y segundo, que en ambos casos (PUMA y PARCS con y sin corrección) la
variación ∆kef f ≈ -0.4 mk.
Figura 4.9: Variación porcentual de la potencia calculada con PUMA respecto de la calculada con FDM
con PARCS.

Figura 4.10: Variación porcentual de la potencia calculada con PUMA respecto de la calculada con
NEM con PARCS.
Figura 4.11: Variación porcentual de la potencia calculada con PUMA respecto de la calculada con
ADF con PARCS.

Figura 4.12: Variación porcentual de la potencia calculada con PUMA sin y con corrección.

4.2.
Cálculos con Boro
En esta sección realizamos nuevamente cálculos con Diferencias Finitas y el
método NEM con y sin la corrección de ADF, esta vez para la condición de
núcleo frío con 16ppm de boro. El propósito es mostrar al menos un caso más
de cálculo para estado estacionario y luego introducir un nuevo concepto, el
de las secciones eficaces incrementales.
Figura 4.13: Distribución de potencia.
La Fig. 4.13 muestra la distribución de potencia en el núcleo, esta es similar
a la observada anteriormente para el núcleo fresco. En las Figs. 4.14, 4.15 y 4.16,
mostramos las comparaciones de los resultados obtenidos con PARCS contra
el caso de PUMA sin corrección de discontinuidad. Recordemos que en PUMA
la corrección de discontinuidad disminuye la potencia en los bordes, es decir,
esperamos aún menores diferencias. En todos los casos la potencia calculada
con PARCS en los bordes es menor que la calculada con PUMA. Recordemos
que no estamos aplicando la corrección en Σs12 , sin embargo, la variación de
potencia debido a esta corrección es mínima como mostramos en la sección
anterior (Fig. 4.5) y no afecta las comparaciones aquí realizadas, por otra parte
en los cálculos de PUMA estamos forzando Σs21 = 0. Este será el último caso
donde no consideramos la corrección de discontinuidad en PUMA dado que
nos interesa comparar con los resultados con la corrección aplicadas que es
como fueron contrastados contra MCNP.

kef f
PUMA sin corrección 1.00249
PARCS-NEM
1.00225
PARCS-FDM
1.00217
PARCS-ADF
1.00206
Tabla 4.3: Comparación entre los kef f obtenidos en los distintos cálculos.
En la Tabla 4.3 se comparan los resultados obtenidos para los kef f , observamos el mismo comportamiento que en caso anterior con núcleo fresco. Nuevamente la diferencias son menores que 0.5 mk en todos los casos.
Figura 4.14: Variación porcentual de la potencia calculada con PUMA respecto de la calculada con
FDM con PARCS.

Figura 4.15: Variación porcentual de la potencia calculada con PUMA respecto de la calculada con
NEM con PARCS.
Figura 4.16: Variación porcentual de la potencia calculada con PUMA respecto de la calculada con
ADF con PARCS.

4.2.1.
Búsqueda de Boro
Como vimos, la reactividad en exceso del núcleo fresco es muy alta, en el caso
de Atucha 2 βef f ≈ 720 lo que significan ≈ 10 $ de reactividad en exceso. Anticipándonos a resultados posteriores, esta reactividad es mayor que la
reactividad negativa introducida por las barras de control. Por este motivo en
el arranque del núcleo y también en las puestas en marcha que se hagan antes
que el núcleo haya alcanzado un estado de quemado determinado, es necesario envenenar el núcleo con boro. PARCS puede calcular la concentración de
boro necesaria para obtener un estado de criticidad. Para esto usa secciones eficaces incrementales. Debemos entonces dar a PARCS un conjunto de secciones
eficaces incrementales correspondientes a distintas concentraciones de boro.
Dado que solo poseemos las secciones eficaces incrementales para 0 y 16ppm
damos un único punto con el que PARCS realizará las interpolaciones. Debido
a que la concentración necesaria para lograr la criticidad es mayor que 16ppm
damos la opción de extrapolar. Para 16,5ppm obtenemos kef f = 1,00003, no
mostramos una distribución de potencia pues es redundante. Si bien este caso
no es particularmente útil, introduce el uso de las secciones eficaces incrementales. Este es el mismo tratamiento que se da en los casos cuando se calcula una
nueva condición de temperatura o un nuevo coeficiente de vacío en el caso de
un cálculo acoplado a un código termohidráulico. Estas secciones eficaces incrementales si bien son parecidas a las de las barras de control, no se tratan
de la misma manera. En el capítulo 7 de la referencia [1] hay una descripción
detallada del tratamiento de las secciones eficaces incrementales.

4.3.
Cálculos de quemado
Una característica fundamental de los cálculos de núcleo, necesaria para las estrategias de recambio, es el cálculo de quemado. Estos cálculos, si bien se tratan
de una evolución temporal, se calculan de manera estática. Es decir, el programa calcula un estado estacionario y con este resultado (distribución espacial de
potencia) y el paso de quemado calcula cual es el quemado correspondiente a
cada nodo del núcleo de la siguiente manera:
∆Bi = ∆Bc
Pi · Gc
Pc · Gi
(4.5)
donde ∆B es el quemado en el correspondiente paso temporal, P la potencia, G la cantidad de metal pesado y los subíndices i y c representan la i-ésima
región y el núcleo completo respectivamente. Es decir que para calcular el quemado debemos conocer, además de las secciones eficaces, la cantidad de uranio
que hay en cada zona. En cada paso del quemado, para cada nodo, se calcula el
juego de secciones eficaces correspondientes. Luego se calcula la distribución
de potencias para este nuevo estado y se realiza un nuevo paso de quemado.
Este proceso es válido siempre que el tiempo entre dos puntos de quemado
sea tal que la distribución de potencia en el núcleo varíe poco. Típicamente se
usan pasos de algunos días.
Acabamos de introducir un nuevo concepto, que corresponde al cálculo de
las secciones eficaces dependiendo del quemado. Para lograr esto, se debe proveer a PARCS con tablas de secciones eficaces con distintos puntos de quemado. Una vez que PARCS calcula el quemado de un nodo, busca en las tablas de
secciones eficaces e interpola el valor correspondiente a este quemado. PARCS
usa interpolación de segundo orden si se utiliza el módulo PMAX y lineal si se
utiliza la tarjeta XSEC, existe también la posibilidad de extrapolación. Como
dijimos en un principio, usamos el módulo PMAX.
La Fig. 4.17 muestra la evolución de kef f en el tiempo. Durante la evolución
el núcleo permaneció siempre a plena potencia. En el gráfico observamos una
abrupta caída de kef f que se debe a la acumulación de Xe y Sm. Observamos
luego un crecimiento de kef f ocasionado por la aparición de Pu239 y finalmente
kef f cae monótonamente.
En la Fig. 4.18 observamos la distribución del quemado del núcleo a los 100
días. Como esperamos el quemado tiene cierta semejanza con la distribución
de potencia. En la Fig. 4.19 vemos la distribución de potencia del núcleo a
los 100 días. Debido a que el quemado es mayor del centro hacia afuera, la
distribución de potencia es mucho más plana comparada con la del núcleo
fresco. Finalmente, en la Fig. 4.20 observamos la diferencia relativa entre los

1.085
PUMA
FDM
NEM
1.080
1.075
1.070
1.065
keff
1.060
1.055
1.050
1.045
1.040
1.035
1.030
1.025
0
20
40
60
80
100
Días
Figura 4.17: Comparación entre cálculos de variación de kef f con el quemado.
Figura 4.18: Distribución del quemado a los 100 días.

Figura 4.19: Distribución del potencia a los 100 días.
quemados calculados con PUMA y PARCS (con el método NEM). Vemos que
efectivamente el núcleo está más quemado en el cálculo con PUMA donde
la potencia es mayor (ver Fig. 4.10). En la Fig. 4.21 observamos la diferencia
en la distribución de potencias entre los resultados obtenidos con PUMA y
los obtenidos con el método NEM de PARCS. Si volvemos a ver la Fig. 4.10,
veremos que estos resultados son muy similares, la única diferencia es que
ahora las discrepancias en los bordes se acentúan. Donde el flujo es mayor en
PUMA habrá entonces un mayor quemado respecto del calculado con PARCS,
pero esto debería, entonces, disminuir las diferencias. La explicación de que la
diferencia en vez de disminuir aumente se encuentra en que, en estas zonas,
el quemado es menor que el del pico por plutonio (ver Fig.s 4.18 y 4.17), por
lo que, mientras no se pase el quemado correspondiente a este pico, un mayor
quemado corresponde a una mayor reactividad.

Figura 4.20: Comparación entre el quemado calculado con PUMA y el calculado con PARCS a los 100
días.
Figura 4.21: Comparación entre la distribución de potencia con PUMA y NEM a los 100 días.

4.3.1.
Núcleo de equilibrio
El núcleo de equilibrio es fundamental para establecer un modelo de núcleo
que se usará como base para los cálculos de análisis de transitorios y otros estudios del núcleo. Para un cálculo de núcleo en equilibrio, es necesario tener
un mapa del quemado del núcleo, esto es, el quemado correspondiente a cada nodo. Este quemado fue calculado, siguiendo una estrategia planeada de
antemano. En PARCS el mapa de quemado se debe dar en un archivo externo
donde se especifica el quemado de cada uno de los nodos, en este caso, de los
37040 nodos.
Figura 4.22: Distribución de potencia para el núcleo de equilibrio.
En la Fig. 4.22 observamos la distribución de potencias para una distribución de quemado dada. En la Fig. 4.23 observamos la diferencia entre los cálculos realizados con PUMA y PARCS, vemos que los resultados ajustan muy
bien. En cuanto a kef f , para PUMA kef f = 1,01293 y para PARCS kef fN EM = 1,01360.

Figura 4.23: Comparación entre distribución de potencias obtenidas con PUMA y PARCS.

4.4.
Núcleo con barras de control
Para completar el modelo del núcleo modelamos las barras de control. El caso
de las barras de control de Atucha 2 es un caso muy particular, debido a que
como se explicó en el capitulo anterior, están inclinadas. El problema radica
en que los códigos comerciales modelan únicamente barras verticales u horizontales. El código PARCS fue modificado recientemente para poder modelar
estas barras inclinadas. En la entrada del código se debe describir la geometría de cada barra nodo a nodo. Una vez definida la geometría de la barra, se
pueden asignar distintas composiciones para cada sección de la misma. Esto
es muy útil en el caso de Atucha 2 debido a que las barras tienen la peculiaridad de estar compuestas de manera distinta en su parte superior e inferior.
Las propiedades de la barra de control se definen a través de secciones eficaces
incrementales y de la misma manera para los tubos guía. Para el cálculo de las
secciones eficaces incrementales se deben calcular tres celdas. La celda sólo con
los combustibles, la celda con combustibles y el tubo guía y finalmente la celda con combustibles, tubo guía y barra de control. Luego, las secciones eficaces
incrementales se obtienen haciendo la diferencia con los resultados obtenidos.
Así, las secciones eficaces incrementales para el tubo guía corresponden a la
diferencia del cálculo con combustible y tubo guía, menos el cálculo solo con
combustible. Análogamente para las secciones eficaces incrementales de las
barras de control.
4.4.1.
Todas las barras insertadas
Como primer resultado con las barras de control insertadas presentamos el
caso de núcleo fresco con todas las barras de control insertadas. Los cálculos
son realizados usando el método NEM.
Para este caso kef f = 1,01526, como anticipamos la reactividad negativa introducida por todas las barras no es suficiente para compensar la reactividad
en exceso del núcleo fresco, por lo que para el arranque se deberá usar boro.
En las Figs. 4.24 y 4.25 observamos la distribución de potencia distintos planos.
Recordemos que el plano 24 es el superior y el plano 5 el inferior. La potencia
es menor en los planos superiores que en los inferiores debido a que las barras
son más absorbentes en la parte superior. Vemos cómo en los planos centrales
la potencia es mayor. En cada plano podemos ver las depresiones de potencia
debido a la presencia de las barras, de esta manera se puede también seguir
cada barra y verificar que su modelado es correcto, trabajo que se realizó satisfactoriamente.

Figura 4.24: Distribución de potencia en los planos axiales 24 al 15.

Figura 4.25: Distribución de potencia en los planos axiales 14 al 5.

4.4.2.
Núcleo fresco con tubos guías
Este modelo corresponde al núcleo fresco, sin barras de control y con el modelo
de tubos guías. El modelado de los tubos guías es inmediato una vez que se
modelaron las barras de control, dado que en el cálculo afectan a los mismos
nodos que éstas.
Figura 4.26: Distribución de potencia para el caso de todas las barras extraídas.
Observamos en la Fig. 4.26 la distribución de potencia para el caso de todas
las barras insertadas, para este caso kef f = 1,04602. A continuación realizamos
una comparación con los resultados obtenidos con PUMA.
En la Fig. 4.27 vemos que la diferencia en la distribución de potencia es muy
grande, aún más, para PUMA kef f = 1,08297 si lo comparamos con el valor
obtenido con PARCS vemos que la diferencia es enorme (36,95 mk). Aquí debemos detenernos un momento para analizar este resultado. Éste es el primer
resultado que comparamos donde estamos usando las secciones eficaces incrementales. Basándonos en la información que tenemos y que describimos en
el capítulo 3, las secciones eficaces incrementales fueron migradas del formato PUMA al formato PARCS de manera satisfactoria. Se controló la geometría
de las barras una por una, se controlaron las secciones eficaces de referencia y
las secciones eficaces incrementales. Además, se consultó a expertos en PARCS
acerca del formato utilizado para las secciones eficaces incrementales y del input del programa para el modelo de las barras. En cada caso, no se encontró

Figura 4.27: Diferencia entre PARCS y PUMA para el caso solo con tubos guías.
ningún error. Por otro lado, los resultados de PUMA fueron validados contra cálculos de MCNP [5, 4, 15] por lo que debemos aceptarlos como correctos
con ajustes menores del 3 %. En esta situación concluimos que los resultados
obtenidos con nuestro modelo con PARCS no son satisfactorios. Sin embargo,
dado que nuestro interés se centra en aprender a utilizar el código, decidimos
seguir adelante con los cálculos, teniendo en cuenta que se debe solucionar
este problema.

4.4.3.
Comparación con PUMA de las 4 primeras barras
Con el objeto de contrastar algunos resultados más, decidimos modelar y comparar la inserción de las barras 1 a 4. En este modelo no se encuentran los tubos guía debido a que en deforman mucho el flujo respecto de los cálculos con
PUMA y la distribución de importancia cambia. Dado que los estado sin barras ni tubos guía ajustan bien, pretendemos estudiar que sucede al introducir
solamente una barra.
Figura 4.28: Distribución de potencias para los casos de inserción de solo 1 barra. De arriba a abajo,
de izquierda a derecha, casos de barra 1, 2, 3 y 4 respectivamente.
En las Figs. 4.29, 4.30, 4.31 y 4.32 observamos las comparaciones realizadas
con PUMA. Vemos que la diferencia en la distribución de potencia es grande
(si comparamos con los resultados obtenidos anteriormente).
En la Tabla 4.4 vemos que en todos los casos kef f en PUMA es mayor que

Barra 1
Barra 2
Barra 3
Barra 4
PARCS
1.08143
1.08252
1.07926
1.08088
PUMA PUMA-PARCS (mk)
1.08192
0.49
1.08356
1.05
1.08231
3.05
1.08243
1.08
Tabla 4.4: Comparación de los resultados obtenidos con PARCS y PUMA.
lo obtenido en PARCS donde obtenemos pesos de del orden de 2 veces mayores. Confirmamos así que el modelo usado para las barras de control presenta
discrepancias no aceptables.
Figura 4.29: Comparación entre la distribución de potencia de PARCS y PUMA para la barra 1.

Figura 4.30: Comparación entre la distribución de potencia de PARCS y PUMA para la barra 2.
Figura 4.31: Comparación entre la distribución de potencia de PARCS y PUMA para la barra 3.

Figura 4.32: Comparación entre la distribución de potencia de PARCS y PUMA para la barra 4.

4.5.
Geometría hexagonal
El núcleo de Atucha 2 tiene geometría hexagonal, por este motivo es lógico modelarlo con esta geometría. Dado que para la geometría cartesiana los resultados ya fueron contrastados contra PUMA, contrastamos los nuevos resultados
obtenidos aquí, contra los obtenidos utilizando geometría cartesiana.
4.5.1.
Núcleo fresco
En este caso usamos las mismas condiciones que en el caso de núcleo fresco
con geometría cartesiana. Las equivalencias geométricas se muestran en el capítulo 3. Los cálculos se realizaron utilizando el método TPEN4 sin utilizar la
corrección por ADF.
Figura 4.33: Distribución de potencia obtenida con el método TPEN.
Los resultados para kef f son para la geometría hexagonal kef fHEX = 1,08446
y para la cartesiana kef fN EM = 1,08470. Tanto para la distribución de potencia
como para el kef f los resultados son razonablemente buenos y el tiempo de
cálculo es mucho menor.
4
Triangular Polinomial Expansion Nodal ver capítulo 2.

Figura 4.34: Comparación entre los resultados obtenidos con las geometrías hexagonal y cartesiana.

4.5.2.
Núcleo con tubos guía
En geometría cartesiana el trozo de la barra de control que atraviesa cada plano
es representado por 4 nodos, en cambio en geometría hexagonal es representado sólo por 1 nodo. Así, tenemos menor libertad al momento de elegir la
posición de la barra en cada plano. Supongamos que el círculo sombreado de
la Fig. 4.35 representa un trozo de barra de control en ese plano, en el modelo
de geometría cartesiana la barra se representaría cómo si afectase a los nodos
16, 17, 22 y 23, pero en geometría hexagonal deberemos elegir si afecta al nodo
formado por 15, 16, 21 y 22 o al nodo formado por 17, 18, 23 y 24.
Figura 4.35: Esquema de distribución de la barra de control en un plano.
Al transformar las barras de la geometría hexagonal a la cartesiana el criterio usado fue: si en el caso de la figura la barra atravesase los nodos 9, 10,
15 y 16, entonces para la geometría hexagonal la representación de este trozo
será el canal5 formado por 15, 16, 21 y 22. Si en cambio la barra se encuentra
en el caso representado en la figura, es decir, la barra ocupa dos nodos de cada
canal, entonces en la geometría cartesiana se usará el canal de la izquierda (en
este caso el formado por 15, 16, 21 y 22).
En la Fig. 4.36 observamos la distribución de potencia obtenida para este
caso, donde kef f = 1,04514, que difiere del kef f calculado con el método NEM
en geometría cartesiana en ≈ 1 mk. En la Fig. 4.37 observamos la diferencia en
la distribución de potencia calculada con TPEN respecto de la calculada con
el método NEM en geometría cartesiana, vemos que esta figura se asemeja a
obtenida en la misma comparación realizada en la sección anterior, excepto
que aquí tenemos mayores discrepancias en la parte derecha del núcleo. Esto se puede explicar debido a cómo modelamos las barras en esta geometría,
donde éstas están levemente corridas hacia la izquierda respecto del modelo
cartesiano, esto explica un desbalance de potencia hacia la derecha.
5
Llamaremos canal a la agrupación de 4 nodos del mismo color.

Figura 4.36: Distribución de la potencia para el modelo con tubos guías
Figura 4.37: Variación de la potencia calculada con el método TPEN en geometría hexagonal respecto
de la calculada con el método NEM en geometría cartesiana.

4.6.
Análisis de transitorios
Una de las características más importantes de PARCS es que puede realizar
cálculos de cinética 3D6 . Aún cuando no disponemos datos para contrastar
nuestros resultados ni tampoco poseemos los parámetros cinéticos característicos de Atucha 2, realizaremos algunos cálculos utilizando parámetros cinéticos
típicos de un núcleo de uranio natural. Para el análisis de transitorios —como
explicamos anteriormente— PARCS resuelve el problema de transitorio con
fuente fija. Primero se resuelve el estado estacionario y a partir de aquí se resuelve el problema del transitorio. Debido a la ventaja en el tiempo de cálculo
decidimos utilizar la geometría hexagonal. El modelo de núcleo es el modelo
de núcleo fresco con geometría caliente y barras de control. Para la evolución
del transitorio solo consideraremos la variación de reactividad debida al movimiento de las barras.
4.6.1.
SCRAM
Analizamos primero un caso de SCRAM. Partimos de un estado estacionario
con todas las barras afuera y en un tiempo t = 0 s se produce un SCRAM por
la inserción completa del banco G30 que consta de las barras 2, 8 y 14 y corresponde a una reactividad negativa de 0,9 $. El tiempo usado en la inserción de
las barras es de 3 s.
t = 0.1 s
t = 0.01 s
t = 0.001 s
Figura 4.38: Evolución temporal de la potencia en un SCRAM para distintos pasos de tiempo.
6
En realizad PARCS puede realizar cálculos de dinámica 3D pero en la jerga a estos códigos
se le llaman de cinética 3D.

En este transitorio usamos el método de Crank-Nicholson sin transformada exponencial para la discretización temporal. En todos los casos a los 3,5 s
se aumentó el paso de tiempo 10 veces. Vemos cómo luego de completada la
extracción de las barras (a los 3 s) podemos aumentar el paso de tiempo obteniendo la misma convergencia. Podemos observar en las referencias de la
figura los pasos temporales utilizados en cada caso, vemos que para un paso
t = 0,01 s el resultado converge. En las Figs. 4.39 y 4.39 vemos cómo evoluciona
la distribución de potencia del núcleo mientras el reactor se va apagando.


Figura 4.39: Evolución temporal de la potencia durante el SCRAM.

Figura 4.40: Evolución temporal de la potencia durante el SCRAM.
4.6.2.
Eyección de BC
Uno de los mayores problemas en el cálculo de reactores es la eyección de una
barra de control. Este es un transitorio sumamente asimétrico donde se generan fuertes desbalances de potencia locales. En este transitorio partimos de
un estado estacionario con todas las barras completamente insertadas y eyectamos la barra 2 desde su posición de 50 % de inserción lo que corresponde
a una inserción de reactividad de 0,4 $. Los problemas fueron simulados con
distintos métodos, obteniéndose el mejor resultado con el método de CrankNicholson con transformada exponencial.
Eyeccion de Barra 2
Potencia normalizada
1.2
1.15
1.1
1.05
t = 0.0001s
t = 0.001s
t = 0.01s
t = 0.1s
1
0.2
0.4
0.6
0.8
1
1.2
Tiempo (seg)
1.4
1.6
1.8
2
Figura 4.41: Evolución temporal de la potencia ante la eyección de la barra 2.
En la Fig. 4.41 observamos la evolución de la potencia en los primeros
segundos. Las líneas continuas corresponden a cálculos realizados aplicando
Crank-Nicholson con la transformada exponencial y las discontinuas a cálculos sin la transformada exponencial. En las referencia de la figura están los
pasos temporales con que se corrió cada caso. Observamos que ese caso converge para un paso de tiempo t = 0,001 s con un error pequeño. En la Fig.
4.42 podemos apreciar cómo evoluciona la distribución de potencia del núcleo
durante el transitorio.


Figura 4.42: Evolución temporal de la potencia para en la eyección de la barra 2.
C APÍTULO V
Conclusiones
Estudiamos los modelos y métodos numéricos involucrados en el código neutrónico de cálculo de núcleo de cinética 3D PARCS y confeccionamos un modelo del núcleo de la Central Nuclear Atucha 2 para geometría cartesiana y
hexagonal. Dado que debimos realizar numerosas comparaciones con los resultados del código PUMA y que nuestro modelo se basó en el utilizado en
PUMA, para transformar la gran cantidad de datos de secciones eficaces de referencia, secciones eficaces incrementales y geometría de barras, desarrollamos
software para la migración automática del formato PUMA al formato PARCS.
Para esto debimos estudiar el formato utilizado por PUMA y la forma en que
éste trata los datos de entrada. Además debimos analizar y comparar gran
cantidad de datos de salida del código PARCS y del código PUMA, para esto
desarrollamos software necesario para tratamiento de los datos y software para la comparación y presentación de los resultados. Analizamos distintos casos
comparando las diferencias en los resultados obtenidos con los distintos métodos de cálculo. Realizamos gran cantidad de comparaciones entre PUMA y
PARCS algunas de las cuales se presentan en este trabajo. En particular realizamos un estudio minucioso del modelo con barras de control y la forma de
migrar los datos de PUMA a PARCS.
Como resultado de lo realizado, podemos cerrar este trabajo con las siguientes conclusiones:
Alcanzamos nuestro objetivo principal que consistía en desarrollar un
modelo de un caso transitorio 3D del núcleo de Atucha 2. Por no poseer
las secciones eficaces para distintos estados del reactor (distintas condiciones de temperatura de combustible, temperatura del moderador, densidad del moderador, etc.) no pudimos implementar el modelo con realimentación para la simulación de casos de dinámica 3D, pero a partir del
modelo desarrollado esta implementación es directa.
En los casos sin el modelo de barras de control los resultados de distribución de potencia obtenidos con PARCS ajustan con PUMA en el orden del
5 % del error relativo. De la misma manera los resultados obtenidos para
los kef f son muy buenos para todos los métodos de cálculo (con ajustes
menores a 0,5mk).
En los casos donde se modelan la barras de control los ajustes con PUMA
no son buenos. Este problema se estudió exhaustivamente haciendo un
análisis de cada parámetro del modelo, sin encontrar la fuente del error.
Podemos asegurar que el error no se debe a el modelado geométrico. En
cuanto al tratamiento de las secciones eficaces incrementales por parte
los códigos PUMA y PARCS, éste es el mismo y no debería ser la causa
del problema. La única inconsistencia que se encontró, es que las secciones eficaces incrementales calculadas por NA-SA son sensiblemente
mayores que las calculadas por la gente de la Universidad de Purdue. Si
bien unas fueron calculadas con DRAGON y otras con HELIOS el orden
de la discrepancia no puede justificarse por este motivo ya que el modelo
utilizado para el cálculo de las secciones eficaces incrementales es básicamente el mismo. Sin duda encontrar el origen de estas discrepancias
ayudará a dilucidar el problema.
Corrimos casos transitorios que evolucionan cualitativamente de manera
acorde con la física de cada transitorio en particular. Sin embargo, hasta
no solucionar el problema de las barras de control, estos resultados no se
pueden considerar confiables.

A PÉNDICE A
Evaluación del Proyecto
En cumplimiento de los requisitos establecidos para la presentación de Proyecto Integrador realizamos la evaluación del proyecto y el análisis económico.
A.1.
Organización del trabajo
En agosto de 2006 el objetivo final del trabajo consistía en desarrollar los conocimientos necesarios para utilizar un código de cálculo neutrónico para ser
implementado en el desarrollo de un simulador de una Central Nuclear Argentina. Así, definimos como un hito del proyecto el desarrollo de este conocimiento que a la vez, debido a la corta duración del proyecto, es el final del
mismo.
Durante el desarrollo del proyecto los objetivos cambiaron según las necesidad de modelar Atucha 1 ó Atucha 2 y según el código de cálculo a utilizar.
Finalmente utilizamos PARCS en el modelado de Atucha 2 y en la Fig. A.1
mostramos cómo fue la organización del proyecto en lo que se asemeja a un
diagrama de Gantt. Debido al carácter de investigación que hay en este proyecto un diagrama de este tipo no puede realizarse a priori dado que solo se
conoce el objetivo final y no, cómo el mismo va a desarrollase.
A.2.
Análisis Económico
Este proyecto se desarrolló en el grupo DIFRA bajo la dirección del Ingeniero
Aníbal Blanco. Para a las comparaciones realizadas con el código PUMA se
consultó al Licenciado Oscar Serra quién además realizó cálculos específicos
para este proyecto. En octubre de 2006 se viajó a un seminario para aprender
la utilización del código PARCS. Además de realizaron consultas vía correo
electrónico a los desarrolladores del código con quién se mantuvo dos reuniones en abril de 2007. Para el desarrollo de los modelos se usaron secciones
eficaces calculadas por NA-SA.
Para realizar el trabajo se utilizó una computadora cuyo costo es de 4700 $,
el programa PARCS nos fue cedido para uso académico. Realizamos un balan-
Persona
Horas Costo por hora ($) Costo total ($)
Ing. Aníbal Blanco
60
50
3000
Lic. Oscar Serra
50
50
2500
Ing. Andrew Ward
10
100
1000
Joaquín Basualdo
400
5
2000
Total
8500
Tabla A.1: Costos principales de recursos humanos.
Ítem
Costo ($)
Personal
8500
Computadora
1500
Seminario SUNCOP
2600
Reunión abril 2007
1000
Costo Total
13600
Tabla A.2: Costos principales del proyecto.
ce grueso de los costos estimados del proyecto. En la tabla A.1 desagregamos
los costos correspondientes ítem Personal. En la Tabla A.2 hacemos un balance
de los costos del proyecto. El resto de los costos se completan en la Tabla A.2.
En este análisis de costos no se tuvo en cuenta la tasa de descuento.


!
"
#$
%""
#&
'(
)""
*(
(,
"
(,"
Figura A.1: Diagrama de la organización del proyecto.
(
+
1
(-
-
+- )-
/-
!0
-"
!$
.
"
"
A PÉNDICE B
Documentación del código
PARCS
A continuación dejamos documentados algunas entradas de los modelos utilizados. En algunos casos se agregan algunos comandos extra que pueden ser
didácticos y en otros se recorta parte del código que puede resultar redundante, como ser el caso de la definición de planos axiales o la definición de la
geometría de cada barra.
B.1.
Núcleo fresco con corrección de ADF en geometría cartesiana
!*********************
CASEID nucleo_fresco
Atucha II sin barras
!*********************
CNTL
core_type PWR
core_power 100.0
th_fdbk F
!-----------------------------------------------------------------------------depletion
T 1.0e-3 F
!
TREE,nset,adf,xes,ene,j1f,chi,chd,vel,det,yld,cdf,gff,bet,lam,dht
TREE_XS
T
7
T
F
F
F
T
F
F
F
F
F
F
T
T
F
!-----------------------------------------------------------------------------!
input iteration
Planar
adj
!
edit
table
power
pin
reac
print_opt
T
T
T
F
F
!
fdbk
flux
Planar
!
rho
precurs
flux
Xe
T/H
print_opt
T
F
F
F
F
!
1d
pk
rad pwr
rad flux
assy
!
const
data
shape
shape
const
print_opt
F
F
F
F
F
!*********************
PARAM
nodal_kern NEMMG !el default es hybrid
! nodal_kern FDM
eps_anm 5.0
!para forzar el uso de NEM cuando nodal_kern es hybrid
n_iters
2 500 !default is 1 500
nspn 1
!default (por difusion, el otro es SP3)
init_guess 0
!coseno (el default es 1-flat)
nlupd_ss 4 4 1
!con esto hay que jugar y ver el optimo
!**********************
TH
fa_powpit 1.181619
!2160/(451 x 4 + 24)
gamma_frac 0.02
unif_th 1.11018 600.45 300.45
FLU_TYP 1
!usa las constantes de agua pesada
!**********************
La tarjeta GEOM define la geometría del núcleo en los casos de geometría
cartesiana y cilíndrica. En este input en particular en la primera matriz vemos
la definición de los reflectores con 1 y de los combustibles con 2 y 3 pero en
realidad sólo la composición 3 corresponde a combustible y la composición 2
si bien el código lo tomará como combustible por ejemplo para el cálculo de la
potencia nominal (que se calcula como el primer valor de fa_powpit por el
número de combustibles) es en realidad reflector. La necesidad de hacer esto es
que de otra manera el método de resolución no funciona. Esto fue consultado
a los autores del código quienes dijeron que este es un tema pendiente y por el
momento ellos también usan el modelo de esta manera.
GEOM
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
geo_dim 50
rad_conf
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 1
0 0 0 0 0 1 1
0 0 0 0 1 1 1
0 0 0 0 1 1 1
0 0 0 1 1 1 1
0 0 1 1 3 3 3
0 0 1 1 3 3 3
0 1 1 3 3 3 3
0 1 1 3 3 3 3
1 1 3 3 3 3 3
1 1 3 3 3 3 3
1 3 3 3 3 3 3
1 3 3 3 3 3 3
1 1 3 3 3 3 3
1 1 3 3 3 3 3
1 3 3 3 3 3 3
1 3 3 3 3 3 3
3 3 3 3 3 3 3
3 3 3 3 3 3 3
1 3 3 3 3 3 3
1 3 3 3 3 3 3
1 1 3 3 3 3 3
1 1 3 3 3 3 3
1 3 3 3 3 3 3
1 3 3 3 3 3 3
3 3 3 3 3 3 3
3 3 3 3 3 3 3
1 2 2 2 2 3 3
1 2 2 2 2 3 3
1 1 2 2 3 3 3
1 1 2 2 3 3 3
1 1 1 3 3 3 3
1 1 1 3 3 3 3
1 1 3 3 3 3 3
1 1 3 3 3 3 3
0 1 1 3 3 3 3
0 1 1 3 3 3 3
0 0 1 1 3 3 3
0 0 1 1 3 3 3
0 0 0 1 1 1 1
0 0 0 0 1 1 1
0 0 0 0 1 1 1
0 0 0 0 0 1 1
0 0 0 0 0 0 1
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
grid_x
neutmesh_x
grid_y
neutmesh_y
grid_z
boun_cond
58
0
0
0
0
0
0
1
1
1
1
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
1
1
1
1
0
0
0
0
0
0
28
4
4
!nasyx,nasyy,nz,nrb,nrt
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 1 1
0 0 0 0 0 1 1 1 1
0 0 0 1 1 1 1 1 1
0 1 1 1 1 1 1 1 3
1 1 1 1 1 1 1 1 3
1 1 1 1 1 3 3 3 3
1 1 1 1 1 3 3 3 3
3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3
1 1 1 3 3 3 3 3 3
1 1 1 3 3 3 3 3 3
1 1 1 1 1 1 3 3 2
0 1 1 1 1 1 3 3 2
0 0 0 1 1 1 1 1 1
0 0 0 0 0 1 1 1 1
0 0 0 0 0 0 0 1 1
0 0 0 0 0 0 0 0 0
50*13.619
50*1
58*11.7944
58*1
4*12.05 20*26.535
2 2 2 2 2 2
0
1
1
1
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
2
2
2
2
1
1
1
0
1
1
1
1
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
2
2
2
2
1
1
1
1
1
1
1
1
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
2
2
1
1
1
1
1
1
1
1
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
1
1
1
1
1
1
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
1
1
1
1
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
1
1
1
1
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
1
1
1
1
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
1
1
1
1
1
1
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
1
1
1
1
1
1
1
1
2
2
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
1
1
1
1
1
1
1
1
2
2
2
2
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
1
1
1
1
0
1
1
1
2
2
2
2
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
1
1
1
0
0
1
1
1
2
2
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
1
1
1
0
0
1
1
1
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
1
1
1
1
1
0
0
0
1
1
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
1
1
1
1
0
0
0
0
1
1
1
1
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
1
1
1
1
0
0
0
0
0
1
1
1
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
1
1
1
1
1
0
0
0
0
0
0
1
1
1
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
1
1
1
1
1
0
0
0
0
0
0
0
1
1
1
1
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
1
1
1
1
0
0
0
0
0
0
0
0
1
1
1
1
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
1
1
1
1
0
0
0
0
0
0
0
0
0
1
1
1
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
1
1
1
0
0
0
0
0
0
0
0
0
0
0
1
1
1
1
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
1
1
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
1
1
1
1
1
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
1
1
1
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
1
1
1
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
1
1
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
1
1
3
3
3
3
3
3
3
3
3
3
2
2
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
1
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
1
1
3
3
3
3
3
3
2
2
2
2
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
1
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
1
1
1
3
3
1
1
2
2
2
2
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
1
1
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
2
2
3
3
3
3
1
1
3
3
3
3
3
3
1
1
3
3
1
1
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
3
3
1
1
1
1
1
1
3
3
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
4*8.6
!ibcw,ibce,ibcn,ibcs,ibcb,ibct
planar_reg 1
!AQUI SE DEBE DEFINIR DE LA MISMA MANERA QUE EN planar_reg 2 PERO CON COMPOSICIONES DISTINTAS POR EJEMPLO TODOS 1

En planar_reg 2 definimos los planos axiales que corresponden a la longitud activa. El porque de el uso de tantas composiciones se debe al ADF como
se explicó en la sección 4.1.2.
planar_reg 2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
3
5
2
2
2
2
2
2
3
5
2
2
2
2
2
2
2
2
2
2
2
2
3
5
2
2
3
5
4
6
3
5
2
2
3
5
4
6
2
2
2
2
2
2
2
2
2
2
2
2
2
2
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
2
2
2
2
2
2
3
5
2
2
2
2
2
2
2
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
2
2
2
2
3
5
4
6
3
5
2
2
2
2
2
2
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
2
2
3
5
4
6
3
5
4
6
3
5
2
2
2
2
2
2
2
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
2
2
2
2
2
2
2
2
2
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
2
2
2
2
2
2
2
2
2
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
2
2
2
2
2
2
2
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
2
2
2
2
2
2
2
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
2
2
2
2
2
2
2
2
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
2
2
2
2
2
2
2
2
2
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
2
2
2
2
2
2
2
2
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
2
2
2
2
2
2
2
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
2
2
2
2
2
2
2
2
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
2
2
2
2
2
2
2
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
2
2
2
2
2
2
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
2
2
2
2
2
2
2
2
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
2
2
2
2
2
2
2
2
2
2
2
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
2
2
2
2
2
2
2
2
2
2
2
2
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
2
2
2
2
2
2
2
2
2
2
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
2
2
2
2
2
2
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
2
2
2
2
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
2
2
2
2
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
2
2
2
2
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
2
2
2
2
2
2
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
2
2
2
2
2
2
2
2
2
2
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
2
2
2
2
2
2
2
2
2
2
2
2
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
2
2
2
2
2
2
2
2
2
2
2
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
2
2
2
2
2
2
2
2
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
2
2
2
2
2
2
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
2
2
2
2
2
2
2
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
2
2
2
2
2
2
2
2
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
2
2
2
2
2
2
2
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
2
2
2
2
2
2
2
2
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
2
2
2
2
2
2
2
2
2
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
2
2
2
2
2
2
2
2
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
2
2
2
2
2
2
2
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
2
2
2
2
2
2
2
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
2
2
2
2
2
2
2
2
2
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
2
2
2
2
2
2
2
2
2
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
2
2
2
2
2
2
2
4
6
3
5
4
6
3
5
4
6
2
2
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
2
2
2
2
2
2
4
6
3
5
4
6
2
2
2
2
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
2
2
2
2
2
2
2
4
6
2
2
2
2
2
2
4
6
3
5
4
6
3
5
4
6
3
5
4
6
3
5
4
6
2
2
2
2
2
2
2
2
2
2
2
2
2
2
3
5
4
6
2
2
4
6
3
5
4
6
2
2
4
6
2
2
2
2
2
2
2
2
2
2
2
2
4
6
2
2
2
2
2
2
4
6
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
planar_reg 3
!AQUI SE DEBE DEFINIR DE LA MISMA MANERA QUE EN planar_reg 2 PERO CON COMPOSICIONES DISTINTAS POR EJEMPLO TODOS 7
pr_assign 4*1 20*2 4*3
!******************************************************************************
En la tarjeta DEPL se llama a los archivos PMAX. Más adelante daremos un
ejemplo del formato PMAX.
DEPL
!
Index
PMAXS File Name
Br_struct
PMAXS_F 1 ’./xsec_mio/end_inf.PMAX’
1
PMAXS_F 2 ’./xsec_mio/reflect.PMAX’
2
PMAXS_F 3 ’./xsec_mio/fuel_NW.PMAX’
3
PMAXS_F 4 ’./xsec_mio/fuel_NE.PMAX’
4
PMAXS_F 5 ’./xsec_mio/fuel_SW.PMAX’
5
PMAXS_F 6 ’./xsec_mio/fuel_SE.PMAX’
6
PMAXS_F 7 ’./xsec_mio/end_sup.PMAX’
7
!******************************************************************************
.

B.2.
SCRAM en núcleo fresco con geometría hexagonal
!*********************
CASEID scram_bancoG30 Atucha II con barras modelo hexagonal
!*********************
CNTL
core_type PWR
core_power 100.0
th_fdbk
F
search keff
transient T
!
#1 #2 #3 #4 #5 #6 #7 #8 #9 #10 #11 #12 #13 #14 #15 #16 #17 #18
!
barras totalmente insertadas:
!
bank_pos 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0
!
barras totalmente extraidas:
bank_pos 570 573 596 561 588 570 581 575 591 560 588 570 573 577 592 573 575 565
!-----------------------------------------------------------------------------depletion
T 1.0e-3 F
En TREE_XS debemos modificar las opciones para que lea los parámetros
cinéticos del archivo PMAX.
!
TREE,nset,adf,xes,ene,j1f,chi,chd,vel,det,yld,cdf,gff,bet,lam,dht
TREE_XS
T
5
F
F
F
F
T
F
T
F
F
F
F
T
T
F
!-----------------------------------------------------------------------------!
input iteration
Planar
adj
!
edit
table
power
pin
reac
print_opt
T
T
T
F
F
!
fdbk
flux
Planar
!
rho
precurs
flux
Xe
T/H
print_opt
F
F
F
F
F
!
1d
pk
rad pwr
rad flux
assy
!
const
data
shape
shape
const
print_opt
F
F
F
F
F
!*********************
PARAM
nodal_kern TPEN !el default es hybrid, esto se puede probar a ver cual funciona mejor
!
nodal_kern FDM !el default es hybrid, esto se puede probar a ver cual funciona mejor
n_iters
2 500
!default is 1 500
nspn 1
!default (por difusion, el otro es SP3)
init_guess 0
!coseno (el def es 1-flat)
nlupd_ss 4 4 1
!con esto hay que jugar y ver el optimo
!**********************
TH
fa_powpit 1.166307
gamma_frac 0.02
unif_th 1.11018 600.45 300.45
FLU_TYP 1
!******************************************************************************
GEOMHEX
geo_dim
14 28 4 4
!nring, nz, refl bot, refl top
rad_conf
360
!full rotation symmetry
1 1 1 1 1
1 1 1 1 2 2 1 1 1 1
1 1 1 1 2 2 2 3 2 1 1 2 1 1 1
1 1 1 2 2 3 3 3 3 2 1 2 2 2 1 1
1 1 2 2 2 3 3 3 3 3 3 2 2 3 3 2 2 1 1
1 1 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2 1 1
1 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2 2 1
1 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2 1
1 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2 1
1 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2 1 1
1 1 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2 1 1 1
1 1 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2 1 1 1 1
1 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2 2 2 1
1 1 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2 1 1
1 1 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2 1 1
1 1 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2 1 1
1 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2 1
1 1 1 1 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2 1 1
1 1 1 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2 1 1
1 1 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2 1
1 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2 1
1 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2 1
1 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2 2 1
1 1 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2 1 1
1 1 2 2 3 3 2 2 3 3 3 3 3 3 2 2 2 1 1
1 1 2 2 2 1 2 3 3 3 3 2 2 1 1 1
1 1 1 2 1 1 2 3 2 2 2 1 1 1 1
1 1 1 1 2 2 1 1 1 1
1 1 1 1 1
grid_hex
27.24 1
! distancia entre caras (cm)
grid_z
4*11.625 20*26.535 4*8.75
! 530.7/20 = 26.535

assy_type
assy_type
assy_type
albedo_r
albedo_zb
albedo_zt
1 4*1 20*2 4*3
2 4*1 20*4 4*3
3 4*1 20*5 4*3
0.5 0.5
0.5 0.5
0.5 0.5
REFL
FUEL
FUEL
Para ser ordenados leemos las barras de el archivo barras_hex.bar
file
crb_def
barras_hex.bar
18
1
1
2 284.57 569.15
2
3
4 286.34 572.68
3
5
6 297.62 595.23
4
7
8 280.29 560.57
5
9 10 293.79 587.59
6 11 12 284.96 569.92
7 13 14 290.20 580.40
8 15 16 287.09 574.18
9 17 18 295.45 590.89
10 19 20 279.98 559.95
11 21 22 293.79 587.59
12 23 24 284.96 569.92
13 25 26 286.34 572.68
14 27 28 288.22 576.44
15 29 30 295.98 591.95
16 31 32 286.34 572.68
17 33 34 287.09 574.18
18 35 36 282.20 564.40
crb_type
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
!******************************************************************************
TRAN
time_step 10 .1 3.5 10
!
EXPO_OPT
t T
move_bank 2 0 573 3 0
move_bank 8 0 575 3 0
move_bank 14 0 577 3 0
!******************************************************************************
DEPL
!
Index
PMAXS File Name
Br_struct
PMAXS_F 1 ’./xsec_mio/end_inf.PMAX’
1
PMAXS_F 2 ’./xsec_mio/reflect.PMAX’
2
PMAXS_F 3 ’./xsec_mio/end_sup.PMAX’
3
PMAXS_F 4 ’./xsec_mio/fuel.PMAX’
4
PMAXS_F 5 ’./xsec_mio/fuel.PMAX’
5
!******************************************************************************
.
B.2.1.
Archivo barras_hex.bar
Cualquier parte de la entrada de PARCS se puede llamara mediante la opción file, en particular lo hacemos con las barras pues el modelado es siempre el mismo y representan muchas líneas de código. Tengamos en cuenta que
en la geometría cartesiana el número de nodos que definen una barra se multiplica por 4 dando origen a archivos mucho mayores.
custom_cr 18
ccr_bank -1 20 37
4.474881e+001 1
490
7.100817e+001 1
113
9.930273e+001 1
296
1.216132e+002 1
296
1.509835e+002 1
498
1.805033e+002 1
104
2.042910e+002 1
104
2.338966e+002 1
304
2.635519e+002 1
489
2.878152e+002 1
489
3.174538e+002 1
112
3.471246e+002 1
295
3.716155e+002 1
295
4.012530e+002 1
497
4.309165e+002 1
103
4.555396e+002 1
103
4.851688e+002 1
303
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
1.00e+000
1.00e+000
1.00e+000
1.00e+000
1.00e+000
1.00e+000
1.00e+000
1.00e+000
1.00e+000
1.00e+000
1.00e+000
1.00e+000
1.00e+000
1.00e+000
1.00e+000
1.00e+000
1.00e+000

5.148207e+002 1
488 22
5.395297e+002 1
488 23
5.691496e+002 1
111 24
ccr_bank -1 20 37
! ...
! ...
!DE LA MISMA MANERA SE DEFINE
B.3.
1.00e+000
1.00e+000
1.00e+000
LA GEOMETRÍA DE LAS DEMÁS 17 BARRAS
Ejemplo de un archivo PMAX
Este archivo corresponde a una composición de combustible para una geometría hexagonal. En este formato es importante respetar los espacios y los
formatos de los números.
GLOBAL_V
1 2 6 6 1 1
1 1 F F F F T F T F F F F T T F T
Contents of T/H Invariant Variabarales(TIV) block and Cross Sections(XS) block
TIV:Chi,inV/Bet/Lam/
XS:tr,ab,nf,kf/sct/
2 Group value of each variable are put together in a line.
Some variables(separated by ",") share a line,"/" means change line
STA_VAR
4 CR DC PC TF
BRANCHES
1
37
0
0
0
RE
1
0.00000
1.11018
0.00000
973.6000
Aquí definimos las 37 composiciones de secciones eficaces incrementales
que corresponden a las 18 barras y al tubo guía.
CR
1
1.00000
1.11018
0.00000
973.6000
CR
2
2.00000
1.11018
0.00000
973.6000
CR
3
3.00000
1.11018
0.00000
973.6000
CR
4
4.00000
1.11018
0.00000
973.6000
CR
5
5.00000
1.11018
0.00000
973.6000
CR
6
6.00000
1.11018
0.00000
973.6000
CR
7
7.00000
1.11018
0.00000
973.6000
CR
8
8.00000
1.11018
0.00000
973.6000
CR
9
9.00000
1.11018
0.00000
973.6000
CR
10
10.00000
1.11018
0.00000
973.6000
CR
11
11.00000
1.11018
0.00000
973.6000
CR
12
12.00000
1.11018
0.00000
973.6000
CR
13
13.00000
1.11018
0.00000
973.6000
CR
14
14.00000
1.11018
0.00000
973.6000
CR
15
15.00000
1.11018
0.00000
973.6000
CR
16
16.00000
1.11018
0.00000
973.6000
CR
17
17.00000
1.11018
0.00000
973.6000
CR
18
18.00000
1.11018
0.00000
973.6000
CR
19
19.00000
1.11018
0.00000
973.6000
CR
20
20.00000
1.11018
0.00000
973.6000
CR
21
21.00000
1.11018
0.00000
973.6000
CR
22
22.00000
1.11018
0.00000
973.6000
CR
23
23.00000
1.11018
0.00000
973.6000
CR
24
24.00000
1.11018
0.00000
973.6000
CR
25
25.00000
1.11018
0.00000
973.6000
CR
26
26.00000
1.11018
0.00000
973.6000
CR
27
27.00000
1.11018
0.00000
973.6000
CR
28
28.00000
1.11018
0.00000
973.6000
CR
29
29.00000
1.11018
0.00000
973.6000
CR
30
30.00000
1.11018
0.00000
973.6000
CR
31
31.00000
1.11018
0.00000
973.6000
CR
32
32.00000
1.11018
0.00000
973.6000
CR
33
33.00000
1.11018
0.00000
973.6000
CR
34
34.00000
1.11018
0.00000
973.6000
CR
35
35.00000
1.11018
0.00000
973.6000
CR
36
36.00000
1.11018
0.00000
973.6000
CR
37
37.00000
1.11018
0.00000
973.6000
XS_SET 00000001 1 1 1 1 1 0 0.00000 0.00000 0.00000 0.55539 1.11018 0.00000 0.00000 0.00000
HISTORYC
1
0.00000
1.11018
0.00000
973.60000
1.00000E+00 0.00000E+00 1.04118e-07 2.43278e-06
0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00
0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00
REFE
1
1
+2.38489E-01+3.45100E-01+1.86891E-03+4.12283E-03+8.66857E-04+5.19614E-03+1.05976E-14+6.89024E-14
+0.00000E+00+0.00000E+00+8.25222E-03+0.00000E+00
BRCR
1
1
+1.14510E-03-1.41461E-03+2.75588E-03+7.31242E-03-4.31441E-05+5.64911E-04-5.06845E-16+7.06180E-15
+0.00000E+00+0.00000E+00-7.98679E-04+0.00000E+00

BRCR
2
1
+2.73410E-03-6.86623E-04+2.04452E-03+6.03067E-03-4.21595E-05+5.30605E-04-4.95230E-16+6.62865E-15
+0.00000E+00+0.00000E+00-7.23671E-04+0.00000E+00
BRCR
3
1
+1.97766E-03-1.89494E-04+1.77568E-04+2.73640E-03-2.75482E-05+1.92287E-04-3.23855E-16+2.38140E-15
+0.00000E+00+0.00000E+00+5.46558E-05+0.00000E+00
BRCR
4
1
+2.74486E-03-2.01090E-04+2.48630E-04+3.53437E-03-3.56160E-05+2.43326E-04-4.19035E-16+3.01313E-15
+0.00000E+00+0.00000E+00+2.53878E-05+0.00000E+00
BRCR
5
1
+2.05051E-03-1.96474E-04+1.84109E-04+2.83720E-03-2.85630E-05+1.99370E-04-3.35784E-16+2.46912E-15
+0.00000E+00+0.00000E+00+5.66691E-05+0.00000E+00
...
...
De la misma manera se definen las seccione eficaces incrementales para las
restantes 32 composiciones.

Referencias
[1] T. Downar, D. Lee, Y. Xu, and T. Kozlowski. PARCS v2.6 U.S NRC Core
Neutronics Simulator - Theory Manual (Draft), June 2004.
[2] T. Downar, Y. Xu, and V. Seker. PARCS v2.7 U.S NRC Core Neutronics
Simulator User Manual, August 2006.
[3] James J. Duderstadt and Louis J. Hamilton. Nuclear Reactor Analysis. John
Wiley & Sons, 1976.
[4] J. Marconi Giglio, C. Grant, and O. Serra. Updated Methods for PUMA 4
Code Neutron Flux Calculations. Technical report, 2006.
[5] C. Grant, R. Mollerach, F. Leszczynski, O. Serra, J. Marconi, and J. Fink.
Validation of Updated Neutronic Calculation Models Proposed for Atucha II
PHWR. Part II: Benchmark Comparisons of PUMA Core Parameters with
MCNP5 and Improvements Due to a Simple Cell Heterogeneity Correction.
NASA-CNEA, September 2006.
[6] Carlos Grant. Manual del código PUMA versión 4. CNEA, 2004.
[7] CRISSUE-S - WP2 Neutronics/Thermal-hydraulics Coupling in LWR Technology: State of the art Report. NEA, 2004.
[8] CRISSUE-S - WP3 Neutronics/Thermal-hydraulics Coupling in LWR Technology: Achievements and Recommendations Report. NEA, 2004.
[9] Karl O. Ott and Robert J. Neuhold. Introductory Nuclear Reactor Dynamics.
American Nuclear Society, 1985.
[10] R. J .J. Stamm´ler and M. J. Abbate. Methods of Steady-State - Reactor Physics
in Nuclear Design. Academic Press, 1983.
[11] T. M. Sutton. Wielandt Iteration as Applied to the Nodal Expansion Method,
1988.
[12] Cho, J.Y., et al. Hexagonal CMFD Formulation Employing the Triangular Polynomical Expansion Method, September 2001.
[13] P. J. Turinsky et al. NESTLE: A Few-Group Neutron Diffusion Equation Solver
Utilizing the Nodal Expansion Method for Eigenvalue, Adjoint, Fixed-Source
Steady State and Transient Problems, 1994.
[14] Y. Xu and T. Downar. GenPMAX - Code for Generating the PARCS Cross
Section Interface File PMAX, December 2005.
[15] J. Longhino, L. Torres y O. Serra. Cálculos neutrónicos con el código
PUMA y comparación con MCNP para distintas distribuciones de boro
en el moderador del núcleo de Atucha II. Technical report.

Agradecimientos
El agradecimiento es la memoria del corazón.
Siempre y como me enseñaron mis abuelas, primero que a nadie, le agradezco
a Dios por tener tanto y a tantos para agradecer.
Gracias a mi gran familia, a toda (salteños, santiagueños, tucumanos, a todos), especialmente a mi familia metanense (esto incluye a mis buenos amigos)
por estar siempre a la par mía. Gracias por las cartas, las llamadas por teléfono,
por los asados de bienvenida y los de despedida, por los dulces y por los pensamientos.
Yéndonos un poco al sur, gracias a los ib0X con los que compartí en este tiempo, especialmente a ib04; de estos 3 años me llevo incontables buenos
momentos, la verdad, no podía pedir un grupo mejor (en realidad si. . . pero
bueno, es lo que hay ;).
Gracias a todos lo que me ayudaron en este trabajo, gracias a la gente de
DIFRA que siempre me ayudó con la mejor predisposición y muy especialmente gracias a Oscar Serra a quien atormenté casi todo este último semestre.
Gracias a mi dire Aníbal por el aguante (qué plomo de alumno te echaste eh =).
Gracias al profesor Tom Downar y a Andrew Ward por responder amablemente mis consultas.
Gracias a la gente que hace posible este lugar tan especial, el IB, a los profesores que se esfuerzan por enseñarnos algo más, a las secretarias que nos facilitan cualquier trámite, al personal de limpieza en especial a quienes nos arreglaban la habitación cada mañana, al personal de la biblioteca por su buena
onda y su dedicación, a la gente de los talleres, al personal administrativo y
a todos en general. Gracias al pueblo argentino pues todo esto es fruto de su
contribución y gracias a CNEA por apostar a la educación.
Finalmente gracias a todas las personas que me dieron una mano para llegar aquí, si me detengo unos segundos a pensar se me cruzan muchas por la
cabeza y aunque difícilmente me acuerde de todos en este momento, no me
olvido de una palabra de aliento ni de un gesto desinteresado; mi más sincero
agradecimiento.