) } : Dom( ) = { A / } A, } Si x lR Dom( 2) = lR, X …. …… 1 y : y > 0

ℜ2 = { (x, y)∈Ax B / x + y > 1 }
Si x∈lR ⇒ ∃y > 1-x∈lR , y ∈lR ⇒ Dom(ℜ2 ) = lR,
Ran(ℜ2 ) = lR
Funciones en una variable R eal
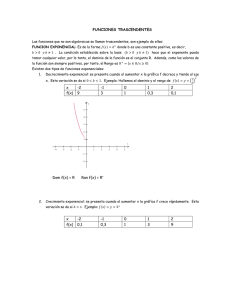
Para aproximar el gráfico realizamos una tabulación:
CÁLCULO DIFERENCIAL E INTEGRAL I
X
y : y > 1-x
….
……
y
1
y:y> 0
….
……
2
y : y > -1
1
….
……
2.1. RELACIONES
EN EL PLANO CARTESIANO.
Definición 2.1. Sean A, B subconjuntos de lR , A x B su producto cartesiano. Diremos que el
2
1
x
conjunto ℜ ⊆ A x B es una relación de A en B si ciertos elementos de A y B satisfacen
proposición verdadera.
ℜ = { (a, b) / a esta en relación con b ( a ℜ b ) }
Dominio de la relación  : Dom(ℜ) = { a∈A / ∃ b ∈ B, a ℜ b }
Rango de la relación  : Ran(ℜ) = Im(ℜ) = ℜ(Dom(ℜ)) = { b ∈B / ∃ a∈A, a ℜ b }
- 25 -
Ejemplo : A = {1, 2, 3, 4, 5 }
y
B = { 1, 2, 3, 4, 5, 6 }
ℜ1 ={(a, b)∈Ax B / b = 2a }
= {(1, 2), (2, 4), (3, 6) }
Ejemplo : A = lR, B = lR
ℜ2 = { (x, y)∈Ax B / x + y > 1 }
•
4
2
⇒ Dom(ℜ1 ) = {1, 2, 3 }
Ran(ℜ1 ) = { 2, 4, 6 }
•
6
•
1 2 3
x
5) Tabulación: Consiste en construir una tabla de valores para x
y. Para esto despejar una
de las variables de E(x, y) = 0 dando valores a la otra de acuerdo a la extensión.
Funciones en una variable R eal
CÁLCULO DIFERENCIAL E INTEGRAL I
6) Trazo del gráfico aproximado en el plano XY : Usamos los pasos 1, 2, 3, 4, 5.
Gráfico
en el
relación
Ejemploaproximado
: Aproximemos
el plano
gráficolRxlR
de ℜ de
= {una
(x, y)
/ E(x, tipo
y) = curva
xy – x (E(x,
+ y = y)
0 }= 0)
Dada una relación ℜ ={(x, y)∈lRxlR/ E(x, y) = 0}. Se quiere los puntos del plano que
1)
a) Intersección
con el eje
X ⇒
E(x, que
0) = uno
-x =de
0 ⇒
x=0
satisfacen
dicha relación
. Cabe
señalar
los objetivos
finales de este curso es poder
b) Intersección
el eje Yespeciales,
⇒ E(0, y)que
= ymás
= 0 adelante
⇒ y = le0 llamaremos funciones.
trazar
el gráfico decon
relaciones
x
2)
Despejandocon
y =los ejes∈Coordenados:
lR sí x ≠ - 1
1) a)
Intersección
x +1
Intersección
con
⇒ Dom(ℜ
) =ellReje
– X;
{-1}en E(x, y) hacer y = 0, hallar los valores de x. Luego los puntos
(x, 0) son los puntos de
y intersección con elyeje X.
y
b)
Intersección
Despejando
conx el
= eje Y;∈enDom(
E(x,ℜ
y)) hacer
⇒ x = 0,
< -hallar
1 ∨ los valores
> - 1 de y. Luego los puntos
y Y.
1− y
(0, y) son los puntos1 −
deyintersección con 1el−eje
⇒ Ran(ℜ) = lR – {1}
3) De
(2)(a) se( Dominio
tiene queyxRango)
= -1 es asíntota vertical.
2)
Extensión
De
(2)(b)
se
tiene
que
y
1 es asíntota
horizontal.
Es el conjunto de valores=reales
que pueden
tomar las riables x e y dependiendo de
4) E(x,
y)esté
≠ E(x,
-y) ⇒laNo
hay simetría
eje X
como
definida
relación
ó hallarrespecto
Dom(ℜ)del
y Ran(
ℜ).
3) Asíntotas a la curva: Vienen a ser las
- 26
rectas
que a medida que se comienzan a alejar del
origen se aproximan a los puntos de la curva.
a) Asíntotas Verticales (x = a): En E(x, y) = 0 despejar y luego hallar todos los valores de x
para los cuales el denominador se anula, estos valores darán asíntotas verticales.
b) Asíntotas Horizontales (y = b): En E(x, y) = 0 despejar x hallar todos los valores de y
para los cuales el denominador se anula los valores de y daran asíntotas horizontales.
4) Simetría de la curva respecto de los ejes y del origen:
a) Simetría respecto del eje X: La curva E(x, y) = 0 es simétrica respecto del eje X si solo
si E(x, -y) = Ex, y).
b) Simetría respecto del eje Y: La curva E(x, y) = 0 es simétrica respecto del eje Y si solo
si E(-x, y) = E(x, y).
c) Simetría respecto del origen: La curva ℜ(x, y) = 0 es simétrica respecto del origen si
solo si E(-x,-y) = E(x, y).
Funciones en una variable R eal
CÁLCULO DIFERENCIAL E INTEGRAL I
E(x, y) ≠ E(-x, y) ⇒ No hay simetría respecto del eje Y
E(x, y) ≠ E(-x, -y) ⇒ No hay simetría respecto del Origen.
5) Tabulación
6) Gráfico
X
….
-2
….
0
….
1
y
x
x +1
…
2
…
0
…
y=
3
2
1
1
-2
2
…
2
…
1
-1
2
x
-1
…
2
3
…
2.2. FUNCIONES ESPECIALES EN UNA VARIABLE REAL .
Definición 2.2. Diremos que una relación f de A en B es una función si satisface:
i) Condición de existencia ∃ y ∈ B / (x, y) ∈ f para algún x ∈ A.
ii) Condición de unicidad sí (x, y1 )∈f ∧ (x, y2 )∈f ⇒ y1 = y2
Definición 2.3. Dos funciones f, g son iguales ⇔ f(x) = g(x), ∀x ∈Dom(f) = Dom(g)
Observación:
1) Para la función f = {(x, y) ∈AxB / x f y ⇔ y = f(x)}.
Denotaremos f : A → B / y = f(x)
Aquí si Dom(f) = A entonces f es llamada aplicación.
2) Si (x, y)∈ f ⇒ y = f(x) se llama imagen de x a través de f.
x se llama pre-imagen de y a través de f.
3) No toda relación es función. Contraejemplo ℜ = { (x, y) ∈lRxlR / x = 2 }. No es función.
No se cumple la condición (ii) pues (2, 1) ∈ℜ ∧ (2, 2 ) ∈ℜ pero 1 ≠ 2.
4) Si A1 ⊆Dom(f) ⇒ f(A1 ) = {y∈B / ∃x∈A1 , f(x) = y} es el conjunto imagen de A1 .
En particular f(Dom(f)) = Ran(f)
5) Si B1 ⊆Ran(f) ⇒ f-1 (B1 ) = {x ∈A / ∃y∈B1 , f(x) = y} es el conjunto imagen inversa de B1 .
En particular f-1 (Ran(f)) = Dom(f)
- 27 -
Funciones en una variable R eal
CÁLCULO DIFERENCIAL E INTEGRAL I
Funciones especiales con gráficos aproximados:
1) Función Constante:
f : lR → lR / f(x) = c (constante).
Dom(f) = lR , Ran(f) = { c }
Sí c = 0 entonces
f se llama función nula.
2) Función Identidad:
1lR : lR → lR / 1lR (x) = x
Dom( 1lR ) = lR
Ran( 1lR ) = lR
4) Función Valor Absoluto:
f : lR → lR / f(x) = | x | =
x sí x ≥ 0
∨
-x sí x < 0
Dom( f ) = lR
Ran( f ) = [ 0, +∞ ⟩
5) Función Máximo Entero:
f : lR → lR / f (x) = [[ x ]]
Dom(f ) = lR
Ran(f ) = Z
6) Función Raíz Cuadrada:
f : lR → lR / f(x) = x
Dom(f) = [ 0, +∞ ⟩
Ran(f) = [ 0, +∞ ⟩
7) Función Signo:
f : lR → lR / f(x) = sig(x) =
-1 Sí x < 0
0 Sí x = 0
1 Sí x > 0
Dom(f) = lR
Ran(f) = { -1, 0, 1 }
2.3. CLASIFICACIÓN DE FUNCIONES.
1) Función restricción: Dada la función f : lR → lR y A ⊂ Dom(f) se dice que h : A → lR
es la restricción de f a A si: h(x) = f(x), ∀ x∈A. Notación: h = f A ó sea y = f(x) ; x ∈A
- 28 -
Funciones en una variable R eal
CÁLCULO DIFERENCIAL E INTEGRAL I
Ejemplo: Si consideramos la función f(x) = x , A = [1, 2] ⊂ Dom(f).
Se tiene la restricción y = f(x) ; x ∈A
Gráfico de f
Gráfico de f A
2) Función traslación: Dada la función y = f(x) y sean h, k∈lR tales que h ≠ 0, k ≠ 0 entonces
la función t(x) = f(x+h)+k es llamada la función traslación de f.
Notar que si x∈Dom(f) entonces x-h∈Dom(t). Si y ∈Ran(f) entonces y-k∈Ran(t).
Por otro lado si h = 0 entonces se tiene traslación en el eje de las ordenadas. Si k = 0 entonces
se tiene traslación en el eje de las abscisas.
Ejemplo: Si consideramos la función f(x) =
x , Dom( f ) = [ 0, +∞ ⟩ , Ran( f ) = [ 0, +∞ ⟩
Para h = 1, k = 1 se tiene la función traslación t(x) = f(x+1)+1 =
x + 1 +1 tal que:
Dom( t ) = [- 1, +∞ ⟩ , Ran( t ) = [1 , +∞ ⟩
3) Función sucesión: Sea K⊆ Z , una función f : K → lR tal que y = f(k) = ak se dice que es
una función sucesión ó simplemente una sucesión. Notaciones: f = (a k)k∈K
Ejemplo: La sucesión (
1
k
) k∈N
ak
•
1
•
1/2
1/3
1
2
•
3
k
4) Función acotada: Una función y = f(x) se dice que es acotada si Ran(f) es acotado. Ó sea
existe k ∈lR tal que |f(x)| ≤ k , ∀x ∈Dom(f).
Ejemplo: La función restricción f(x) = x ; x ∈[1, 2] es acotada pues si 1 ≤ x ≤ 2 entonces -3 ≤
f(x) ≤ 3 entonces existe k = 3 tal que |f(x)| ≤ 3, ∀x∈[1, 2].
5) Función periódica: Sea A ⊂ lR, se dice que f : A → lR es una función periódica sí ∃ p
∈lR, p≠ 0 tal que ∀x∈Dom(f) se tiene i) x+p ∈Dom(f), ii) f(x+p) = f(x)
El número p se denomina periodo de f.
El menor periodo positivo T es llamado periodo fundamental de f.
Ejemplo: f : Z → lR / f(x) = (- 1)x
Dom(f) = Z
Rang(f) = { -1, 1}
Para hallar el periodo se quiere t tal que f(x+t) = (-1) x+ t = (- 1)x = f(x)
(-1) x.( -1)t = (-1) x pero ( -1)x ≠ 0 ∀ x ∈ Z
- 29 -
⇔ ∀ y ∈ B ∃ x ∈ Dom(f) tal que y = f(x) ⇔ Ran(f) = B.
iii) Una función f : A → B es biyectiva(biunívoca) si es inyectiva y sobreyectiva
Funciones en una variable R eal
Ejemplo: La función y = f(x) =
CÁLCULO DIFERENCIAL E INTEGRAL I
x es inyectiva pues si x1 , x2 ∈Dom(f) = [ 0, +∞ ⟩ , f(x1 ) =
x = x = f(x2 ) entonces x1 = x2 .
(-1) 1t = 1 ⇔2 t = 2k, k ∈ Z . Por lo tanto
t = 2k , k ∈Z es periodo de f
Sin
la función
f(x)el=periodo
x2 no esfundamental
inyectiva pues x1 = -1, x2 = 1∈Dom(f) = lR , f(x1 ) =
Paraembargo
k = 1 entonces
T =y 2= es
f(x2 ) pero x1 ≠ x2 .
6) Funciones Pares e Impares: Dada una función f : lR → lR tal que x, -x ∈ Dom(f) es
) ; =x- ∈
par si f(-x) = f(x) e imparsif1 (f(x-x)
f(xA).1
Observación: Si f(x) = 
es función tal que f1 , f2 son inyectivas en A1 , A2
 f 2 ( x ) ; x ∈ A2
4
Ejemplo: f(x) = x , x ∈ lR es función par pues ∀ x ∈ Dom(f) = lR , -x ∈ Dom(f)
respectivamente entonces
f será inyectiva si: Ran(f1 )∩Ran(f2 ) = Φ . Esto se puede generalizar
Además f(-x) = ( -x)4 = (x)4 = f(x)
para funciones con más de dos correspondencias.
Ejemplo: La función f(x)
= x 5 , x ∈ lR es impar pues ∀ x ∈ Dom(f) = lR se tiene
2
 además
x + 3 f(; -x) =x(-x)
≥ 05 = - ( x )5 = - f(x)
(x) ∈ Dom(f)
Ejemplo:
f(x) =
= lR

 x + 4 −1 ; − 4 ≤ x < 0
7)
Funciones Monótonas:
Inmediatamente
f1 (x) = x2 +3Estrictamente
es inyectiva encreciente
[0, +∞⟩ , y decreciente.
i) Una función f es estrictamente creciente en I ⊂ Dom(f) si:
∀ x1 , x2 ∈ I con x 1 < x2 entonces f(x 1 ) < f(x2 ).
- 30 - en I ⊂ Dom(f) sí:
ii) Una función f es estrictamente decreciente
∀ x1 , x2 ∈ I con x 1 < x2 entonces f(x 1 ) > f(x2 ).
Ejemplo: f(x) = x 2
La función es creciente en I1 = [ 0, ∞ ⟩ pues si x i ≥ 0 ∀ xi ∈ I y x 1 < x 2
entonces (x 1 )2 < (x2 )2 entonces f(x 1 ) < f(x2 )
La función es decreciente en I2 = ⟨ - ∞ , 0 ⟩ pues si xi < 0 ∀ x i ∈ I2 y x 3 < x4
entonces –x 3 > -x4 ≥ 0 entonces (-x4 )2 < (-x3 )2 entonces (x4 )2 < (x3 )2 entonces f(x 4 ) < f(x3 )
8) Funciones Inyectiva, Sobreyectiva, Biyectiva:
i) Una función f: A → B es inyectiva
⇔ ∀ x1 , x2 ∈ Dom(f) con f(x1 ) = f (x 2 ) ⇒ x 1 = x 2
⇔ ∀ x1 , x 2 ∈ Dom(f) y x1 ≠ x2 ⇒ f(x1 ) ≠ f(x2 )
ii) Una función f : A → B es sobreyectiva
⇔ ∀ y ∈ B ∃ x ∈ Dom(f) tal que y = f(x) ⇔ Ran(f) = B.
Funciones en una variable R eal
f2 (x) =
CÁLCULO DIFERENCIAL E INTEGRAL I
x + 4 -1 es inyectiva en [ -4, 0⟩
Además si x ≥ 0 ⇒ x ≥ 0 ⇒ f1 (x) = x2 +3 ≥ 3
Si –4 ≤ x < 0 ⇒ 0 ≤ x+4 < 4 ⇒ 0 ≤ x + 4 < 2 ⇒ -1 ≤ x + 4 -1 < 1 ⇒ -1 ≤ f2 (x) < 1
Por tanto Ran(f1 )∩Ran(f2 ) = Φ entonces f será inyectiva.
2
2.4. OPERACIONES CON FUNCIONES, FUNCIÓN COMPUESTA E INVERSA.
Definición2.4. (Suma resta , producto y cociente de funciones )
Dadas las funciones f, g : A → B definimos:
1) f ± g : A → B tal que (f ± g)(x) = f(x) ± g(x) ,
Dom(f ± g) = Dom(f) ∩ Dom(g)
2) f .g : A → B tal que (f.g)(x) = f(x).g(x) ,
Dom(f.g) = Dom(f) ∩ Dom(g)
3)
f
g
f
f (x)
g
g ( x)
: A → B tal que ( )( x ) =
Dom(
f
g
, g ≠0
) = ( Dom(f) ∩ Dom(g) ) - {x ∈A tal que g(x) = 0}
Ejemplo: Dada f(x) = | x |-[[x]] hallar dominio rango graficar.
Considerando g(x) = | x |, h(x) = [[x]] entonces f(x) = g(x)-h(x).
De allí que Dom(f) = Dom(g) ∩ Dom(h) = lR
Para determinar el rango en estos tipos de ejemplos se sugiere primeramente dividir el dominio
de f en intervalos con una sola correspondencia alrededor de cero, determinar el rango de f en
estos intervalos y con ello deducir el rango total de f.
Si x∈[- 2, - 1⟩ ⇒ f(x) = -x+2 ∈⟨ 3, 4]
y
Si x∈[-1, 0⟩ ⇒ f(x) = -x+1 ∈⟨ 1, 2]
•
Si x∈[0, 1⟩ ⇒ f(x) = x ∈[0, 1⟩
3
Si x∈[1, 2⟩ ⇒ f(x) = x -1 ∈[0, 1⟩
Ahora sea: n∈Z + entonces:
Si x∈[-n, -n+1⟩ ⇒ f(x) = -x+n∈⟨ 2n-1, 2n]
Si x∈[n, n+1⟩ ⇒ f(x) = x -n∈[0, 1⟩
Por tanto: Ran(f) = [0, 1⟩ ∪ U ⟨ 2n − 1, 2n]
2
•
1
n∈Z +
-2
-1
•
•
1
2
x
Definición 2.5. (Función compuesta)
Sean f : A → B y g : B → C dos funciones tales que Rang(f) ∩ Dom(g) ≠ φ la función
composición de f con g es dada por go f : A → C / (go f)(x) = g(f(x)).
Dom(go f) = { x ∈ Dom(f) / f(x) ∈ Dom(g) }
Ejemplo: Dadas las funciones f(x) =
x , g(x) = x 2 – 1.
Dom(f) = [ 0, ∞ ⟩ , Dom(g) = lR
Ran(f) = [ 0, ∞ ⟩ , Ran(g) = [- 1, ∞ ⟩ ⇒ Ran(g) ∩ Dom.(f) = [ 0, +∞⟩ ≠ φ
Por definición : (fo g)(x) = f(g(x)) = f(x 2 –1) =
- 31 -
x2 −1
Dom(f) = Rang(f ) ,
Dom(f -1 ) = Ran(f)
Veamos: Dom(f) = Ran(f -1 )
Funciones en una variable R eal
CÁLCULO DIFERENCIAL E INTEGRAL I
i) Sea x ∈Dom(f) ⇒ f(x) = y ∈Ran(f) ⇒ f-1 (y) = f-1 (f(x)) = x ∈Ran(f-1 )
entonces Dom(f) ⊆ Ran(f -1 )
Dom(fo g) = { x∈Dom(g) / g(x) ∈ Dom(f) } = { x ∈lR / x2 -1 ∈[0, ∞ ⟩ }
= { x ∈lR / x 2 -1 ≥ 0 } = { x ∈lR / x ∈⟨ - ∞ ,- 1] ∪ [1, ∞ ⟩ }
ii) Sea x ∈ Ran(f-1 ) ⇒ ∃y∈Dom(f-1 ) tal que f-1 (y) = x , y = f(x 1 ), x1 ∈Dom(f) ⇒ f-1 (f(x1 )) =
= ⟨ - ∞ ,- 1] ∪ [1, ∞ ⟩
x1 = x , y = f(x) ⇒ x∈Dom(f) entonces Ran(f -1 ) ⊆ Dom(f)
De (i) y (ii) se tiene Dom(f) = Ran(f -1 ).
Observación: La composición de funciones es asociativa (fo g)o h = fo (go h)
Peroseno
es conmutativa
o g ≠ go f
Análogamente
tiene:
Dom(f -1 ) = fRan(f)
Definición
2.6. (Función Inversa)
De la observación anterior(4):
Diremos que una función f : (a,
A → B tiene inversa si existe una función-1 g : B → A tal que
b) ∈Gráfico de f ⇔ (b, a) ∈Gráfico de f.
fo g = 1B , go f = 1 A. La función g es llamada la función inversa de f .
Notación g = f -1
O sea las gráficas de f y f -1 son simétricas respecto de la recta y = x
Teorema 2.1. Una función f : A → Ran(f) es inyectiva ⇔ tiene inversa.
Demostración:
( ⇒ ) Si f es inyectiva ∀ b ∈ Ran(f) ∃ a(único) / f(a) = b definimos g : B → A / g(b) = a
y f(a) = b ∈ Ran(f) por unicidad de a la- función
g está bien definida
32 Así g(f(a)) = g(b) = a = 1 A(a) y f(g(b)) = f(a) = b = 1 A(b) entonces go f = 1 A y fo g = 1B
( ⇐ ) Sí f tiene inversa ∃ g : B → A tal que go f = 1 A ó sea g(f(x)) = x
Sí f(a1 ) = f(a2 ) ⇒ g(f(a1 )) = g(f(a2 )) ⇒ a1 = a2
Observaciones:
1) f : A → B es biyectiva ⇔ tiene inversa
2) De la proposición anterior. Si f no es inyectiva ⇒ no tiene inversa.
3) Si f, g son invertibles entonces fo g es invertible y (fo g)-1 = g-1 o f-1
4) Como f -1 o f = 1A y fo f -1 =1B entonces:
Dom(f) = Rang(f -1 ) ,
Funciones en una variable R eal
Ejemplo : Considerar
CÁLCULO DIFERENCIAL E INTEGRAL I
f(x) = 5x+3. Averiguar la inversa.
Como f es biyectiva tiene inversa. Además f(f -1 (y)) = y
y −3
Entonces f(f -1 (y)) = 5(f -1 (y)) + 3 = y ⇒ f −1 ( y ) =
⇒ f
5
−1
(x) =
x−3
5
Teorema 2.2. Sean f : A → B , g : B → C dos funciones entonces:
i) Si f, g son inyectivas entonces go f es inyectiva.
ii) Si f, g son sobreyectivas entonces go f es sobreyectiva.
iii) Si go f es inyectiva entonces f es inyectiva
iv) Si go f es sobreyectiva entonces g es sobreyectiva
Demostración:
i) Si x 1 ∈Dom(go f), (go f)(x1 ) = (go f)(x2 ) ⇒ f(x1 ) = f(x 2 ) pues g es inyectiva
⇒ x1 = x2 pues f es inyectiva .
ii) Sea c ∈C ⇒ ∃b∈B tal que g(b) = c pues g es sobreyectiva.
⇒ ∃a∈A tal que f(a) = b pues f es sobreyectiva.
⇒ ∃a ∈A tal que g(f(a)) = g(b) = c ⇒ go f sobreyectiva
iii) Sea f(x 1 ) = f(x2 ) ⇒ go (f(x1 )) = go (f(x2 )) ⇒(go f)(x 1 ) = (go f)(x 2 )
⇒ x1 = x2 pues go f es inyectiva ⇒ f es inyectiva.
iv) Sea c ∈C ⇒ ∃a∈A tal que g(f(a)) = c pues go f es sobreyectiva.
⇒ ∃f(a) = b ∈B tal que g(b) = c ⇒ g es sobreyectiva.
Ejemplo Dada la función h(x) = −
x 2 + 6 x − 7 ; x ≤ -7. Determinar h -1 (x) si existe.
Consideremos f(x) = x 2 +6x-7 , g(x) = -
x . Como f, g son inyectivas ∀ x ≤ - 7
- 33 -
Funciones en una variable R eal
CÁLCULO DIFERENCIAL E INTEGRAL I
Por el teorema anterior h(x) = (go f)(x) es inyectiva.
Entonces ∃h-1 además h(h-1 (x)) = x ⇔ x = −
(h −1 ( x )) 2 + 6(h −1 ( x )) − 7
⇒ h-1 (x) = -3 ± 16 − x 2 tal que Dom(h) = ⟨ -∞, -7]
⇒ Ran(h-1 ) = ⟨ -∞, -7] ,
16 − x 2 ≥ 4
⇒ h-1 (x) = -3 − 16 − x 2 ; x ≤ 0
2.5. FUNCIONES TRIGONOMETRICAS Y SUS INVERSAS.
Recordemos previamente el Círculo Trigonométrico Unita io:
Sabemos:
sen(x) = b , cos(x) = a ,
b
a
tg(x) =
; a ≠ 0 , ctg(x) =
; b≠0 ,
a
b
1
1
sec(x) =
; a ≠ 0 , csc(x) =
; b≠0
a
b
También: 180o = πRad
Sistemas angulares de valores que puede tomar x.
Claramente cada ángulo x puede ser considerado
como un número real.
Funciones trigonométricas ó elementales :
1) Función Seno: f : lR → lR / f(x) = sen(x)
Del círculo Unitario Dom(f) = lR , Ran(f) = [-1, 1]
La función seno es periódica de periodo fundamental T = 2 π
En efecto supongamos sen(x+T) = sen(x) ⇒ sen(x)cos(T)+cos(x)sen(T) = sen(x)
Si x = π/2 ⇒ cos(T) = 1, también cos2 (T)+sen2 (T) = 1 ⇒ cos(T) = 1 ∧ sen(T) = 0
entonces el menor valor T > 0 sería T = 2 π
La función seno es impar pues sen(-x) = -sen(x).
O sea simétrica respecto del Origen tabulando:
x
Sen(x)
0+kπ
0
π/2 +2k π
1
Por periodicidad
Gráfico:
- 34 -
(3 π)/2 +2k π
-1
por periodicidad
Funciones en una variable R eal
CÁLCULO DIFERENCIAL E INTEGRAL I
2) Función Coseno: f : lR → lR / f(x) = cos(x)
Del Circulo Unitario: Dom(f) = lR , Ran(f) = [-1,1]
La función coseno es periódica de periodo fundamental T = 2π
La función coseno es par pues cos(-x) ) = cos(x). O sea simétrica respecto del eje Y
Tabulando:
x
π/2+kπ
2k π
π +2k π
cos(x)
0
1
-1
por periodicidad
Por periodicidad
Gráfico:
sen x
cos x
Dom(f) = { x ∈ lR / cos(x) ≠ 0 }= lR - { π/2 +k π : k ∈Z }. Ran(f) = lR
La función tangente es periódica de periódo fundamental T = π
La función tangente es impar ó sea simétrica respecto del Origen.
3) Función Tangente: f : lR → lR / f(x) = tg(x) =
El gráfico tiene asíntotas para cos(x) = 0 ⇔ L : x = π/2 +k , k∈Z
Gráfico:
cos x
sen x
Dom(f) = { x ∈ lR / sen(x) ≠ 0 } = lR - { k π : k ∈Z }. Ran(f) = lR
La función cotangente es periódica de periodo fundamental T = π
La función es impar ó sea simétrica respecto del Origen.
4) Función Cotangente: f : lR → lR / f(x) = ctg(x) =
El gráfico tiene asíntotas para sen(x) = 0 ⇔ L : x = kπ , k ∈Z .
Grafico
- 35 -
Funciones en una variable R eal
CÁLCULO DIFERENCIAL E INTEGRAL I
1
cos x
Dom(f) = {x ∈ lR / cos(x) ≠ 0 } = lR -{ π/2+k π : k ∈Z }. Ran(f) = ⟨ -∞ , - 1] ∪ [1, ∞ ⟩
La función secante es periódica de periódo fundamental T = 2π
La función secante es par ó sea simétrica respecto del eje Y.
5) Función Secante: f : lR → lR / f(x) = sec(x) =
El gráfico tiene asíntotas para cos(x) = 0 ⇔ L : x = π/2+k , k ∈Z
Gráfico
1
sen x
Dom(f) = { x ∈ lR / sen(x) ≠ 0 } = lR - { k π : k ∈Z }. Ran(f) = ⟨ -∞ , -1] ∪ [1, ∞ ⟩
La función cosecante es periódica de periodo fundamental T = 2 π
La función cosecante es impar ó sea simétrica respecto del origen.
6) La función Cosecante: f : lR → lR / f(x) = csc(x) =
E l gráfico tiene asíntotas para sen(x) = 0 ⇔ L : x = k π , k ∈Z
Funciones trigonométricas inversas :
Considerando las siguientes restricciones de las funciones trigonométricas elementales
f(x) = sen(x) : x ∈[- π/2, π/2 ] es inyectiva luego tiene inversa.
f(x) = cos(x) : x ∈[0, π ] es inyectiva luego tiene inversa.
f(x) = tang(x) : x ∈⟨ - π/2, π/2 ⟩ es inyectiva luego tiene inversa.
f(x) = ctg(x) : x ∈⟨ 0, π ⟩ es inyectiva luego tiene inversa.
f(x) = sec(x) : x ∈[0, π/2 ⟩ ∪ ⟨ π/2, π ] es inyectiva luego tiene inversa.
f(x) = csc(x) : x ∈[- π/2, 0⟩ ∪ ⟨ 0, π/2 ] es inyectiva luego tiene inversa.
1) Función inversa del seno g : lR → lR / g(x) = arcsen(x) : x ∈[ -1, 1]
Dom(g) = [ -1, 1] , Ran(g) = [ -π/2, π/2]
- 36 -
Funciones en una variable R eal
CÁLCULO DIFERENCIAL E INTEGRAL I
Gráfico:
2) Función inversa del coseno g : lR → lR / g(x) = arccos(x) : x ∈[ -1, 1]
Dom(g) = [ -1, 1] ,
Ran(g) = [0, π ]
Gráfico:
3) Función inversa de la tangente g : lR → lR / g(x) = arctg(x) : x ∈lR
Dom(g) = lR ,
Ran(g) = ⟨ -π/2, π/2⟩
Gráfico:
4) Función inversa de la cotangente g : lR → lR / g(x) = arcctg(x) : x ∈lR
Dom(g) = lR ,
Ran(g) = ⟨ 0, π ]
Gráfico:
- 37 -
Funciones en una variable R eal
CÁLCULO DIFERENCIAL E INTEGRAL I
5) Función inversa de la secante g : lR → lR / g(x) = arcsec(x) : x ∈ ⟨ - ∞ ,- 1] ∪ [1, ∞ ⟩
Dom(g) = ⟨ - ∞ , -1] ∪ [1, ∞ ⟩ ,
Ran(g) = [ 0, π/2 ⟩ ∪ ⟨ π/2, π]
Gráfico:
6) Función inversa de la cosecante g : lR → lR / g(x) = arccsc(x) : x ∈ ⟨ -∞ , - 1] ∪ [1, ∞ ⟩
Dom(g) = ⟨ - ∞ , -1] ∪ [1, ∞ ⟩ ,
Ran(g) = [- π/2, 0 ⟩ ∪ ⟨ 0, π/2 ]
Gráfico:
2.6. FUNCIONES EXPONENCIALES, HIPERBÓLICAS Y LOGARÍTMICAS.
1) Función Exponencial f : lR → lR / f(x) = a x , a ≠ 1 , a ∈ lR +
Primer caso: Si 0 < a < 1 .
Dom(f) = lR , Para determinar el Rango podemos tener en cuenta lo siguiente:
Sí x = 0 ⇒ f(0) = a 0 = 1
Sí x se aproxima a - ∞ ⇒ f(x) = a x se aproxima a ∞
Sí x se aproxima a ∞ ⇒ f(x) = a x se aproxima a 0
Entonces la función es decreciente y Ran(f) = ⟨ 0, ∞ ⟩
Gráfico:
- 38 -
Funciones en una variable R eal
CÁLCULO DIFERENCIAL E INTEGRAL I
Segundo caso: Si a > 1
Dom(f) = lR , Para determinar el Rango podemos tener en cuenta lo siguiente:
Sí x = 0 ⇒ f(0) = a 0 = 1
Si x se aproxima a - ∞ ⇒ f(x) = a x se aproxima a 0
Si x se aproxima a ∞ ⇒ f(x) = a x se aproxima a ∞
Entonces la función es creciente y Rang(f) = ⟨ 0, ∞ ⟩
Gráfico:
Observación:
x
Particularmente se tiene las funciones f(x) = e , g(x) = e
-x
donde e = Número de Euler.
2) Funciónes hiperbólicas
De la observación anterior obtenemos las llamadas funciones hiperbólicas .
e x − e −x
Seno hiperbólico: y = f(x) = senh(x) =
2
e x + e −x
Coseno hiperbólico: y = f(x) = cosh(x) =
2
senh( x )
Tangente hiperbólica: y = f(x) = tgh(x) =
cosh(x)
cosh(x)
Cotangente hiperbólica: y = f(x) = ctgh(x) =
senh( x )
1
Secante hiperbólica: y = f(x) = sech(x) =
cosh(x)
1
Cosecante hiperbólica: y = f(x) = csch(x) =
senh( x )
3) Función Logaritmo f : lR → lR / f(x) = Log a x ; a ≠ 1, a∈lR+
Primer caso: Si 0 < a < 1
Dom(f) = ⟨ 0, ∞ ⟩ , Para determinar e l Rango podemos tener en cuenta lo siguiente:
Si x = 1 ⇒ f(x) = Log a 1 = 0
Sí x se aproxima a 0 ⇒ f(x) = Loga x se aproxima a ∞
Sí x se aproxima a ∞ ⇒ f(x) = Log a x se aproxima a - ∞
Entonces la función es decreciente y Ran(f) = lR
- 39 -
Observaciones:
1) Sí f(x)en=una
ax variable
, g(x) =R Log
Funciones
eal a x
entonces:
CÁLCULO DIFERENCIAL E INTEGRAL I
(log x )
(fo g)(x) = f(g(x)) = f(Loga x) = a a = x = 1d (x)
(go f)(x) = g(f(x)) = g(ax ) = Loga a x = x = 1d (x)
Gráfico:
Por lo tanto las funciones logaritmo
y y exponencial son inversas una de otra.
2) Usando propiedades de biyectividad y Log
crecimiento,
podemos solucionar las
<1
a (x) ; 0 < a decrecimiento
siguientes ecuaciones e inecuaciones con exponenciales y logaritmos en una misma base.
i) Sí a > 1
( ab = ac ⇔ b = c )
y
( Log a b = Log a c ⇔ b = c )
b
c
0
1
x ac ⇔ b<c)
(a <a ⇔ b<c)
y
( Log a b < Log
b
c
(a >a ⇔ b>c)
y
( Log a b > Log a c ⇔ b > c )
ii) Sí 0 < a < 1
( a b = ac ⇔ b = c )
y
( Log a b = Log a c ⇔ b = c )
Segundo caso: Sí ab > 1c
(a <a ⇔ b>c)
y
( Log a b < Log a c ⇔ b > c )
Dom(f) = ⟨ 0, ∞ ⟩( ,a bPara
> ac determinar
⇔ b < c )el Rango
y podemos
( Log a b tener
> Logena ccuenta
⇔ blo< siguiente:
c)
Sí x = 1 ⇒ f(x) = Log a 1 = 0
Sí x se aproxima a 0 ⇒ f(x) = Log a x se aproxima a - ∞
- 40
Sí x se aproxima a ∞ ⇒ f(x) = Log a x se
aproxima
a ∞
Entonces es creciente y Ran(f) = lR
Gráfico:
y
Log a(x) ; a > 1
0
1
x
Funciones en una variable R eal
CÁLCULO DIFERENCIAL E INTEGRAL I
3) En exponenciales y logaritmos también se tiene:
i) ax+ y = a x.ay
ii) Loga (xy) = Loga x + Loga y
iii) Log a (x/y) = Log a x - Log a y
iv) Si r ∈lR ⇒ rLoga x = Log a xr
4) Particularmente sí a = e (Número de Neper). Denotaremos Loge x = Ln x
De allí si y = Log a x ⇒ ay = x por( 1) ⇒ Ln ay = Ln x ⇒ yLn a = Ln x
⇒ y=
ln x
ln x
. Por lo tanto Loga x =
ln a
ln a
4z + 7
< 1 se quiere el conjunto solución.
8 − 5z
4z + 7
ln z
Primeramente sabemos: log z
<1 =
= log z z
8 − 5z
ln z
Por contenido teórico debemos tener que:
4z + 7
4z + 7
4z + 7
>0 ∧ [(0<z<1 ∧
>z ) ∨ (z>1 ∧
< z )]
8 − 5z
8 − 5z
8 − 5z
4z + 7
7 8
7 8
i)
> 0 ⇔ z ∈ ⟨ − , ⟩ ⇒ C.S. 1 = ⟨ − , ⟩
8 − 5z
4 5
4 5
Ejemplo : Dada la inecuación log z
ii)
0 < z < 1 ∧ (4z+7) > z(8- 5z)
⇒ C.S.2 = ⟨ 0, 1⟩
iii)
8
> z >1 ∧ (4z+7) < z(8 -5z)
5
⇒ C.S.3 = Φ
iv) z ≥
8
∧ (4z+7) > z(8 -5z)
5
⇒ C.S.4 = [
8
,∞⟩
5
iv) C.S.2 ∪ C.S.3 ∪ C.S.4 = C.S.5 = ⟨ 0, 1⟩ ∪ ⟨
8
,∞⟩
5
Por lo tanto C.S. = C.S.1 ∩ C.S.5 = ⟨ 0, 1⟩
Ejercicio: Resolver
Solución:
3
2
4 x ( x +1) 2 − 2 x + x > 2
3
2
4 x ( x +1) 2 − 2 x + x > 2
⇔
⇔
3
3
4 2 x +2 x 2 − 2 x + x > 2
2
3x
2
>2
1
2
⇔
1
⇒ C. S. = ⟨ , + ∞⟩
3
- 41 -
3x 1
>
2 2
Funciones en una variable R eal
CÁLCULO DIFERENCIAL E INTEGRAL I
5) Funciones Hiperbólicas inversas
e x − e −x
Dado el seno hiperbólico y = f(x) = senh(x) =
2
Si x1≠x2 ⇒ e
2 x1
−1 ≠ e
2 x2
− 1 ⇒ e (e
x2
2 x1
− 1) ≠ e (e
x1
2 x2
e x − e − x e x − e −x
− 1) ⇒
≠
2
2
1
1
2
2
Por tanto la función seno hiperbólico es inyectiva.
Análogamente todas las funciones hiperbólicas son inyectivas en su dominio y por lo tanto
tienen inversa:
i)
Inversa del seno hiperbólico: y = f(x) = senh -1 (x)
Dom(f) = lR,
Ran(f) = lR
e y − e −y
Si y = senh-1 (x), x∈lR ⇒ x = senh(y) =
, y∈lR
2
( ) − 1 ⇒ (e
⇒ 2 xe y = e y
⇒ ey =
2x ±
⇒ e =x+
y
⇒ y = ln( x +
2
y
) 2 − 2 xe y − 1 = 0
( −2 x ) 2 + 4
2
x +1 > 0
2
x 2 + 1) , x∈lR
Por lo tanto y = senh -1 (x) = ln( x +
x 2 + 1) , x∈lR
ii) Inversa del coseno hiperbólico: y = f(x) = cosh -1 (x)
Dom(f) = [1, +∞ ⟩ ,
Ran(f) = lR
Análogamente y = cosh-1 (x) = ln( x +
x 2 − 1) , x ≥ 1.
iii) Inversa de la tangente hiperbólica: y = f(x) = tgh -1 (x)
Dom(f) = ⟨ -1, 1⟩ ,
Ran(f) = lR
e y − e −y
-1
Si y = tgh (x), | x | <1 ⇒ x = tgh(y) = y
e + e −y
x +1
 x + 1
⇒ e 2y =
⇒ 2 y = ln 

x −1
 x −1
1  x +1
Por lo tanto y = tgh -1 (x) = ln 
 , | x | <1
2  x −1
iv)
Inversa de la cotangente hiperbólica: y = f(x) = ctgh -1 (x)
Dom(f) = ⟨ +∞, - 1⟩ ∪ ⟨ 1, +∞⟩ ,
Ran(f) = lR -{0}
1  x +1
Análogamente y = ctgh -1 (x) = ln 
 , | x | >1
2  x −1
- 42 -
Funciones en una variable R eal
v)
CÁLCULO DIFERENCIAL E INTEGRAL I
Inversa de la secante hiperbólica: y = f(x) = sech -1 (x)
Dom(f) = ⟨ 0, 1] ,
Ran(f) = lR
2
Si y = sech-1 (x), x∈lR ⇒ x = sech(y) = y
e − e −y
⇒ x (e y ) 2 − 2e y + x = 0
⇒ e =
y
⇒ e =
y
1 ± 1− x2
x
1 + 1− x 2
1+
⇒ y = ln 


x
>0
1 − x 2 

x

1+
Por lo tanto y = sech (x) = ln 


-1
vi)
1 − x 2 
, x∈⟨ 0, 1]

x

Inversa de la cosecante hiperbólica: y = f(x) = csch -1 (x)
Dom(f) = lR -{0},
Dom(f) = lR -{0}
1+ 1 + x2
Análogamente y = csch-1 (x) = ln 

x

- 43 -

,x≠0


Funciones en una variable R eal
CÁLCULO DIFERENCIAL E INTEGRAL I
2.7. RELACIÓN DE EJERCICIOS.
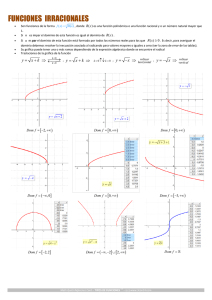
I.
Dadas las relaciones hallar Dominio, Rango y aproximar grafico.
x 2 − 3x + 2
ℜ1 = { (x, y) ∈lR2 / y = − 4 − x 2 } ; ℜ6 = { (x, y) ∈lR2 / y =
}
x2 −4
II. Dadas las funciones hallar Dominio, Rango y Graficar:
x .( x 4 − 13 x 2 + 36 )
1) f(x) = 3
2) f(x) = | x | + | x – 1 |
x + 2 x 2 − 9 x − 18
 4 − x2 ; x ≤1
4) f(x) = 
2
 2+ x ; x ≥ 2
3) f(x) = x – x
III. 1.- Dada la función f probar:
f ( x) + f (− x )
es par,
f ( x) − f (− x )
2
2
2 .- Hallar los intervalos en que la función es Creciente y Decreciente:
es impar
f(x) = x, f(x) = x 2 + 1, f(x) = (x -2)2 + 2, f(x) = | x 2 – 4 |, f(x) = (x – 1)3
IV. 1. - Dadas f(x) = x 2 – 3, g(x) = x 3 + 4x2 + 1 Hallar (f+g)(x), (f-g)(x), (f.g)(x)
2. - Dadas a) f(x) = x 2 –3, g(x) = x 3 + 4x2 +1 b) f(x) =
Hallar f o g, g o f, f o f y sus dominios
x , g(x) = x 2 – 1
3. - Dadas las funciones determinar f o g y su Dominio
f(x) =
x +1
x−4
,
 | 1 − x | −2 ; x > 3
g(x) = 
2
 [[ x − 1]] ; 0 ≤ x ≤ 3
V. Verificar sí las siguientes funciones son biyectivas y hallar la inversa:
x +1
2x + 3
ex − e−x
f(x) =
, f(x) =
, f(x) = 2| x | + x, f(x) = x 3 , f(x) =
x −1
x −1
2
x
x −2
f : lR → ⟨ -1, 1 ⟩ / f(x) =
, f(x) =
1+ | x |
x+2
VI. 1) Sí x ∈ [ -2 π, 2 π ] graficar: f(x) = sen( π[[x]]), f(x) = 2 | sen| x | |, f(x) = sen| 2x |
p [[ x ]]
px
x
p
f(x) = cos(
), f(x) = 2cos(
), f(x) = tg + sen x , f(x) = sen(x - )
2
2
2
4
- 2x
2) Graficar: f(x) = e , f(x) = ln(2x), f(x) = 2 | arcsen x |
- 44 -