Jacobo Bermúdez Fernández María Casanova Vázquez

P GP
Jacobo Bermúdez Fernández
María Casanova Vázquez
PGP
ÍNDICE
1. Introducción a PGP…………………………………………………………………..4
1.1 Descripción………………………………………………………………….4
1.2 Motivaciones………………………………………………………………...5
1.3 Servicios que ofrece…………………………………………………………5
2. Historia de PGP………………………………………………………………………6
2.1Precedentes de PGP………………………………………………………….6
2.2 Nacimiento y evolución de PGP…………………………………………….6
3. Software:
3.1 Obtención e instalación…………………………………………………….10
3.2 Proyectos open source……………………………………………………...11
4. Principios básicos de PGP…………………………………………………………...12
4.1Sistemas de cifrado y caso concreto de PGP………………………………..12
4.1.1. Sistema de cifrado simétrico (o de clave secreta)………………..12
4.1.2. Sistema de cifrado asimétrico (o de clave pública)………………13
4.1.3. Sistema de cifrado híbrido (el que usa PGP)…………………….14
4.2 Algoritmos de cifrado………………………………………………………16
4.2.1. Algoritmos de cifrado asimétrico………………………………...16
4.2.2. Algoritmos de cifrado simétrico…………………………………20
4.2.3. Algoritmos de hash o de resumen………………………………..25
4.3 Firma digital………………………………………………………………...29
4.4 Certificados digitales……………………………………………………….31
4.4.1. Distribución de certificados……………………………………...32
4.4.2. Formatos de certificados…………………………………………32
4.4.3. Validez y confianza……………………………………………...34
4.4.4. Modelos de confianza…………………………………………....34
4.4.5. Niveles de confianza en PGP……………………………………36
4.4.6. Revocación desertificados……………………………………….36
4.5. Anillo de claves……………………………………………………………37
5. Modo de funcionamiento……………………………………………………………39
5.1 Creación y manejo de las claves…………………………………………...39
5.2 Exportación e importación de claves públicas. Servidores de claves……...42
5.3 Funcionamiento general…………………………………………………...44
5.3.1. Envío de mensajes……………………………………………….44
5.3.2. Recepción de mensajes………………………………………….48
6. Ejemplo de uso de un software concreto……………………………………………50
7. Problemas y vulnerabilidades de PGP………………………………………………55
8. Otras aplicaciones de PGP…………………………………………………………..58
8.1 Cifrado para asegurar tus propios documentos…………………………….58
8.2 Uso de PGP para borrar archivos del disco ………………………………..59
-2-
PGP
9. S/MIME, PGP/MIME……………………………………………………………….60
9.1. S/MIME……………………………………………………………………60
9.2. PGP/MIME………………………………………………………………...60
10. Referencias…………………………………………………………………………61
11. Índice de figuras y tablas…………………………………………………………...63
-3-
PGP
1. INTRODUCCIÓN A PGP
1.1. Descripción
PGP, Pretty Good Privacy (“Privacidad bastante buena”), creado en 1991 por
Philip Zimmermann, es una aplicación informática de criptografía de alta seguridad.
PGP permite intercambiar ficheros y mensajes con confidencialidad, autenticación,
integridad. Confidencialidad quiere decir que sólo podrán leer el mensaje aquellos a
quienes va dirigido. Autenticación quiere decir que los mensajes que parecen ser de
alguien sólo pueden venir de esa persona en particular. Integridad quiere decir que el
mensaje no es modificado por terceras personas y llega al receptor tal cual se había
enviado.
No se necesitan canales seguros para intercambiar claves entre usuarios, por lo
que PGP resulta mucho más fácil de utilizar. Esto se debe a que PGP está basado en la
tecnología llamada criptografía de clave pública. En un sistema de clave pública, cada
usuario crea un par de claves que consiste en una clave pública y una clave privada. Se
puede cifrar un mensaje con la clave pública y descifrarlo con la privada y viceversa
(NO se puede cifrar y descifrar con la misma clave). El usuario difunde la clave pública,
poniéndola a disposición de cualquiera que quiera enviarle un mensaje. Una vez que el
mensaje ha sido recibido por el usuario, éste podrá descifrarlo con su clave privada. Es
evidente que la clave privada debe ser mantenida en secreto por el propietario. PGP
también se basa en criptografía de clave privada, de hecho combina ambos como
veremos más adelante.
PGP también permite al receptor verificar que los mensajes provienen realmente
de quien dice ser el emisor y no han sido alterados, ya sea accidentalmente o
maliciosamente. Esto es posible gracias a que permite firmar digitalmente los
documentos. PGP firma el mensaje usando la clave privada del emisor del mensaje, de
tal forma que el receptor puede comprobar su autenticidad con la clave pública del
emisor. De esta forma nadie que no conozca tú clave privada puede firmar por ti.
La preocupación creciente por la seguridad en el correo electrónico ha llevado
en los últimos años a la aparición de sistemas más o menos fiables y más o menos
cómodos de utilizar. Aunque todavía no se adoptado ninguno de ellos como estándar
aceptado por todo el mundo, cada vez se afianza mas la utilización de PGP como medio
para garantizar la confidencialidad, autentificación e integridad en el correo electrónico.
PGP es una aplicación de propósito general independiente del Sistema
Operativo. Las claves de su éxito son:
•
•
•
Software de dominio público.
PGP corre en una gran variedad de plataformas.
Está basado en algoritmos extremadamente seguros.
Resumiendo, los cuatro usos básicos de PGP son:
•
Cifrar un mensaje o fichero de tal forma que sólo un receptor pueda
descifrarlo y leerlo, aquel al que está dirigido.
-4-
PGP
•
•
•
Firmar un mensaje de tal forma que el receptor sepa que viene del emisor y
no de un impostor.
Cifrar ficheros de tal forma que sólo los pueda descifrar el que los cifró.
Borrar realmente ficheros.
1.2. Motivaciones
En un artículo escrito por Philip Zimmermann en la primera edición de la guía
del usuario en 1994 cuenta las motivaciones que lo llevaron a crear PGP. En este
artículo defiende el derecho constitucional de la intimidad y los problemas que ponía el
gobierno de Estados Unidos en aquella época para conseguirla. Según Philip el simple
hecho de querer tener privacidad en nuestro correo electrónico supone ser sospechosos
de estar haciendo algo ilegal. Lo que él propone es que el uso de algún sistema de
cifrado de mensajes sea algo extendido entre los usuarios de correo electrónico para que
se convierta en algo tan normal como mandar las cartas en sobres y no en postales.
El motivo de usar PGP es simplemente obtener privacidad en nuestras
comunicaciones vía e-mail, pues a nadie le gusta que lean su correo, a pesar de que los
temas tratados no sean confidenciales o ilegales. El correo electrónico es actualmente
menos seguro que el correo ordinario pues es habitual que un mensaje enviado a través
de Internet pase por varias estafetas y un postmaster o cualquier usuario con privilegios
puede acceder a estos mensajes, leerlos y/o alterarlos. Además de esto no es difícil
falsificar las direcciones del emisor de un mensaje. Por eso en caso de que se desee
obtener seguridad en el correo electrónico a través de Internet es necesario usar algún
medio que nos proporcione garantías suficientes de confidencialidad, autentificación e
integridad.
1.3. Servicios que ofrece
•
•
•
•
Confidencialidad: garantiza, mediante técnicas de cifrado, que sólo el
destinatario podrá descifrar y leer el mensaje.
Integridad: impide cualquier tipo de manipulación sobre el contenido de
mensaje por parte de terceras personas, asegurando así que el mensaje es
recibido tal como fue emitido.
Autenticación: permite a un usuario firmar un documento antes de enviarlo,
de forma que no quede duda al destinatario sobre la procedencia de dicho
mensaje y sobre la identidad del remitente.
No repudio: va ligado al servicio de autenticación. Si firmamos un
documento, además de garantizar al receptor que lo hemos enviado nosotros,
después no podemos negar el hecho, pues nadie salvo nosotros puede firmar
con nuestra clave privada.
-5-
PGP
2. HISTORIA DE PGP
2.1. Precedentes de PGP.
La criptografía es una antigua ciencia y a la vez que los ordenadores se han
hecho más y más potentes el número de gente trabajando en este tema ha crecido en
gran medida. La preocupación de los gobiernos sobre la expansión de las técnicas de
cifrado ha aumentado en los últimos años, aunque la codificación es de uso totalmente
legítimo por parte de los ciudadanos, puede ser una potente herramienta para los
criminales.
En 1976 el criptógrafo y abogado Whitfield Diffie, junto con un ingeniero
eléctrico llamado Martin Hellman descubre la criptografía de clave pública. De sus
iniciales viene el nombre del algoritmo de creación de claves D-H = Diffie-Hellman.
En 1977 Ron Rivest, Adi Shamir, y Len Adleman descubren otro sistema más
general de clave pública llamado RSA (por los apellidos Rivest, Shamir, and Adleman)
Los tres eran investigadores del MIT. La NSA (Agencia Nacional para la Seguridad en
Estados Unidos) recomienda al MIT y a los tres investigadores no publicar nada sobre
este descubrimiento ni sobre nada relacionado.
El MIT y los investigadores ignoran las recomendaciones de la NSA y lo
publican en Junio de 1977 en Scientific American (versión española: Investigación y
Ciencia, octubre 1977), en un artículo titulado “Nuevas direcciones en criptografía”.
Más tarde publican RSA en Comms ACM (febrero 1978, vol 21, nº 2, pp. 120-126, una
publicación internacional). Debido a esta publicación los creadores R, S, A y los más
tarde formados PGP y RSADSI (RSA Data Security Inc) pierden la patente de RSA
fuera de Estados Unidos, esto es debido a que en la mayoría de los países hay que
obtener la patente antes de hacer la publicación, mientras que en Estados Unidos se
dispone de un año después de la publicación para solicitar la patente. Esto tendrá
posteriormente repercusiones en PGP. Otro asunto es que la ley norteamericana de
patentes es inusual porque permite la patente de algoritmos (lo usual es patentar un
sistema completo con una determinada finalidad). El sistema de criptografía RSA
probablemente no hubiese obtenido una patente en muchos otros países debido a que es
un algoritmo, y por lo tanto se habría considerado impatentable, incluso si R, S y A no
hubiesen tenido prisa debido a la interferencia de la NSA.
IDEA fue desarrollado por Xuejia Lai y James Massey en el ETH (Instituto
Suizo Federal de Tecnología) en Zurich. Hay muchos más cifradores simétricos,
simplemente se menciona aquí por su relación con PGP.
2.2 Nacimiento y evolución de PGP
En 1991 aparece “Senate Bill 266”, un proyecto de ley del Senado radical
anticrimen, que solicita “back doors” (puertas traseras) accesibles para el gobierno en
todas las herramientas de criptografía. Mientras esa ley era todavía debatida, Phil
Zimmermann combina varios métodos de cifrado para crear el software que apodó
Pretty Good Privacy o PGP.
-6-
PGP
Las ideas que subyacen bajo PGP eran conocidas y entendidas por informáticos
y matemáticos desde hace años, por lo tanto no hay una gran innovación en ese sentido.
La gran innovación aportada por PGP es hacer posible que esas herramientas se usen en
un ordenador de cualquier casa. Incluso las primeras versiones de PGP daban a la gente
con el sistema operativo DOS en casa el acceso a un grado-militar de cifrado. Mientras
“Senate Bill 266” todavía seguía su camino en el proceso legislativo, un amigo de
Zimmermann se encargó de distribuir PGP todo lo posible antes de que la ley entrase en
vigor. El software fue distribuido en una gran cantidad de sistemas BBS (“Bulletin
Board System“, Sistema de Tablón de Anuncios) así como en Internet (una gran red
académica y de investigación en aquel momento, pero con un alcance mundial). Su
activismo contribuyó a la desaparición de la legislación en contra de la criptografía.
Zimmermann, que había sido desde hacía mucho tiempo un activista antinuclear,
pensaba que PGP sería usado por disidentes, rebeldes y otra gente que se encontrara en
problemas debido a sus creencias, en otras palabras por mucha gente tanto dentro como
fuera de Estados Unidos. Desde la segunda guerra mundial, el gobierno de Estados
Unidos consideraba el cifrado “heavy-duty” (resistente) como una amenaza a la
seguridad nacional y no permitía su exportación fuera del país. Exportar software de
cifrado, incluido PGP, requería una licencia del Departamento de Estado, y algunos
países no podrían recibir dicho software bajo ningunas circunstancias. Estas reglas eran
conocidas como ITAR (“for Internacional Traffic in Arms Regulations”, regulaciones
para el tráfico internacional de armas) y clasificaban las herramientas de cifrado como
armas de guerra. Zimmerman decidió intentar evitar dichas restricciones
aprovechándose de la diferencia entre palabras escritas y software.
Fue el 5 de junio de 1991 Philip R. Zimmermann cuando publicó la versión final
de PGP 1.0. Implementó el cifrado RSA, combinado con un cifrador de claves simétrico
diseñado por él mismo y llamado Bass-O-Matic. Más tarde se dio cuenta de que BassO-Mastic era débil y decidió reemplazarlo por IDEA a partir de la versión 2.0. PGP 1.0
también usaba el algoritmo de resumen de mensajes MD4, posteriormente, Ron Rivest
diseñó MD5 para solucionar una debilidad descubierta en MD4, así PGP2.0 y las
siguientes versiones usarán MD5.
Zimmerman originalmente escribió PGP en texto normal (o código fuente),
simplemente como cualquier otro libro impreso, para evitar las leyes restrictivas
respecto al software criptográfico ya que los libros no se consideran software, incluso
aunque el libro contenga código fuente. Aunque muchos libros de criptografía tenían
restricciones a la hora de ser exportados, Zimmermann consiguió un permiso para
exportar su libro de código fuente. De esta forma cualquier persona, en cualquier parte
del mundo tenía la posibilidad de conseguir las instrucciones para construir su propio
software PGP. De hecho, enseguida se empezó a construir el software y PGP se
convirtió en un estándar de-facto para el cifrado de datos.
El gobierno de Estados Unidos consideró esto una táctica para evitar las
restricciones en exportación de municiones. El gobierno los denunció y durante los tres
años siguientes Zimmerman y la administración mantuvieron un proceso judicial.
Este juicio convirtió a Zimmerman en una especie de héroe en la comunidad
informática. Mucha gente descargó PGP solamente para saber de qué iba todo el
-7-
PGP
escándalo, y algunos terminaron usándolo. La defensa de Zimmerman difundió
mediáticamente el juicio en contra de PGP. En charlas sobre criptografía Zimmerman
leía cartas que había recibido de gente que se encontraba en regímenes opresivos y
zonas destrozadas por la guerra cuyas vidas habían sido salvadas gracias a PGP,
contribuyendo gratamente a que el público se diese cuenta de lo importante que había
sido su trabajo. PGP también estaba disponible en Internet antes de que el libro fuese
publicado, el código era accesible desde cualquier parte del mundo. El libro era
simplemente un dispositivo legal para hacer que la gente de fuera de Estados Unidos
tuviese la oportunidad de usar PGP sin quebrantar las leyes del país. Tras muchas
disputas legales el gobierno retiró los cargos por violación de leyes de exportación,
porque a fin de cuentas, él no exportó el programa.
Incluso sin el gobierno de Estados Unidos amenazando, PGP tuvo una serie de
problemas técnicos que los criptógrafos de diferentes lugares del mundo observaron. El
más evidente es que PGP hacía un gran uso de RSA y las técnicas de cifrado de IDEA,
los cuales tenían patente. Cualquiera que quisiese usar PGP comercialmente necesitaba
pagar las tasas de las licencia a los poseedores de las patentes. Muchos informáticos y
profesionales de la seguridad encontraron esto inaceptable porque querían un sistema de
cifrado que fuese gratis para el público general y para las empresas. El problema de las
patentes se solucionó con un cambio en las librerías del programa.
Durante 1991 y 1992 aparecen nuevas versiones de la primera hasta que en
mayo de 1992 se publica la versión 2.0 que fue la primera versión “real”, ya como
producto informático. Fue desarrollada por Zimmermann en colaboración con un grupo
de programadores de todo el mundo fuera de Estados Unidos para evitar problemas
legales.
En siguientes fechas van surgiendo diferentes versiones 2.x hasta que en julio
de 1993 se publica la versión 2.3a que se convierte en el primer sistema criptográfico
de-facto de correo electrónico. En agosto de ese año Zimmermann vende los derechos
para una versión comercial de PGP a la empresa ViaCrypt.
En 1994 el MIT participó en el desarrollo de las versiones 2.4, 2.5 y 2.6 y en
octubre se publicó la versión 2.62, a partir de la cual surgió la primera versión
internacional en 1995.
La creación de una versión internacional fue debido a que en USA se
consideraba delito la exportación de sistemas criptográficos de gran potencia igual que
lo es la exportación ilegal de armamento pesado. Para solucionar este problema un
noruego llamado Stale Schumacher descubrió que el código fuente escrito del programa
sí puede sacarse legalmente de Estados Unidos (consecuencia de las leyes que protegen
la libertad de prensa), algo de lo que ya se había aprovechado Zimmermann con
anterioridad. Así que, compró los libros que contenían dicho código, se los llevó a su
país, los recompiló mediante un sistema OCR de reconocimiento óptico de caracteres, y
reconstruyó el programa. El resultado es lo que se denomina "versión internacional" que
lleva una i tras el número de versión para distinguirlo de las versiones exportadas
ilegalmente. Esta versión internacional es legal al no haber sido compilada dentro de
USA ya que el código se obtuvo digitalizando libros impresos. A pesar de que se piense
que las versiones internacionales están “debilitadas” son igual de seguras que las de
Estados Unidos, sólo existen algunas diferencias como que se soportan claves RSA, los
-8-
PGP
servidores de claves están en Europa y no en Estados Unidos y se portaron a varias
plataformas nuevas.
La creación de múltiples interfaces (“shells”) por parte de diversos autores
permiten un uso más cómodo bajo Windows 3.1 Por fin llegan las modalidades para
Window 95/98: PGP 5.0, 5.5, 6.0, 6.5 y 7.0. También aparecen versiones para MAC.
Todo ello gracias al trabajo de Zimmermann y de su empresa PGP Inc, creada en 1.996
para la comercialización de los productos PGP y absorbida posteriormente por Network
Associates (NAI).
En 1998 Zimmerman ofreció una solución a muchos de los problemas legales,
cuando su compañía, PGP Corporation, presentó un diseño de PGP mejorado llamado
OpenPGP al “Internet Engineering Task Force” (IETF), el organismo responsable de los
estándares de Internet. OpenPGP definía estándares por los cuales diferentes programas
se podrían comunicar de forma segura usando una versión realzada del protocolo PGP y
diferentes algoritmos de cifrado, la descripción de este estándar está recogida en el RFC
2440. Esto llevó a que mucha gente y compañías creasen sus propias implementaciones
de OpenPGP, adaptándolas a sus propias necesidades.
En septiembre de 1999 el gobierno de Estados Unidos anunció el relajamiento
de las regulaciones sobre exportación de software criptográfico, y en diciembre la NAI
(Network Associates Inc) obtuvo una licencia de exportación de PGP hacia todo el
mundo. Tras varios años conviviendo la versión internacional y la versión de Estados
Unidos se empezó a usar en todo el mundo la versión estándar de PGP distribuida por la
PGP Corporation. Esto sigue así hasta el día de hoy, pero PGP ha ido evolucionando
con la aparición de nuevas versiones.
-9-
PGP
3. SOFTWARE
3.1. Obtención e instalación
Actualmente los derechos de PGP son de la compañía PGP Corporation. PGP
Corporation es una compañía fundada por Phil Zimmermann, uno de los más grandes
expertos a nivel mundial en cifrado de datos y, como ya se ha dicho, creador de PGP. Es
la mayor compañía del mundo en criptografía y seguridad de la información,
proporcionando software PGP para muchas plataformas diferentes.
PGP Corporation proporciona una implementación de OpenPGP que funciona
sobre los sistemas operativos más populares. Proporciona un sistema PGP que se integra
sin problemas con los clientes de correo estándares.
PGP es un producto comercial hoy en día y PGP Corporation proporciona un
gran rango de servicios relacionados. Los productos ofrecidos por PGP Corporation
son:
• PGP Desktop. Este módulo de PGP, incluye el cifrado de correo electrónico y
de discos duros. Mediante el componente PGPDisk, el sistema cifra las carpetas
que contienen los documentos de mayor sensibilidad, utilizando para ello la
tecnología de “disco virtual”, complementado con los algoritmos de mayor
robustez y de gran eficiencia en su ejecución, permitiendo así una operación
virtualmente transparente para el usuario final.
• PGP Keyserver. Este componente de PGP permite almacenar las llaves de
cifrado de la organización y las políticas centralizadas de configuración del PGP
Desktop instalado a cada usuario. Cada cliente se comunica con este servidor de
llaves para mantenerse actualizado y constituye el punto de referencia cuando no
se cuenta con la llave del usuario a quien se desea mandar correo cifrado.
• PGP Admin. Este módulo de PGP constituye la herramienta de configuración
del sistema. Permite al administrador definir una gran cantidad de parámetros de
instalación y operación de la aplicación Desktop que se instala a los usuarios
finales.
• ADK y “Key Reconstruction Server”. Entre las características más importantes
de PGP que se regulan desde la consola del administrador, merecen especial
mención la capacidad de manejar llaves adicionales de cifrado, también llamada
A.D.K (Additional Decryption Key), y el sistema de recuperación de claves
perdidas.
Desde la página www.pgp.com se puede bajar una versión de PGP Desktop de
prueba de 30 días, la versión que te permiten descargarte es la última, la 9.6. Todas las
versiones anteriores no comerciales y sus correspondientes internacionales se pueden
descargar de www.pgpi.com, al igual que de otras páginas, pero ésta es la página de
referencia.
- 10 -
PGP
La primeras versiones eran por línea de comandos y eran un poco engorrosas,
posteriormente se fueron integrando con los clientes de correo mediante plugins, aunque
a veces había problemas de compatibilidad.
Como hemos dicho la última la última versión existente es la 9.6 pero no ha
sido muy bien acogida entre los usuarios ya que es bastante compleja de utilizar. Una de
las más utilizadas y recomendadas es la 8.1 debido a su facilidad de uso y su fácil
integración con distintos clientes de correo actuales.
3.2. Proyectos “open source”
GnuPG es un proyecto de GNU, se trata de una implementación completa y libre
del OpenPGP estándar tal y como está definido en el RFC2440, que comenzó a
distribuirse en 1999 por el desarrollador alemán Werner Koch, la versión 1.0.0 fue
publicada el 7 de septiembre de 1999. Actualmente está disponible para Windows y
para Linux, así como para Mac-OS.
Ya que GnuPG sigue el estándar OpenPGP, puede ser usado para comunicarse
con gente que esté usando cualquier otro software que siga las especificaciones del
estándar. El nombre formal es GnuPG, pero mucha gente se refiere a él simplemente
como GPG.
GPG es una herramienta que funciona por línea de comandos, con características
que hacen fácil su integración con otras aplicaciones. Existen muchas interfaces gráficas
disponibles para utilizarlo.
Permite cifrar y firmar los datos, tiene un sistema de gestión de claves muy
versátil y módulos de acceso a los servidores de claves públicas. La versión 2 de
GnuPG también proporciona soporte para S/MIME.
GnuPG es software libre, lo cual quiere que decir que puede ser usado de forma
libre, modificado y distribuido, siempre bajo los términos de la a GNU General Public
License (Licencia Pública General de GNU).
•
•
Las dos versiones de GnuPG más populares son:
1.4.7: es la versión “standalone” más conocida y portable.
2.0.3: es la versión realzada y más difícil de instalar, es la más reciente.
El proyecto Gpg4win es el que proporciona una versión de GnuPG para
Windows y el proyecto Aegypten desarrolla la funcionalidad S/MIME en GnuPG2.
El uso de algoritmos con patentes restrictivas por parte de PGP representa un
problema en cuanto a la filosofía de GnuPG, la cual es la de implementar un sistema
criptográfico libre. Así pues, las patentes sobre estos algoritmos imposibilitan una
implementación total. Pero GnuPG también pretende cumplir con las reglas de los
estándares de OpenPGP. Existen unas extensiones para RSA e IDEA que pueden ser
instaladas y que permiten cierto uso de estos algoritmos.
- 11 -
PGP
4. MODO DE FUNCIONAMIENTO DE PGP
4.1 Sistemas de cifrado y caso concreto de PGP
A parte de los sistemas criptográficos clásicos existen dos tipos
fundamentalmente los simétricos o de clave privada y los asimétricos o de clave
pública. PGP usa un sistema híbrido que combina los dos. Empezaremos viendo las
características de cada uno por separado para después entender mejor la combinación de
ambos.
4.1.1. Cifrado simétrico (o de clave privada)
Cuando la clave de cifrado es la misma que la de descifrado (y, por tanto, los
algoritmos de cifrado y de descifrado coinciden) se habla de algoritmo de cifrado
simétrico. Este es el tipo de cifrado que ha dominado la historia de la criptografía hasta
hace un par de décadas.
Existen muchos algoritmos de clave simétrica resistentes al criptoanálisis: AES,
familia RC, Twofish, IDEA, familia CAST, Triple-DES, LOKI, por nombrar solamente
unos cuantos. Los algoritmos simétricos se clasifican en: algoritmos de cifrado en
bloque (block Chipre) y algoritmos de cifrado en flujo (stream Chipre).
Para cifrar, se coge el mensaje M y se le aplica la operación matemática Ck (es
decir, se usa el algoritmo de cifrado C con la clave k), obteniendo Ck(M). Para descifrar
el mensaje, se aplica la operación inversa Dk. Puesto que Ck y Dk son operaciones
inversas, se tiene Dk(Ck(M)) = M, esto es, el mensaje original. Esto requiere que el
emisor y el receptor del mensaje utilicen tanto el mismo algoritmo como la misma
clave.
Ahí radica uno de los problemas más importantes de este tipo de sistemas. La
comunicación segura entre el emisor y el receptor pasa porque ambos, y nadie más,
conozcan la clave k. En caso de que la clave se filtre en cualquier momento a un tercero
la seguridad desaparece. Una clave comprometida (es decir, que está o puede estar en
poder de un tercero) desbarata todo el sistema de comunicación segura basado en el
cifrado, ya que un posible “fisgón” además de poder ver la información puede suplantar
la identidad de los interlocutores.
Fig. 1: Cifrado simétrico
- 12 -
PGP
Los problemas de intercambiar y gestionar las claves se resuelven con los
sistemas de clave asimétrica o pública, que pasamos a ver a continuación.
4.1.2. Cifrado asimétrico (o de clave pública)
El problema de la distribución de claves se resuelve mediante la llamada
criptografía de clave pública, o de clave asimétrica, descubierta hacia 1975. Se basa en
matemáticas modulares y de exponentes.
En la criptografía de clave pública se utilizan dos claves distintas, una para el
cifrado y otra para el descifrado. La clave de cifrado es pública, esto es, conocida por
todo el mundo; la de descifrado (clave privada) solamente es conocida por su
propietario. Ambas constituyen un par de claves.
La particularidad de estas claves es que son reversibles, es decir, que ambas
sirven para cifrar o descifrar, pero son asimétricas, lo que supone que lo que se cifra con
la pública sólo se podrá descifrar con la privada y lo que se cifra con la privada sólo se
podrá descifrar con la clave pública. No es posible computacionalmente encontrar la
clave de descifrado únicamente a partir del algoritmo y la clave de cifrado. Esto se
puede aprovechar para enviar mensajes cifrados con la clave pública del receptor de
forma que sólo él podrá descifrar el mensaje ya que es el único que debería conocer su
clave privada. En realidad si es posible encontrar la clave de descifrado a partir de la de
cifrado, ya que la clave pública y privada no son independientes. Pero en la práctica, el
volumen de cálculos matemáticos que ha de realizarse es demasiado grande. Esto es
debido a que para la generación de las claves se usan funciones matemáticas de un solo
sentido (con trampa), de forma que en sentido directo los cálculos son sencillos pero en
sentido inverso se complican por haber varias posibilidades. Cuantas más posibilidades
haya más complicado será obtener la inversa. De ahí que la seguridad de estos sistemas
se base en el tamaño de las claves, que a partir de 1024 bits es ya bastante buena.
Por verlo con un ejemplo la criptografía de clave pública se asemeja a un buzón
de correos. Cualquiera puede introducir una carta en el buzón, pero solamente el
poseedor de la llave del buzón podrá abrirlo para acceder a su contenido.
El funcionamiento de este tipo de cifrado evita los peligros de enviar la clave por
un conducto inseguro, de hecho la clave pública puede ser tan diseminada como un
número de teléfono. Ahora un “fisgón” si conoce la clave pública de un interlocutor
sólo le servirá para enviarle mensajes y aunque conozca su clave privada sólo le
permitirá conocer el contenido de los mensajes que recibe pero no toda la conversación.
También permite aliviar los requisitos de almacenamiento de claves, sobre todo
cuando hay más personas comunicándose. Si hay N interlocutores, el número de claves
diferentes que hay que intercambiar y almacenar para comunicaciones seguras dos a dos
es N*(N-1)/2. Si N=100, eso significa más de 4.950 claves distintas. Por supuesto,
podemos hacer que algunas o todas las claves sean iguales, pero a lo mejor no es
conveniente que un participante tenga acceso a las comunicaciones entre otros dos
participantes. Con los sistemas de clave pública, cada usuario solamente necesita tener
una clave privada (la suya propia) y N-1 claves públicas.
- 13 -
PGP
En la actualidad, los sistemas de clave pública más utilizados son el RSA y el
Diffie-Hellman. Más correctamente, Diffie-Hellman es un algoritmo de intercambio de
claves. Su variante para criptografía de clave pública se conoce como "Algoritmo
Diffle-Hellman, Variante ElGamal".
Fig. 2: Cifrado asimétrico
Los criptosistemas de clave pública tampoco son la panacea universal, y
adolecen de diversos problemas, estos son el de la suplantación de identidad, el de
autenticidad, el de integridad y el que se refiere a la eficiencia.
Para solucionar los problemas de eficiencia vamos a ver ahora los sistemas de
cifrado híbrido. Más adelante veremos como solucionar los problemas de la autenticidad
e integridad mediante el proceso de firma digital y el de la suplantación de identidad
con los certificados digitales.
4.1.3. Cifrado híbrido (el que usa PGP)
Los algoritmos de clave pública son lentos, de hecho, suelen ser del orden de mil
veces más lentos que los algoritmos de clave simétrica. Los ordenadores son cada vez
más rápidos, pero cuando hay grandes cantidades de información por cifrar o descifrar
(pensemos, por ejemplo, en una base de datos protegida mediante cifrado) puede llegar
a ser una verdadera dificultad. También resulta que el tamaño del mensaje cifrado es
mucho mayor que el del original. Estos problemas, y algunos otros (por ejemplo, ciertos
ataques criptoanalíticos) se evitan mediante un sistema híbrido que tome lo mejor de
dos mundos.
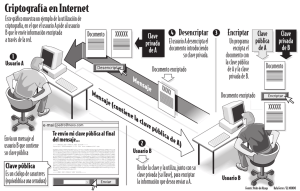
La idea radica en crear una clave simétrica con la que ciframos el mensaje a
enviar. A su vez, la clave simétrica es cifrada mediante la clave pública de un sistema
asimétrico. A la hora de enviar el mensaje, se enviará el propio mensaje cifrado y la
clave simétrica cifrada. De esta forma el receptor descifrará la clave simétrica usando su
clave privada y con la clave simétrica descifrará el contenido del mensaje. Siguiendo
este procedimiento hemos usado un sistema simétrico para cifrar el mensaje de forma
más eficiente y hemos compartido de forma segura la clave mediante un sistema
asimétrico (solucionando así los principales problemas de cada sistema).
Todavía se puede mejorar el proceso descrito eligiendo la clave simétrica K de
manera que sea distinta para cada comunicación, es decir, diferentes mensajes se cifran
con diferentes claves. Esto mejorará la seguridad de diversas maneras. En primer lugar,
- 14 -
PGP
un atacante puede obtener información (cuando menos, reducir la complejidad del
ataque) si sabe que diversos mensajes se cifran con la misma clave, aunque el atacante
no conozca cuál es dicha clave. También hay un riesgo asociado al hecho de que
siempre ciframos la misma clave simétrica K con la clave pública del destinatario.
Cambiar K de un mensaje a otro elimina estos peligros (reducidos pero que existen). Y
si el atacante lograra, por el medio que fuese, obtener K, solamente le serviría para un
solo mensaje, ya que el siguiente estaría cifrado con otra clave distinta. Por eso, la clave
simétrica "de usar y tirar" se denomina clave de sesión. Por supuesto, dicha clave ha de
ser aleatoria, para que no se pueda obtener información favorable a un posible atacante.
Este sistema híbrido utilizando claves de sesión es el que emplea PGP realmente
aunque para el usuario es transparente y se ve como un sistema asimétrico. En las
siguientes figuras se observa el proceso de cifrado y descifrado:
Fig. 3: Cifrado de un mensaje en un sistema híbrido
Fig. 4: Descifrado de un mensaje en un sistema híbrido
Mencionar también el caso en que un mensaje sea enviado a más de un receptor.
Para ello basta con añadir al mensaje la clave tantas veces como receptores y cada una
cifrada con la clave pública de cada uno de ellos. De esta forma cada receptor será
capaz de descifrar la que haya sido cifrada con su clave pública. Cualquiera que reciba
el mensaje a pesar de no ser destinado a él, como no tendrá ninguna clave privada
correspondiente a alguna de las claves cifradas añadidas al mensaje, no podrá descifrar
el contenido del mensaje. La capacidad de realizar esto viene dada por ADK (Additional
Decryption Key) que a su vez supone un problema de seguridad (que se comentará más
- 15 -
PGP
adelante) presente en las versiones 5.5.x a la 6.5.3.
Un esquema de este caso se puede ver a continuación:
Fig. 5: Mensaje cifrado para dos destinatarios diferentes
El diagrama anterior es conceptualmente correcto pero en realidad las claves
cifradas irían antes del comienzo del mensaje cifrado.
4.2 Algoritmos de cifrado empleados por PGP.
PGP utiliza distintas familias de algoritmos para las tareas fundamentales que
lleva a cabo. Éstas son la creación y cifrado de claves, el cifrado del mensaje y la firma
digital. Ya se han mencionado los más importantes cuando se describían los sistemas de
cifrado, ahora vamos a ver los que usa PGP.
4.2.1. Algoritmos de cifrado asimétricos.
Los sistemas de cifrado asimétricos intervienen en la generación del par de
llaves, en el cifrado de las claves de sesión y en el cifrado del hash del texto para
obtener la firma digital. Desde sus comienzos PGP usó el algoritmo RSA para este
propósito y en versiones posteriores apareció uno nuevo, una variante del algoritmo de
intercambio de claves, Diffie-Hellman, que se denomina “ElGamal”. A continuación
vamos a ver una descripción de ambos y los compararemos:
- 16 -
PGP
El algoritmo RSA es un algoritmo de clave pública desarrollado en 1977 en el
MIT por Ronald Rivest, Adi Shamir y Leonard Adelman. Fue registrado el 20 de
Septiembre de 1983. El 20 de Septiembre del 2000, tras 17 años, expiró la patente RSA,
pasando a ser un algoritmo de dominio público. Este popular sistema se basa en el
problema matemático de la factorización de números grandes.
El proceso de cifrado y el de firma es el mismo (en el primero se usa la clave
pública y en el segundo la privada) y su funcionamiento es el siguiente:
1. Inicialmente es necesario generar aleatoriamente dos números primos grandes, a
los que llamaremos p y q.
2. A continuación calcularemos n como producto de p y q: n = p * q
3. Se calcula fi: Φ(n)=(p-1)(q-1)
4. Se calcula un número natural e de manera que MCD(e, Φ(n))=1 , es decir, e
debe ser primo relativo de Φ(n).
Es lo mismo que buscar un número impar por el que dividir Φ(n) que de cero
como resto.
5. Mediante el algoritmo extendido de Euclides se calcula d: e*d mod Φ(n)=1
Puede calcularse d=((Y*Φ(n))+1)/e para Y=1,2,3,... hasta encontrar un d
entero.
6. El par de números (e,n) son la clave pública.
7. El par de números (d,n) son la clave privada.
8. Cifrado: La función de cifrado es C = M^e mod n
9. Descifrado: La función de descifrado es M = C^d mod n
Para poder romper RSA basta con factorizar n, una vez hecho esto obtenemos p
y q, y con estos Φ(n). Con estos datos ya podemos obtener la clave privada mediante el
algoritmo de Euclides extendido. Lo que puede parecer en principio algo trivial, no lo es
en absoluto. Si los números elegidos como claves son lo suficiente grandes (a partir de
1024 bits) resulta computacionalmente imposible factorizar estos números en un tiempo
razonable. Pues los algoritmos de factorización son de tiempo exponencial.
Actualmente uno de los algoritmos más rápidos de factorización es el conocido
como Number Field Sieve (NFS) aunque existen otros algoritmos muy rápidos como los
de curva elíptica, el algoritmo de Pollard, etc.
Aunque suene casi a ciencia ficción, existe un algoritmo para computadores
cuánticos que ha sido probado y demostrado por IBM y que permitiría reducir
enormemente la complejidad del problema de la factorización entera. Éste algoritmo es
conocido como “Algoritmo de Shor” y aunque facilitaría enormemente la ruptura de
claves RSA, seguiría siendo un problema muy complejo para claves grandes y
requeriría un ordenador cuántico bastante potente.
- 17 -
PGP
El algoritmo ElGamal (también conocido como algoritmo Diffie-Hellman,
variante ElGamal) se basa en la dificultad de calcular logaritmos discretos del grupo
multiplicativo en un campo finito. Fue descrito por Taher Elgamal en 1984 y está
basado en el algoritmo de intercambio de claves Diffie-Hellman (ideado en 1976), por
lo que si se puede romper uno de los dos se podrá romper el otro. El algoritmo ElGamal
fue ideado en un principio para producir firmas digitales, aunque después se extendió su
uso para utilizarlo en el cifrado de mensajes. El algoritmo ElGamal no se encuentra
patentado, sin embargo se considera que este algoritmo se encuentra cubierto por la
patente del algoritmo Diffie-Hellman ya se que se basa en él. Pero de todas formas esta
patente expiró el 29 de abril de 1997, por lo que ya es de libre uso.
Para generar un par de claves, se elige un número primo, p, y dos números
aleatorios, g y x, de modo que sean más pequeños que p. Se calcula: y = gx mod p
y la clave pública será y, g y p (grupos de usuarios pueden compartir g y p,
diferenciándose sólo en y). La clave privada será x.
El proceso de cifrado y de firma difiere, de hecho al proceso de firma se le
denomina DSS (Digital Signature Standard).
Para firmar un mensaje m el firmante realiza los pasos siguientes.
•
Selecciona un número aleatorio k tal que 0 < k < p − 1 y gcd(k,p − 1) = 1.
•
Calcula
•
•
Calcula
Si s = 0 reinicia el proceso.
.
.
El par (r,s) así obtenido es la firma digital de m. Para verificarla se hace del
siguiente modo:
•
Se verifica que 0 < r < p y que 0 < s < p − 1.
•
Se verifica que
.
El verificante acepta el mensaje únicamente si estas tres condiciones se cumplen.
Un tercero puede falsificar firmas si consigue la clave secreta x del firmante o si
encuentra colisiones en la función de Hash
considera que ambos problemas son suficientemente difíciles.
El proceso de cifrado de un mensaje es muy similar al de firmado:
•
•
se elige un número aleatorio, k, tal que k es relativamente primo a p-1.
se calcula a como:
a = g
•
k
mod p
(hasta este punto todo es idéntico)
se calcula b como:
b = y kM mod p
- 18 -
. Se
PGP
•
•
el mensaje cifrado está compuesto de a y b. El tamaño del texto cifrado es el
doble que el del texto original.
para descifrar el mensaje, hay que calcular:
M = b/ax mod p
El resultado es el mismo que el del algoritmo de intercambio de claves de DiffieHellman excepto en que y es parte de la clave y que lo cifrado se multiplica por yk.
Este algoritmo es probabilístico, significando que un solo texto plano se puede
cifrar a muchos textos cifrados posibles. La seguridad de ElGamal se basa, en parte, en
la dificultad de solucionar el problema discreto del logaritmo. En concreto, si este
problema se pudiera solucionar eficientemente, entonces ElGamal estaría roto. Sin
embargo, la seguridad de ElGamal confía realmente en la asunción supuesta por DiffieHellman.
Hay varias desventajas en usar DH frente a RSA:
a. Expansión del mensaje. El tamaño del mensaje cifrado se dobla respecto al
original. Esto sin embargo no es un obstáculo real en ElGamal ya que sólo se
utiliza para cifrar la clave de sesión de cada receptor.
b. Fortaleza de la firma. Las implementaciones actuales de DH sólo ofrecen
DSS como algoritmo de firmado. Esto limita la longitud de la clave a sólo
1024 bits lo que podría, por si solo, ser insuficiente para la seguridad a largo
plazo. Las firmas RSA utilizan una clave de hasta 2048 o 4096 bits
(dependiendo de la implementación).
c. Intensidad computacional. Tanto DH como DSS utilizan más intensamente
el tiempo de procesador que RSA. En los procesadores modernos esta
diferencia no es apreciable pero en dispositivos de poca potencia (tarjetas
inteligentes o pequeños chips) DH/DSS podrían no ser utilizables. Si el
tiempo de procesador o el tamaño de la clave son importantes un sistema
asimétrico basado en Curvas Elípticas podría ser una mejor elección que
tanto RSA como ElGamal.
d. La necesidad de una "buena" aleatoriedad. El valor aleatorio "k" en DH /
DSS necesita ser único e impredecible. Si se obtienen dos mensajes cifrados
con el mismo "k" o se recupera "k" entonces puede obtenerse la clave
privada.
La otra cara de la moneda es que hay varios beneficios en usar DH/DSS frente a
RSA:
a. Usando RSA, alguien podría generar un primo falso o de una clase especial
que facilitase su factorización. Existe un método para comprobar que los
números usados en DSA/DH se calculan aleatoriamente y son de hecho
primos.
b. No es apropiado usar RSA en situaciones en las que la generación de la clave
ocurre regularmente (en cada mensaje), como en sistemas de clave efímera.
- 19 -
PGP
c. RSA ofrece menos seguridad por cada bit de clave que DH/DSS.
d. DH parece estar basado en una teoría matemática más sólida.
DH requiere siempre un Generador de Números Aleatorios (RNG) seguro, pero
también lo necesita RSA. Un fallo en el RNG bajo RSA permitiría a un adversario
recuperar mensajes individuales, pero un fallo en el RNG usando DH / DSS permitiría
recuperar tanto el mensaje como la clave privada.
- Diferencias de rendimiento entre el cifrado RSA y ElGamal:
Cifrar
Descifrar
RSA-1024
(1024-bits)
8
93
ElGamal
(1024-bits, 160-bit exp.)
109
77
Tabla 1: Tiempos de cifrado (en milisegundos en una Sparc II)
- Diferencias de rendimiento al firmar con RSA o DSS:
RSA-1024 (e=3)
DSS-1024
43
.6
1100
0
7
27
7
6,500
Firmar
Verificar
Generar clave
Generar param.
Tabla 2: Tiempos firmado digital (en milisegundos en un Pentium Pro 200 MHz)
4.2.2. Algoritmos de cifrado simétricos.
Los sistemas de cifrado simétricos intervienen en el cifrado de los mensajes y
en el cifrado de la clave privada (para permitir su almacenamiento de una forma
segura). PGP ofrece varios algoritmos de este tipo: AES, CAST, TripleDES, IDEA y
Twofish.
IDEA (Internacional Data Encryption Algorithm). Fue desarrollado en Zurich
por James L. Massey y Xuejia Lai. La primera versión aparición en el año 1990 y más
tarde fue reforzado, en parte debido a la aparición, por las mismas fechas, del
criptoanálisis diferencial.
IDEA es un algoritmo de 8 rondas con un tamaño de bloque de 64 bits que
utiliza claves de longitud de hasta 128 bits. La fortaleza del cifrado la proporciona
"mezclar operaciones de diferentes grupos algebraicos". Actualmente, no se conoce
ninguna manera de romper IDEA aparte de la fuerza bruta, y la clave de tamaño 128
aporta una fuerte seguridad ante ataques de ese tipo.
Los mejores ataques conocidos contra IDEA son:
a. Ataque diferencial con clave elegida en una versión muy debilitada del
algoritmo con sólo 3 rondas.
- 20 -
PGP
b. Ataque temporizado sólo con texto cifrado y clave elegida sobre el algoritmo
completo que requiere 5x217 peticiones de claves relacionadas, cada una de
ellas usada para realizar 220 bloques de texto claro sin nombre y aleatorios.
c. Una combinación de criptoanálisis diferencial y lineal que requiere 229 pares
de texto en claro elegido y una carga de trabajo de 249 sumas módulo 216+1
en una versión muy debilitada del algoritmo con sólo 3 rondas.
d. Un ataque de criptoanálisis imposible por Biham y Shamir - los detalles son
esquemáticos (por decir algo) pero este es el mejor ataque contra IDEA hasta
la fecha.
Ninguno de estos ataques es útil para romper ninguna implementación práctica
de IDEA. IDEA completo resiste ataques diferenciales, lineales y con clave relacionada
o elegida, aunque hay un interesante ataque "lateral" que puede ser llevado a cabo en
una implementación de IDEA que permite medir tiempos de proceso con una alta
resolución.
Fig. 6: Una ronda del cifrado IDEA
IDEA ya no es el algoritmo por defecto en PGP debido a problemas de patente
(IDEA necesita una licencia para usarse comercialmente).
Triple-DES. Es una variación del algoritmo DES, pensada para aumentar su
seguridad y al mismo tiempo mantener la compatibilidad con las implementaciones ya
hechas de DES. Triple-DES consiste en aplicar DES tres veces con dos claves
diferentes, de la siguiente manera: en primer lugar se cifra el texto en claro empleando
la primera clave, después se descifra el criptograma obtenido con la segunda y
finalmente se vuelve a cifrar con la primera. Para descifrar el mensaje, el proceso es el
inverso: se descifra con la primera clave, se cifra con la segunda y se vuelve a descifrar
con la primera. Esto equivale a un cifrado con una clave de doble longitud
(evidentemente, cuando ambas claves son idénticas el cifrado sería equivalente a aplicar
DES con cualquiera de ellas).
Triple-DES tiene un tamaño de bloque de 64 bits y una longitud de clave de 168
(3*56) bits. Por la construcción de 3DES, se piensa que ofrece una seguridad
equivalente a un cifrado de bloque de 112 bits.
Los mejores ataques conocidos contra Triple-DES son:
- 21 -
PGP
a. El ataque Meet In The Middle (MITM) (encontrarse en el medio). Este
ataque puede ser teóricamente ser usado contra cualquier cifrado múltiple.
En el caso de DES este ataque requiere 524.288 Terabytes de
almacenamiento, 2112 cifrados y 2112 consultas de tabla.
b. Ataques MITM optimizados. Algunos compromisos tiempo/memoria
aplicados al ataque MITM estándar pueden hacer que MITM sea ligeramente
más realizable. Se necesitan 2108 operaciones de cualquier modo para el
ataque sea "realizable" en términos de memoria.
c. Ataque con clave relacionada. Necesita una consulta con clave relacionada,
una consulta con texto cifrado elegido y de 256 a 272 intentos de cifrado
offline.
Estos ataques no son útiles para romper implementaciones prácticas de TripleDES, a pesar de que el DES original fue reventado por fuerza bruta utilizando una
máquina especializada en sólo 56 horas. El Triple-DES se considera 256 veces más
difícil de romper que el DES original y como tal puede ser considerado seguro.
Fig. 7: Esquema funcionamiento Triple-DES
CAST es una familia de cifrados de bloque creada por Carlisle, Adams y
Stafford Tavares. Hay varias versiones de este algoritmo, las más conocidas son CAST128 o CAST5 y CAST-256 o CAST6. CAST5 es la más estándar, al que la gente se
refiere cuando dicen “CAST”. CAST-128 es un cifrador de 12 o 16 rondas que se basa
en la red de Feistel con bloques de 64 bits y tamaños de clave entre 40 y 128 bits (pero
con solo incrementos de 8 bits). Las 16 rondas completas se usan cuando la clave tiene
un tamaño mayor de 80 bits. Incluye unas largas S-Boxes de 8x32 bits basadas en
funciones bent, rotaciones dependientes de clave, adición y sustracción modular y
operaciones XOR. Hay tres tipos alternativos de funciones de ronda, pero son de
estructura similar y se diferencian sólo en la elección del tipo exacto de operación
(XOR, adición o sustracción) en varios puntos. CAST-256 derivó de CAST-128 que fue
candidato al proceso de selección para AES.
Como se ha mencionado previamente, CAST es una familia de cifrados.
Algunos de los algoritmos CAST con menos bits han sucumbido a ataques avanzados.
Pero no hay ataques conocidos contra las versiones más fuertes de CAST (la de 128 y
256 bits) con un número reducido de rondas - parece increíblemente seguro.
- 22 -
PGP
Fig.8: Tres rondas cifrado CAST-128
AES (Advanced Encryption Standard o estándar criptográfico avanzado) es la
búsqueda del gobierno de EE.UU. de un sustituto para el viejo estándar DES (Data
Encryption Standard o cifrado de datos estándar).
El Instituto de Estándares y Tecnología (NIST), hizo una primera solicitud
pública de algoritmos el 12 de Septiembre de 1997. Varios criptógrafos bien conocidos
(Rivest, Schneier, Knudsen, Biham, Rijmen, Coppersmith etc) desarrollaron algoritmos
candidatos para el AES que cumplían los criterios solicitados.
Los requisitos mínimos eran:
- El algoritmo debe ser de clave secreta (simétrico).
- El algoritmo debe ser un algoritmo de bloque.
- El algoritmo debe ser capaz de soportar las combinaciones clave-bloque de los
tamaños 128-128, 192-128 y 256-128.
De los 15 algoritmos iniciales, cinco (Mars, RC6, Rijndael, Serpent y Twofish)
fueron seleccionados para pasar a la segunda ronda. Finalmente el NIST en Octubre del
2000 adoptó el algoritmo diseñado por Joan Daemen y Vincent Rijmen como algoritmo
criptográfico no militar. Su elección, desarrollo y estudio se realizó de forma pública y
abierta.
- 23 -
PGP
Fig.9: Etapas cifrado AES
Twofish es un método de cifrado por bloques desarrollado por Counterpane
Labs y presentado al concurso AES del NIST. El tamaño de bloque en Twofish es de
128 bits y el tamaño de clave puede llegar hasta 256 bits. Twofish llegó a la ronda final
del concurso del NIST, pero no fue elegido para la estandarización. TwoFish quedó
tercero, tras Rijndael y Serpent.
Twofish fue diseñado por Bruce Schneier, John Kelsey, Doug Withing, David
Wagner, Chris Hall y Niels Ferguson. Twofish se relaciona con el método de cifrado
por bloques anterior Blowfish. Las características distintivas de Twofish son el uso de
S-boxes pre-computadas con llaves dependientes, y una llave-horario relativamente
compleja. Twofish coge prestados algunos elementos de otros diseños: por ejemplo, el
Pseudo-Hadamard Transforman (PHT) de la familia SAFER de cifrado. Twofish utiliza
la misma estructura de Feistel que el DES.
En la mayoría de las plataformas de software Twofish es levemente más lento
que Rijndael (el algoritmo elegido para AES) para las llaves de 128 bits, pero algo más
rápido para las llaves de 256 bits.
En fecha 2004, no se conoce un ataque contra Twofish más eficiente que la
búsqueda de claves por la fuerza bruta.
- 24 -
PGP
Fig.10: Funcionamiento TwoFish
Es difícil saber cuál es el mejor y más seguro de estos algoritmos pero ninguno
de ellos ha sido roto ni existen dudas serias sobre su fortaleza. PGP usa por defecto el
cifrado AES ya que ha sido fuertemente analizado y seleccionado de los mejores
algoritmos de cifrado simétricos. Pero PGP ofrece, además, todos los algoritmos
comentados arriba lo que da una mayor tranquilidad ya que en caso de que alguno fuera
roto, lo cual parece improbable actualmente, se podría deshabilitar y usar uno de los que
todavía fueran seguros.
4.2.3. Algoritmos de hash o de resumen.
Los algoritmos de hash intervienen en los procesos de firma digital (la firma
será el resultado de cifrar el resultado de la función hash) y el cifrado/descifrado de la
clave privada (se aplica hash a la frase de paso para genera una “huella digital” que es la
que se usa como clave para el cifrado/descifrado de la clave pública).
Una función hash o de resumen genera a partir de un mensaje, M, un resumen
del mismo, H(M). Esta función debe cumplir las siguientes características:
1. Unidireccionalidad: conocido un resumen H(M), debe ser
computacionalmente imposible encontrar M a partir de dicho resumen.
2. Compresión: a partir de un mensaje de cualquier longitud, el resumen H(M)
debe tener una longitud fija. Lo normal es que la longitud de H(M) sea menor
que el mensaje M.
3. Facilidad de cálculo: debe ser fácil calcular H(M) a partir de un mensaje M.
4. Difusión: el resumen H(M) debe ser una función compleja de todos los bits
del mensaje M, de tal forma que simplemente modificando un solo bit del
mensaje M, el hash H(M) debería cambiar radicalmente (al menos la mitad de
sus bits).
5. Colisión simple: conocido M, será computacionalmente imposible encontrar
otro M’ tal que H(M) = H(M’). Esto se conoce como resistencia débil a las
colisiones.
- 25 -
PGP
6. Colisión fuerte: será computacionalmente imposible encontrar un par (M, M’)
de forma que H(M) = H(M’). Esto se conoce como resistencia fuerte a las
colisiones.
PGP ofrece varias funciones de hash MD-5, RIPEMD-160, SHA-1 y varias
versiones de de SHA-2 (de 256, 384 y 512 bits).
MD5 (acrónimo de Message-Digest Algorithm 5, Algoritmo de Resumen del
Mensaje 5) es un algoritmo de reducción criptográfico de 128 bits ampliamente usado.
Fue diseñado por Ronald Rivest cuando un análisis indicó que el algoritmo MD4 era
inseguro y se decidió a programar el MD5 para sustituirlo en 1991. Las debilidades en
MD4 fueron descubiertas por Hans Dobbertin. En 1996 Dobbertin anunció una colisión
de hash de la función de compresión del MD5. Esto no era un ataque contra MD5, pero
hizo que los criptógrafos empezasen a recomendar el reemplazo de la codificación MD5
a otras como SHA-1 o RIPEMD-160. En Agosto de 2004 unos investigadores chinos
encontraron también colisiones hash en el MD5. Actualmente el uso de MD5 es muy
amplio y se desconoce cómo afectarán estos problemas a su uso y a su futuro pero para
empezar a pesar de haber sido incluido desde el principio en PGP, ahora no se
recomienda su uso por razones de seguridad.
Los siguientes cinco pasos son efectuados para calcular el resumen de un
mensaje.
•
Paso 1. Añadiendo bits.
El mensaje será extendido hasta que su longitud en bits sea congruente con 448,
módulo 512. Esto es, el mensaje se extenderá hasta que se forme el menor
número múltiplo de 512 bits. Esta extensión se realiza siempre, incluso si la
longitud del mensaje es ya congruente con 448, módulo 512.
La extensión se realiza como sigue: un sólo bit "1" se añade al mensaje, y
después bits "0" se añaden hasta que la longitud en bits del mensaje extendido se
haga congruente con 448, módulo 512. En todos los mensajes se añade al menos
un bit y como máximo 512.
•
Paso 2. Longitud del mensaje
Una representación de 64 bits de 'b' (la longitud del mensaje antes de añadir los
bits) se concatena al resultado del paso anterior. En el supuesto no deseado de
que 'b' sea mayor que 264, entonces sólo los 64 bits de menor peso de 'b' se
usarán.
En este punto el mensaje resultante (después de rellenar con los bits y con 'b') se
tiene una longitud que es un múltiplo exacto de 512 bits. A su vez, la longitud
del mensaje es múltiplo de 16 palabras (32 bits por palabra). Con M[0 ... N-1]
denotaremos las palabras del mensaje resultante, donde N es múltiplo de 16.
- 26 -
PGP
•
Paso 3. Inicializar el búfer MD
Un búfer de cuatro palabras (A, B, C, D) se usa para calcular el resumen del
mensaje.
Aquí cada una de las letras A, B, C, D representa un registro de 32 bits. Estos
registros se inicializan con los siguientes valores hexadecimales, los bits de
menor peso primero:
palabra A: 01 23 45 67
palabra B: 89 ab cd ef
palabra C: fe dc ba 98
palabra D: 76 54 32 10
•
Paso 4. Procesado del mensaje en bloques de 16 palabras
Primero definimos cuatro funciones auxiliares que toman como entrada tres
palabras de 32 bits y su salida es una palabra de 32 bits.
Los operadores
respectivamente.
son las funciones XOR, AND, OR y NOT
En cada posición de cada bit F actúa como un condicional: si X, entonces Y sino
Z. La función F podría haber sido definida usando + en lugar de v ya que XY y
not(x) Z nunca tendrán unos ('1') en la misma posición de bit. Es interesante
resaltar que si los bits de X, Y y Z son independientes y no sesgados, cada uno
de los bits de F(X,Y,Z) será independiente y no sesgado.
Las funciones G, H e I son similares a la función F, ya que actúan "bit a bit en
paralelo" para producir sus salidas de los bits de X, Y y Z, en la medida que si
cada bit correspondiente de X, Y y Z son independientes y no sesgados, entonces
cada bit de G(X,Y,Z), H(X,Y,Z) e I(X,Y,Z) serán independientes y no sesgados.
Nótese que la función H es la comparación bit a bit "xor" o función "paridad" de
sus entradas.
Este paso usa una tabla de 64 elementos T[1 ... 64] construida con la función
seno. Denotaremos por T[i] el elemento i-ésimo de esta tabla, que será igual a la
parte entera del valor absoluto del seno de 'i' 4294967296 veces, donde 'i' está en
radianes.
RIPEMD-160 (acrónimo de RACE Integrity Primitives Evaluation Message
Digest, primitivas de integridad del resumen del mensaje) es una función criptográfica
de hash de 160 bits desarrollado en Europa por Hans Dobbertin, Antón Bosselaers y
- 27 -
PGP
Bart Preneel, publicada en 1996. Es una versión mejorada de RIPEMD, que estaba
basado sobre los principios del diseño del algoritmo MD4, y es similar en seguridad y
funcionamiento al SHA-1.
También existen versiones de 128, 256 y 320 bits de este algoritmo, llamadas
RIPEMD-128, RIPEMD-256 y RIPEMD-320 respectivamente. La versión de 128 bits
fue pensada solamente como un reemplazo para el RIPEMD original, que eran también
de 128 bits, y en la que habían sido encontradas razones para cuestionar su seguridad.
Las versiones de 256 y 320 bits solamente disminuyen la posibilidad de colisiones hash
accidentales, y no tienen niveles más altos de seguridad con respecto a RIPEMD-128 y
RIPEMD-160. En agosto del año 2004, una colisión hash fue divulgada para el
algoritmo RIPEMD original que no afecta al resto de algoritmos.
RIPEMD-160 fue diseñado en la comunidad académica abierta, en contraste con
el algoritmo SHA-1, diseñado por la Agencia de Seguridad Nacional estadounidense
(NSA). Por otra parte, RIPEMD-160 es un diseño menos popular y por lo tanto está
peor estudiado. No existe ninguna patente asociada al RIPEMD-160.
La familia SHA (Secure Hash Algorithm, Algoritmo de Hash Seguro) es un
sistema de funciones hash criptográficas relacionadas de la Agencia de Seguridad
Nacional de los Estados Unidos y publicadas por el National Institute of Standards and
Technology (NIST). El primer miembro de la familia fue publicado en 1993 y es
oficialmente llamado SHA. Sin embargo, hoy día, no oficialmente se le llama SHA-0
para evitar confusiones con sus sucesores. Dos años más tarde el primer sucesor de
SHA fue publicado con el nombre de SHA-1. Existen cuatro variantes más que se han
publicado desde entonces cuyas diferencias se basan en un diseño algo modificado y
rangos de salida incrementados: SHA-224, SHA-256, SHA-384, y SHA-512 (todos
ellos son referidos como SHA-2). SHA-0 y SHA-1 producen una salida resumen de 160
bits de un mensaje que puede tener un tamaño máximo de 264 bits, y se basa en
principios similares a los usados en el diseño de los algoritmos de resumen del mensaje
MD4 y MD5.
En 1998, un ataque a SHA-0 fue encontrado pero no fue reconocido para SHA1, se desconoce si fue la NSA quien lo descubrió pero aumentó la seguridad del SHA-1.
SHA-1 ha sido examinado muy de cerca por la comunidad criptográfica pública, y no se
ha encontrado ningún ataque efectivo. No obstante, en el año 2004, un número de
ataques significativos fueron divulgados sobre funciones criptográficas de hash con una
estructura similar a SHA-1; esto ha planteado dudas sobre la seguridad a largo plazo de
SHA-1.
La resistencia del algoritmo SHA-1 se ha visto comprometida a lo largo del año
2005. Después de que MD5, entre otros, quedara seriamente comprometido en el 2004
por parte de un equipo de investigadores chinos, el tiempo de vida de SHA-1 quedó
visto para sentencia.
El mismo equipo de investigadores chinos, compuesto por Xiaoyun Wang,
Yiqun Lisa Yin y Hongbo Yu (principalmente de la Shandong University en China), ha
demostrado que son capaces de romper el SHA-1 en al menos 269 operaciones, unas
2000 veces más rápido que un ataque de fuerza bruta (que requeriría 280 operaciones).
Los últimos ataques contra SHA-1 han logrado debilitarlo hasta 263. A pesar de que 263
- 28 -
PGP
suponen aún un número alto de operaciones, se encuentra dentro de los límites de las
capacidades actuales de cálculos, y es previsible que con el paso del tiempo romper esta
función sea trivial, al aumentar las capacidades de cálculo y al ser más serios los ataques
contra SHA-1.
A pesar de que el NIST contempla funciones de SHA de mayor tamaño (por
ejemplo, el SHA-512, de 512 bits de longitud) se habla de buscar una nueva función
hash estandarizada que permita sustituir a SHA-1.
Actualmente, en PGP por defecto vienen deshabilitadas las funciones MD5,
SHA-1 y RIPEMD-160, dando preferencia a las de SHA-2, pero se pueden usar
cualquiera de ellas. Este hecho de tener varias funciones de hash donde escoger, igual
que en el caso de los algoritmos de cifrado, dota de mayor seguridad a PGP ya que si
una pasa a ser insegura se podrá usar cualquiera de las otras.
4.3 Firma digital.
Mencionamos con anterioridad que los problemas de integridad y autenticidad
(el de no repudio va asociado a éste) quedaban sin resolver en los sistemas asimétricos e
híbridos.
En un principio para poder conseguir estos tres servicios se nos podría ocurrir
realizar un hash del mensaje a enviar y adjuntarlo a dicho mensaje. En este caso la
integridad se cumpliría ya que en caso de modificar cualquier dato del mensaje el hash
dejaría de coincidir con el enviado. Pero la autenticidad no se cumple (y, por
consiguiente, el no repudio tampoco) dado que cualquiera podría generar el hash del
mensaje. En realidad tampoco se conseguiría realmente la integridad ya que cualquiera
podría capturar el mensaje, modificarlo, recalcular el hash y reenviarlo sin que el
destinatario tenga forma de saber que la modificación ha ocurrido.
La característica más importante de una firma es que sólo pueda ser producida
por un único firmante, de forma que una firma concreta identifique unívocamente a un
usuario, de igual forma, que una secuencia de ADN concreta pertenece a una persona en
concreto y sólo una. Por lo tanto necesitamos algo que sea inherente a la persona. Si
pensamos en algo que sea único en los sistemas asimétricos a poco que conozcamos de
ellos nos daremos cuenta que ese algo es la clave privada.
Debido a la característica de que las claves pública y privada son reversibles (lo
que cifra una lo descifra la otra) podríamos cifrar parte del mensaje con la clave privada.
Haciendo esto se garantizaría que el mensaje sólo puede haber sido enviado por una
única persona, el poseedor de la clave privada. Ese algo que se cifra va a ser el hash del
texto inicial, ya que cifrar todo el mensaje sería poco eficiente ya que el documento
resultante aumenta de tamaño. Además podría ser el origen de algún ataque
criptoanalítico ya que cifrando un mensaje cuidadosamente compuesto se podría obtener
mucha información sobre la clave privada del que cifra. Y evidentemente si ciframos y
firmamos el mensaje (en ese orden o en el inverso) estaríamos aplicando la clave
privada y la pública al mismo texto, con lo que ambos procesos se anularían acabando
con el mensaje original tal cual, así que habría que escoger entre cifrar o firmar.
- 29 -
PGP
El hash es una función H que toma un mensaje M y produce un condensado de
éste H(M)=h. Está función se denomina también de resumen y ya se han comentado sus
propiedades en el apartado de algoritmos, además de ver ejemplos concretos de éstos.
En resumen, el proceso de firma consiste en:
- Tomar el mensaje M que se desea enviar y aplicarle la función resumen,
obteniendo H(M)=h.
- Aplicar al resumen la clave privada ks del usuario que envía el mensaje. El
resultado es la firma digital: Cks(h).
Fig. 11: Proceso de firma
Se enviará conjuntamente el mensaje M y la firma Cks(h). Para verificar la firma
se procederá del siguiente modo:
- Aplicar la clave pública kp del usuario que envió el mensaje a la firma Cks(h).
El resultado es Ckp(Cks(h))=h.
- Aplicar al mensaje la función resumen, obteniendo H(M)=h'.
- Comparar el resultado de los dos pasos anteriores. Si coinciden (h=h´), la firma
será correcta.
Fig. 12: Proceso de verificación de la firma digital
La verificación de la firma dependerá tanto de que haya sido realizada con la
clave correcta como de que el mensaje no se haya alterado. De ese modo comprobamos
a la vez que el mensaje fue firmado efectivamente por el usuario que envía el mensaje
(autenticidad) y por lo tanto no podrá negar que lo haya enviado él (no repudio) y que
dicho mensaje no ha sido alterado con posterioridad (integridad).
Si deseamos efectuar las operaciones de cifrar y firmar, podemos hacerlo sin
problemas. El orden seguido por PGP es primero firmar y luego cifrar. Es decir, el
- 30 -
PGP
usuario primero creará su firma Cks(h), y posteriormente cifrará el paquete M´ = {M,
Cks(h)}.
Como ya hemos dicho con la firma digital se solucionan los problemas de
integridad y autenticidad (y por lo tanto el no repudio) pero aún nos queda el problema
de suplantación de identidad, es decir, saber si las claves que se están usando pertenecen
realmente al usuario con el que se establece la comunicación. Esto se solucionará con
los certificados digitales y los mecanismos de validez y confianza usados en PGP.
4.4 Certificados digitales
Una cuestión a tener en cuenta acerca de los sistemas criptográficos de clave
pública es que un usuario debe de asegurarse que está cifrando los mensajes con la clave
correcta. En un entorno donde se intercambian claves a través de servidores públicos se
está expuesto a ataques. Alguien podría enviar un mail cifrado con una clave falsa
asociada al nombre e identificador de usuario del receptor previsto, con lo que supone
que el mail irá al receptor deseado, pero lo que ocurre es que los datos cifrados son
interceptados por el dueño de la clave falsa. Es decir es vital asegurarse que la clave
pública con la que ciframos el mensaje es, realmente, la clave pública de la persona a la
pretendemos mandarlo. A este problema se le llama problema de la suplantación y es el
talón de Aquiles de la criptografía de clave pública.
Los certificados digitales simplifican la tarea de establecer si una clave pública
realmente pertenece a su aparente dueño. Un certificado es una forma de credencial,
como podría ser el carne de conducir, el DNI…, los cuales tienen información
identificándote y dicha información ha sido confirmada por alguien, de tal forma que
asegura que te pertenece realmente. Un certificado digital es algo similar a un
certificado físico. Un certificado digital es la información de una persona junto con su
clave pública que ayuda a otros a verificar que la clave es válida. Los certificados
digitales son usados para evitar intentos de sustitución de la clave de una persona por
otra falsa.
Un certificado digital consiste en tres cosas:
• Una clave pública.
• Información del propietario.
• Una o más firmas digitales.
El propósito de la firma digital de un documento es establecer que la
información del certificado ha sido avalada por alguna otra persona o entidad. La firma
digital no avala la total autenticidad del certificado, sino que sólo responde por el hecho
de que la información va con la clave.
- 31 -
PGP
Fig.13: Anatomía de un certificado
4.4.1. Distribución de de certificados
Los certificados se utilizan cuando es necesario intercambiar claves públicas con
alguien más. Para pequeños grupos de gente que desean comunicarse de forma segura
es fácil cambiar las claves públicas en persona o a través de medios seguros, esto se
llama distribución manual de claves públicas. Más allá de ese punto es necesario poner
sistemas que proporcionen los necesarios mecanismos de seguridad, almacenamiento e
intercambio, para que la gente pueda comunicarse en caso de ser necesario. Pueden ser
en forma de repositorios de almacenamiento llamados ‘Servidores de Certificados’, o
sistemas más estructurados que proporcionen características de manejo de claves, los
cuales se llaman ‘Infraestructuras de Clave Pública’ o Public Key Infrastructures
(PKIs).
4.4.2. Formatos de certificados
Como ya se ha dicho, un certificado digital es básicamente una colección de
información de identificación, junto con clave pública, y todo esto firmado por una
tercera parte de confianza, para probar su autenticidad. Un certificado digital puede
tener distintos tipos de formatos.
Actualmente PGP reconoce dos tipos de formatos de certificados, aunque en su
origen sólo eran reconocidos los certificados PGP. Los dos tipos de formatos
reconocidos por PGP son:
•
Certificados PGP: podemos verlo como una clave pública con una o más
etiquetas vinculadas a ella. En estas ‘etiquetas’ encontrarás información que
identifica al propietario de la clave y la firma de éste, mediante su clave privada,
con lo que establece que la clave y la identificación van juntas (esta firma se
llama ‘self-signature’, propia firma, todos los certificados poseen este tipo de
firma). Esta firma establece autenticidad, por lo menos para el usuario de la
- 32 -
PGP
clave. Desde PGP 5.0 cada identificador de usuario es automáticamente firmado
con la clave privada del propio usuario, en las anteriores versiones había que
hacerlo manualmente.
Otro aspecto del formato de un certificado PGP es que un único certificado
puede contener múltiples firmas. Diferentes personas pueden firmar el par
clave/identificador para avalar que la clave pertenece sin duda al dueño
especificado. Los certificados pueden tener más información sobre el usuario, a
parte del identificador, como pueden ser su nombre, empresa, foto…
Fig. 14: Un certificado PGP
•
Certificados X.509: es otro formato muy común de certificados. Todos los
certificados X.509 siguen el estándar internacional ITU-T X.509, de esta forma
(teóricamente), certificados X.509 creados por una aplicación pueden ser usados
por cualquier aplicación que siga el estándar de este tipo de certificados. En la
práctica hay compañías que han creado sus propias versiones de X.509, por lo
que no se pueden usar esos certificados en otras aplicaciones.
Para obtener la validez del certificado es necesario que alguien asegure
que la clave pública y el identificador del propietario van juntos. Con los
certificados PGP, cualquiera puede llevar a cabo ese papel, pero los certificados
X.509, deben validados siempre una Autoridad Certificadora o alguien
designado por esta.
Para obtener un certificado X.509, debes solicitarlo a una Autoridad
Certificadora. Tienes que proporcionarles tu clave pública, una prueba de que
posees la correspondiente clave privada y alguna información sobre ti mismo.
Posteriormente firmas digitalmente la información y mandas el paquete a la
Autoridad Certificadora. La autoridad correspondiente realiza las gestiones
necesarias para verificar que los datos que le has proporcionado son correctos, y
en caso de que lo sean, genera el certificado y te lo envía.
- 33 -
PGP
Fig. 15: Un certificado X.509
4.4.3 Validez y confianza
Cada usuario de un sistema de clave pública esta expuesto a confundir una clave
falsa con una real. Validez es la propiedad que certifica que una clave pública pertenece
al aparente propietario. La validez es esencial en los entornos de clave pública donde
hay que comprobar constantemente si un certificado es o no auténtico. Cuando te has
asegurado de que el certificado perteneciente a alguien es válido puedes firmar su copia
en tu anillo para avalar el hecho de que has comprobado que el certificado es auténtico.
Si quieres que otros sepan que has avalado a esa persona puedes exportar la firma a un
servidor de certificados, de tal forma que los otros podrán verlo.
La confianza se refiere al propietario de la clave. Tienes confianza en una clave
si crees que el dueño es responsable a la hora de asegurarse de que los datos son
correctos antes de firmar un certificado. Si confiamos en una persona y esa persona
valida un certificado, nosotros consideraremos ese certificado válido, a pesar de no
habernos asegurado nosotros mismos que los datos eran correctos. No debemos de
confundir validez y confianza, ya que se refieren a cosas distintas, la validez a la clave y
la confianza al propietario. Por ejemplo una clave puede ser válida porque está asociada
al usuario correcto, pero sin embargo tú no tienes la confianza suficiente en ese usuario
para fiarte si te dice que otra clave es válida.
4.4.4. Modelos de confianza
El modelo de confianza es la forma en la que se confía en la validez de
certificados. Hay tres modelos diferentes de confianza:
- 34 -
PGP
•
Confianza directa (Direct Trust): es el modelo más sencillo. En este modelo
un usuario considera una clave válida porque sabe de donde viene. En PGP sería
alguien que sólo considera válidas las claves que valida él y nunca confía en
claves validadas por otras personas.
Fig. 16: Confianza directa
•
Jerarquía de confianza (Hierarchical Trust): en este modelo hay un número
de certificadores raíz de los cuales se extiende la confianza. Estos certificadores
pueden validar certificados ellos mismos o delegar en otros certificadores para
que lo hagan. Podemos verlo como un árbol de confianza donde la validez de los
certificados de las hojas tiene que ser proporcionada por alguien en una posición
superior en el árbol, subiendo por el árbol se acabará en una certificadora raíz.
Fig. 17: Jerarquía de confianza
•
Red de confiaza (Web of Trust): este modelo engloba los dos anteriores, pero
también añade el concepto de que ‘la confianza está en los ojos del que mira’ y
la idea de cuanta más información mejor. Es un modelo de confianza
acumulativo. Se puede validar directamente en un certificado o a través de una
cadena.
Este es el modelo más utilizado en PGP, en el cual cualquier usuario puede
validar el certificado de otro. De todas formas ese certificado sólo será válido
para otro usuario si confía en el que lo validó. De esta forma cada uno construirá
su propia red de confianza.
- 35 -
PGP
PGP permite adaptarse igual de bien a una estructura jerárquica basada en ACs
que a una red de confianza descentralizada, aunque fue creado pensado en esta
última posibilidad. En palabras de su autor, "PGP es para aquellas personas que
prefieren plegar su propio paracaídas." Permite una mayor flexibilidad y
capacidad de elección.
4.4.5. Niveles de confianza en PGP
Existe en PGP un nivel de confianza, llamado confianza implícita, el cual es la
confianza en tu propio par de claves. PGP asume que si tú posees la clave privada debes
confiar en todas las acciones relativas a tu clave pública.
Hay tres niveles de confianza que se pueden asignar a la clave pública de
alguien:
•
•
•
Confianza completa.
Confianza marginal.
No confianza.
También hay tres niveles de validez en PGP:
•
•
•
Válido.
Marginalmente válido.
Inválido.
Para definir la confianza en una clave pública:
•
•
La clave debe ser válida, ya haya sido validada por ti o por alguien de tu
confianza.
Estableces el nivel de confianza el propietario de la clave.
PGP permite configurar lo que entendemos por una firma fiable, por ejemplo
con una firma de confianza completa sería suficiente para validar una clave, pero serían
necesarias varias marginales, el número podría depender, según nuestra propia elección.
4.4.6. Revocación de certificados
Los certificados sólo son útiles mientras son válidos. Es inseguro asumir que un
certificado es válido para siempre. En la mayoría de las organizaciones y en todas las
PKIs, los certificados tienen un tiempo de vida limitado. Este tiempo suele ser el que se
consideraría necesario para que la clave se viese comprometida.
Los certificados son creados con una duración determinada, tienen una fecha de
comienzo y una fecha de caducidad. Durante todo ese tiempo el certificado puede ser
utilizado. Cuando caduque no será válido, ni se podrá usar el par clave/identificador. De
todas formas el certificado puede ser usado para recuperar información cifrada o
firmada durante el periodo de validez.
- 36 -
PGP
Hay también situaciones donde puede ser necesario invalidar un certificado, a
pesar de que no se haya alcanzado la fecha de caducidad de éste. Esto es llamado
revocación. Cualquiera que haya firmado un certificado puede revocar su firma en él,
siempre que sea con la misma clave privada con la que lo firmó. Se revocará un
certificado en caso de sospechar que haya sido comprometido. Los certificados
revocados no son ya usables y carecen de los compromisos de los caducados.
Con los certificados X.509, el hecho de revocar una firma quiere decir
prácticamente lo mismo que revocar el certificado, debido a que solamente está firmado
por una Autoridad Certificadora.
Sólo el dueño del certificado (el poseedor de la clave privada) o alguien al que
éste ha designado como ‘revocador’ puede revocar un certificado PGP.
Cuando un certificado es revocado es importante hacer conocedora al resto de la
gente de que el certificado ya no es válido. Con los certificados PGP la forma más
sencilla de comunicarlo es publicarlo en un servidor de certificados, para que los demás
usuarios estén advertidos y no usen la clave pública. Con los certificados X.509 es la
Autoridad Certificadora la encargada de enviar regularmente a todos los usuarios una
Lista de Revocación de Certificados (CRL, ‘Certification Revocation List’).
4.5 Anillo de claves.
PGP guarda las claves de forma cifrada en dos ficheros en el disco duro, uno
para claves públicas y otro para claves privadas. Estos ficheros se llaman anillos o
llaveros. Las claves públicas de todos tus receptores se almacenarán en tu anillo público
y tus claves privadas en tu anillo privado. Si se pierde el anillo privado será imposible
descifrar cualquier información cifrada con claves de dicho anillo.
Estructura del anillo de claves privadas (tabla 3):
Sellado de tiempo
Clave ID*
Clave pública
Clave privada cifrada
ID usuario
T1
e1 mod 264
Clave púb. 1
Clave priv. 1
Usuario 1
---
---
---
---
Ti
ei mod 264
ei
EH(FPi)(di)
---
---
---
---
Tn
en
mod
264
Clave púb. n
Clave priv. n
--Usuario i
--Usuario n
Campos del los anillo de claves pivadas:
• Sellado de tiempo: Fecha y hora de la generación del par de claves.
• Clave ID: Identificador de clave (últimos 64 bits de la clave pública “e”).
• Clave pública.
• Clave privada cifrada: Cifra EH (FPi) de la clave privada d con un
algoritmo simétrico y la función hash de la frase de paso del propietario
como clave secreta.
- 37 -
PGP
•
ID usuario: Identificación del usuario, normalmente dirección de email.
Estructura del anillo de claves públicas (tablas 4 y 5):
Sellado de tiempo
Clave ID*
Clave pública
Confianza propietario
ID usuario
T1
e1 mod 264
Clave púb. 1
flag_confianza 1
Usuario 1
---
---
---
---
Ti
ei mod 264
ei
flag_confianza i
---
---
--Tn
en
--mod
264
Clave púb. n
flag_confianza n
Legitimación de clave
Firma(s)
Confianza de Firmas
flag_confianza 1
•••
•••
---
---
---
flag_confianza i
•••
•••
---
---
---
flag_confianza n
•••
•••
--Usuario i
--Usuario n
(*) Se usa este campo para la indexación de la tabla en ambos anillos.
Campos nuevos en el anillo de claves públicas:
•
•
•
•
Confianza propietario: el nivel de confianza del usuario en el propietario de
la clave.
Legitimación de la clave: validez de la clave por parte del usuario.
Firmas: otros usuarios que han firmado el certificado.
Confianza: nivel de confianza en esas firmas.
- 38 -
PGP
5. MODO DE FUNCIONAMIENTO
5.1 Creación de las claves
Una clave es un valor que trabaja con un algoritmo criptográfico para cifrar un
texto. Las claves son básicamente números realmente grandes. El tamaño de la clave
está medido en bits. En criptografía de clave pública cuanto más grande es la clave, más
seguro es el cifrado.
Aunque la clave pública y la privada están matemáticamente relacionadas, es
muy complicado obtener una a partir de la otra, de todas formas dando el tiempo y los
recursos computacionales necesarios es posible averiguarla. Esto hace que sea muy
importante elegir correctamente el tamaño de la clave, lo suficientemente larga para que
sea segura, pero lo suficientemente corta para que sea aplicada lo suficientemente
rápido.
Las claves privadas son almacenadas de forma cifrada. PGP guarda las claves en
dos archivos en el disco duro, uno para las claves públicas y otro para las privadas, estos
archivos se llaman anillos.
Cada usuario debe generar su pareja de claves. Para ello es necesario introducir
el nombre, la dirección de correo electrónico, se elegirá el algoritmo con el que se desea
que creen las claves y posteriormente se cifre la clave de sesión, el tamaño de las claves
y la fecha de expiración, en caso de que queramos que expire. Los métodos de cifrado
más importantes entre los que se pude elegir son RSA y DH/DSS, RSA fue el primer
sistema, al que luego se agregó otra alternativa denominada DH/DSS. Los que todavía
tienen programas PGP antiguos solo pueden utilizar las RSA, por lo que las otras son
menos "universales". Posteriormente es necesario introducir una frase de seguridad que
quedará asociada a la clave privada y será necesario introducir cada vez que usemos la
clave privada.
Partiendo de los datos introducidos y de otras variables aleatorias el programa
generará la pareja de claves con el algoritmo seleccionado, y la huella dactilar
correspondiente, una especie de resumen de la clave pública. El programa pedirá que
mientras se generan las claves se vaya tecleando algo o moviendo el ratón para obtener
más información aleatoria. Es conveniente, porque eso hará que la pareja de claves sea
más distinta a cualquier otra existente.
Hay otras claves, llamadas claves de sesión, las cuales son generadas
aleatoriamente cada vez que se manda un mensaje, y con la cual se cifrará ese mensaje.
La frase de paso o “passphrase”, es como una clave más larga, y en teoría, más
segura. Típicamente está compuesta de múltiples palabras, la frase de paso es más
segura en contra de ataques de diccionario, en los cuales los atacantes prueban con todas
las palabras del diccionario para intentar averiguar la contraseña. Las mejores frases de
paso son relativamente largas y complejas y contienen una combinación de mayúsculas,
minúsculas, números y signos de puntuación.
- 39 -
PGP
PGP utiliza la frase de paso para cifrar la clave privada almacenada en el
ordenador. Más concretamente se usa una función hash de la frase de paso para cifrarla.
Es necesaria la frase de paso para descifrar y usar la clave privada. La frase de paso
debe ser algo fácil de recordar para el usuario y difícil de averiguar por los demás, pues
si un usuario olvida su frase de paso su clave privada es totalmente inútil.
Las claves pueden ser vistas y manejadas a través de una única ventana llamada
“PGPKeys”, en la que también podremos ir añadiendo posteriormente las claves
públicas de otras personas.
Un usuario puede tener más de un par de claves. Cada par puede estar asociado a
varias direcciones de correo electrónico, y la misma dirección de correo electrónico
puede tener varios pares asociados.
Es muy importante no perder las claves. Con la pública no hay mucho peligro
puesto que seguramente la has puesto en algún servidor y también la tienen tus amigos,
lo que te permitirá recuperarla si pierdes tus archivos. Pero la privada solo la tienes tú.
Si la pierdes eso inutilizaría tu pareja de claves. Es muy conveniente hacer una copia de
seguridad de tu clave privada (o de las dos), lo cual consiste en copiar los archivos
pubring.pkr y secring.skr, pero hay que tener prudencia con donde se guardan, sobre
todo el archivo de claves privadas. Ya se ha comentado que al generar la pareja de
claves intervienen ciertos factores aleatorios que son imposibles de controlar. Por lo
tanto es imposible reproducir las claves intentando generarlas de nuevo; eso no
funcionará aunque uses el mismo ordenador con el mismo software y con los mismos
parámetros, obtendrás otras dos claves distintas. Esta característica de "imposible
repetición" es una de las que dan seguridad al sistema. Los especialistas han calculado
que si el más potente ordenador se dedicase exclusivamente a generar claves, tardaría
cientos de años en obtener una pareja de claves igual a la que ya tienes.
No es recomendable compartir la clave privada con otra persona, pero a veces es
necesario. Las clave de firma corporativas, por ejemplo, son claves privadas usadas por
una compañía para firmar. En este caso la clave será conocida por múltiples miembros
de la compañía, lo cual significa que cualquiera puede actuar en nombre de la compañía.
Para solucionar ese problema se divide la clave entre múltiples personas de tal forma
que si hay pocas partes de la clave, ésta no puede ser usada. Una opción sería dividir la
clave en tres trozos y que fuesen necesarios al menos dos de ellos para poder usarla, o
dividirla en dos y que fuesen necesarios los dos. Si hay una conexión segura a la hora de
reconstruir la clave, no es necesario que todos los que posean una parte estén
físicamente presentes en el momento de la reconstrucción de la clave.
La huella es un resumen de la clave pública, se suele incluir en los mensajes de
correo electrónico y por lo tanto puede ser utilizada para comprobar que la clave
obtenida por otros medios coincide con esa huella indicada en el mensaje de correo. La
huella, que no es más que un conjunto de caracteres hexadecimales característicos de la
clave. La huella es algo del tipo "EA10 F561...". La huella se puede convertir en un
conjunto de palabras. Esto es un añadido para facilitar su lectura por teléfono. Muchas
veces, dos personas que deseen intercambiar claves se limitan a darse mutuamente sus
"huellas" en lugar de la clave entera. Puede por ejemplo incluirse en la tarjeta de visita.
- 40 -
PGP
Es posible generar una pareja de claves que no esté asociada a ninguna dirección
electrónica. Aunque PGP está orientado a la transmisión de datos por correo Internet,
también es posible utilizar sus posibilidades en otros sentidos.
Aspecto ASCII de una clave pública:
-----BEGIN PGP PUBLIC KEY BLOCK----Version: PGPfreeware 5.5.3i for non-commercial use
<http://www.pgpi.com>
mQCNAzVm2RwAAQEEAL/DN79rhWIz3895L0/FiPkgdXyGXVuRv2SMD9nD7hgkxGCD
WgosKEymkqqjXk/s8SK6vYXNipu+SoTgLVcJ266ryd2V7Gkl5ZIPRXPGeF7Ufbob
LyE96LeDAZUY16yFAL6Grna8koFzAfdhJX5CXNMiHMQFB25IXKarQCE08evfAAUR
tBhQZXBpdG8gR3JpbGxvIDxub0Buby5ubz6JAJUDBRA1ZtkcpqtAITTx698BAfk2
BACZP8yIQsXNiWZ7lbeKNrAGO6lWaJxutu6OlVI/gXRcUw6sSECv6Yj64FvDkU4r
DbSu/TTSKkCPdcT9hf0QHjD2pY1780s9C6jXHmNJFmssVDLJuayAOPpfMOumsdUQ
MX9iWsGJC6JPdQbfDBBSG6lnpHEEf6Ph8dgzRECjC6G8Xw===rhQ/
-----END PGP PUBLIC KEY BLOCK-----
Huella correspondiente: D5DB 274E 2B68 7D73 194C 9BCF 4ABB B158
Fig.18: Ventana PGPKeys
Esta ventana sirve para la administración de claves. Si activamos todas las opciones
del menú View (ver) veremos toda la información que nos da la ventana. Veremos las
siguientes columnas:
•
Keys (claves): se ve un conjunto de líneas con un icono en forma de llave y
un nombre.
•
Validity (validez): nos indica si la clave se considera válida. Una clave
válida se representa con un círculo verde y una no válida por uno gris en
algunas versiones, como en la 6.5.8, y en otras como en la 8.1 (a la cual
pertenece la Fig.16) se representa con una barra de color gris oscuro la
validez y con una barra blanca la no validez.
•
Size (tamaño): indica el tamaño de la clave en bits. Si la clave es de tipo
RSA, con un icono de llave de color gris, aparecerá un solo número, sin
- 41 -
PGP
embargo si es de tipo Diffie-Hellman, con un icono de llave de color marrón,
aparecerán dos, el primero de ellos es el tamaño de la clave del certificado y
el segundo el tamaño de la clave de firma.
•
Description (descripción): nos indica que tenemos ahí. Los mensajes indican
claves públicas (RSA public key o DH/DSS public key), claves caducadas
(Expired RSA public key o Expired DH/DSS public key) y nuestro propio
par de claves (RSA key pair o DH/DSS key pair). Pero al pinchar en el
cuadradito que hay a la izquierda del icono con la llave, aparecerán más
cosas (ID de usuario, firmas exportables y a veces hasta fotografías).
•
Trust (confianza): se refiere al propietario de la clave. Se representa
mediante una barra gris. Si la confianza en esa persona es tota la barra es gris
oscura, si está mitad gris oscuro y mitad gris claro la confianza será
marginal, y si es totalmente de color gris claro es que no tenemos confianza
en el dueño de la clave. En tu clave la barra será gris oscura con franjas
inclinadas, esto indica confianza implícita, ya que la creaste tú.
•
KeyID (identificador de clave): es un conjunto de ocho caracteres
hexadecimales, precedidos por “0x”, y que identifican la clave.
•
ADK (Clave de Descifrado Adicional): como ya se ha explicado
anteriormente la clave pública cifra una clave simétrica, la clave de sesión,
la cual a su vez cifra el mensaje. Una de las cosas que se puede hacer es
cifrar con más de una clave pública, con el objeto de que diversos
destinatarios puedan descifrar el mismo mensaje. La ADK es un sistema por
el que cualquier mensaje se cifra siempre con dos claves: la del destinatario
y una segunda (la ADK) controlada por la empresa o el administrador de red.
Este sistema está diseñado para entornos empresariales, con objeto de que la
empresa pueda tener cierto control sobre los mensajes cifrados por el. Hay
versiones de PGP que no poseen esta opción, una clave con ADK viene
indicada por un círculo rojo, sin ella, el círculo es gris.
•
Creation (creación) y Expiration (caducidad): indican, la fecha de creación
de la clave y la de caducidad. Si la clave no veremos un Never (nunca).
5.2 Exportación e importación de claves públicas. Servidores de claves.
Para que otras personas tengan acceso a tu clave pública puedes subirla a algún
servidor de los dedicados a almacenar claves públicas de cualquier usuario. El programa
facilita la tarea, pues puede conectar directamente con los servidores. Puedes enviar la
clave a varios servidores, pero basta con que la entregues a uno de ellos, esto es porque
los servidores se comunican periódicamente para entregarse unos a otros las novedades
que cada uno haya recogido, de esta forma es muy probable que tras un tiempo tu clave
esté en muchos servidores públicos de claves. Tú seguirás siendo el único que puedas
descifrar los mensajes, porque serás el único que tenga en su poder la clave privada, por
tanto no debes preocuparte de que tu privacidad se vea comprometida por el hecho de
hacer pública tu clave pública.
- 42 -
PGP
Pueden hacerse modificaciones en las claves almacenadas en un servidor, por
ejemplo añadir nuevas firmas de otros usuarios de PGP o revocar una clave. Hay que
tener cuidado porque no es posible borrar una clave de un servidor, y esa información
quedará allí para siempre. Esto es porque si borramos la clave de un servidor, ésta
reaparecerá cuando el servidor se conecte con otros para actualizarse y le comuniquen
que existe esa clave que el no posee, no hay mensajes estandarizados que se puedan
mandar unos servidores a otros para comunicar que una clave ha sido borrada, por lo
tanto no es posible hacerlo de este modo.
La única forma de cancelarla es revocarla (cancelar su validez) pero para hacerlo
necesitarás tu pareja de claves y también tu frase de seguridad. Luego puedes enviar al
servidor la clave pública revocada, de forma que dicha revocación es añadida a la clave
que ya existía en ese almacén. La revocación también se propagará a los otros
servidores y así quedará patente que esa clave ya no es operativa. Posteriormente puedes
generarte otro juego de claves y enviar la nueva pública al servidor. No olvides que para
revocar la clave necesitas tenerla operativa y además necesitas la frase de seguridad.
Si dejas de usar la cuenta de correo a la que está asociada esa clave surge algún
problema. La clave podría seguir funcionando, pero usar la clave teniendo otra dirección
electrónica puede crear mucha desorientación y recelo en los otros usuarios. Además, es
posible que alguna otra persona utilice el servidor de claves para localizar tu dirección
de correo electrónico. Para evitar estas dificultades, tienes dos alternativas. La primera
consiste en revocar la clave y publicar esa revocación para luego generarte una nueva
clave. La segunda alternativa consiste en agregar a la clave la nueva dirección
electrónica y volver a publicar tu clave con este añadido. En principio una clave se
asocia a una sola persona y a una sola dirección, pero es posible añadir más usuarios y/o
más direcciones.
Cuando necesites la clave pública de otra persona igualmente puedes buscarla en
sus páginas web o en cualquier servidor de claves.
Cuando la encuentres ya la puedes añadir a tu anillo de claves públicas. Si la
clave ya estaba en tu anillo no es añadida de nuevo, pero si tenía nuevas firmas o ha
sido modificada se añadirán las modificaciones a la existente. A partir de ese momento
ya podrás enviarle información cifrada y verificar sus firmas digitales. Sin embargo,
PGP seguirá advirtiendo de que esa clave no es segura ("Invalid Key"). Cuando
obtengas una clave y puedas garantizar totalmente que esa clave corresponde a la
persona que aparece como titular, entonces puedes "validar" esa clave recibida y eso se
consigue haciendo tu firma digital sobre ella, así avalas la validez de esa clave, y PGP
dejará de mostrar el aviso de advertencia. Para firmar otra clave necesitarás usar tu frase
de seguridad y, como ya se ha dicho, sólo debes hacer esto sobre aquellas otras claves
que te merezcan confianza respecto a su relación con la persona o entidad
correspondiente.
Las claves públicas de otros usuarios las irás almacenando en tu anillo público.
En el servidor puedes querer mirar también el estado de tu propia clave o mirar
si alguien nuevo ha firmado una clave que ya tienes…, tiene múltiples opciones.
- 43 -
PGP
5.3 Funcionamiento general
5.3.1. Envío de mensajes
El envío de mensajes consiste básicamente de 4 pasos:
1. Firma digital: este primer paso es opcional. Partiendo de un texto normal lo
primero que hace PGP es la creación de una "firma digital", la cual garantiza
tanto la integridad del mensaje como la autenticidad de su origen.
El funcionamiento es el siguiente:
•
•
•
•
Al texto se le aplica un algoritmo hash.
A la frase de paso se le aplica el mismo algoritmo de hash, con esa clave
y mediante un algoritmo simétrico se descifra la clave privada del
remitente.
Se cifra el resultado de la función hash con un algoritmo asimétrico y la
clave privada descifrada.
Ya tenemos la firma digital creada, ésta será añadida al documento
(cifrado o en claro) antes de transmitirlo.
Fig. 19: Funcionamiento firma digital
En la figuras 19, 20, 22 y 23 se usan algoritmos concretos pero se podrían usar cualquiera de los de la familia
correspondiente. En lugar de MD5 se usaría una función de hash, en lugar de RSA un sistema de cifrado asimétrico y en lugar de
IDEA un sistema de cifrado simétrico.
Mensaje firmado mediante PGP:
-----BEGIN PGP SIGNED MESSAGE----La Universidad de Lepe acaba de publicar un estudio en el que se
demuestra que utilizar Windows prolonga la esperanza de vida.
Investigaron la salud y la longevidad de dos millones de
personas.
- 44 -
PGP
La mitad eran europeos que cotidianamente utilizan ordenadores
con el sistema Windows. El otro millón eran africanos que jamás
han usado un ordenador. Los que emplean Windows viven más
años y tienen mejor salud que los otros.
-----BEGIN PGP SIGNATURE----Version: PGPfreeware 5.5.3i for non-commercial use
<http://www.pgpi.com>
iQCVAwUBNWbZpaarQCE08evfAQHL6wQAsNPP+HamC8i9HVmwwOWgXEy8d69Rcsfi
t4U8+321MYBt+A3o4sycE06b8dZJ2KuosjYl1T0KJba/oolyeUVBICEEXwAUK7/D
cUtEzE6Gf8vHfmSn4aE0Ta68RqUYe4aq1lo/yIMbkmxMh5A/7/e9qzN01mwipqQA
Sz0xh5vzlhs=
=fkrF
-----END PGP SIGNATURE-----
Aquí podemos ver que hay una marca que delimita el comienzo del texto
firmado, y luego se añaden otras dos señales para acotar la información cifrada
que lleva la firma digital correspondiente a ese texto. La firma digital no
aumenta de tamaño cuando afecta a una mayor cantidad de información. El texto
de partida podría ser mucho más largo, y sin embargo la firma seguiría siendo
igual de extensa. La firma digital también incorpora información respecto al
momento en que se efectuó la firma.
Es posible sólo usar esta característica de PGP y mandar el texto en claro
junto con la firma, así no tendríamos privacidad, pero si los ventajas que
proporciona la firma digital.
2. Compresión: este paso es automáticamente ejecutado por PGP a no ser que el
usuario no desee hacerlo. Se obtiene una reducción notable del tamaño del
mensaje, sobre todo si es texto. PGP usa un algoritmo compresión. Por defecto,
sólo las partes que van a ser cifradas son comprimidas.
Las dos ventajas fundamentales de utilizar el algoritmo de compresión
son:
o El ahorro en el tiempo de transmisión y espacio de almacenamiento
o Fortalece la seguridad: reducción de patrones y por lo tanto mayor
resistencia al criptoanálisis.
3. Cifrado del mensaje: PGP utiliza un algoritmo simétrico para cifrar,
combinado con uno asimétrico. Se genera una clave de sesión, de forma
aleatoria. Mediante el algoritmo simétrico y esta clave de sesión, se cifra el
mensaje. La clave de sesión se cifra a su vez mediante el algoritmo asimétrico y
la clave pública del receptor, es decir debemos de conocer ésta previamente. El
motivo de no usar el algoritmo asimétrico para todo el mensaje es que no sería
eficiente, especialmente si tiene varios receptores (habría que incluir un mensaje
cifrado completo por receptor, mientras que con el sistema elegido sólo hay que
incluir un cifrado de la clave de sesión por receptor).
Para ver el aspecto que tiene la información cifrada, primero necesitamos
tener un texto de referencia, el documento original de ejemplo:
- 45 -
PGP
La Universidad de Lepe acaba de publicar un estudio en el que se
demuestra que utilizar Windows prolonga la esperanza de vida.
Investigaron la salud y la longevidad de dos millones de
personas. La mitad eran europeos que cotidianamente utilizan
ordenadores con el sistema Windows. El otro millón eran
africanos que jamás han usado un ordenador. Los que emplean
Windows viven más años y tienen mejor salud que los otros.
Ahora veamos el aspecto del mismo texto, pero ya cifrado:
-----BEGIN PGP MESSAGE----Version: PGPfreeware 5.5.3i for non-commercial use
<http://www.pgpi.com>
hQCMA6arQCE08evfAQP8CbOMO5vfadHRJo8kwNnM5HHG7C30dWmNxu5CPA+m+LQY
bJBYFjMQqNK/NPjvkdjqU2mCWPhJa2nSH+X5xuneLfXnXAxzwvjP7w4a/NFILgyo
VDQzMQScheakDWxScApi4pi/CxfFLVKXOPunFHssJLy5ZcHFWlQfABNuRTI/Gzil
ARuCla0XDs32A/wvChx2SYlkZnQySzjYehcsRISHXlzkX5H7LoUSgaHW6xW/4tYx
nN8N3+VBTyZ7Nxa78dEa3AShWRW3F1IvOj+zv8x+l5OwHZsXYotVYl20b2EVUMF5
bzzkQsFBFt/m4T0Ndg/sFThh7uOGxedBSiV4PrdLO6Wbl92XeLIYI1OHnWAeAkqd
GOr5lZj+TfJTvLHdVfK+7WpTa/vgaYp1w3pASGNCdnThFlQMn5VCKSgD8d6u5KNX
Y6l5YRbaXhatqH1io3XLuGzs6M1MskJ/VFCTQLvpxxU74VVkcZ0ebWO/OaX/cDVt
CbnFphtoAUoe70M0AkgHsxZz1wtSviE8Z/4dJOG8x+maNhPTGw8KBHvH/aDy
=uA7n
-----END PGP MESSAGE-----
Se pueden apreciar las características marcas de comienzo y final que son
usadas por PGP para delimitar la información cifrada.
En el caso de un documento muy pequeño como -el expuesto- la
información cifrada ocupa más espacio que el original. En el caso de un
documento grande, el cifrado ocupará algo más que ésta, pero siempre será
menor que el escrito original; cuanto mayor es el texto de partida, mayor es
también el ahorro de bytes que supondrá la transmisión cifrada, porque el cifrado
necesita un tamaño mínimo, pero implica también una especie de compresión.
Es posible que una información sea cifrada para varios destinatarios.
Cualquiera de ellos podrá descifrarla, independientemente de los otros.
Evidentemente, eso también hará que la información cifrada aumente su
volumen.
4. Codificación: firma, compresión y cifrado no generan un fichero de texto
sino binarios. Como la aplicación principal de PGP es el correo, que requiere
caracteres ASCII, PGP puede codificar el documento resultante mediante el
algoritmo BASE64 automáticamente.
Resumen del proceso de compresión y cifrado con la clave pública de destino:
•
•
•
El mensaje en claro se comprime con un algoritmo de compresión.
Se genera aleatoriamente una clave de sesión.
Se cifra el mensaje comprimido con la clave de sesión mediante un algoritmo
simétrico.
- 46 -
PGP
•
•
Se busca la clave pública del destinatario en el anillo de claves públicas, y con
ella, mediante el algoritmo asimétrico se cifra la clave de sesión.
La clave de sesión cifrada se añade al mensaje cifrado.
Fig.20: Proceso de cifrado
Fig. 21: Formato de un mensaje PGP
- 47 -
PGP
5.3.2. Recepción de mensajes
Para la recepción de mensajes PGP simplemente se invierten todos los pasos del
proceso de envío:
1. Paso de ASCII a binario, si el mensaje fue codificado.
2. Si el mensaje está cifrado PGP recupera la clave de sesión, la cual fue cifrada
usando un algoritmo asimétrico con la clave pública del receptor. Por lo tanto el
receptor usará su clave privada para obtener la clave de sesión. Con la clave de
sesión PGP descifra el mensaje usando el algoritmo de descifrado simétrico. El
proceso completo de descifrado es el siguiente:
•
•
•
Con la frase de paso, tras haberle aplicado una función hash, y mediante el
algoritmo simétrico, se descifra la clave privada de destino.
Con la clave privada descifrada y mediante el algoritmo asimétrico, se
descifra la clave de sesión cifrada.
Con la clave de sesión descifrada y mediante el algoritmo simétrico se
descifra el mensaje.
3. Descompresión del mensaje, si estaba comprimido.
Los tres pasos anteriores se ven en la figura 20:
Fig. 22: Proceso de descifrado
4. Si el mensaje fue firmado PGP verifica la firma, la cual fue cifrada con la clave
privada del emisor del mensaje por lo que PGP usará la clave pública de este
usuario. Se extrae el hash del mensaje y PGP lo compara con el que ha
calculado; si los dos encajan la firma es verificada.
- 48 -
PGP
Proceso de comprobación de la firma digital:
• Se busca la clave pública del emisor y con ella y el algoritmo asimétrico se
descifra la firma.
• Se calcula el hash del mensaje, y se compara con el que se ha obtenido al
descifrar la firma:
• Si son iguales la firma es correcta, si no lo son la firma es incorrecta.
Fig. 23: Verificación de la firma digital
- 49 -
PGP
6. EJEMPLO DE USO DE UN SOFTWARE CONCRETO.
A continuación vamos a ver un ejemplo de utilización de PGP. Se ha instalado la
versión 8.1, nos da a escoger entre varios plugins para integrarlo con diferentes clientes
de correo. Nosotros hemos escogido el Outlook.
Lo primero que debemos hacer es crear nuestras claves. Para ello existe un
asistente de creación de claves:
Fig. 24: Asistente de creación de claves(1)
En esta primera pantalla, introduciremos
nuestro nombre y dirección de mail.
Elegiremos el tipo de algoritmo asimétrico
entre uno de los siguientes: DiffieHellman/DSS, RSA y RSA Legacy (se usa
para que sea compatible con versiones
anteriores). Se especifica también el tamaño
de la clave, que podrá ser entre 1024 y 4096
bits. Por último podremos decidir si
queremos que nuestra clave dure para
siempre o tenga una fecha de expiración
determinada.
En esta pantalla se escoge la frase de paso
que protegerá la clave privada del usuario.
Fig. 25: Asistente de creación de claves(2)
Aquí ya tenemos nuestro par de claves
creado.
Fig. 26: Asistente de creación de claves(3)
- 50 -
PGP
Ahora en la utilidad PGPKeys vemos nuestra clave recién creada. Vemos que
está validada por nosotros mismos, ya que está firmada con la propia clave privada, las
versiones actuales de PGP ya hacen esto por si mismas.
En la pantalla de Certificate Properties se puede ver la propia firma sobre esta
clave, de la misma forma se podría ver cualquier otra firma realizada sobre una clave.
En la pantalla KeyProperties (la que aparece a la izquierda) se pueden ver las
propiedades de la clave, nos da la opción de cambiar la frase de paso, aparece la huella
digital, que la podemos ver en hexadecimal o mediante una serie de palabras y también
se puede ver la validez de la clave y la confianza que tenemos depositada en su
propietario (que en este caso es implícita ya que se trata de nuestra propia clave).
Fig.27: Ventana PGPKeys tras creación de claves
Una vez importada una clave pública deberemos validarla firmándola. Para ello
seleccionamos la clave y con el botón derecho del ratón escogemos “Sign…”. La
pantalla que nos aparece es la siguiente:
- 51 -
PGP
Fig. 28: Ventana para validar una clave
Como la propia ventana nos advierte, firmando una clave se está certificando
que se tiene un conocimiento directo sobre el hecho de que la clave pertenece realmente
al identificador asociado, por lo tanto debemos asegurarnos bien de eso antes de firmar.
Para poder firmar nos solicita la frase de paso ya que la firma se realiza usando
la clave privada. Todas las operaciones que conllevan el uso de la clave privada
necesitan ser autorizadas con la frase de paso ya que la clave privada se encuentra
cifrada basándose en dicha frase de paso.
Fig. 29: Ventana de solicitud de frase de paso
Una vez realizados estos pasos, ya podremos enviar un correo, vamos a ver
como se realizaría.
Fig. 30: Ventana de envío de mensaje
Usaremos los dos botones que proporciona el plugin de PGP para Outlook para
cifrar y firmar el mensaje (los que aparecen marcados en naranja en la parte superior
derecha de la ventana). Para cifrar se usará la clave pública correspondiente a la
dirección destino del mensaje si se encuentra en el anillo público. Para firmar se nos
solicitará nuestra frase de paso ya que se necesita nuestra clave privada para ello.
Ahora el receptor procede a recibir el mensaje, para ello se le solicitará la frase
de paso porque descifrará el mensaje con su clave privada.
- 52 -
PGP
Fig. 31: Ventana de recepción de mensaje
Además de descifrar se comprobará la firma (si se hizo), en caso de no disponer
de la clave pública del emisor del mensaje en el anillo de claves no se podrá verificar la
firma digital. Aquí vemos el resultado de verificar la firma y descifrar el mensaje:
Fig. 32: Mensaje verificado y descifrado
- 53 -
PGP
A continuación vemos las posibilidades que nos ofrece el programa en si, en la
versión 8.1:
Fig. 33: Menú PGPmail
Significado de los iconos:
1. Abre el menu PGPkeys.
2. Cifrar un fichero.
3. Firmar un fichero.
4. Cifrar y firmar un fichero.
5. Descifrar y verificar un fichero.
6. Wipe: borrado seguro de ficheros.
7. Freespace wipe: eliminar datos en todas las zonas libres del disco.
- 54 -
PGP
7. PROBLEMAS Y VULNERABILIDADES DE PGP
Ningún sistema de seguridad de datos es impenetrable. PGP puede burlarse de
diversas maneras. Los posibles puntos vulnerables que hay que tener en cuenta son,
entre otros, el compromiso de la contraseña o de la clave secreta, la manipulación de las
claves públicas, los ficheros que se han borrado pero que siguen todavía en el disco, los
virus y caballos de Troya, los fallos en la seguridad física, las emisiones
electromagnéticas, la exposición en sistemas multiusuario, el análisis de tráfico, y quizá
incluso el criptoanálisis directo. A continuación vamos a ver algunos de los fallos de
mayor relevancia detectados en PGP, y algunos de los problemas y vulnerabilidades que
el sistema tiene.
Algunos fallos de relevancia en PGP son los siguientes:
•
Bug aleatorio 5.0i: un fallo en una sola línea de programación hizo que el
generador de datos aleatorios de PGP 5.0i (versión para Linux) leyese de forma
errónea. Como resultado, las claves usadas podrían ser averiguadas sin mucha
dificultad.
•
Fallos menores. Hay un bug en PGP 6.0.1 por el cual el cifrado de su
componente PGPdisk es más débil de lo que debería ser (la clave usada, en
teoría de 128 bits, es en la práctica más débil). Otro elemento en la versión 5.5.3i
hacía que el borrado seguro (Wipe) no fuese realmente seguro. Ambos fallos
fueron fácilmente corregidos en versiones posteriores.
•
ADK bug: Ralph Senderek descubrió en Agosto de 2000 un fallo asociado a la
llamada clave de descifrado adicional, ADK, ya mencionada. Un nuevo formato
de clave, incorrectamente diseñado, permitía incorporar a escondidas una clave
ADK sin que la alteración fuese detectada. Este bug, grave desde el punto de
vista de la seguridad, aparecía en las versiones 5.5.x a la 6.5.3. Tras estudios de
las claves existentes en los servidores, parece ser que dicho bug nunca ha sido
aprovechado por un atacante. El bug fue corregido en la versión 6.5.8.
•
Ataque checo (o ICZ): en Marzo de 2000, los investigadores checos Vladimir
Klima y Tomas Rosa, publicaron un nuevo ataque no solamente contra PGP,
sino también contra su estándar abierto OpenPGP. Este ya no era solamente un
fallo de programación, sino un serio ataque criptográfico. Resulta muy
interesante en teoría, pero en la práctica requiere acceso físico al ordenador de la
persona atacada, y en ese caso sería más fácil obtener la clave mediante un
troyano. Si se siguen las recomendaciones habituales sobre protección de las
claves privadas, este ataque no es factible. Este ataque no funciona con versiones
posteriores a la 7.0.
•
Armadura ASCII: descubierto en Abril de 2001, permite ocultar un fichero
malicioso (un troyano, o una librería dinámica DLL) en un archivo "recubierto"
con armadura ASCII. A pesar de la gravedad potencial del bug, hay que ser
justo: este fallo no es de PGP en sí, sino del sistema operativo bajo el que opera
(Windows). Esto nos recuerda algo muy importante: la seguridad global de una
cadena es solamente la del eslabón más débil. Hay parche para las versiones
- 55 -
PGP
7.0.3 y 7.0.4; los usuarios de versiones anteriores para Windows pueden
protegerse mediante el uso de elementos de seguridad adicional (cortafuegos y
antivirus).
•
Ataque de Otterloo: en septiembre de 2001, Sieuwert van Otterloo mostró un
fallo que permite "jugar" con la validez de una clave. En claves con más de un
identificador, y bajo ciertas circunstancias, un usuario puede ser engañado a
pensar que una clave es válida cuando realmente no lo es.
Problemas:
•
•
Muchas veces sucede que el mensaje es auténtico pero la firma digital no
puede ser comprobada satisfactoriamente por problemas técnicos. Los
caracteres especiales (acentos, eñes, etc.), los sistemas de codificación del
mensaje y los diferentes programas de correo pueden rechazar la firma
digital, de forma que parezca un mensaje falso sin que realmente lo sea.
El uso de PGP impone ciertas exigencias o limitaciones incómodas. Por
ejemplo, sin PGP puedes configurar tu sistema de correo para que transmita
párrafos verdaderos (líneas tan largas como quieras, que luego son
recompuestas en la pantalla del receptor, para facilitar su visualización). PGP
no funciona bien con este sistema, y exige líneas de un tamaño máximo
(normalmente, menos de 80 caracteres). El usuario no tiene que preocuparse
de hacer las líneas cortas porque el PGP se encarga de "fragmentarlas"
automáticamente. Pero al final esto genera nuevos problemas. Por ejemplo,
si yo quiero poner una URL de 96 caracteres como
...
http://www.mcafee-at-home.com/international/spain/products/pgp-personalsec
u
rity/default.asp?M=6
... sucede que esa URL quedará rota en dos líneas y el receptor que "pinche"
en esa dirección no podrá acceder a la página que yo estaba queriendo
sugerirle; se hace necesario recomponer las dos líneas e introducir el
resultado en el navegador, manualmente.
Vulnerabilidades:
•
Vulnerabilidad de la validez de claves: una clave PGP puede tener más de un
identificador de usuario y más de una dirección de correo electrónico. Es
posible que un atacante añada un identificador falso a una clave pública
legítima. Aunque ese identificador de usuario no está firmado como
propietario de la clave, la clave aparecerá como válida porque el dueño ha
firmado por lo menos uno de los identificadores. Otro usuario puede añadir
la clave a su anillo público y firmarla, posteriormente puede mandar un
mensaje a la dirección falsa, con lo que llegará al atacante. El atacante no
puede descifrar el mensaje, pero el usuario verdadero no puede recibirlo. De
esta forma el atacante utiliza esta vulnerabilidad para romper una
comunicación segura entre dos usuarios de PGP. Protegerse contra esta
vulnerabilidad es fácil, siempre que comprobemos, que en una clave están
- 56 -
PGP
firmados todos los identificadores. Esta vulnerabilidad muestra la
importancia de la ‘self-signature’.
- 57 -
PGP
8. OTRAS APLICACIONES DE PGP
8.1 Cifrado para asegurar tus propios documentos.
Se puede usar el programa PGP para cifrar cualquier fichero, ya sea cifrándolo,
firmándolo digitalmente, o ambas operaciones conjuntas. Si cifras el fichero deberás
usar la clave pública de la persona a la que va dirigido. El fichero cifrado puede ser
transportado en disquete, transmitido a un servidor de FTP, adjuntado a un mensaje de
correo (el mensaje puede ir cifrado o sin cifrar) o por cualquier otro medio. Esto permite
cifrar cualquier clase de fichero, vale igual para un texto que para una imagen, un
archivo de sonido, un ejecutable o un fichero comprimido. El programa no destruye el
fichero original (salvo que se le indique expresamente), generando otro archivo
diferente. Este nuevo archivo tendrá el mismo nombre, pero añadiendo una nueva
extensión -la vieja extensión pasará a formar parte del nombre-; para los archivos
cifrados (con o sin firma) se usará normalmente la extensión PGP, y para los archivos
que solo incorporen firma digital se usará preferentemente la extensión SIG.
Si el fichero está cifrado (con o sin firma), el receptor podrá igualmente usar su
programa PGP para descifrarlo y recuperar una copia del fichero original. Las versiones
más modernas de PGP permiten hacer esto activando directamente el archivo (PGP ya
sabe lo que debe hacer con él, pues lo deduce de la extensión).
Si se aplica a un fichero solamente la opción de la firma, el nuevo fichero
generado tendrá la extensión SIG, pero lo habitual es que solo incluya la información de
la firma digital, haciendo necesaria la transmisión también del fichero original.
Careciendo de este último, el fichero de firma no sirve para nada. Esto puede parecer
una anomalía, pero es una gran ventaja puesto que el fichero fuente queda inalterado y
eso es especialmente conveniente cuando no se trata de texto puro (archivos de
imágenes, ejecutables, etc.). De todas formas hay una opción para indicar a PGP que
incluya en el fichero de firma también la información original, con lo que se puede
transmitir, o conservar, solamente este fichero de firma; solamente con ese archivo
puede hacerse la comprobación de firma y también recuperar el fichero original.
También se puede cifrar un fichero que no se va a enviar a nadie, si se quiere
ocultar su contenido de la vista de otras personas que accedan al ordenador, para ello
bastará con cifrar el archivo considerándote a ti mismo como destinatario, y eso será
suficiente para que solo tú puedas descifrarlo usando tu clave privada y tu frase de
seguridad. Ten en cuenta que el programa, por omisión, no borra el fichero original,
solo crea una copia cifrada, por lo que deberías responsabilizarte de eliminar
correctamente el archivo sin cifrar: cualquiera que entienda el funcionamiento de un
disco informático sabe que es posible recuperar un archivo borrado, incluso si no está en
la papelera. PGP incluye una opción que te permite hacer un "borrado destructivo", la
cual se explicará más tarde, de forma que sea imposible recuperar la información.
Cuando cifras un fichero, la ventana de PGP te mostrará una opción que también te
permite automatizar el borrado destructivo del fichero original, haciendo todo eso como
si fuese una sola operación. Al descifrar siempre se recrea (recupera) el archivo que
generó la copia cifrada y que luego fue eliminado.
- 58 -
PGP
Los archivos no son codificados utilizando el mismo planteamiento que los
textos abiertos. Los ficheros se cifran y/o firman usando un procedimiento de resultados
menos visible y generan un fichero completamente distinto y totalmente ininteligible
que lleva la extensión PGP o SIG. Estos archivos no se restringen a los caracteres
legibles y no respetan los cambios de línea. Por lo tanto, el contenido de un fichero
cifrado/firmado siempre es inutilizable e incomprensible, incluso cuando se trate de un
fichero que originalmente era texto y al que solo se le ha aplicado la firma digital, en
estos casos de ficheros cifrados y/o firmados (PGP o SIG) siempre se hace necesaria la
recuperación del archivo original usando el proceso de descifrado de PGP.
En relación con lo anterior, PGP también permite una alternativa que genera el
fichero cifrado con contenido de tipo texto, en estos casos se emplea la extensión ASC
(abreviatura de ASCII), y el resultado es relativamente similar al de los mensajes de
correo, pero con alguna peculiaridad. La más destacable es que en los ficheros de firma
digital no puede visualizarse directamente el contenido original, ni siquiera cuando la
información cifrada sea texto puro y se ha incluido expresamente en el fichero de firma.
Estos ficheros de extensión ASC también pueden activarse directamente para que sean
procesados automáticamente por PGP.
De todo lo anterior puede deducirse otra consecuencia, si recibes un mensaje
cifrado con firma digital, necesitarás la clave pública del remitente para verificar la
autenticidad, pero careciendo de ella igualmente puedes fiarte del contenido, leer la
información y seguir adelante, el documento es igualmente comprensible y puedes
usarlo prescindiendo de las marcas añadidas por PGP. Sin embargo, con los ficheros
que fueron firmados (extensión SIG o ASC) nunca es posible esta utilización directa y
confiada.
8.2 Uso de PGP para borrar archivos del disco
Cuando se borra un archivo, los datos que éste contiene no son realmente borrados del
disco. Aunque no se vea el nombre al listar los contenidos del disco este se puede
recuperar de forma fácil. Cuando borras un fichero, lo único que estás haciendo es
borrar el enlace al fichero de índices del disco. Es como si tienes un catálogo de libros
en una biblioteca, tú puedes borrar un libro del catálogo, pero seguirás estando en la
biblioteca, aunque te será más difícil de encontrar. Cuando borras un fichero es como si
borrases el libro del catálogo, el fichero seguirá estando allí, aunque para ti no sea fácil
de encontrar. Para borrar completamente un fichero tienes que borrar esa parte del
disco, y esto es lo que la función ‘Wipe’ (borrar) de PGP hace. La función ‘Wipe’ se
basa en el método DoD 5220-22.M, el cual permite una reescritura segura de los datos
mediante un número de pasadas configurable desde las opciones de PGP (por defecto 3,
y eso es mucho más que suficiente).
Hay otros usos de PGP a los que sólo haremos referencia, sin explicarlos a
fondo, como son la creación de redes privadas virtuales y los discos virtuales cifrados.
- 59 -
PGP
9. S/MIME, PGP/MIME
9.1. S/MIME
S/MIME (Secure / Multipurpose Internet Mail Extensions, Extensiones de
Correo de Internet de Propósitos Múltiples / Seguro) es un estándar para criptografía de
clave pública y firmado de correo electrónico encapsulado en MIME.
S/MIME fue creado en 1995 por un grupo de vendedores de software para
prevenir la interceptación y falsificación de mail. Fue construido en el protocolo MIME
estándar existente y de forma que fuese fácil de integrar con los productos de e-mail
existentes. Como está basado en unos estándares soportados de forma general, fue
implementado para una gran variedad de sistemas operativos y clientes e correo.
S/MIME provee los siguientes servicios de seguridad criptográfica para aplicaciones
de mensajería electrónica:
•
•
Autenticación, Integridad y No Repudio: mediante el uso de firma digital.
Privacidad y Seguridad de los datos: mediante el uso de cifrado.
La funcionalidad S/MIME está construida en la mayoría de los clientes de correo
electrónico modernos y son capaces de interoperar entre ellos.
Antes de que S/MIME pueda usarse en alguna de las aplicaciones antes
mencionadas, se debe obtener e instalar una clave/certificado individual de un
Autoridad Certificadora. Esta es la diferencia fundamental con PGP, para el cual no es
necesario obtener el certificado por parte de una Autoridad Certificadora, sino que los
certificados se los firman unos usuarios a otros, para asegurar su validez. Es decir
S/MIME funciona mediante Autoridades Certificadoras centralizadas y PGP mediante
una red de confianza.
9.2. PGP/MIME
PGP/MIME toma como base PGP. Se trata de una integración de PGP con
MIME propuesta por Michael Elkins. PGP/MIME está pasado de moda, no porque sea
malo o débil, sino porque no está estandarizado. Fue especificado en el RFC 2015 en
1996 y reformado en el RFC 3156 el en 2001.
Las ventajas que proporcionaba con respecto a PGP/inline eran:
•
•
•
Los archivos adjuntos eran cifrados y firmados.
Caracteres no ASCII podían ser usados.
La firma PGP estaba separada del cuerpo del mensaje, es un archivo
adjunto
La idea no tuvo mucho éxito, muchos de los clientes de correo no lo soportaban.
- 60 -
PGP
10. REFERENCIAS
Javier González (1999): “Todo sobre PGP”
http://www.geocities.com/siliconvalley/pines/2332/
Página de PGP internacional:
http://www.pgpi.org/
Del capítulo 1 del libro “Introducción a la criptografía” de la documentación de PGP
6.5.1: “How PGP Works”
http://www.pgpi.org/doc/pgpintro/
Phil Zimmermann, traducido por Luis J. Claros Martin: “¿Por qué necesitas PGP?
http://www.pgpi.org/doc/whypgp/es/
Death Master (2005): “Taller de criptografía”
http://www.death-master.tk/
Cristina López Bravo (2006): transparencias del curso 2006-2007 de la asignatura
Redes y Servicios de Comunicaciones II del Departamento de Ingeniería Telemática de
la Universidad de Vigo
http://www-gris.det.uvigo.es/wiki/pub/Main/PaginaRsc2/Clase6-SPT.pdf
David E. Ross (2007): “Pretty Good Privacy (PGP)”
http://www.rossde.com/PGP/index.html#overview
Adam Back: “PGP Timeline”
http://www.cypherspace.org/adam/timeline/
Traducción del anterior por Arturo Quitantes Sierra: “Historia de PGP”
http://www.cripto.es/expedien/exped002.htm
David Hamilton: “PGP for Absolute Beginners”
http://axion.physics.ubc.ca/pgp-begin.html
Kevin Henry: “Getting Started With PGP”
http://www.acm.org/crossroads/xrds6-5/pgptutorial.html
“Secure Mail Communication with PGP”
http://www.trustprofessionals.com/edu/pgp.html
Arturo Quirantes Sierra: “Taller de criptografía”
http://www.cripto.es/
Arturo Quitantes Sierra (2000): “Introducción a PGP”
http://www.cripto.es/pgp01.htm
Arturo Quirantes Sierra (2001): “Curso Sencillo de PGP”
http://www.cripto.es/cursopgp.htm
Páginas de PGP en la Comunidad RedIRIS
http://www.rediris.es/pgp/
- 61 -
PGP
Antonio Caravantes (2006): “Seguridad en el correo electrónico y PGP”
http://www.caravantes.com/pgp/pgp.htm
PGPCorporation
http://www.pgp.com
“PGP”
http://www.orion.cl/partners/?id=02
Tom McCune’s: “PGP Questions & Answers”
http://www.orion.cl/partners/?id=02
Bernard Jonh Poole: “PGP 6.5.8”
http://www.pitt.edu/~poole/PGP.htm
Servicio de Informática y Comunicaciones de la Universidad de Zaragoza: “Seguridad
en el correo.PGP”
http://www.unizar.es/sicuz/correo/mail_pgp.html?menu=correo#referencias
“History of PGP” (1999)
http://openpgp.vie-privee.org/history.htm
Michael W. Lucas (2006): “The story of PGP”
http://www.webmonkey.com/webmonkey/06/17/index4a.html?tw=backend
“Criptografía”
http://www.miginside.com/hck/?q=node/14
Wikipedia en español:
http://es.wikipedia.org/
Wikipedia en inglés:
http://en.wikipedia.org
PGP Global Directory
http://keyserver.pgp.com/
Brenno J.S.A.A.F. de Winter (versión en inglés), Horacio (versión en español):``GNU
Privacy Guard'' (GnuPG) Mini Como
http://webber.dewinter.com/gnupg_howto/spanish/index.html
Secure e-mail clients with PGP
http://www.bretschneidernet.de/tips/secmua.html
PGP, PGP/MIME, OpenPGP, and S/MIME: A Short History (2000)
http://www.uic.edu/depts/accc/newsletter/adn26/history.html
- 62 -
PGP
11. ÍNDICE DE FIGURAS Y TABLAS
Fig. 1: Cifrado simétrico………………………………………………………………12
Fig. 2: Cifrado asimétrico……………………………………………………………..14
Fig. 3: Cifrado de un mensaje en un sistema híbrido………………………………….15
Fig. 4: Descifrado de un mensaje en un sistema híbrido………………………………15
Fig. 5: Mensaje cifrado para dos destinatarios diferentes……………………………..16
Tabla 1: Tiempos de cifrado (en milisegundos en una Sparc II)……………………....20
Tabla 2: Tiempos firmado digital (en milisegundos en un Pentium Pro 200 MHz)…...20
Fig. 6: Una ronda del cifrado IDEA……………………………………………………21
Fig. 7: Esquema funcionamiento Triple-DES………………………………………….22
Fig.8: Tres rondas cifrado CAST-128………………………………………………….23
Fig.9: Etapas cifrado AES……………………………………………………………...24
Fig.10: Funcionamiento TwoFish……………………………………………………....25
Fig. 11: Proceso de firma……………………………………………………………….30
Fig. 12: Proceso de verificación de la firma digital…………………………………….30
Fig.13: Anatomía de un certificado…………………………………………………….32
Fig. 14: Un certificado PGP……………………………………………………………33
Fig. 15: Un certificado X.509…………………………………………………………..34
Fig. 16: Confianza directa……………………………………………………………...35
Fig. 17: Jerarquía de confianza………………………………………………………....35
Tabla 3: Estructura del anillo de claves privadas………………………………………37
Tablas 4 y 5: Estructura del anillo de claves públicas……………………………….…38
Fig.18: Ventana PGPKeys……………………………………………………………..41
Fig. 19: Funcionamiento firma digital…………………………………………………44
Fig.20: Proceso de cifrado……………………………………………………………..47
Fig. 21: Formato de un mensaje PGP………………………………………………….47
Fig. 22: Proceso de descifrado…………………………………………………………48
Fig. 23: Verificación de la firma digital………………………………………………..49
Fig. 24: Asistente de creación de claves(1)…………………………………………....50
Fig. 25: Asistente de creación de claves(2)……………………………………………50
Fig. 26: Asistente de creación de claves(3)……………………………………………50
Fig.27: Ventana PGPKeys tras creación de claves…………………………………….51
Fig. 28: Ventana para validar una clave……………………………………………….51
Fig. 29: Ventana de solicitud de frase de paso………………………………………...52
Fig. 30: Ventana de envío de mensaje……………………………………………........52
Fig. 31: Ventana de recepción de mensaje…………………………………………….53
Fig. 32: Mensaje verificado y descifrado……………………………………………...53
Fig. 33: Menú PGPmail………………………………………………………………..54
- 63 -