Un electrón es lanzado con una velocidad de 2

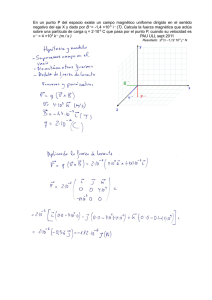
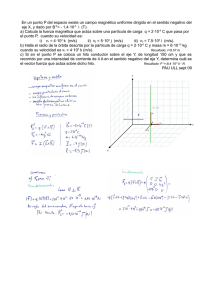
1- Un electrón es lanzado con una velocidad de 2.106 m/s paralelamente a las líneas de un campo
eléctrico uniforme de 5000 V/m. Determinar:
a) La distancia que ha recorrido el electrón cuando su velocidad se ha reducido a 0'5.106 m/s
b) La variación de energía potencial que ha experimentado en ese recorrido.
Solución:
Al tener el electrón carga negativa se ve sometido a una fuerza opuesta al campo
eléctrico que le va frenando:
m.a=q.E
→
a=q.E/m
a = 1'6.10-19 . 5000 / 9'1.10-31 = 8'79.1014 m/s2
Al ser la aceleración constante, las ecuaciones del movimiento son:
v = vo - a . t
→ t = (vo - v) / a = ( 2.106 - 0'5.106 ) / 8'79.1014 = 1'7.10-9 s
e = vo . t - a . t2 /2 = 2.106 . 1'7.10-9 - 8'79.1014 . (1'7.10-9 )2 / 2 = 0'0021 m
La diferencia de potencial entre dos puntos de un campo uniforme es:
VA - VB = E . d = 5000 . 0'0021 = 10'5 Voltios
La variación de energía potencial será:
EpA - EpB = q . (VA - VB ) = - 1'6 . 10-19 . 10'5 = - 1'68.10-18 Julios
2- Dos cargas puntuales e iguales de valor 2 mC cada una, se encuentran situadas en el plano XY en
los puntos (0,5) y (0,-5), respectivamente, estando las distancias expresadas en metros.
a) ¿En qué punto del plano el campo eléctrico es nulo?
b) ¿Cuál es el trabajo necesario para llevar una carga unidad desde el punto (l,O) al punto (-1,0)?
Solución:
La suma de dos
vectores da nulo si
tienen el mismo
modulo y forman entre
sí 180º. En los puntos
situados fuera del
segmento que une las
cargas, segmento AB,
el campo no puede
anularse pues los
campos forman ángulos distintos de 180 º. Sólo puede anularse en el segmento AB.
Como las cargas son iguales, y el campo depende de la distancia del punto a la carga, para que los dos
campos sean iguales y opuestos sólo puede suceder en el punto medio del segmento, en este caso el
origen de coordenadas (0,0). Si se desea comprobar analíticamente, consideremos un punto genérico del
segmento de coordenadas (x,0) y determinemos x para que el campo sea nulo:
Campo creado en P por la carga situada en A:
E = K. q /(5+x)2
Campo creado en P por la carga situada en B:
E = K. q /(5-x)2
Los dos campos deben ser iguales en módulo para que su suma vectorial de campo nulo:
K. q /(5+x)2 = K. q /(5-x)2
→
(5+x)2 = (5-x)2
→
x=0
El trabajo para trasladar una carga de un punto a otro del campo es igual al producto de la carga por la
diferencia de potencial entre los dos puntos; como en este caso la carga es la unidad el trabajo coincide
con la d.d.p.; como el potencial depende de la carga y de la distancia al punto, al ser las cargas iguales y
las posiciones relativas de los puntos, con relación a las cargas, iguales, los potenciales son iguales y por
tanto el trabajo es nulo:
W = q. ( V1 - V2 )
V1 = K. qA / rA + K. qB /rB = 9.109 . 2.10-3 .( 1 /4 + 1 /6) = 7'5.106 Voltios
V2 = K. qA / rA + K. qB /rB = 9.109 . 2.10-3 .( 1 /6 + 1 /4) = 7'5.106 Voltios
V1 - V2 = 7'5.106 - 7'5.106 = 0
→ W = 0 Julios
3- Se tienen tres cargas en los vértices de un triángulo equilátero cuyas coordenadas, expresadas en
cm, son:
A (0,2) , B (-√3, -1) , C (√3, -1)
Se sabe que las cargas situadas en los puntos B y C son iguales a 2 µC y que el campo eléctrico en el
origen de coordenadas (centro del triángulo) es nulo. Determinar:
a) El valor de la carga situada en el vértice A
b) El potencial en el origen de coordenadas
Solución:
El campo eléctrico a una distancia r de una carga es :
E
= [K.Q / r2].u
siendo u el vector unitario en el sentido de la carga al punto
Si
el triángulo es equilátero el centro del mismo equidista de los
vértices, por lo que el valor de r es el mismo para las tres cargas. Al
mismo tiempo los sentidos de los tres campos en el centro del
triángulo forman 120º.
Si
el campo total es nulo, si el centro equidista de los vértices y si los
campos forman 120º, las tres cargas deben ser iguales; por tanto el
valor de la carga situada en el vértice A es de + 2 µC
El potencial en el centro del triángulo será la suma de los potenciales creados por cada carga:
VO = VO,A + VO,B + VO,C
El potencial en un punto debido a una carga es una magnitud escalar de valor:
V = K.Q / r
Al tener cada vértice la misma carga, al tener r el mismo valor para cada carga, se deduce que los
potenciales creados por cada carga son iguales y de valor:
VO,A = VO,B = VO,C = K. Q / r = 9.109 .2.10-6 / 0'02 = 900 000 Voltios
VO = 3 . 900000 = 2 700 000 Voltios
Nota: Con los datos de las coordenadas se puede deducir que el triángulo es equilátero y que el centro del
triángulo coincide con el centro de coordenadas, por lo que estos datos son redundantes.
4- Calcular el campo y el potencial eléctrico producido por un anillo conductor de radio R cargado
con una carga Q, en un punto de su eje perpendicular.
Consideremos un elemento del anillo formado por un arco de apertura dθ . El valor de ese arco será:
dL = R. dθ
y la carga que contiene será:
dq = Q. dL /(2.π.R) = Q. dθ /(2.π)
El campo creado por este elemento de carga en un punto z del eje
perpendicular es:
dE = k. dq / r2 = k. Q. dθ /(2.π. r2)
Este campo puede descomponerse en dos vectores: uno en la dirección del eje z y otro perpendicular al
anterior; esta ultima componente se anulará con la componente producida por un elemento de carga
situado en la posición simétrica en el disco, por lo que sólo interesa la componente en el eje z:
dEz = dE . sen α = [ k. Q. dθ /(2.π. r2) ]. (z / r) = k. Q. z. dθ /(2.π. r3)
El campo total producido por el anillo será la integral respecto a θ entre 0 y 2.π :
Ez = ⌡ dEz = ⌡ k. Q. z. dθ /(2.π. r3) = k. Q. z / r3 = k. Q. z / (z2 + R2)3/2
El potencial creado por el elemento de anillo será:
dVz = k. dq /r = k. Q. dθ /(2.π. r)
El potencial total se obtiene integrando la expresión anterior:
Vz = ⌡ k. Q. dθ /(2.π. r) = k. Q / r = k. Q / (z2 + R2)1/2
5- En tres vértices de un cuadrado de 40 cm de lado se han situado cargas eléctricas de +125 m C.
Determinar el campo eléctrico en el cuarto vértice y el trabajo necesario para trasladar una carga
de - 10 m C desde ese vértice al centro del cuadrado.
El campo producido en D será la suma vectorial de los campos
creados por cada carga:
EC = EA = k.q / a2
EB = k. q / (a2 + a2)
El campo resultante tendrá la dirección y sentido de EB y valdrá:
E = EB + (EA2 + EC2)1/2 = k. q /(2.a2) + (2. k2. q2. / a4)1/2
E = k. q. (1 / 2 + 21/2) / a2 = 9.109. 125.10-6. (1 / 2 + 21/2) / 0'42 =
1'35.107 N /C
El trabajo para trasladar una carga de un punto a otro es la carga por la d.d.p. entre los puntos:
El potencial en un punto es la suma de los potenciales creados por cada carga:
V(D) = k. q / a + k . q. /a + k. q. /(a2 + a2)1/2 = + k. q. (2 + 1 / 21/2) / a
V(D) = 9.109. 125.10-6. (2 + 1 /21/2) / 0'4 = 7613738 Voltios
V(O) = 3. k. q. /( a / 21/2) = 3. 9.109. 125.10-6. 21/2 / 0'4 = 11932427 Voltios
W = q' . (V(O) - V(D)) = - 10.10-6. ( 11932427 - 7613738 ) = 43'2 J
6- Dos cargas de + 12 mC y - 18 mC están separadas 40 cm. Determinar en qué punto del espacio
el campo es nulo.
La suma de dos vectores da nulo si tienen el mismo
modulo y forman entre sí 180º. En los puntos como
B, C y D el campo no puede anularse pues los
campos forman ángulos distintos de 180 º. Sólo
puede anularse en el eje que une las cargas y a
derecha o izquierda de ellas, no entre ellas. En el
punto E no puede ser pues la carga negativa es
mayor y genera un campo todavía mayor por estar
más próxima al punto. La única posibilidad es en un
punto como el A. En A los campos creados por las
cargas son opuestos y valen:
E+q = k. 12.10-6 / x2
E-q = k. 18.10-6 / (0'4 + x)2
Para que el campo total sea nulo los dos campos deben ser iguales en módulo:
k. 12.10-6 / x2 = k. 18.10-6 / (0'4 + x)2
El campo se anula a 1'78 m de la carga positiva.
→
12 / x2 = 18 /(0'4 + x)2
→
x = 1'78 m
7- Dos cargas eléctricas puntuales de +10 m C y - 10 m C están separadas 10 cm. Determinar el
campo y potencial eléctrico en el punto medio de la recta que las une y en un punto equidistante 10
cm de las cargas.
En el punto C los campos creados por cada carga son iguales en módulo,
dirección y sentido, hacia la carga negativa. El campo total será:
E(C,+q) = E(C,-q) = k.q /(a/2)2
E(C) = 2. k.q. 4 / a2 = 8.9.109.10.10-6 /0'12 = 7'2 N /C
El potencial será:
V(C) = k. q / (a/2) + k.(-q) /(a/2) = 0 Voltios
El punto A y las cargas forman un triángulo equilátero. En el punto A, también por igualdad de datos, los
módulos de los campos son iguales y sus sentidos los del dibujo y el campo total será paralelo a la recta
que une las cargas:
E(A,+q) = E(A,-q) = k.q /a2
El valor de E(A) resulta ser igual al campo creado por una carga por ser el triángulo equilátero:
E(A) = [E(A,+q)2 + E(A,-q)2 - 2. E(A,+q). E(A,-q).cos 60]1/2
E(A) = k.q /a2 = 9.109.10.10-6 /0'12 = 9.109 N /C
V(A) = k. q /a + k. (-q) /a = 0 Voltios
8- Dos esferas de 25 gramos están cargadas con idéntica carga eléctrica y cuelgan de dos hilos
inextensibles y sin masa de 80 cm de longitud, suspendidos del mismo punto. Los hilos forman 45º
con la vertical. Calcular la carga de cada esfera y la tensión del hilo.
La fuerza F que separa las cargas se debe a la repulsión electrostática, pues ambas son del mismo signo.
F = k. q2 / x2
x = 2. a. sen (q /2)
Si están en equilibrio la suma de la fuerza electrostática y el peso
debe tener la dirección de la cuerda:
tg (q /2) = F /p
k. q2 / x2 = m.g. tg (q /2)
→
→
F = p. tg (q /2)
q2 = m. g. x2 .tg (q /2) / k
q =2.a.sen (q /2).[ m. g..tg (q /2) / k]1/2 =2. 0'8. sen 45 .[25.10-3.9'8 .tg45 /9.109 ]1/2 = 5'9.10-6 C
F = 9.109 . (5'9.10-6)2 / (2.0'8.sen45)2 = 0'245 N
La tensión del hilo será:
T = R = p / cos(q /2) = 25.10-3 .9'8 / cos45 = 0'35 N
9- Entre dos placas planas existe una diferencia de potencial de 15 V y la intensidad del campo
eléctrico es 30 N /C. Determinar:
a) La separación entre las placas.
b) La aceleración que experimenta una partícula de 5 gramos y carga +2'5.10-9 C situada entre las
placas.
c) La variación de la energía potencial al pasar la partícula de una placa a la otra.
De las definiciones de Intensidad de campo y Diferencia de potencial entre dos puntos se infiere que la
separación d entre las placas es:
d = (V1 - V2) / E = 15 / 30 = 0'5 m
La fuerza que experimenta una partícula cargada situada en el interior del condensador es:
F = q. E = 2'5.10-9 . 30 = 7'5.10-8
y su aceleración será:
a = F / m = 7'5.10-8 / 5.10-3 = 1'5.10-5 m /s2
La variación de energía potencial si la partícula fuera de una placa a la otra sería:
Ep = q.(V1 - V2) = 2'5.10-9 . 15 = 3'75.10-8 Julios
10- Una partícula de 2 gramos con carga eléctrica de + 50 m C lleva una velocidad horizontal de 40
m/s en el instante en que entra entre las armaduras de un condensador, por su eje central. El
condensador plano tiene sus armaduras paralelas a la superficie terrestre, suficientemente extensas,
separadas 10 cm, la superior es la positiva, y sometidas a una d.d.p. de 500 Voltios. Determinar la
trayectoria de la partícula y el punto de impacto con la placa, si lo hubiere.
El
campo eléctrico uniforme que crea el condensador es:
E
= V / d = 500 / 01 = 5000 N /C
Este campo actúa sobre la partícula provocando una
aceleración de valor:
= F / m = q. E / m = 50.10-6 .5000 / 2.10-3 = 126 m /s2
ae
hacia la placa negativa, placa inferior.
Por tanto la partícula se ve sometida a la aceleración de la
gravedad y a la aceleración electrostática, siendo la
aceleración total vertical, hacia abajo, y de valor:
ay = 9'8 + 125 = 134'8 m /s2
Las ecuaciones del movimiento, tomando como origen de tiempos y coordenadas el punto de entrada en
el condensador, serán:
ax = 0
ay = - 134'8
vx = 40
vy = - 134'8. t
x = 40. t
y = - ½. 134'8. t2
ecuaciones que se corresponden a las de un movimiento parabólico, pues la trayectoria es:
y = - ½. 134'8. t2 = - ½. 134'8. (x /40)2 = - 0,042125. x2
Para determinar el punto de impacto con la placa basta imponer la condición y = - 0'05 m
- 0'05 = - 0,042125. x2
→
x = (0'05 /0'042125)1/2 = 1'09 m
Constantes físicas
Constante de gravitación universal
G
Radio de la Tierra
RT
Masa de la Tierra
MT
Radio de la Luna
Masa de la Luna
Velocidad del sonido en el aire
Velocidad de la luz en el vacío
c
Constante de Coulomb
k
Unidad elemental de carga
uec
Constante dieléctrica del vacío
eo
Permeabilidad magnética en el vacío
mo
Constante de Planck
h
Masa del electrón
me
Masa del protón
mp
Masa del neutrón
mn
Constante de Boltzmann
k
Constante de Faraday
F
Constante de Stefan-Boltzmann
s
Número de Avogadro
N
Constante de gases ideales
R
6''67.10-11 N.m2.kg-2
6'37.106 m
5'98.1024 kg
1'74.106 m
7'47.1022 kg
340 m /s
3.108 m/s
9..109 N.m2.C-2
1'6021.10-19 C
8'854.10-12 C2.N-1.m-2
4.p.10-7 T.m.A-1
6'625.10-34 J.s
9'1091.10-31 kg
1'6725.10-27 kg
1'6748.10-27 kg
1'38.10-23 J /k
9'65.104 C
5'67.10-8 W.m-2.K-4
6'025.1023 mol-1
8'314 J /mol .K