proyecto de fisica

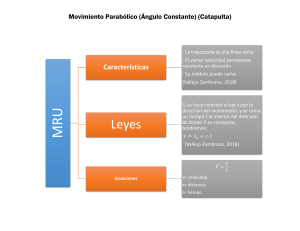
1. Introducción
Hacia finales del siglo XV la sociedad tenía planteados importantes problemas
prácticos: de navegación, tecnológicos, contables... Resolver esos problemas fue
uno de los motores que facilitaron el rápido avance de las matemáticas
renacentistas y posteriores. Uno de estos problemas era el tiro o movimiento
parabólico. La trayectoria de un proyectil, lanzado con una cierta velocidad y un
determinado ángulo de inclinación, se ve afectada por la acción de la gravedad.
Encontrar las leyes matemáticas que rigen el movimiento de los proyectiles fue
una tarea en la que se embarcaron grandes matemáticos, como Tartaglia y
Galileo. En esta aplicación vamos a manejar un pequeño cañón que lanza pelotas
de tenis. Se denomina movimiento parabólico al realizado por un objeto cuya
trayectoria describe una parábola. Se corresponde con la trayectoria ideal de
un proyectil que se mueve en un medio que no ofrece resistencia al avance y que
está sujeto a un campo gravitatorio uniforme.
En realidad, cuando se habla de cuerpos que se mueven en un campo gravitatorio
central (como el de La Tierra), el movimiento es elíptico. En la superficie de la
Tierra, ese movimiento es tan parecido a una parábola que perfectamente
podemos calcular su trayectoria usando la ecuación matemática de una parábola.
La ecuación de una elipse es bastante más compleja. Al lanzar una piedra al aire,
la piedra intenta realizar una elipse en uno de cuyos focos está el centro de la
Tierra. Al realizar esta elipse inmediatamente choca con el suelo y la piedra se
para, pero su trayectoria es en realidad un "trozo" de elipse. Es cierto que ese
"trozo" de elipse es casi idéntico a un "trozo" de parábola. Por ello utilizamos la
ecuación de una parábola y lo llamamos "tiro parabólico". Si nos alejamos de la
superficie de la Tierra sí tendríamos que utilizar una elipse (como en el caso de los
satélites artificiales).
1
2. Objetivos
2.1
General
Como objetivo principal del proyecto es desarrollar e implementar una
simulación que represente el movimiento parabólico de proyectiles. Sea una
manera de enseñar a los estudiantes los diferentes tipos de movimientos.
2.2 Objetivo Especifico

Utilizar el proyecto como instrumento de aprendizaje.

Integrar y Aplicar conocimientos adquiridos a lo largo de la carrera
con el fin de obtener el resultado esperado.

Incrementar conocimientos sobre leyes físicas, de simulación y
programación.

Brindar una nueva herramienta de aprendizaje a los estudiantes que
necesitan conocer el tema.
2
3. Marco teórico
Movimiento parabólico (completo): El movimiento parabólico completo se puede
considerar como la composición de un avance horizontal rectilíneo uniforme y un
lanzamiento vertical hacia arriba, que es un movimiento rectilíneo uniformemente
acelerado hacia abajo (MRUA) por la acción de la gravedad. En condiciones
ideales de resistencia al avance nulo y campo gravitatorio uniforme, lo anterior
implica que:
1. Un cuerpo que se deja caer libremente y otro que es lanzado
horizontalmente desde la misma altura tardan lo mismo en llegar al suelo.
2. La independencia de la masa en la caída libre y el lanzamiento vertical es
igual de válida en los movimientos parabólicos.
3. Un cuerpo lanzado verticalmente hacia arriba y otro parabólicamente
completo que alcance la misma altura tarda lo mismo en caer.
El movimiento parabólico puede ser analizado como la composición de dos
movimientos
rectilíneos:
un movimiento
rectilíneo
uniforme horizontal
y
un movimiento rectilíneo uniformemente acelerado vertical.
El tiro parabólico tiene las siguientes características:

Conociendo la velocidad de salida (inicial), el ángulo de inclinación inicial y
la diferencia de alturas (entre salida y llegada) se conocerá toda la
trayectoria.

Los ángulos de salida y llegada son iguales.

La mayor distancia cubierta o alcance se logra con ángulos de salida de
45º.

Para lograr la mayor distancia fijado el ángulo el factor más importante es la
velocidad.

Se puede analizar el movimiento en vertical independientemente del
horizontal.
3
Cuando un objeto es lanzado con cierta inclinación respecto a la horizontal y bajo
la acción solamente de la fuerza gravitatoria su trayectoria se mantiene en el plano
vertical y es parabólica.
Nótese que estamos solamente tratando el caso particular en que factores como la
resistencia del aire, la rotación de la Tierra, etc., no introducen afectaciones
apreciables. Vamos a considerar también que durante todo el recorrido la
aceleración debido a la gravedad (g) permanece constante y que el movimiento es
sólo de traslación.
Para facilitar el estudio del movimiento de un proyectil, frecuentemente este se
descompone en las direcciones horizontal y vertical. En la dirección horizontal el
movimiento del proyectil es rectilíneo y uniforme ya que en esa dirección la acción
de la gravedad es nula y consecuente, la aceleración también lo es. En la
dirección vertical, sobre el proyectil actúa la fuerza de gravedad que hace que el
movimiento sea rectilíneo uniformemente acelerado, con aceleración constante.
Sea un proyectil lanzado desde un cañón. Si elegimos un sistema de referencia de
modo que la dirección Y sea vertical y positiva hacia arriba:
a y = - g y a x = 0.
Además suponga que el instante t = 0, el proyectil deja de origen (X i = Y i = 0) con
una velocidad Vi.
4
Si Vi hace un ángulo qi con la horizontal, a partir de las definiciones de las
funciones sen y cos se obtiene:
Vxi = Vi cos θ
Vyi = Vi sen θi
Como el movimiento de proyectiles es bidimensional, donde ax = 0 y ay = -g, o sea
con aceleración constante, obtenemos las componentes de la velocidad y las
coordenadas del proyectil en cualquier instante t, con ayuda de las ecuaciones ya
utilizadas para el M.R.U.A. Expresando estas en función de las proyecciones
tenemos:
X = Vxit = Vi cos θi t
y = Vyi t + ½ at2
Vyf = Vyi + at
2ay = Vyf2 - Vyi2
5
Si un proyectil es lanzado horizontalmente desde cierta altura inicial, el movimiento
es semi-parabólico.
Las ecuaciones del movimiento considerando Vyi = 0 serían:
X = Vxi t
y = yo - ½ gt2
Altura máxima que alcanza un proyectil:
Tiempo de vuelo del proyectil:
6
Alcance del proyectil:
Caída Libre: El movimiento de los cuerpos en caída libre (por la acción de su
propio peso) es una forma de rectilíneo uniformemente acelerado.
La distancia recorrida (d) se mide sobre la vertical y corresponde, por tanto, a una
altura que se representa por la letra h.
En el vacío el movimiento de caída es de aceleración constante, siendo dicha
aceleración la misma para todos los cuerpos, independientemente de cuales sean
su forma y su peso. La presencia de aire frena ese movimiento de caída y la
aceleración pasa a depender entonces de la forma del cuerpo. No obstante, para
cuerpos aproximadamente esféricos, la influencia del medio sobre el movimiento
puede despreciarse y tratarse, en una primera aproximación, como si fuera
decaída libre.
La aceleración en los movimientos de caída libre, conocida como aceleración de la
gravedad, se representa por la letra g y toma un valor aproximado de 9,81
m/s2 (algunos usan solo el valor 9,8 o redondean en 10).
Si el movimiento considerado es de descenso o de caída, el valor de g resulta
positivo como corresponde a una auténtica aceleración. Si, por el contrario, es de
ascenso en vertical el valor de g se considera negativo, pues se trata, en tal caso,
de un movimiento decelerado.
Para resolver problemas con movimiento de caída libre utilizamos las siguientes
fórmulas:
7
Para conocer la velocidad final (vf), apliquemos la fórmula
Ahora, para conocer la altura (h) aplicamos la fórmula:
8
4. Materiales y Técnicas Utilizadas
Técnicas Utilizadas.-Para poder llevar a cabo este proyecto lo que se hizo
primero fue en investigar todo lo que era respecto a mi tema como movimiento
parabólico , caída libre , altura máxima. Una vez consultado tuve que investigar el
experimento que esté relacionado con mi tema es decir que conlleve todo lo
investigado y unir en un solo experimento sus cálculos físicos.
Materiales utilizados:





Palos de helado
Cinta
Brujita
Tapa plástica
Ligas
5. Resultados
9
10
6. Conclusión

Por medio de los resultado de la velocidad inicial se puede concluir que para que
un movimiento parabólico se pueda realizar exitosamente, se debe de mantener
un ambiente estable para lograr los resultados que realmente se están buscando,
por lo que la ubicación y el estado de los elementos que se están utilizando entran
a jugar un papel muy importante, y así, de esta forma, podremos obtener el
resultado esperado.

Que las condiciones del ambiente no se toman en cuenta para lograr un resultado
estándar, de lo contrario se dependería de un lugar y un tiempo específico para
lograr "los mismos resultados", lo cual es prácticamente casi imposibles.
11
7. Recomendaciones
Saber de dónde proceden las fórmulas para así poder explicar de una manera
segura nuestro experimento y que mis compañeros puedan entender dicho tema
ya que es un poquito complicado, claro tampoco hay que dejar de lado lo que el
profesor nos diga ya que es para nuestro bien y si él nos dice o nos da alguna
observación nosotros debemos corregirla.
12
8. Web- grafía
http://es.wikipedia.org/wiki/Movimiento_parab%C3%B3lico
http://recursostic.educacion.es/descartes/web/materiales_didacticos/comp_movimi
entos/parabolico.htm
http://www.educaplus.org/play-110-Tiro-parab%C3%B3lico.html
http://www.monografias.com/trabajos98/movimiento-parabolico/movimientoparabolico.shtml
http://genesis.uag.mx/edmedia/material/fisica/movimiento8.htm
recursostic.educacion.es/gauss/web/.../eso/...parabolico/actividad.htm
9. Bibliografía
http://librosgratisparaeluniversitario.blogspot.com/2014/02/fisica-jerry-d-wilsonanthony-j-buffa.html
http://www.cosaslibres.com/search/pdf/fisica-douglas-giancoli
http://www2.ib.edu.ar/becaib/cd-ib/trabajos/Tonzar.pdf
Serway, Raymond A.; Jewett, John W.(2004). Physics for Scientists and Engineers
(6th ed. edición). Brooks/Cole.
Landau y Lifshitz. Física Teórica, Mecánica. Editorial Reverté (1970).Pag.527
13
10. Anexos
14