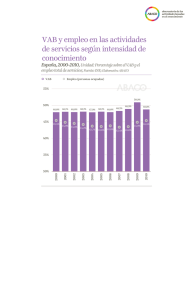
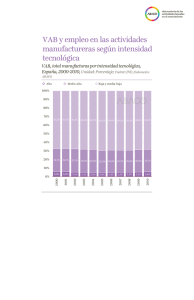
BLOQUE 3-1
Anuncio

BLOQUE 3-3. CIRCUITOS ELÉCTRICOS CON CORRIENTE TRIFÁSICA 1. Circuitos polifásicos. Circuitos trifásicos Circuito polifásico: Un sistema es polifásico cuando en el coexisten varias corrientes monofásicas desfasadas entre sí. Circuito polifásico equilibrado: Un sistema es polifásico equilibrado cuando en el coexisten varias corrientes monofásicas desfasadas entre sí y se dan las siguientes condiciones: 1-Las corrientes alternas monofásicas tienen todas la misma frecuencia y amplitud (y por tanto valor eficaz). 2-Presentan una diferencia entre fases determinada (2π/nºfases) y dichas corrientes están dadas en un orden determinado. La existencia de un sistema equilibrado implica que: a-Los generadores o el generador polifásico producen un sistema de tensiones equilibrado igual al número de fases. b-Los receptores constan de un número igual de fases de idénticas características. Circuito polifásico desequilibrado: Cuando no se cumple alguna de las condiciones anteriores hablamos de sistemas desequilibrados. Sistema de cargas desequilibradas: Es cuando el conjunto de impedancias distintas dan lugar a que por el receptor circulen intensidades de fase diferentes aunque las tensiones del sistema o de la línea sean equilibradas. Sistema trifásico. Un sistema trifásico es aquel formado por tres intensidades de la misma frecuencia. Cuando tienen la misma amplitud y además están desfasadas 120º hablamos de sistema trifásico equilibrado. I 0º 90º 180º 120º ωt 270º 360º 240º Generación de un sistema trifásico de corrientes equilibradas: Cuando una espira gira en el interior de un campo magnético uniforme con velocidad ω constante, sobre ella se induce una fem senoidad. Esto también se produce si lo que permanece fijo es la espira (estátor) y lo que gira es el campo magnético (rotor) que es el caso de los generadores eléctricos. Si el estátor está constituido por tres espiras desfasadas 120º se inducen tres fems alternas senoidales de la misma frecuencia y desfasadas 120º. Secuencia de fases: El orden en que esas tensiones se suceden recibe el nombre de secuencia de fases que puede ser positiva o directa y negativa o inversa. Va = V0 º Va = V0 º Vc Vb = V240 º Vb = V120 º 120º Vc = V120 º Va Vb Secuencia directa Vb 120º Vc = V240 º Va Vc Secuencia inversa NOTA: Según las distintas fuentes bibliográficas a las 3 fases se les designa de tres formas distintas a,b,c 1,2,3 R,S,T 2. Conexiones de fuentes, en estrella y en triángulo. Si las corrientes originadas fuesen independientes, harían falta seis conductores, dos por cada fase. Como esto resulta muy caro, se hacen dos tipos de conexiones que precisan menos conductores, la conexión en estrella y la conexión en triángulo. Conexión en estrella: Se hace uniendo las tres fuentes de tensión a un punto único llamado neutro que se suele conectar a tierra. a’ Va a c Vca Vca Vc N b’ Vb b Vab Vca Vc Vbc N c’ Vc c Vab a Va Vbc Vb Vb Va Vab Vbc b Conexión en triángulo: Se hace uniendo el final de una fuente con el comienzo de la siguiente ºformando un sistema cerrado. c a’ Va b’ a Vb b c’ Vc c Vca Vab Vca Vbc Vab Vca Vbc Vbc Vca Vab Vbc b Vab a 3. Tensiones e intensidades de fase y de línea. Relación entre ellas en sistemas equilibrados. Tensión de fase Vf: Intensidad de fase If: Es la tensión entre un hilo de fase y el neutro. Es la intensidad en un hilo de fase. Son Va,Vb,Vc Son (o V 1,V 2,V 3 , Ia, Ib, Ic (o I 1, I 2, I 3 , o I R , I S , I T ) o Intensidad de línea Il: Es la intensidad que suministra uno de los generadores o que consume uno de los receptores de la carga. Son: V R ,V S ,V T ) Tensión de línea Vl: Es la tensión entre dos fases. Son: V ab = V a − V b I ab V bc = V b − V c Ibc V ca = V c − V a I ca Relación linea-fase en una conexión en estrella: Vca c Il=If=Ic Vc Vab Ic Ic Vca Vc Vbc Va Il=If=Ia Ia Vb N Ib a Il=If=Ib Va Vb Vab Ib b Vbc Ia Si el sistema es equilibrado se verifica que: Si la secuencia es directa: 1.- las tensiones de línea están adelantadas 30º respecto de la tensión de fase. 2.- las tensiones de fase son iguales y desfasadas 120º. Vlinea = 3.V fase I linea = I fase Si la secuencia es inversa las tensiones de línea están retrasadas 30º respecto de la tensión de fase. Vca En el esquema representado anteriormente tendremos entonces que: Va = V fase 0 º Vab = 3.V fase 30 º = Vlinea 30 º Vb = V fase−120 º Vbc = 3.V fase−90 º = Vlinea −90 º Vc = V fase120 º Vca = 3.V fase150 º = Vlinea150 º Vab Vc Va Vb Vbc Relación linea-fase en una conexión en triángulo: c c Ic Ibc Vca Ica Vca Ica Ic Vab Vbc Iab Ib Vl=Vf=Vbc Ibc Ia Vl=Vf=Vca Vl=Vf=Vab b a Iab a Vbc Ia b Ib Si el sistema es equilibrado se verifica que: Vlinea = V fase I linea = 3.I fase Si la secuencia es directa: 1.- las intensidades de línea están adelantadas 30º respecto de la tensión de fase. 2.- las intensidades de línea son iguales y desfasadas 120º. Si la secuencia es inversa las intensidades de línea están retrasadas 30º respecto de la tensión de fase. En el esquema representado anteriormente tendremos entonces que: Ia = I línea−30 º Ia = 3.I fase−30 º Ib = I línea−150 º Ib = 3.I fase−150 º Ic = I línea 90 º Ic = 3.I fase 90 º 4. Conexión de receptores 1.Cargas equilibradas en estrella Esta conexión se hace cuando la tensión nominal de los receptores coincide con la tensión de fase de la red. Se conectan las cargas entre una fase y el neutro a b c Z Z Z N Vc Vbc Vca c Ic Z Ia a Va Z Vab Z b Ib Vb Si las cargas son equilibradas, Za=Zb=Zc=Z ( ) V bc = Vb.( 3 ) = V V ca = Vc.( 3 ) = V V ab = Va. 3 30 = Vlinea 30 º = V a − V b 30 linea − 90 º = Vb − Vc 30 linea150 º = Vc − Va Vca Vab Ic Z Vc Va Ib V a = V fase 0 º Vb V b = V fase −120 º Ia Vbc V c = V fase120 º Ia = V a Z Ib = V b Z Ic = V c Z La intensidad del neutro al ser equilibrado el sistema 2.Cargas desequilibradas en estrella c I n = I a + Ib + I c = 0 Ic Vbc c Vca a Zc Ia N Za Vab b Zb Ic b Va Si las Ia = Va Za cargas son Ib = Vb Zb Vb Vc In equilibradas, Ic = Vc Za ≠ Zb ≠ Zc y como es lógico: Zc Zab La intensidad del neutro al ser desequilibrado el sistema I n = I a + Ib + I c ≠ 0 3.Cargas equilibradas en triángulo Esta conexión se hace cuando la tensión nominal de los receptores coincide con la tensión de línea de la red. a Se conectan las cargas entre dos fases Si el sistema es equilibrado las tres impedancias son iguales. b Zbc Zca c a Ia Vca Vab a Iab Ica Z Z b Ib Ibc Vbc Vc Vb N c Va c Z b Ic -Ibc Si las cargas son equilibradas, Zab=Zbc=Zca=Z Las intensidades de línea son: If = Vf Z = Vl Z Vca Ica Ic Vab ⇒ ⇒ Il = 3.If = 3.Vl Iab Z Ib I a = I línea − 30 º = Iab.( 3 − 30 ) = I ab − I ca Ibc -Ica Ia -Iab Ib = I línea −150 º = Ibc.( 3 − 30 ) = Ibc − I ab Vbc I c = I línea 90 º = Ica.( 3 − 30 ) = I ca − Ibc 2.Cargas desequilibradas en triángulo a a Ia Zab Vca Vab a Iab Ica b Zab Zbc Zca c b Ib b Vbc N Vc Vb Va Zab ≠ Zbc ≠ Zca Entonces Iab = Vab Ibc = Vbc Ibc = Vbc Zab Zbc Zbc I a = I ab − I ca Si las cargas son equilibradas, Ib = Ibc − I ab I c = I ca − Ibc Zca c Zcb Ibc Ic c 5. Equivalencia de receptores estrella-triángulo. Teorema de Kennelly Para convertir un triángulo de cargas en su estrella equivalente se hace de la siguiente manera: Za = Zac.Zab Zab + Zac + Zbc Zab = Za + Zb + Zb = Za.Zb Zc Zab.Zbc Zab + Zac + Zbc Zbc = Zb + Zc + Asociación en estrella Zc = Zb.Zc Za Zbc.Zac Zab + Zac + Zbc Zac = Za + Zc + Za.Zc Zb Asociación en triángulo a a Za Zac c Zc c Zab Zbc b Zb b 6. Potencia en sistemas trifásicos equilibrados Cuando se nos de una tensión y no se diga nada, supondremos que es la de línea (es decir, V=Vl y I=Il). P = 3.Il.Vl. cos ϕ P = 3.If .Vf . cos ϕ Q = 3.If .Vf .senϕ S = 3.Uf .If operando se obtiene que Q = 3.Il.Vl.senϕ S = 3.Il.Vl 7. Corrección del factor de potencia de una instalación trifásica 1. Corriente alterna monofásica Si partimos de una situación 1 y queremos llegar a una situación 2 como las representadas en el dibujo, para la misma potencia P, y siendo QC, la disminución de la componente reactiva establecida al colocar un condensador en paralelo con cada una de las cargas: ⎫ P ⎪ ⎪⎪ Q tgϕ 2 = 2 ⎬ P.(tgϕ1 − tgϕ 2 ) P ⇒ C= ⎪ Q1 = Q2 + QC ⎪ ω.V 2 ⎪⎭ Qc = Q1 − Q2 = P.(tgϕ1 − tgϕ 2 )⎫ ⎬ QC = C.ω.V 2 ⎭ Q tgϕ1 = 1 S2 ϕ1 S2 ϕ2 P Q1 QC Q2 2. En corriente alterna trifásica. En este caso podemos optar por dos configuraciones con los condensadores en estrella o triángulo: Carga trifásica Carga trifásica En triángu lo al ser los tres condensado res iguales en conjunto tienen una potencia reactiva de En estrella al ser los tres condensado res iguales en conjunto tienen una potencia reactiva de Vf 2 = 3.Vf 2 .ω .C Υ y como VL = 3 .V f Xc 2 obtenemos que Qc = VL .ω .C Υ y operando como Qc = 3. en el caso de la corriente monofásica obtenemos que para cada condensado r : P.(tg ϕ1 − tg ϕ 2 ) CΥ = ω .Vl 2 Vl 2 = 3 .Vl 2 .ω .C ∆ y operando como Xc en el caso de la corriente monofásica obtenemos que para cada condensado r : Qc = 3 . P.(tg ϕ1 − tg ϕ 2 ) 3.ω .Vl 2 Por tanto C ∆ = C Υ /3 y siempre se usarán en ∆ C∆ = 8. Cuadro resumen de los sistemas trifásicos equilibrados Estrella Triángulo Estrella y triángulo Tensión fase de Vf = Vl / 3 Vf=Vl Sf Tensión línea de Vl = Vf . 3 Vl=Vf S Intensidad de fase If=Il If = Il / 3 P P = 3.Pf = 3.Vf .If . cos ϕ = 3.Vl.Il. cos ϕ W Intensidad de línea Il=If Il = If . 3 Q Q = 3.Qf = 3.Vf .If .senϕ = 3.Vl .Il.senϕ VAr Sf=Vf.If S = V .I * S = S = 3.Sf = 3.Vf .If = 3.Vl.Il S = P2 + Q2 P = S . cos ϕ = S 2 − Q 2 Q = S .senϕ = S 2 − P 2 Estrella (secuencia directa) Triángulo(secuencia directa) V ab = V a − V b I a = I ab − I ca V bc = V b − V c Ib = Ibc − I ab V ca = V c − V a I c = I ca − Ibc VA VA 1.Tres impedancias de valor 4+3j se conectan en estrella y se les aplica un sistema trifásico equilibrado de tensiones con una tensión de línea en secuencia directa de 380V. Halla las intensidades de línea y las tensiones entre los extremos de cada impedancia. Dibuja el diagrama vectorial. 2.Tres reactancias inductivas de valor 2, 3, y 4 ohmios se conectan en estrella trifásica con 380V de tensión de línea con hilo neutro. Halla las intensidades de línea y la del neutro. Dibuja el diagrama vectorial. 3.Tres impedancias compuestas cada una por una resistencia de 100 ohmios y un condensador de 200 microfaradios se conectan en triángulo. Si la tensión de línea trifásica es de 220V y la frecuencia de 50 Hz halla las intensidades de fase y de línea y dibuja el diagrama vectorial. 4.Tres impedancias, Zab=3+4j, Zbc=6-8j, Zca=9+12j se disponen en triángulo y conectadas a una tensión de línea trifásica de 220V y 50 Hz. Halla las intensidades de línea, de fase y dibuja el diagrama vectorial. 5.Un sistema trifásico está compuesto por tres impedancias que constan de una resistencia de 5 ohmios en serie con una bobina de 20 mH. Las tres impedancias se colocan en triángulo y se les somete a un sistema trifásico con tensión de línea de 380V y 50 Hz. Halla la potencia activa, y la reactiva absorbidas por el sistema. Hállalo también si se colocasen en estrella con la misma tensión de línea. 6.La potencia activa consumida por una carga conectada a una línea de 220V es de 2000W y su ángulo de desfase 53º inductivos. Halla las potencias reactiva y aparente así como la intensidad de línea dibujando el triángulo de potencias. 7. A una red de 380 V de tensión de línea se le conectan en paralelo dos cargas equilibradas cuyas potencias activas son de 3000 W y 4000W cuyos ángulos de desfase respectivos son de 45º y 60º. Dibuja el triángulo de potencias total, halla la intensidad de línea y el desfase de la carga equivalente. 8.A una línea trifásica de tensión de línea 400V y f=50Hz, se conecta un receptor en estrella formado cada rama por una resistencia y una bobina en serie. La potencia en cada una de las tres ramas es de 10kW (activa) y 8kVAr (reactiva). Calcular: a) Factor de potencia de la carga. b) Intensidades de línea, indicando módulo y argumento. c) Valor de R y XL. 9.A una línea trifásica de tensión de línea 400V y f=50 Hz, se conectan tres receptores: el primero consume 10KW con cosϕ=1 , el segundo consume 12KW con cosϕ =0,9 inductivo, y el tercero consume 5 KW con cosϕ =0,85 capacitivo. Calcular : a) Triángulo de potencias. b) Capacidad de cada condensador de la batería de condensadores a conectar en triángulo para mejorar el factor de potencia a 1. 10.A una línea trifásica de tensión de línea 400V y f=50Hz, se conecta un receptor en estrella formado cada rama por una resistencia y una bobina en serie. La potencia en cada una de las tres ramas es de 5kW (activa) y 4kVAr (reactiva). Calcular: a) Intensidades de línea e intensidades de fase, indicando módulo y argumento. b) Valor de R y XL. 11.A una línea trifásica de tensión de línea 400V y f=50 Hz, se conecta un receptor que consume una potencia de 25KW con un cosϕ =0,75 inductivo, calcular : a) Triángulo de potencias. b) Capacidad de cada condensador de la batería de condensadores, a conectar en triángulo, necesaria para elevar el cosϕ a 0,9. 12.A una línea trifásica de tensión de línea 400V y f=50 Hz, se conecta un receptor que consume una potencia de 3,6KW con un cosϕ 0,75 inductivo. a) Realizar el esquema y calcular el triángulo de potencias. b) Capacidad de cada condensador de la batería de condensadores, a conectar en triángulo, necesaria para elevar el cosϕ a 0,9. 13.A una línea trifásica de tensión de línea 380V y f=50Hz, se conecta en estrella un receptor trifásico formado en cada rama por una resistencia y una bobina en serie (iguales las tres ramas). La potencia consumida por el conjunto de las tres ramas es de 1150W (activa) y 1150VAr (reactiva). Calcular : a) El valor de R y L. b) Intensidad de línea. c) Factor de potencia de la carga. 14.A una línea trifásica de tensión de línea 380V y f=50 Hz, se conecta un receptor que consume una potencia de 5 KW con un cosϕ =0,83 inductivo : a) Realizar el esquema y calcular el triángulo de potencias. b) Capacidad de cada condensador de la batería de condensadores, a conectar en triángulo, necesaria para elevar el cosϕ a 0,98. 15.A una línea trifásica de tensión de línea 400V y f=50 Hz, se conectan tres receptores: el primero consume 8KW con cosϕ =1 , el segundo consume 10KW con cosϕ =0,85 inductivo, y el tercero consume 6 KW con cosϕ =0,8 capacitivo. Calcular : a) Triángulo de potencias. b) Capacidad de cada condensador de la batería de condensadores a conectar en triángulo para mejorar el factor de potencia a 1. 16.A una línea trifásica de tensión de línea 400V y f=50 Hz, se conecta un receptor que consume una potencia de 10KW con un cosϕ =0,8 inductivo, calcular : a) Triángulo de potencias. b) Capacidad de cada condensador de la batería de condensadores, a conectar en triángulo, necesaria para elevar el cosϕ a 0,9. 17.A una línea trifásica de tensión de línea 400V y f=50 Hz, se conectan tres receptores: el primero consume 10KW con cosϕ =1 , el segundo consume 15KW con cosϕ =0,8 inductivo, y el tercero consume 4 KW con cosϕ =0,9 capacitivo. Calcular: a) Triángulo de potencias. b) Capacidad de cada condensador de la batería de condensadores a conectar en triángulo para mejorar el factor de potencia a 1. 18.A una línea trifásica 230/400V y f=50 Hz, están conectados tres receptores iguales de resistencia 3Ω e inductancia 4Ω, con un desfase inductivo. Conectados los tres receptores en estrella, calcular: a) Corrientes de línea y de fase, tensión de fase y de línea y potencia total activa. b) Realizar los mismos cálculos en el caso de que conectemos los tres receptores en triángulo. 19.A una línea trifásica de tensión de línea 400V y f=50Hz, se conecta un receptor en estrella formado cada rama por una resistencia y una bobina en serie. La potencia en cada una de las tres ramas es de 2kW (activa) y 1,5kVAr (reactiva). Calcular : a) El valor de R y XL. b) Intensidad de línea. c) Factor de potencia de la carga. 20.A una línea trifásica de tensión de línea 400V y f=50Hz, se conecta un receptor en estrella formado cada rama por una resistencia y una bobina en serie. La potencia en cada una de las tres ramas es de 4kW (activa) y 3kVAr (reactiva). Calcular: a) Intensidades de línea e intensidades de fase, indicando módulo y argumento. b) Valor de R y XL. 21.A una línea trifásica de tensión de línea 400V y f=50Hz, se conecta un receptor en estrella formado cada rama por una resistencia y una bobina en serie. La potencia en cada una de las tres ramas es de 8kW (activa) y 5kVAr (reactiva). Calcular: a) Factor de potencia de la carga. b) Intensidades de línea, indicando módulo y argumento. c) Valor de R y XL.