Cálculos computacionales en Ingeniería Química. Tema 6

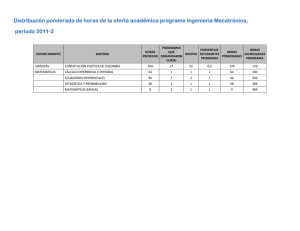
Cálculos computacionales en
Ingeniería Química.
Tema 6
L. Méndez
Departamento de Quı́mica, Universidad Autónoma de Madrid
CCIQ, 2005-06, T4 – p. 1/2
Ecuaciones diferenciales
Definiciones.
Métodos de Euler y Heun.
Método de la serie de Taylor.
Métodos de Runge - Kutta.
Métodos predictor-corrector.
Sistemas de ecuaciones diferenciales.
Problemas de contorno. El método de disparo.
Método de diferencias finitas.
CCIQ, 2005-06, T4 – p. 2/2
Ecuaciones diferenciales ordinarias.
Primer orden: y ′ = f (x, y)
Segundo orden: y ′′ = f (x, y, y ′ )
Sistemas de ecuaciones diferenciales:
y1′ = f1 (x, y1 , y2 )
y2′ = f2 (x, y1 , y2 )
* Condiciones iniciales; por ejemplo: y ′′ = f (x, y, y ′ ) con
y(x0 ) = y0 ; y ′ (x0 ) = y0′
* Condiciones de contorno; por ejemplo: y ′′ = f (x, y, y ′ )
con y(x0 ) = y0 ; y(x1 ) = y1
CCIQ, 2005-06, T4 – p. 3/2
Método de Euler
Consideramos la ecuación y ′ = f (x, y) con la condición inicial y(x0 ) = y0
dy
∆y
En el método de Euler tomamos dx
≈ ∆x
. Paso fijo h:
y1
=
y0 + hf (x0 , y0 )
y2
=
y1 + hf (x1 , y1 )
y3
=
y2 + hf (x2 , y2 ) ...
Comparando con la serie de Taylor:
2
2
h d y dy y(x1 ) = y0 + h
+
+···
dx x=x0
2 dx2 x=x0
obtenemos:
y(x1 ) = y1Euler + O(h2 )
Error local de orden h2
Error global tras N pasos, N =
x−x0
,
h
error de orden N h2 ∼ h
CCIQ, 2005-06, T4 – p. 4/2
Método de Euler.y(x)
y(x)
Error in first step
Exact solution at end of
one step
h f (x0, y0)
y1
Solution given by Eq. (9.24)
at end of one step
y0
Slope
x0
x1
x
h
Figure 9.4
Geometric interpretation of Euler’s method.
© 2002 Prentice Hall, Inc.
Singiresu S. Rao
Applied Numerical Methods for Engineers and Scientists, 1E.
CCIQ, 2005-06, T4 – p. 5/2
y(x)
Método de
Heun.
Exact y(x)
Slope of y at xi
(0)
f (xi 1, yi 1)
Average slope
1
Slope of y at xi
f(xi, yi)
yi
1
(0)
yi 1
xi
xi
x
1
h
Figure 9.8
Graphical interpretation of Heun’s method
© 2002 Prentice Hall, Inc.
Singiresu S. Rao
Applied Numerical Methods for Engineers and Scientists, 1E.
CCIQ, 2005-06, T4 – p. 6/2
El método de Heun
Emplea una pendiente promediada:
h ′
y1 = y0 + [y (x0 ) + y ′ (x1 )]
2
Como no conocemos y ′ (x1 ), la aproximamos empleando el método de Euler. Se trata de un
método predictor-corrector:
Predicción:
y1p = y0 + hf (x0 , y0 )
Corrección:
y1c = y0 + h2 [f (x0 , y0 ) + f (x1 , y1p )]
Puede hacerse una segunda corrección:
c)
y1cc = y0 + h
f
(x
,
y
)
+
f
(x
,
y
0
0
1
1
2
CCIQ, 2005-06, T4 – p. 7/2
Método de la serie de Taylor
Disminuimos el error local del método de Euler añadiendo
términos siguientes:
h2 ′′
y1 = y0 + hf (x0 , y0 ) + y (x0 ) + · · ·
2
Evaluamos las derivadas de orden superior:
df (x, y) ∂f (x, y)
dy ′
y =
=
6=
dx
dx
∂x
df (x, y)
∂f (x, y)
∂f (x, y) dy
=
+
dx
∂x
∂y
dx
′′
Método lento.
Es preciso decidir a priori el número N de términos.
Cálculo complejo de derivadas de orden superior.
CCIQ, 2005-06, T4 – p. 8/2
Métodos de Runge-Kutta.
Partimos de una forma generalizada del método de Euler:
yi+1 = yi + h Φ(xi , yi , h)
donde
Φ = w1 k1 + w1 k2 + · · · + wN kN ,
Los kj se obtienen evaluando f (x, y) en puntos del intervalo [xi , xi+1 ].
El más popular es el método de Runge-Kutta de cuarto orden (N = 4):
yi+1
=
k1
=
k2
=
k3
=
k4
=
h
(k1 + 2k2 + 2k3 + k4 )
6
f (xi , yi )
1
1
f (xi + h, yi + k1 h)
2
2
1
1
f (xi + h, yi + k2 h)
2
2
f (xi + h, yi + k3 h)
yi +
Se obtiene comparando con la serie de Taylor de orden 4 e imponiendo que la diferencia
sea O(h5 )
CCIQ, 2005-06, T4 – p. 9/2
Método de Runge-Kutta-Fehlberg.
Es un método de paso variable. El paso se va adaptando
durante la integración. Para determinar el paso óptimo, se
calcula mediante RK con N = 4 y N = 5, que toman la forma:
4
yi+1
= yi + (a1 k1 + a3 k3 + a4 k4 + a5 k5 )
5
yi+1
= yi + (b1 k1 + b3 k3 + b4 k4 + b5 k5 + b6 k6 )
A continuación el paso h se convierte en sh, donde s se
4
5
− yi+1
| con una tolerancia prefijada
obtiene comparando |yi+1
τ.
CCIQ, 2005-06, T4 – p. 10/2
Métodos predictor-corrector
Son métodos multipaso
Euler, Runge-Kutta son métodos de paso simple: para
obtener yi+1 sólo necesitamos yi
Los métodos predictor-corrector (Milne,
Adams-Moulton..) son métodos de paso múltiple o
multipaso: para obtener yi+1 empleamos la información
en varios puntos anteriores xi , xi−1 , xi−2 , · · ·
En general los métodos predictor-corrector son más rápidos y
exactos que los Runge-Kutta, pero pueden ser inestables:
Los errores aumentan y van cambiando de signo al avanzar
el proceso de integración.
CCIQ, 2005-06, T4 – p. 11/2
Método de Milne.
4
4
3.5
xi+1
3.5
3
3
Construcción corrector Milne
2.5
2.5
f(x,y)
f(x,y)
Construcción predictor Milne
2
1.5
2
1.5
xi
i−3
xi−2
1
i
x
xi−1
i−2
0.5
0
x
xi−3
x
1
xi−1
0.5
0
1
2
3
4
0
0
1
x/h
Predicción:
y4p
2
3
4
x/h
= y0 +
R x4
x0
P123 (x)dx
Fórmula de integración abierta (Newton-Cotes de 3 puntos)
R x4
c
Corrección: y4 = y2 + x2 P234 (x)dx
Fórmula de integración cerrada (Simpson 1/3)
CCIQ, 2005-06, T4 – p. 12/2
3
3
2.5
2.5
2
2
Predictor ABM
f(x,y)
f(x,y)
Método de Adams-Bashforth-Moulton.
1.5
xi+1
Corrector ABM
1.5
x
i−3
xi−3
1
1
x
i−2
i−2
1
x
0.5
i−1
0
i
x
x
0.5
0
x
i
x
2
3
4
0
i−1
0
1
x/h
Predicción:
2
3
4
x/h
y4p
= y3 +
R x4
x3
P0123 (x)dx
= y3 +
R x4
P1234 (x)dx
Integración abierta
Corrección:
y4c
x3
Integración cerrada
CCIQ, 2005-06, T4 – p. 13/2
Método de Adams-Bashforth-Moulton.
Predictor:
y4p
h
= y3 + (55f3 − 59f2 + 37f1 − 9f0 )
24
Corrector
y4c
h
= y3 + (9f4 + 19f3 − 5f2 + f1 )
24
Para aplicar el método es necesario utilizar otro método de
arranque (por ejemplo Runge-Kutta) que proporcione
y1 , y2 , y3
CCIQ, 2005-06, T4 – p. 14/2
Sistemas de ecuaciones diferenciales de primer orden.
Consideramos sistemas de la forma:
dx
= f1 (t, x, y)
dt
dy
= f2 (t, x, y)
dt
con la condición inicial x(t0 ) = x0 ; y(t0 ) = y0 .
En notación matricial:
y ′ = f (t; y);
y(t0 ) = y0
CCIQ, 2005-06, T4 – p. 15/2
Sistemas de ecuaciones diferenciales de primer orden.
En general se aplican los mismos métodos numéricos que
para ecuaciones; por ejemplo:
Euler:
y1 = y0 + hf (t, y0 )
Taylor:
2
h df y1 = y0 + hf (t, y0 ) +
+···
2 dt x0
CCIQ, 2005-06, T4 – p. 16/2
Sistemas de ecuaciones diferenciales de primer orden.
Runge-Kutta (N=4)
yi+1
=
k1
=
h
(k + 2k2 + 2k3 + k4 )
6 1
f(ti , yi )
k2
=
f(ti +
k3
=
k4
=
yi +
1
1
h, yi + k1 h)
2
2
1
1
f(ti + h, yi + k2 h)
2
2
f(ti + h, yi + k3 h)
CCIQ, 2005-06, T4 – p. 17/2
Sistemas de ecuaciones diferenciales de primer orden.
ABM (lo escribo explícitamente para un sistema de 2 ecuaciones diferenciales):
Predictor:
h
[55f1 (ti , xi , yi ) − 59f1 (ti−1 , xi−1 , yi−1 ) +
24
+37f1 (ti−2 , xi−2 , yi−2 ) − 9f1 (ti−3 , xi−3 , yi−3 )]
h
= yi +
[55f2 (ti , xi , yi ) − 59f2 (ti−1 , xi−1 , yi−1 ) +
24
+37f2 (ti−2 , xi−2 , yi−2 ) − 9f2 (ti−3 , xi−3 , yi−3 )]
xpi+1 = xi +
p
yi+1
Corrector
h
p
[9f1 (ti+1 , xpi+1 , yi+1
) + 19f1 (ti , xi , yi ) −
24
−5f1 (ti−1 , xi−1 , yi−1 ) + f1 (ti−1 , xi−1 , yi−1 )]
h
p
= yi +
) + 19f2 (ti , xi , yi ) −
[9f2 (ti+1 , xpi+1 , yi+1
24
−5f2 (ti−1 , xi−1 , yi−1 ) + f2 (ti−1 , xi−1 , yi−1 )]
xci+1 = xi +
c
yi+1
CCIQ, 2005-06, T4 – p. 18/2
Problemas de contorno. Método de disparo.
Comenzamos por un ejemplo sencillo: Una barra metálica a temperatura T , superior a la del
entorno Ta . El enfriamiento de esta barra viene descrito por la ecuación:
d2 T
= k(T − Ta )
dx2
donde x es la distancia.
Condición de contorno: T (x = 0) = T0 ; T (x = l) = Tl .
Método de disparo:
Se convierte la ecuación en un sistema de ecuaciones diferenciales de primer orden:
dT
dx
dz
dx
Condición inicial:
=
z
=
k(T − Ta )
T (x = 0) = T0 . No conocemos z(x = 0).
CCIQ, 2005-06, T4 – p. 19/2
Método de disparo.
En el método de disparo se resuelve el sistema con distintos valores z(x = 0) = α y se
busca α para que T (x) cumpla la otra condición de contorno (T (α, x = l) = Tl ); es decir, α
es solución de la ecuación:
T (α, x = l) = Tl
donde T (α, x) es solución del sistema con condición inicial z(x = 0) = α.
Puede generalizarse a ecuaciones de mayor orden.
En general requiere un proceso iterativo para encontrar la condición inicial apropiada
del sistema de ecuaciones diferenciales (en nuestro el valor de α).
En general es un método lento,
CCIQ, 2005-06, T4 – p. 20/2
Método de diferencias finitas.
Consideramos el problema de contorno del ejemplo anterior:
d2 T
= k(T − Ta ) con :T (x = 0) = T0 ; T (x = l) = Tl
dx2
En este método se sustituyen las derivadas por diferencias divididas (ver tema 5, diferencias
centrales):
d2 T
dx2
≈
Ti+1 − 2Ti + Ti−1
h2
donde Tk = T (xk ) = T (kh). Obtenemos:
Ti+1 − 2Ti + Ti−1
2
2
−
k(T
−
T
)
=
0
⇒
−
T
+
T
(2
+
kh
)
−
T
=
kT
h
a
a
i
i+1
i
i−1
h2
Estas ecuaciones (para los nodos interiores), junto con las condiciones de contorno
constituyen un sistema de ecuaciones lineales, tridiagonal cuya solución es la temperatura
en los puntos xi
CCIQ, 2005-06, T4 – p. 21/2
Método de diferencias finitas.
Más en general, dado un problema de contorno:
y ′′ = p(x)y ′ (x) + q(x)y(x) + r(t); y(a) = α, y(b) = β
Se emplea el siguiente esquema:
1. Se aproxima:
y′
≈
y ′′
≈
yi+1 − yi−1
+ O(h2 )
2h
yi+1 − 2yi + yi−1
2
+
O(h
)
h2
2. Se sustituyen estas aproximaciones en la ecuación diferencial y se eliminan términos
de orden O(h2 )
3. Se resuelve el sistema de ecuaciones lineales tridiagonal con incógnitas {yk }
CCIQ, 2005-06, T4 – p. 22/2