fase final (12-v-2012)
Anuncio

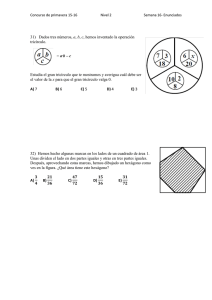
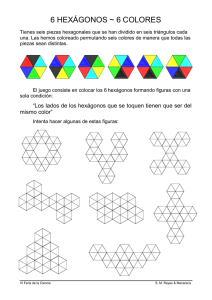
10ª OLIMPIADA MATEMÁTICA DE EUSKADI 2011-12 OLIMPIADA EDUARDO CHILLIDA 2º curso E.S.O. FASE FINAL (12-V-2012) 1.- ¿CUÁNTOS SIETES? ¿Qué proporción de números de tres cifras contienen al menos una vez el dígito 7? SOLUCIÓN: En total hay 900 números de tres cifras. Los números que tiene algún 7 se pueden contar separándolos en tres grupos, como se ve en la tabla adjunta: a) Empiezan por 7 b)Tienen el 7 en las decenas y no están en a) c) Tienen el 7 en las unidades y no están ni en a) ni en b) TOTAL DE NÚMEROS CENTENAS (Nº de dígitos) 1 DECENAS (Nº de dígitos) 10 UNIDADES (Nº de dígitos) 10 TOTAL (números) 100 8 1 10 80 8 9 1 72 252 Proporción 252/900 = 7/25 O bien de los 900 números de tres cifras bastaría quitar los que no tienen ningún 7. Estos son: En las centenas hay 8 posibilidades diferentes, en las decenas 9 y en las unidades 9. Luego, en total: 8 x 9 x 9 = 648 900 – 648 = 252 2.- CONSTRUYENDO HEXÁGONOS Siguiendo el patrón de las tres primeras figuras, a) ¿Cuántos triángulos pequeños aparecerán en la cuarta figura? ¿Y en la novena? Explica el método que utilizas para contar b) ¿Puedes generalizar y decir cuántos triángulos pequeños habrá en la figura que ocupe el lugar n? Justifícalo SOLUCIÓN: a) Lado del 1 hexágono Nº de 6 triángulos 2 3 4 5 6 24 54 96 150 216 b) 6 n2 . Observa que una forma de contar puede ser: N=2 n= 3 3.- EL TERRENO Los terrenos de dos agricultores están limitados por la línea ABCD, según la figura adjunta. (AB=30m., BC=24m. y CD=10m.) Acuerdan diseñar un nuevo límite según un segmento AE, con la condición de que se conserven las áreas iniciales. ¿A qué distancia del punto D deberá colocarse el punto E? 7 8 9 486 SOLUCIÓN: El área del triángulo AFE debe ser igual a la del rectángulo BCDF: Area BCDF = 240 Area AFE: 40 x FE /2 = 240 FE = 12 Luego DE = 12m. F E D 10 B C A 4.- LA DIANA Una cuadrilla de 10 amigos lanzan, al azar, 24 dardos cada uno sobre una diana de tipo hexagonal regular que tiene 40 centímetros de lado. Si ningún dardo se ha clavado fuera de la diana hexagonal grande ¿cuántos dardos crees tú que caerán dentro de la zona interior, correspondiente al pequeño hexágono regular? Nota: Se sabe que el segmento AB es igual a 20 centímetros. SOLUCIÓN: Como AB = 20 el lado del hexágono interior también será 20. Los hexágonos son semejantes con razón de semejanza ½, por tanto la razón de las áreas será 1/4 La probabilidad de que un dardo caiga en la zona interior es ¼. Como se lanzaron 240 dados, el resultado más probable sería 60.




![1) [Relación entre grados Celsius (ºC) y grados Farenheit (ºF)]. Se](http://s2.studylib.es/store/data/007299333_1-d4927f65d9dda7e418a5fbfec3abd807-300x300.png)



