Grafos

Capítulo 1
Grafos
1.1. Conjuntos y relaciones
Consideraremos un conjunto como una colección cualquiera de objetos. Un conjunto queda definido por los objetos que a él pertenecen; dichos objetos son los elementos o miembros del mismo. Si x es un miembro del conjunto A, escribimos x ∈ A
y decimos que x pertenece a A; en caso contrario, escribimos x 6∈ A y decimos, análogamente, que x no pertenece a A.
Si cada elemento x de un conjunto A es también miembro de otro conjunto B,
decimos que A es un subconjunto de B, o que A está incluído en B, y escribimos
A ⊂ B. Dos conjuntos A y B son iguales si y solamente si A ⊂ B y B ⊂ A; es decir,
si constan exactamente de los mismos elementos. En ese caso, escribimos A = B.
A veces se emplea también la notación A ⊆ B para la relación de inclusión, y el
símbolo ⊂ se reserva para la inclusión propia, que ocurre cuando A ⊆ B pero A 6= B.
En general, la relación de inclusión propia aparece con menos frecuencia, y usaremos
el símbolo más sencillo para la relación más frecuente, de modo que “⊂” significará
siempre para nosotros “está incluido en o es igual a”.
En lo sucesivo nos ocuparemos predominantemente de conjuntos finitos, que pueden denotarse convenientemente enumerando todos sus elementos. El número de elementos de un conjunto finito A se denomina también a veces su cardinal, y se escribe |A|.
1.1.1. Producto cartesiano
El producto cartesiano de dos conjuntos A y B se define como el conjunto formado
por todos los pares ordenados posibles cuyo primer elemento es un miembro de A y
cuyo segundo elemento es un miembro de B. En notación conjuntista
A × B = {(a, b) | a ∈ A, b ∈ B}
Si los conjuntos involucrados son finitos, es evidente que |A × B| = |A| · |B|.
Por ejemplo, si A es el conjunto de todos los hombres y B el de todas las mujeres,
A× B es el conjunto de todas las parejas (heterosexuales) posibles que pueden formarse
entre ellos. En particular, si no existiesen hombres, A × B sería vacío, y todo bastante
aburrido.
1
Siguiendo con el ejemplo, el producto cartesiano A × B contiene todas las parejas
concebibles, no necesariamente las que existen en la realidad. Consideremos solamente
aquellas parejas hombre-mujer que constituyan un matrimonio. El conjunto R de pares
hombre-mujer (h, m) donde h es un hombre, m es una mujer y h está casado con m
es un subconjunto de A × B. Además, la inclusión R ⊂ A × B es casi seguramente
propia, excepto en una sociedad polígama y extremadamente promiscua. En cualquier
caso, R contiene toda la información que necesitamos sobre el matrimonio en general:
nos dice exactamente quién está casado con quién.
1.1.2. Relaciones
Definimos una relación entre dos conjuntos A y B como un subconjunto R del
producto cartesiano A × B; en símbolos, R ⊂ A × B. El hecho de que (a, b) ∈ R se
suele expresar diciendo que a está relacionado con b, y, de forma abreviada, se suele
escribir como a R b. La negación de a R b se escribe a 6 R b
Una relación binaria en un conjunto A se define como un subconjunto R del producto A × A. El conjunto en el que se establece R suele denominarse dominio de la
relación.
Algunos ejemplos de relaciones binarias son los siguientes:
La relación de igualdad = entre números reales.
La relación “ser hermano de” en el conjunto de los seres humanos.
La relación de orden ≤ entre números reales.
La relación “ser progenitor de” en el conjunto de los seres humanos. Esta relación
contendría todas las parejas ( p, h) de personas cuyo segundo elemento fuese hijo
del primero.
La relación “ser hijo de” en el conjunto de los seres humanos. Esta relación contendría todas las parejas (h, p) de personas cuyo segundo elemento fuese padre
del primero. Es evidente que esta relación se obtiene de la anterior invirtiendo el
orden de todos los pares: se dice que son inversas.
La relación “ser divisor de” entre números naturales, que suele denotarse por el
símbolo |. Por ejemplo, 6 | 24, pero 6 6 | 31. La relación inversa de ésta también
tiene un nombre común: “ser múltiplo de”.
1.1.3. Propiedades de las relaciones
Hay cuatro propiedades de una relación que nos van a interesar especialmente: que
sea reflexiva, simétrica, transitiva o antisimétrica. Discutiremos primero el significado
de las definiciones y daremos al final un resumen formal de las mismas.
Decimos que una relación R es reflexiva si a R a para todo miembro a del dominio
de R. Por ejemplo, la igualdad = y el orden ≤ son relaciones reflexivas. También lo es
la relación “vivir en el mismo domicilio”.
Una relación R es simétrica si para todo par de elementos a, b del dominio de R
se verifica que, si a R b, entonces b R a. Por ejemplo, “ser hermano de” es una
relación simétrica (es muy difícil ser hermano de alguien sin que éste sea hermano de
uno), lo mismo que “estar casado con”. También la igualdad = entre números reales
es una relación simétrica; sin embargo, el orden ≤ no lo es. De modo más interesante,
2
“x ama a y” (comoquiera que se defina) no es una relación simétrica: un amor no tiene
por qué ser correspondido (aunque puede serlo). Basta con que haya un solo amor no
correspondido para que esta relación deje de ser simétrica.
Tampoco es simétrica la paternidad entre seres humanos: x es padre de y no implica
que y sea padre de x (de hecho, en general, lo impide). Notemos la diferencia entre la
paternidad y el amor: mientras que “x ama a y” no implica el recíproco, no lo impide (y
puede amar a x). En cambio, la paternidad difícilmente puede ser recíproca en ningún
caso: si x es padre de y, no es posible que y sea padre de x. Decimos que una relación R
es antisimétrica si, para cualquier par de miembros a, b del dominio, a R b y b R a se
dan simultáneamente sólo cuando a = b.
Por último, otra propiedad muy importante es la transitividad. Decimos que R
es transitiva si para cualquier terna a, b, c de miembros del dominio, las relaciones
a R b y b R c obligan necesariamente a que a R c. Por ejemplo, si R es la relación
de amistad entre seres humanos, es bastante evidente que no es transitiva: a puede ser
amigo de b y b puede serlo de c, mientras que a puede considerar a c muy poco recomendable. Si R fuese transitiva, sería cierto el refrán “los amigos de mis amigos son
mis amigos”.
Sí es transitiva, en cambio, la relación “ser antepasado de”: los antepasados de mis
antepasados son mis antepasados. En cambio, la paternidad no lo es: si x es el padre de
y e y es el padre de z, esto no obliga en absoluto a que x sea el padre de z.
Resumiendo, si R es una relación binaria en el conjunto A, decimos que R es
reflexiva si a R a, para todo a ∈ A
simétrica si a R b → b R a, para todos a, b ∈ A
transitiva si a R b y b R c → a R c, para todos a, b, c ∈ A
antisimétrica si a R b y b R a → a = b, para todos a, b ∈ A
Una relación R se dice que es una relación de equivalencia si es reflexiva, simétrica
y transitiva. El ejemplo por excelencia es la igualdad, pero existen otros ejemplos significativos. Por ejemplo, la relación “ser hermano de” es una relación de equivalencia,
si admitimos el hecho de que uno es hermano de sí mismo.
Dado un elemento a ∈ A del dominio de una relación de equivalencia R, se define
su clase de equivalencia como el conjunto [a] = {x ∈ A | a R x}, es decir, el
conjunto de los elementos relacionados con a en virtud de R. En el ejemplo anterior,
R = “ser hermano de”, la clase de equivalencia de un individuo es el conjunto de todos
sus hermanos (incluyéndolo a él mismo). Obsérvese que las clases de equivalencia de
esta relación son las progenies de cada familia, y toda la humanidad está dividida en
clases disjuntas de hermanos. Este hecho no es casual.
La propiedad más importante de las relaciones de equivalencia la proporciona el
siguiente
Teorema 1 Sea R una relación de equivalencia en un conjunto A. Las clases de equivalencia de R forman una partición de A, es decir, A es la unión de dichas clases de
equivalencia, y dos clases de equivalencia son o iguales o disjuntas.
D EMOSTRACIÓN Obviamente, cada elemento a ∈ A es miembro de una clase de equivalencia: la suya propia. Ello es así porque la relación es reflexiva, de modo que a R a
y, por tanto, a ∈ [a]. Se deduce que A ⊂ ∪a∈A [a], es decir, A es unión de clases de
equivalencia.
3
Por otro lado, sean [x] e [y] dos clases de equivalencia. Si no son disjuntas, existe
un elemento común a ∈ [x] ∩ [y]. Se deduce que
a R x y que a R y
x R aya R y
(pertenencia a [x] e [y])
(simetría)
x Ry
(transitividad)
Por tanto, si z ∈ [x]
x Rzyx R y
(definición de [x])
z Rxyx R y
z R y, o sea, y R z
(simetría)
(transitividad y simetría)
z ∈ [y]
(definición de [y])
y se concluye que [x] ⊂ [y]. Se prueba del mismo modo que [y] ⊂ [x], y por tanto,
que [x] = [y].
Otro tipo de relación de especial interés es la relación de orden (parcial). Se llama
así a una relación que es reflexiva, antisimétrica y transitiva. Como ejemplos típicos
de relaciones de orden tenemos la relación ≤ entre números reales, o la relación de
divisibilidad entre números naturales (“ser divisor de”, denotada por |). Esta última es
relación de orden, puesto que
para todo entero a, se verifica que a|a (reflexividad)
para todo par de enteros a, b, se verifica que si a|b y b|a, entonces existen números k y l con a = kb = kla y kl = 1, de forma que a = b (antisimetría)
para todo trío de enteros a, b, c, si se dan las relaciones a|b y b|c, existen ciertos
naturales k y l que cumplen c = kb = kla, de modo que a|c (transitividad)
La divisibilidad es un buen ejemplo de una relación de orden parcial. En un orden
parcial R no es preciso que una de las dos relaciones a R b o bien b R a se dé. Por
ejemplo, ni 7|69 ni 69|7. Se dice que los elementos en cuestión no son comparables.
Una relación de orden en la que para todo par de elementos a, b del dominio se verifica
que a R b o bien b R a (o ambas) se dice que es de orden total. La relación de orden
habitual entre números, ≤, es un ejemplo de orden total.
Una representación muy conveniente de las relaciones de orden en conjuntos finitos
es su diagrama de Hasse, que definiremos en la sección 1.4.
1.1.4. Clausura transitiva
Vimos en la sección 1.1.3 que la relación “ser ancestro de” es transitiva, pero la paternidad no lo es: el padre de mi padre no es mi padre (suele denominarse abuelo mío).
Sin embargo, existe una vinculación interesante entre la paternidad y la ancestralidad:
los antepasados se obtienen, por lo general, remontándose hacia atrás una o más veces
en la relación de paternidad (un ancestro mío es, o bien mi padre, o bien el padre de mi
padre, o el padre de mi padre de mi padre, etc.)
Del mismo modo, la relación “ser sucesor de” definida sobre el conjunto de los
enteros no es transitiva: 5 es el sucesor de 4, y 6 es el sucesor de 5, pero 6 no es sucesor
de 4. Como mucho, es mayor que cuatro, y esta relación de orden sí que es transitiva.
4
La relación transitiva que se obtiene por repetición a partir de otra aparece con
frencuencia, lo que motiva la siguiente definición.
Sea R una relación en un conjunto A. Definimos la clausura transitiva de R (a
veces denotada por R ∗ ) como la menor relación transitiva que contiene a R. Más explícitamente,
a) R ⊂ R ∗ ⊂ A × A (es decir, R ∗ es una relación binaria en A).
b) R ∗ es transitiva.
c) Si R ⊂ S ⊂ R ∗ ⊂ A × A y además S es transitiva, entonces S = R ∗ .
Esta definición es muy poco intuitiva, y generalmente utilizaremos esta otra: diremos que a R ∗ b si existe una sucesión {ai } de elementos de A que verifica
a R a 1 R a2 R a3 R · · · R a n R b
es decir, si a está relacionado con un elemento, que está relacionado con otro, que. . . y
así sucesivamente hasta llegar a b. Por ejemplo, la clausura transitiva de la relación de
paternidad es “ser antepasado de”.
1.2. Grafos
1.2.1. Grafo dirigido y no dirigido
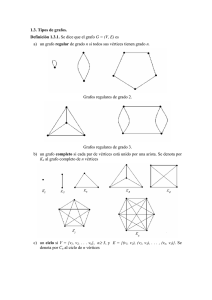
Un grafo (específicamente, grafo simple no dirigido) es un par G = (V, E) =
(V (G), V (E)), donde V es un conjunto finito no vacío de elementos llamados vértices
y E es un conjunto de pares desordenados de elementos distintos de V llamados aristas.
Es decir, una arista e ∈ E tiene la forma {u, v}, donde u, v ∈ V y u 6= v.
La terminología en teoría de grafos varía muchísimo: prácticamente no hay dos
textos que adopten la misma. En paticular, los vértices de un grafo también reciben a
veces el nombre de nodos, y las aristas arcos, ejes o líneas.
Obsérvese que, en un grafo no dirigido conforme con esta definición, los bucles
están excluídos. Por convenio, en grafos no dirigidos designaremos las aristas con la
notación (u, v) que usamos para los pares ordenados de vértices; se sobreentiende que
en las aristas de grafos no dirigidos no importa el orden, es decir, (u, v) = (v, u).
Un grafo se representa por medio de puntos o círculos, que designan los vértices, y
líneas que los unen, que representan las aristas. Por ejemplo, en la figura 1.1(b) tenemos
un ejemplo de grafo no dirigido con conjunto de vértices V = {1, 2, 3, 4, 5, 6} y aristas
E = {(1, 2), (2, 5), (1, 5), (3, 6)}.
Un grafo dirigido o digrafo G es un par (V, E), donde V es un conjunto finito no
vacío y E es una relación binaria en V , es decir, un conjunto de pares ordenados de
elementos de V . Los elementos de V reciben el nombre de vértices. El conjunto E es
el conjunto de aristas de G.
Por ejemplo, en la figura 1.1(a) tenemos un grafo dirigido que, de acuerdo con
la definición, tiene seis vértices (V = {1, 2, 3, 4, 5, 6}) y ocho aristas (E = {(1, 2),
(2, 2), (2, 4), (2, 5), (4, 1), (4, 5), (5, 4), (3, 6)}). Las flechas apuntan del primer elemento de cada par al segundo.
Obsérvese que es posible que una arista puede partir de un vértice y llegar a él de
nuevo. Una arista de esta clase, es decir, de la forma e = (v, v), recibe el nombre de
bucle o lazo.
5
E
F
G
H
I
J
3
+
∗
5
+
6
12 1
χ(K 5 ) = 5
χ(K 3,3 ) = 2
χ(C7 ) = 3
χ(esto) = 4
χ(esto otro) = 4 4
E
F
G
H
I
J
3
+
∗
5
+
6
12
3
1
2
χ(K 5 ) = 5
χ(K 3,3 ) = 2
χ(C7 ) = 3
χ(esto) = 4
5 χ(esto 6otro) = 4 4
(a)
2
3
5
6
(b)
Figura 1.1: Ejemplos de (a) grafo dirigido, y (b) no dirigido
Tipo de grafo
Grafo
Multigrafo
Pseudografo
Grafo dirigido (digrafo)
Multigrafo dirigido
Dirigido
No
No
No
Sí
Sí
Simple
Sí
No
No
Sí
No
Lazos
No
No
Sí
Sí
Sí
Cuadro 1.1: Cadro resumen de los diferentes tipos de grafos
Cuando el sentido de las flechas no nos interesa (o, dicho de forma más técnica, la
relación que el grafo representa es simétrica), es más conveniente el concepto de grafo
no dirigido.
Existen numerosas variantes de las definiciones que acabamos de dar. Por ejemplo, un multigrafo es un grafo no dirigido en el que permitimos la existencia de varias
aristas conectando los mismo vértices y la aparición de bucles. Específicamente, un
multigrafo queda definido por medio de una tríada G = (V, E, f ), donde V y E
son conjuntos y f : E → V × V asigna a cada arista e ∈ E un par desordenado f (e) = {u, v} de vértices diferentes de V (los vértices extremos de la arista e).
Un multigrafo dirigido se define de forma exactamente igual, excepto que el recorrido de f está formado por pares ordenados de vértices. Por último, si permitimos la
existencia de bucles o lazos en un grafo no dirigido, tenemos un pseudografo: se trata
de una terna G = (V, E, f ), donde f : E → V × V asigna a cada arista un par no
ordenado de vértices (posiblemente iguales).
Dado que esta terminología no es estándar, siempre es conveniente en cada caso
especificar claramente si el grafo objeto de nuestra consideración es dirigido o no; si se
admiten múltiples aristas entre un par cualquiera de vértices (es decir, si el grafo es o
no simple); y si se admiten bucles o lazos. En el cuadro resumen 1.1 se esquematizan
los valores de estos parámetros para las definiciones recién dadas.
1.2.2. Incidencia y grado
Si (u, v) es una arista de un grafo dirigido, decimos que incide desde o sale de el
vértice u, que será su vértice inicial, y que incide hacia o entra en el vértice v, que será
su vértice final. Si estamos en un grafo no dirigido, decimos que (u, v) simplemente
incide en los vértices u y v, que serán sus vértices extremos.
Por ejemplo, en la figura 1.1(a), hay tres aristas que salen del vértice 2: son (2, 2),
6
(2, 4) y (2, 5). En el grafo no dirigido de la figura 1.1(b), la arista (3, 6) incide en los
vértices 3 y 6.
Si (u, v) es una arista de un grafo, decimos que el vértice v es adyacente al vértice u. En un grafo no dirigido, la relación de adyacencia es simétrica; no es así necesariamente en un digrafo. Por ejemplo, en la figura 1.1(a), el vértice 5 es adyacente al 2
(pero el 2 no es adyacente al 5). En cambio, en el grafo de la figura 1.1(b), los vértices
1 y 2 son adyacentes entre sí.
El grado de un vértice en un grafo no dirigido es número de aristas incidentes con
él. Por ejemplo, el vértice 5 de la figura 1.1(b) tiene grado 2. En un digrafo, el grado
de salida de un vértice es el número de aristas que salen de él, y el grado de entrada
es el número de aristas que entran en él. El grado es la suma de los grados de salida
y entrada. En el grafo dirigido de la figura 1.1(a), el vértice 2 tiene grado de salida 3,
grado de entrada 2 y grado 5.
1.2.3. Representación como estructuras de datos
Nuestro interés en los grafos radica en su aplicación a la informática, y exige que
podamos representarlos en nuestros programas como estructuras de datos que podamos
manejar, crear, modificar y consultar. Existen tres representaciones usuales de los grafos que permiten su manipulación como objetos en nuestros programas: las representaciones por medio de matrices de adyacencia, de listas de adyacencia y de matrices
de incidencia.
En la representación por matrices de adyacencia, un grafo G = (V, E) cuyo conjunto de vértices sea V = {a1 , a2 , . . . , an } se representa por una matriz booleana M,
cuadrada, de dimensión igual al número de vértices n, y cuyos elementos se definen
por
(
1 si (ai , a j ) es una arista de G
Mi j =
0 en caso contrario
Es decir, la matriz M representa la relación de adyacencia. Habrá un uno en la fila i ,
columna j , si hay una arista que va del vértice ai al vértice a j .
Obsérvese que la matriz no será simétrica, en general, si el grafo es dirigido. En
cambio, la matriz de adyacencia de un grafo no dirigido siempre será simétrica. Las
aristas múltiples no quedan bien representadas en la matriz de adyacencia, pero sí los
bucles o lazos, que provocan la presencia de unos en la diagonal principal.
Para el grafo de la figura 1.1(a), la matriz de adyacencia se representa en la figura 1.2(a).
La representación por matrices de adyacencia tiene un inconveniente serio para
grafos grandes: el tamaño de la matriz es proporcional al cuadrado del número de
vértices. Si el número de aristas |E E| es comparativamente pequeño en relación a |V | 2 ,
se desperdicia una cantidad enorme de espacio. La mayoría de los grafos se encuentra
en este caso: son grafos dispersos, donde |E| |V |2 .
La representación por listas de adyacencia es mucho más conveniente en esta mayoría de casos. Un grafo G = (V, E) se representará por un vector de listas. El vector
tiene |V | posiciones, una por cada vértice; en la posición i -ésima se almacena la lista
de los vértices adyacentes a ai . En la figura 1.2(b) representamos el grafo de la figura 1.1(a) por medio de listas de adyacencia.
Podemos ver que el tamaño de esta representación es proporcional al número |E|
de aristas del grafo. Esto lo hace mucho más conveniente en casi todos los casos. Sola-
7

0
0

0
M =
1

0
0
1
1
0
0
0
0
0
0
0
0
0
1
0
1
0
0
1
0
0
1
0
1
0
0

0
0

0

0

0
0
Vértice
1
2
3
4
5
6
Adj(V )
{2}
{2, 4, 5}
{}
{1, 5}
{4}
{3}
(b)
(a)
Figura 1.2: Representación del grafo de la figura 1.1(a) por medio de a) matriz de
adyacencia b) listas de adyacencia
mente en el caso de grafos densos (en los que |E| y |V |2 son comparables) es razonable
considerar la matriz de adyacencia como representación alternativa.
La matriz de incidencia de un grafo G = (V, E), donde |V | = n y |E| = m se
define como una matriz booleana n × m en la que
(
1 si la arista j incide en el vértice i
(Minc )i j =
0 en caso contrario
Esta representación es solamente válida para grafos no dirigidos, puesto que el sentido de las aristas no puede ser representado de esta forma. Puede resultar útil para
representar multigrafos, pero su interés fundamental es más bien teórico.
1.2.4. Caminos y ciclos
Un camino de longitud k entre el vértice u y el vértice u 0 del grafo G = (V, E) es
una sucesión de aristas {e1 , e2 , . . . , ek } tales que ei = (vi−1 , vi ) para i = 2, 3, . . . , k,
con lo que cada arista tiene por vértice inicial el vértice final de la anterior. Para hacer
explícito este hecho, a veces un camino se denota también con los vértices intercalados: C = {v0 , e1 , v1 , . . . , en , vn }. Si no hay ambigüedad, un camino puede denotarse
exclusivamente por la sucesión de vértices que visita: C = {v0 , v1 , . . . , vk }. Esto puede
hacerse, por ejemplo, cuando los grafos con los que trabajamos son simples.
La longitud del camino, según la definición dada arriba, es el número de aristas que
lo constituyen. El vértice inicial de C = {v0 , e1 , . . . , ek , vk } es v0 , y el vértice final es
vk .
Un camino es simple si todas sus aristas son distintas. En ocasiones se llama simple
a un camino que no visita dos veces el mismo vértice. La segunda definición es más
restrictiva que la primera, puesto que un camino puede pasar dos veces por un mismo
vértice sin visitar ninguna arista más de una vez.
Un camino (v0 , e1 , v1 , . . . , ek , vk ) forma un ciclo si v0 = vk y el camino contiene
al menos una arista. El ciclo es simple si, además, las aristas que lo forman son todas
distintas. Por ejemplo, un lazo es un ciclo de longitud unidad.
8
1.3. Accesibilidad y conexión
Decimos que un vértice u 0 de un grafo es accesible (o alcanzable) desde otro vértice u si existe un camino de u a u 0 .
Es fácil ver que la relación de accesibilidad es transitiva: si w es accesible desde v
y v es accesible desde u, es evidente que w es accesible desde u. Además, todo nodo
es accesible desde sí mismo (por medio de un camino de longitud cero). En un grafo
no dirigido, la relación también es simétrica; en un digrafo ya no tiene por qué ser así
(en la figura 1.1(a), el vértice 3 es accesible desde 6, pero no al contrario).
Un grafo no dirigido es conexo si cada par de vértices está conectado por un camino
(es decir, todos los vértices son mutuamente accesibles). Las componentes conexas de
un grafo son las clases de equivalencia de los vértices bajo la relación de accesibilidad.
El grafo de la figura 1.1(b) no es conexo, ya que, por ejemplo, 6 es inaccesible desde 1.
Hay tres componentes conexas en el grafo: {1, 2, 5}, {3, 6} y {4}.
En una componente conexa, todos los vértices son mutuamente accesibles; es evidente, por tanto, que un grafo es conexo si y solamente si tiene una única componente
conexa. Intuitivamente, las componentes son los diferentes “trozos” conexos en que el
grafo se descompone.
Un grafo dirigido es fuertemente conexo si cualquier vértice es accesible desde
cualquier otro. Las componentes fuertemente conexas de un digrafo son las clases de
equivalencia de los vértices bajo la relación “ser mutuamente accesibles”.
Es algo menos intuitivo visualmente el extraer las componentes fuertemente conexas de un digrafo. Por ejemplo, en el grafo de la figura 1.1(a), tenemos tres componentes: {1, 2, 4, 5}, {3} y {6}. Los cuatro vértices que residen en la primera componente
son mutuamente accesibles entre sí (basta usar el ciclo (1, 2, 5, 4) para desplazarse de
un vértice a otro); pero 3 y 6 no son mutuamente accesibles (solamente 3 es accesible
desde 6, pero no a la inversa), y por consiguiente residen en componentes distintas.
1.4. Relaciones y grafos
Existe una conexión muy íntima entre las relaciones binarias en un conjunto y los
grafos. De hecho, hemos definido un grafo dirigido como una relación, y el uso que
hacemos de los grafos en informática es para representar relaciones.
Sea A un conjunto finito y R una relación binaria de dominio A. Al ser A finito,
podremos enumerar sus elementos:
A = {a1 , a2 , a3 , . . . , an }
Definimos el grafo asociado a R (o grafo que representa R) como un grafo cuyos
vértices son los elementos de A, siendo (ai , a j ) una arista del grafo si y solamente
si ai R a j . De hecho, según la definición de digrafo que dimos en la sección 1.1(b), la
propia relación es un grafo.
Como ejemplo, consideremos la relación binaria R definida entre números enteros
como sigue
a R b si y solamente si b = pa con p primo
y estudiemos su restricción al conjunto A = {1, 2, 3, 4, 6, 9, 12, 18, 36} formado por
los divisores de 36. El grafo asociado a la relación será el que se muestra en la figura 1.3(a). En cambio, el grafo de la relación ≤ entre los números {3, 4, 6, 9} puede
verse en la figura 1.3(b).
9
Zapatero
Zorrilla
A
B
C
D
E
F
G
H
I
J
3
+
∗
5
+
64
12
χ(K 5 ) = 5
χ(K 3,3 ) = 2
χ(C7 ) = 3
χ(esto) = 4
χ(esto otro) = 4
Zapatero
Zorrilla
A
B
C
D
E
F
G
H
I
J
36
3
+
12
18
∗
5
+
6
6
9
12
χ(K 5 ) = 5
χ(K
3 3,3 ) = 2
2
χ(C7 ) = 3
χ(esto) = 4 3
1χ(esto otro) = 4
(a)
6
4
9
(b)
Figura 1.3: (a) Retículo de divisores de 36 y (b) Relación de orden entre 3, 4, 6, 9
Algunas propiedades de estas relaciones son directamente observables a partir del
grafo. Por ejemplo, en ninguna de las figuras encontramos flechas dirigidas en sentidos
contrarios entre ningún par de nodos. Esto se debe a que las relaciones representadas
son antisimétricas. La relación de orden de la figura 1.3(b) es, además, obviamente
reflexiva: la presencia de un bucle o lazo en todos y cada uno de los nodos lo prueba.
Observemos que 2 R 6 y que 6 R 12, pero que, sin embargo, 2 6 R 12. Esto se debe
a que la relación R no es transitiva. En cambio, ≤ sí es una relación transitiva; veremos
enseguida en qué se traduce esto en términos de grafos.
Un ejemplo de grafo que se vincula a una relación de manera algo diferente es
el diagrama de Hasse de una relación de orden. El diagrama de Hasse se obtiene
representando la relación por un grafo, y suprimiendo
todos los lazos
todas las aristas que se puedan deducir por transitividad de otras dos
En la figura 1.3(a) tenemos un ejemplo de un tal diagrama para la relación de divisibilidad en el conjunto de los divisores de 36.
La matriz de adyacencia del grafo asociado a una relación R se denomina simplemente matriz de la relación; es una matriz cuadrada binaria M R , de dimensión igual al
cardinal del dominio de R. El elemento (M R )i j de la matriz vale uno o cero según que
los elementos ai y a j estén relacionados o no. En símbolos,
(
1 si ai R a j
(M R )i j =
0 en caso contrario
Veamos cómo se plasman en términos de grafos y de matrices de relaciones las
cuatro propiedades estudiadas en 1.1.3.
reflexividad R es reflexiva sii a R a para todo a ∈ A. Por lo tanto, si cada vértice del
grafo posee un lazo, R es reflexiva; si algún vértice carece de lazo, la relación no
es reflexiva. En términos de matrices, cada elemento de la diagonal principal
de M R debe ser un uno.
10
D
E
F
G
H
I
J
3
+
∗
5
+
6
12
χ(K 5 ) = 5
χ(K 3,3 ) = 2
χ(C7 ) = 3
χ(esto) = 4
χ(esto otro) = 4
K4
K5
K6
Figura 1.4: Grafos completos de cuatro, cinco y seis vértices
simetría R es simétrica sii a R b ⇒ b R a, para todo par de a, b ∈ A. Por lo tanto,
si hay una flecha de un vértice v a otro w, la flecha contraria también debe estar
presente; y si no la hay en un sentido, la contraria tampoco puede existir. En
términos matriciales, (M R )i j = (M R ) j i para todo par de índices i, j ; o, más
brevemente, M R es simétrica: M Rt = M R
transitividad R es transitiva si y solamente si a R b junto con b R c implica necesariamente que a R c. En términos de grafos, la existencia de una arista entre los
vértices a, b y otra entre b, c implica la existencia de la arista (a, c). El par de
aristas (a, b), (b, c) forma un camino de longitud dos entre los vértices a y c, de
modo que la condición de transitividad puede formularse así: la accesibilidad de
orden dos implica adyacencia. En términos matriciales, (M R )2i j = 1 implicará
siempre que (M R )i j = 1 o, abreviando, M R2 ⊂ M R : elevar al cuadrado la matriz
de la relación no introduce unos que no existieran ya en M R .
1.5. Algunos grafos especiales
1.5.1. Grafos completos
Un grafo completo es un grafo no dirigido en que todos los vértices son adyacentes
entre sí. Para cada número de vértices n, existe esencialmente un solo grafo completo
(todos son isomorfos entre sí), que se designa por K n . Por ejemplo, en la figura 1.4
tenemos algunos grafos completos.
Teorema 2 El grafo completo de n vértices K n tiene n2 = n(n − 1)/2 aristas.
Hay varias formas de demostrar esto:
1. El número de aristas de K n es el número de pares desordenados en un conjunto
de n objetos, es decir, el de combinaciones de n elementos tomados de dos en
dos.
2. Cada vértice del grafo está unido a los n − 1 restantes. Si contamos las aristas
incidentes en cada uno de los n vértices, obtenemos n(n − 1), pero, al obrar
así, estamos contando cada arista dos veces (puesto que tiene dos extremos). Por
tanto, el número total de aristas es exactamente la mitad, n(n − 1)/2.
11
12
Propiedad
Definición
Reflexiva
∀a
a R
Simétrica
Antisimétrica
∀a, b
∀a, b
a R
a R
Transitiva
∀a, b, c a R
P60 Q
Q
2 4
CQ
m1 Q
Q
Q
3
Q
02 5
Q
QAbad
4
Q
Q
Abascal
Q135
Q
Q24
Álvarez
Abad
Q
Q35
Bastardo
Abascal
Q
Cobas
4
Abad
Álvarez
Cazorla
Q5
Abascal
Bastardo
Dehesa
Cobas
Abad
Álvarez
González
Abascal
Cazorla
Bastardo
Guzmán
Dehesa
Cobas
Álvarez
Herrero
González
Cazorla
Bastardo
Lebrel
Guzmán
Dehesa
Cobas
Zapatero
Herrero
González
Cazorla
Zorrilla
Lebrel
Guzmán
Dehesa
Zapatero
Herrero A
González
Lebrel B
Zorrilla
Guzmán
Zapatero
A C
Herrero
B D
Lebrel
Zorrilla
C
Zapatero
A E
F
D
B G
Zorrilla
E H
C
A
F I
D
B
G
E J
C
H
F 3
D
G
EJI +
H
F3 ∗
I 5
G
+
J∗ +
H
3
6
I
+
J∗5 12
+
χ(K 5 )36
5= 5
χ(K 3,312
)+
=2
+
∗
χ(Kχ(C
65= 3Grafo
5) =
7 )5
+2= 4
χ(Kχ(esto)
3,3 ) =12
χ(K
)) =
65
χ(C57otro)
=12
3= 4
χ(esto
a
χ(K
)
=
2
3,3
χ(esto)
=
4
χ(K
)
=
5
57 ) = 3
χ(C
otro)
=
4
b ⇒ bχ(esto
R aχ(K
)
=
2
3,3 = 4
χ(esto)
χ(C
7 ) b=
χ(esto
otro)
= 34
byb R
a⇒
a
=
χ(esto)
=4
b y b χ(esto
R c ⇒ otro)
a R c= 4
Matriz
(M R )ii = 1 ∀i
M Rt = M R
(M R )i j 6= (M R ) j i
M R2
⊂ MR
Cuadro 1.2: Cuadro resumen de las propiedades de las relaciones
∀i 6= j
Zorrilla
A
B
C
D
E
F
G
H
I
J
3
+
∗
5
+
6 3
12
χ(K 5 ) = 5
χ(K 3,3 ) = 2
χ(C7 ) = 3
χ(esto) = 4
χ(esto otro) = 4
2
1
4
6
5
Figura 1.5: Torneo de seis vértices
3. Numeremos los vértices de 1 a n. En el vértice 1 inciden n − 1 aristas:
(1, 2), (1, 3), (1, 4), . . . (1, n)
En el vértice 2 inciden también n − 1 aristas, pero una ya ha sido contada anteriormente, de modo que sólo aparecen aquí n − 2 nuevas:
(2, 3), (2, 4), . . . (2, n)
Si proseguimos así el recuento, llegamos a que el número total de aristas es la
suma de una progresión aritmética:
|E| = (n − 1) + (n − 2) + · · · + 2 + 1 = (n − 1)
(n − 1) + 1
2
De este teorema deducimos que un grafo simple no dirigido de n vértices tendrá, a
lo sumo, n2 aristas.
1.5.2. Torneos
Un torneo (tournament) es un grafo dirigido cuya versión no dirigida es un grafo
completo. Podemos decir que un torneo puede obtenerse a partir de un grafo completo
asignando orientaciones a cada una de las aristas. En la figura 1.5 podemos ver un
ejemplo de torneo con seis vértices.
En el torneo de la figura podemos ver que el camino simple (1, 2, 4, 6, 3, 5) pasa
por todos los vértices. Un camino así se denomina camino hamiltoniano. En el teorema 8 veremos que siempre es posible encontrar uno en cualquier torneo.
1.5.3. Grafos bipartitos
Un grafo bipartito es un grafo no dirigido G = (V, E) cuyo conjunto de vértices
V es unión de dos conjuntos disjuntos V1 y V2 de forma que (u, v) ∈ E implica que,
o bien u ∈ V1 y v ∈ V2 , o bien u ∈ V2 y v ∈ V1 . Es decir, todas las aristas tienen un
extremo en cada uno de los conjuntos V1 y V2 .
Recordemos que V1 y V2 forman una partición de V si son disjuntos y su unión
es V .
13
D
E
F
G
H
I
J
3
+
∗
5
+
6
12
χ(K 5 ) = 5
χ(K 3,3 ) = 2
χ(C7 ) = 3
χ(esto) = 4P6
χ(esto otro) = 4
C5
C7
Figura 1.6: Camino P6 y ciclos C7 y C5
Teorema 3 Un grafo es bipartito si y solamente si carece de ciclos de longitud impar
D EMOSTRACIÓN Sea G bipartito y C = (v0 , v1 , . . . , vn ) un ciclo de G. Como cada
arista (vi−1 , vi ) une un elemento de V1 con uno de V2 , se deduce que vértices consecutivos de C pertenecen a lados distintos de la partición, de forma que los vértices de
subíndice par están todos en un lado y los de subíndice impar en el contrario. Como
v0 = vn , se deduce que n tiene la misma paridad que 0, es decir, es par.
Recíprocamente, supongamos que el grafo G carece de ciclos de longitud impar.
En primer lugar, es obvio que bastará probar que cada componente de G es bipartita,
así que podemos suponer G conexo. Sea v0 ∈ V (G) un vértice cualquiera, y definamos
V1 = {v ∈ V (G) | existe un camino de longitud impar entre v0 y v}, y V2 = V − V1 .
Por definición, los caminos entre v0 y cualquier vértice de V2 serán todos de longitud
par. Además, V1 y V2 forman una partición de V . Ahora, si dos vértices v, w de V1
son adyacentes, los caminos de longitud impar que los unen con v 0 , más las arista
(v, w), constituyen un ciclo impar, contra la hipótesis. Por lo tanto, no hay ningún par
de vértices adyacentes en V1 . Para V2 , el mismo razonamiento es válido, de forma que
cualquier arista une algún vértice de V1 con alguno de V2 .
1.5.4. Caminos y ciclos
El camino de longitud n es el grafo Pn = (V, E), donde V = {v0 , v1 , . . . , vn }
y E = {(v0 , v1 ), (v1 , v2 ), . . . , (vn−1 , vn )}. El ciclo de longitud n es el grafo C n =
(V, E), donde V = {v1 , . . . , vn } y E = {(vn , v1 ), (v1 , v2 ), . . . , (vn−1 , vn )}. En la
figura 1.5.4 podemos ver ejemplos de estos complicadísimos conceptos.
1.5.5. Grafos cúbicos Q n
Los grafos Q n son la representación de la red de vértices y aristas de un cubo ndimensional. El cubo de dimensión cero Q 0 consta, por definición, de un solo vértice.
A partir de ahí, se obtiene Q n uniendo por medio de aristas los vértices correlativos de
dos copias de Q n−1 . En la figura 1.7 podemos ver los primeros grafos cúbicos, hasta el
de dimensión 4.
1.6. Arboles
Un árbol es un grafo no dirigido, conexo y acíclico. Un grafo no dirigido que es
acíclico, pero posiblemente no conexo, se denomina bosque.
14
Abascal
Abascal
9
9A
9
A
A
Álvarez
Álvarez
12
12 B
12
B
B
Bastardo
Bastardo
18
18 C
18
C
C
Cobas
Cobas
36
36
36
D
D
D
Cazorla
Cazorla
C1
C1 E
C1
E
E
Dehesa
Dehesa
C2
C
C2
2F
F
F
González
González
C3
C3 G
C3
G
G
Guzmán
Guzmán
C4
C4 H
C4
H
H
Herrero
Herrero
C5
C5 I
C5
I
I
Lebrel
Lebrel
C7
C
C7
7 J
J
J
Zapatero
Zapatero
P6
P
P6
6 3
3
3
Zorrilla
Zorrilla
Cm
C
C
+
+
m+
m
Q0
Q0 ∗ A
Q0
∗A
∗
Q1
Q1 5 B
Q1
5B
5
C
C
Q2
Q
Q2
+
+
2+
D
D
Q3
Q
Q3
3 6
6
6
E
E
Q4
Q
Q4
412
12
12
F
Q 5 χ(K 5 ) = 5 F
Q5
χ(K 5 )Q=
5
χ(K
)
=
5
5
5
Q
0
G
G
χ(K
)
=
2
χ(K
)
=
2
χ(K
)
=
2
3,3
3,3
Abad 3,3
Abad
Abad
Q 1χ(C7 ) = 3Abascal
χ(C
7) = 3 H
Abascal χ(C7 ) = 3 H
Abascal
χ(esto)
=4 I
χ(esto) = 4Álvarez
Álvarezχ(esto) = 4 I
Álvarez
J
J
χ(esto
otro)
=
4
χ(esto
otro)
=
4
χ(esto
otro) = Bastardo
4
Bastardo
Bastardo
3
3
Cobas
Cobas
Cobas
+
(a) Cazorla +
(b)
Cazorla
Cazorla (c)
∗
Dehesa
Dehesa ∗
Dehesa
5
González
González 5
González
+
Guzmán
Guzmán +
Guzmán
6
Herrero
Herrero 6
Herrero
12
Lebrel
Lebrel 12
Lebrel
53
χ(K 5 ) = 5
Zapatero χ(K 5 ) = Q
Zapatero
Zapatero
χ(K 3,3 ) = 2
χ(K 3,3 ) = 2
Zorrilla
Zorrilla
Zorrilla
χ(C7 ) = 3
χ(C7 ) = 3
A
A
A
χ(esto) = 4
χ(esto) = 4
B
B
B
χ(esto otro) = 4
χ(esto otro) = 4 Q 4
C
C
C
D
D
D
(d)
(e)
E
E
E
F
F
F
Figura 1.7:
G
G Grafos Q n , para n = 0, . . . ,G4
H
H
H
I
I
I
J
J
J
3
3
3
+
+
+
∗
∗
∗
5
5
5
+
+
+
6
6
6
12
12
12
χ(K 5 ) = 5
χ(K 5 ) = 5
χ(K 5 ) = 5
χ(K 3,3 ) = 2
χ(K 3,3 ) = 2
χ(K 3,3 ) = 2
χ(C7 ) = 3
χ(C7 ) = 3
χ(C7 ) = 3
χ(esto) = 4
χ(esto) = 4
χ(esto) = 4
χ(esto otro) = 4
χ(esto otro) = 4
χ(esto otro) = 4
(a)
(b)
Q2
(c)
Figura 1.8: (a) Un árbol. (b) Un bosque. (c) Un grafo que no es ni un árbol ni un bosque
15
La figura 1.8(a) muestra un árbol, y en 1.8(b) vemos un bosque que no es un árbol,
al no ser conexo. El grafo de 1.8(c) no es un árbol ni un bosque, pues contiene un ciclo.
Antes de demostrar un importante teorema sobre árboles precisamos los dos lemas
siguientes, cuyas demostraciones son prácticamente idénticas.
Lema 1 Sea G un grafo no dirigido con n vértices y e aristas. Si G es conexo, se
verifica que e ≥ n − 1.
D EMOSTRACIÓN Por inducción sobre el número de vértices. El teorema es trivialmente
cierto para n = 1. Supongamos entonces que la desigualdad se verifica en todos los
grafos conexos con menos de n vértices.
Consideremos un vértice cualquiera v ∈ V (G) de grado d como el que mostramos en la figura 1.9, siendo sus vértices adyacentes v1 , v2 , . . . , vd . El grafo G − v
obtenido al suprimir v y sus aristas adyacentes posee n − 1 vértices, e − d aristas y
es posiblemente inconexo; al suprimir v, G puede divirse a lo sumo en d componentes conexas (¿por qué?). Sean entonces esas componentes los subgrafos C i de G, con
i = 1, 2, . . . , m ≤ d.
Cada componente C i es un grafo conexo con menos de n vértices. Por tanto, por
hipótesis de inducción, sus números de vértices n i y aristas ei satisfacen la desigualdad
ei ≥ n i − 1
i = 1, 2, . . . m
Sumando estas desigualdades sobre todas las componentes
!
m
m
m
X
X
X
ni − m
(n i − 1) =
ei ≥
i=1
i=1
i=1
Ahora, el primer sumatorio es el número de aristas de G − v, es decir, e − d, y el último
es el de vértices, n − 1. Como el número de componentes m no supera el grado d
e−d ≥n−1−m
e ≥n−1+d −m ≥n−1
es decir
como se quería demostrar.
El lema dual del recién probado cambia la conexión por la aciclicidad, con lo que
el sentido de la desigualdad se invierte.
Lema 2 Sea G un grafo no dirigido con n vértices y e aristas. Si G es acíclico, e ≤
n − 1.
D EMOSTRACIÓN Por inducción sobre el número de vértices. El teorema es trivialmente
cierto para n = 1. Supongamos entonces que la desigualdad se verifica en todos los
grafos acíclicos con menos de n vértices.
Consideremos un vértice cualquiera v ∈ V (G) de grado d como el que mostramos
en la figura 1.9, siendo sus vértices adyacentes v1 , v2 , . . . , vd . Al suprimir el vértice v
y obtener G − v, resulta ahora un grafo acíclico que, a diferencia del lema anterior,
posee al menos d componentes conexas (¿por qué?). Es decir, m ≥ d.
Ahora cada componente es un subgrafo acíclico y, por hipótesis de inducción
ei ≤ n i − 1
Sumando
m
X
i=1
ei ≤
m
X
i = 1, 2, . . . m
(n i − 1) =
m
X
i=1
i=1
16
ni
!
−m
Lebrel
Zapatero
Zorrilla
A
B
C
D
E
F
G
H
vd
I
C
m
J
3
..
+
.
∗C4
5
v
+ 6
6
12
χ(K 5 ) = 5
χ(K 3,3 ) = 2
v5
χ(C7 ) = 3
χ(esto) = 4
χ(esto otro) = 4
C3
v1
C1
v2
v
v3
C2
v4
Figura 1.9: Demostración de los lemas 1 y 2
En el presente caso, rige la desigualdad m ≥ d y se tiene entonces
e−d ≤n−1−m
es decir
e ≥n−1+d −m ≤n−1
como se quería demostrar.
Existen numerosas formulaciones equivalentes de la definición de árbol; el teorema
siguiente resume las fundamentales.
Teorema 4 Sea G = (V, E) un grafo no dirigido. Las siguientes afirmaciones son
equivalentes.
1.
G es un árbol
2. Dos vértices cualesquiera de G están conectados por un único camino simple
3.
G es conexo, pero si se le suprime una arista cualquiera, deja de serlo.
4.
G es conexo y |E| = |V | − 1
5.
G es acíclico y |E| = |V | − 1
6.
G es acíclico, pero si se le añade una arista, deja de serlo
D EMOSTRACIÓN 1 ⇒ 2) Sean u, v ∈ V . Como G es conexo, existe un camino simple
entre ellos. Si existen dos caminos simples distintos entre ambos vértices, se dará la
situación de la figura 4: los caminos p y p 0 divergen por primera vez en el vértice w
y vuelven a converger en el vértice z, pasando por vértices diferentes x e y. Como
resultado, es posible construir un ciclo, contra la hipótesis. Por tanto, no pueden existir
dos caminos simples distintos entre u y v.
2 ⇒ 3) Evidentemente, G es conexo. Si se suprime la arista (u, v) de G, los vértices
u y v quedan desconectados, pues, por hipótesis, dicha arista era el único camino simple
que los conectaba.
3 ⇒ 4) Una vez más, la conexión de G es parte de la hipótesis. Por otro lado, G
es acíclico, puesto que si tuviese un ciclo, podría suprimírsele una arista sin perder la
conexión. Por tanto, de los lemas precedentes de deduce que |E| = |V | − 1.
17
Álvarez
E
Bastardo
F
Cobas
G
Cazorla
H
DehesaI
González
J
Guzmán
3
Herrero
+
Lebrel
∗
Zapatero
5
Zorrilla
+
p
A6
x
v
B
12
u
χ(K 5 ) =C5
w
z
χ(K 3,3 ) =D2
χ(C7 ) = E3
y
χ(esto) = F4
0
p
χ(esto otro) =G4
H
Figura I1.10: Demostración de la implicación 1 ⇒ 2 en el teorema 4
J
3
7
+
∗
6
8
9
5
+
6
12
3
4
5
10
11
12
χ(K 5 ) = 5
χ(K 3,3 ) = 2
χ(C7 ) = 3
χ(esto) = 4
2
χ(esto otro) = 4 1
Figura 1.11: Arbol de doce nodos enraizado en el nodo 7
4 ⇒ 5) Si suprimimos una arista de G, deja de verificarse la desigualdad |E| ≥
|V | − 1; por tanto, de la implicación anterior se sigue que G es acíclico. La igualdad |E| = |V | − 1 es parte de la hipótesis.
5 ⇒ 6) Al añadir una arista a G, se viola la desigualdad |E| ≤ |V | − 1 y el
contrarrecíproco del lema 2 implica que G deja de ser acíclico.
6 ⇒ 1) Sean u y v dos vértices distintos de G (si no los hay la implicación es
trivial). Si existe una arista (u, v), los dos vértices son mutuamente accesibles; si no, la
adición de (u, v) a E(G) provoca la aparición de un ciclo C del que dicha arista es obviamente miembro. Suprimiendo (u, v) de C obtenemos un camino que conecta u y v.
1.6.1. Arboles enraizados
Un árbol enraizado es un árbol en el que marcamos uno de los vértices como
vértices disinguido. Dicho vértice se denomina raíz del árbol. Por ejemplo, el árbol de
la figura 1.11 tiene por raíz el nodo 7. Como puede verse, en los árboles enraizados es
más común llamar nodos a los vértices
Consideremos un nodo cualquiera v de un árbol enraizado de raíz r . Existe un único
camino entre r y v; cualquier nodo presente en ese camino es un ancestro o antecesor
de v. Si w es un ancestro de v, decimos que v es un descendiente de w. Todo nodo
es, por definición, ancestro de sí mismo; un ancestro de v diferente a él es un ancestro
propio. Un descendiente propio se define de forma análoga.
El subárbol con raíz en v es el subárbol inducido por los descendientes de dicho
vértice.
18
Lebrel
A
B
C
D
E
F
G
Abad
H
I
J
Álvarez
Zapatero
Abascal
3
+
∗
5
+
Guzmán
Bastardo González
6
12
χ(K 5 ) = 5
χ(K 3,3 ) = 2
χ(C7 ) = 3
Herrero
Dehesa
χ(esto) = 4 Cazorla
Cobas
χ(esto otro) = 4
Zorrilla
Figura 1.12: Buscando al abonado Dehesa
Supongamos que la última arista del (único) camino entre la raíz y un nodo v
es (w, v). En ese caso, decimos que w es el padre de v, y que v es hijo de w. Dos
nodos que tienen el mismo padre son hermanos. Un nodo sin hijos es una hoja o nodo
externo; en caso contrario, es un nodo interno. El número de hijos de un nodo es su
grado; obsérvese que, en este contexto, el grado de un nodo es una unidad inferior a lo
definido en la sección 1.2.2. Si todos los nodos de un árbol tienen grado a lo sumo m,
el árbol es m-ario. Así, en un árbol ternario cada nodo tiene, a lo sumo, tres hijos;
posiblemente, menos.
Definimos la profundidad de un nodo v como la longitud del camino de la raíz a v.
La altura de un árbol es el máximo de las profundidades de sus nodos. El árbol de la
figura 1.11 tiene altura 3, puesto que los nodos 1 y 2 tienen ambos dicha profundidad.
El subárbol con raíz en el nodo 9 tiene altura uno.
Un árbol enraizado en el que los hijos de cada nodo tienen asignado un orden es
un árbol ordenado. Esto significa que si un nodo tiene k hijos, hay un primer, segundo,
. . . , k-ésimo hijo.
El interés de los árboles reside en su uso como estructuras de datos para clasificar
información. Por ejemplo, el árbol de la figura 1.6.1 codifica un índice de una base de
datos de abonados telefónicos. El árbol es ordenado y cuaternario; tiene, además, la
propiedad de que los datos residentes en una rama son siempre anteriores a los datos
que residen en ramas situadas a su derecha. Esto lo convierte en un árbol de búsqueda.
Para localizar al abonado Dehesa, es suficiente encontrar qué hijo del nodo raíz lo
contiene, lo que se determina de inmediato. Prosiguiendo recursivamente de esta forma,
llegamos a encontrar al abonado en un número de pasos igual, a lo sumo, a la altura del
árbol de búsqueda.
¿Cuál podría ser esa altura en el caso de tener un millón de abonados?
Teorema 5 Sea T un árbol m-ario de altura h. Entonces, el número de nodos n del
árbol satisface la desigualdad
m h+1 − 1
n≤
m−1
19
Dicho de otro modo, un árbol m-ario de n nodos tiene que tener altura mínima dada
por
h ≥ −1 + logm ((m − 1)n + 1)
En particular, un árbol binario satisface las desigualdades siguientes
n
h
≤ 2h+1 − 1
≥ −1 + log2 (n + 1)
D EMOSTRACIÓN Si cada nodo tiene a lo sumo m hijos, habrá a lo sumo un nodo de
nivel 0 (el nodo raíz); m nodos de nivel 1 (sus hijos); m 2 nodos de nivel 2 (sus nietos);
m 3 nodos de nivel 3 (sus bisnietos); y, en general, el nivel k tendrá una población
máxima de m k nodos. Por lo tanto, el número total de nodos será inferior a
1 + m + m2 + m3 + · · · + mh =
m h+1 − 1
m−1
que es lo que se quería demostrar. Las demás desigualdades se obtienen despejando la
altura y particularizando para m = 2.
Como ejemplo, en el caso de un millón de abonados, tendríamos un árbol de altura
mínima
h ≥ −1 + log4 (3·106 + 1) = 9,758
luego un árbol de altura h = 10 podría albergar nuestro millón de abonados, si está correctamente equilibrado. En esta hipótesis, nuestra búsqueda concluiría tras la lectura
de once registros de nuestra base de datos a lo sumo, lo que no está nada mal.
1.6.2. Arboles binarios
Aunque podríamos definir estos árboles a partir de lo estudiado en las secciones
anteriores, seguiremos otra vía mucho más conveniente. Un árbol binario T es una
estructura definida en un conjunto finito de nodos, que, o bien
no contiene nodos, o bien
contiene tres conjuntos distintos de nodos: un nodo raíz, un árbol binario llamado
el subárbol izquierdo y otro llamado el subárbol derecho.
Observemos que está permitido que un árbol binario sea vacío: se trata del árbol
vacío o árbol nulo. Dado un árbol binario de raíz r , si el subárbol izquierdo no es
vacío, su raíz es el hijo izquierdo de r ; el hijo derecho de define análogamente. Es
posible, pues, que un hijo izquierdo o derecho estén ausentes (cuando sea vacío el
correspondiente subárbol).
Es preciso hacer notar que un árbol binario no es simplemente un árbol ordenado en
que cada nodo tiene a lo sumo dos hijos. En tal caso, no podríamos decidir, para un nodo
con un solo hijo, si éste es el izquierdo o el derecho. El árbol binario, pues, proporciona
“más estructura” que un simple árbol ordenado. Un nodo puede tener solamente un hijo
izquierdo o solamente un hijo derecho.
1.7. Recorridos de grafos
Un recorrido de un grafo es un procedimiento que origina una enumeración ordenada de sus vértices. Comenzaremos nuestro estudio de los recorridos por el caso
particular de los árboles binarios
20
P REORDEN(T )
1 if T = NIL
2
then no hacer nada
3
else V ISITA(T )
4
P REORDEN (T.i z)
5
P REORDEN (T.de)
P OSTORDEN(T )
1 if T = NIL
2
then no hacer nada
3
else P OSTORDEN(T.i z)
4
P OSTORDEN(T.de)
5
V ISITA(T )
I NORDEN(T )
1 if T = NIL
2
then no hacer nada
3
else I NORDEN(T.i z)
4
V ISITA(T )
5
I NORDEN(T.de)
Figura 1.13: Pseudocódigo de los recorridos de un árbol binario
1.7.1. Recorridos de árboles binarios
Recordemos que un árbol binario se define como
un grafo vacío, o bien
un nodo raíz más dos árboles binarios que constituyen el subárbol izquierdo y el
derecho
Esta definición recursiva es de especial interés cuando recorremos el árbol. Podemos definir tres maneras de visitar todos y cada uno de los vértices según se ve en la
figura 1.13. Aplicando estos procedimientos al árbol de la figura 1.14(a), se obtienen
las secuencias que se muestran en la tabla adjunta 1.14(b).
Estos tres tipos de recorrido se relacionan con tres notaciones usuales para las expresiones algebraicas
infija La notación del álgebra corriente exige que los operadores vayan en medio de
sus dos operandos. Por ejemplo, la expresión
3 + 5 ∗ (6 + 12)
está en notación infija.
postfija Se obtiene colocando cada operador binario a continuación de sus operandos. Al contrario que la infija, no requiere paréntesis ni reglas de precedencia
para resolución de la ambigüedad. La expresión anterior, en notación posfija se
convierte en
3 5 6 12 + ∗+
La notación postfija (también llamada polaca inversa es muy adecuada para su
interpretación por máquinas, lo que no es de extrañar a la luz del ejemplo anterior. Es muy sencillo escribir un programa que interprete de forma directa expresiones postfijas empleando una pila como estructura de datos auxiliar
pretfija Se obtiene colocando los operadores binarios como prefijos de los operandos.
Así:
+ 3 ∗ 5 + 6 12
No es de mucho uso, pero aún pervive en el lenguaje Lisp, donde el cálculo
anterior se escribiría como
(+ 3 (* 5 (+ 6 12)))
21
Zorrilla
A
B
C
D
E
F
G
H
I
J
3
+
∗
5
+
6
12
χ(K 5 ) = 5
χ(K 3,3 ) = 2
χ(C7 ) = 3
χ(esto) = 4
χ(esto otro) = 4
e
a
g
c
j
b
f
h
d
(a) Árbol binario
Tipo
Inorden
Preorden
Postorden
c
e
c
a
a
b
b
c
a
Resultado
e j g h
b g j f
j h d f
f
h
g
d
d
e
(b) Recorridos
Figura 1.14: Recorridos de un árbol binario
a pesar de que tampoco son precisos paréntesis ni reglas de precedencia para
resolución de ambigüedades (el uso de paréntesis en Lisp tiene un significado
distinto).
Las tres notaciones resultan de recorrer en in-, pre- y postorden un árbol sintáctico
de la expresión, como puede comprobarse en la figura 1.7.1.
1.7.2. Recorridos eulerianos
El problema que estudiamos a continuación se encuentra en el origen mismo de la
teoría de grafos y de otra importante rama de la Matemática: la topología. Se trata del
célebre problema de los puentes de Königsberg.
La ciudad de Königsberg, capital de Prusia y patria del célebre filósofo Immanuel
Kant, es atravesada por el río Pregel. En medio del río encontramos dos islas que se
encuentran comunicadas con las orillas y entre sí por siete puentes, como se muestra
en la figura 1.16.
Los habitantes de Königsberg se plantearon si era posible dar un paseo que recorriese los siete puentes sin repetir ninguno (y, naturalmente, sin mojarse). Tras numerosos
intentos infructuosos, la solución de este divertido problema combinatorio fue aportada por el matemático suizo Leonhard Euler en 1736. Euler no solamente demostró la
imposibilidad del pretendido paseo, sino que, además, dio un sencillo criterio general
para resolver cualquier problema del mismo tipo.
Si prescindimos de detalles anecdóticos, es fácil ver que la búsqueda de un paseo
por los puentes equivale a encontrar un camino que recorra todas las aristas del grafo
de la figura 1.17 sin repetir ninguna (naturalmente, los vértices pueden repetirse). O,
22
Zapatero
Cm
2
Q0
3
Zorrilla
Q1
4
A
Q2
6
B
Q3
9
C
Q4
12
D
Q5
18
E
36
F Abad
C1
G Abascal
C2
H Álvarez
C3
IBastardo
C4
J Cobas
C5
Cazorla
C7
+ Dehesa +
P6
González
Cm
Recorrido
Expresión
Guzmán
∗ Q0
3
Inorden
3 + 5 ∗ 6 + 12
Herrero
Q1
Postorden
3 5 6 12 + ∗+
Lebrel
Zapatero
Q2
Preorden
+3 ∗ 5 + 6 12
Q3
χ(K 5 ) = 5 Zorrilla
5
χ(K 3,3 ) = 2
Q4 +
Q5
χ(C7 ) = 3
χ(esto) = 4
Abad
12
6
χ(esto otro) = 4
Abascal
Álvarez
E
(a)
(b)
Bastardo
F
Cobas
G
Cazorla
H
Figura 1.15: a) Árbol sintáctico y b) notaciones infija, prefija y postfija para la expresión
Dehesa
I
3 + 5 ∗ (6 + 12)
González
J
Guzmán
3
+
Herrero
Lebrel
∗
ZapateroB
5
+
Zorrilla
6
12
χ(K 5 ) = 5
A
D
χ(K 3,3 ) = 2
χ(C7 ) = 3
E
χ(esto) = 4
F
χ(esto otro) = 4
G C
H
FiguraI 1.16: Los puentes de Königsberg
J
3
+
A
∗
5
+
6
12
D
χ(K 5 ) = 5B
χ(K 3,3 ) = 2
χ(C7 ) = 3
χ(esto) = 4
χ(esto otro) = 4 C
Figura 1.17: Los puentes de Königsberg
23
como suele formularse en las revistas de matemática recreativa, dibujar la figura de un
solo trazo sin levantar el lápiz del papel.
Sea G un grafo no dirigido. Denominamos recorrido euleriano de G a un camino que pasa por todas las aristas de G exactamente una vez. Es decir, si C =
(v1 , v2 , . . . , vn ), la sucesión de aristas (v1 , v2 ), (v2 , v3 ), (v3 , v4 ), . . . , (vn−1 , vn ) contiene cada arista de G exactamente una vez. Si además C es cerrado, denominamos al
recorrido un circuito euleriano
El grafo del problema de los puentes no es un grafo dirigido en el sentido de la
definición dada en 1.2.1, sino un multigrafo, en el que permitimos que haya más de
una arista distinta entre dos vértices. Aunque no hemos definido rigurosamente estos
objetos, todo lo que probaremos en la presente sección se extiende a ellos sin dificultad.
Decimos que un grafo es euleriano si posee un recorrido euleriano. Obviamente,
un grafo euleriano tiene que ser conexo. Pero, además, se necesitarán condiciones adicionales para garantizar la existencia de recorridos eulerianos. Tras bastantes ensayos
con el grafo de los puentes, parece claro que no podemos encontrar una solución.
La razón está en la paridad de los vértices del grafo. Decimos que un vértice v de
un grafo no dirigido G es par (respectivamente, impar) si su grado es un entero par
(resp. impar). Por ejemplo, en el grafo de la figura 1.17, todos los vértices son impares.
Ahora bien, si intentamos dibujarlo de un solo trazo, cada vez que pasemos por un vértice, entraremos en él por una arista y saldremos por otra; ambas quedarán inutilizadas
para su recorrido posterior. Excepto los vértices inicial o final de la trayectoria, todos
los demás (vértices de paso) tendrán tantas aristas de entrada como de salida; por tanto,
un número par de ellas, y su grado será par. Esto nos lleva al teorema de Euler.
Teorema 6 Sea G un grafo conexo no dirigido. Entonces, G posee un circuito euleriano si y solamente si G carece de vértices impares.
D EMOSTRACIÓN
Supongamos primero que G posee un circuito euleriano dado por la sucesión de
vértices C = (v0 , v1 , v2 , . . . , vn ). Por definición, cada arista del grafo aparece en la
sucesión (v0 , v1 ), . . . , (vn−1 , vn ) exactamente una vez, y al ser el recorrido cerrado,
v0 = v n .
Sea v un vértice cualquiera de G. Si v es el único vértice de G, no hay nada que
demostrar. Si no es así, v tendrá alguna arista incidente puesto que G se supone conexo,
y esto obliga a que v aparezca cierto número de veces en el camino C.
En cada aparición de v, éste figura dos veces; si, por ejemplo, está en la posición
k-ésima de C, v = vk y tenemos dos aristas (vk−1 , vk ) y (vk , vk+1 ) incidentes en vk .
Como estas aristas solamente figuran una vez en el recorrido, obtenemos que el número
de aristas incidentes en v es igual al doble del número de apariciones de v en C, y, como
todas las aristas son visitadas por C, el grado de v es forzosamente un número par.
La única excepción de este argumento se encuentra en los extremos: cuando k =
0, n, las dos aristas (vn , v0 ) y (v0 , v1 ) se añaden al recuento de aristas incidentes en v0
según el argumento anterior, de modo que también v0 = vn debe ser par.
La implicación contraria se demuestra por inducción sobre el número de vértices.
De hecho, vamos a demostrar esta implicación para multigrafos dirigidos.
Supongamos que G es un multigrafo conexo todos cuyos vértices son de grado par.
En el caso de un grafo de un solo vértice, el circuito euleriano se obtiene de forma
trivial. Así pues, sea |V | = n y supongamos que todo multigrafo conexo de menos
de n vértices, todos pares, posee un circuito euleriano.
Sea v un vértice cualquiera de G; por hipótesis de conexión, el grado d de v debe ser
un número par estrictamente mayor que cero. Consideremos los vérticesi v 1 , v2 , . . . , vd
24
Cobas
Cazorla
Dehesa
González
Guzmán
Herrero
Lebrel
Zapatero
Zorrilla
A
B
C
D
E
F
G
H
I
J
3
+
∗
5
+
6
12
χ(K 5 ) = 5
χ(K 3,3 ) = 2
χ(C7 ) = 3
χ(esto) = 4
χ(esto otro) = 4
C3
Cobas
C4
Cazorla
C5
Dehesa
C7
González
P6
Guzmán
Cm
Herrero
Q0
Lebrel
Q1
Zapatero
Q2
Zorrilla
Q3
A
Q4
B
Q5
C
Abad
D
Abascal
E
Álvarez
F
Bastardo
G
Cobas
H
Cazorla
I
Dehesa
J
González
v1
3
vd
Guzmán
+
Herrero
∗
Lebrel
v2
5
Zapatero
+
..
v Zorrilla
6
.
A
12
B
χ(K 5 ) = 5
v3
C
χ(K 3,3 ) = 2
D
χ(C7 ) = 3
E
v5
χ(esto) = 4
v4 F
χ(esto otro) = 4
G
(a) H
I
J
v1
3
vd
+
∗
5
+
v
6 ..
.
12
χ(K 5 ) = 5
χ(K 3,3 ) = 2
χ(C7 ) = 3
χ(esto) = 4 v5
v4
χ(esto otro) = 4
v1
vd
v2
..
.
v
v3
v5
v4
(b)
v2
v3
(c)
Figura 1.18: Demostración del teorema de Euler: (a) antes de suprimir v. (b) Suprimido v y añadidas las aristas auxiliares, el grafo resultante posee un circuito euleriano.
(c) Construcción del circuito euleriano para G
25
adyacentes a v, como se muestran en la figura 1.18(a). Si suprimimos v y las aristas
incidentes en él, obtenemos el grafo G − v; la supresión de las aristas indicadas se
muestra en gris en la figura 1.18(b). Ahora, los vértices vi resultan ser todos impares
tras la supresión. Adjuntando las aristas (v1 , v2 ), (v3 , v4 ), . . . , (vd−1 , vd ) obtenemos
un nuevo grafo en el que todos los vértices vuelven a ser de grado par; no obstante,
el número de vértices es ahora n − 1. Además, el nuevo grafo es obviamente conexo
(obsérvese que, por la adjunción de las nuevas aristas, podemos obtener un multigrafo).
Por lo tanto, se aplica la hipótesis de inducción, y deducimos que existe un recorrido
euleriano. El paso por las aristas auxiliares de dicho circuito se produce en sentidos
imprevisibles que indicamos con flechas en 1.18(b).
Queda convertir este circuito euleriano en uno para G. Para ello, basta observar que la nueva arista (vi−1 , vi ) siempre puede ser reemplazada por el recorrido de
(vi−1 , v), (v, vi ) (y en sentido contrario si es necesario), como se muestra en la figura 1.18(c). Con esto obtenemos un circuito euleriano de G y el teorema queda demostrado.
De este teorema se deduce un interesante corolario.
Corolario 1 Sea G un grafo conexo no dirigido. Si G tiene exactamente dos vértices
impares, G posee un recorrido euleriano. Recíprocamente, si G posee un recorrido euleriano, sus vértices extremos son los únicos vértices impares de G (si son diferentes).
D EMOSTRACIÓN Sean v y w los vértices impares en cuestión, y añadamos a G la
arista (v, w) (observemos que, una vez más, de esta adjunción puede resultar un multigrafo). Con esto, obtenemos un grafo en las hipótesis del teorema anterior, que posee
un circuito euleriano. Forzosamente, el circuito para por la arista (v, w) exactamente
una vez. Suprimiéndola del circuito obtenemos un recorrido del grafo G. Recíprocamente, un recorrido euleriano de vértices extremos v y w se completa, añadiendo la
arista (v, w), obteniendo un circuito euleriano del multigrafo resultante. Por lo tanto,
éste tiene todos sus vértices pares, de lo que se deduce que los vértices v y w eran
impares al principio.
Por lo tanto, un grafo tiene un recorrido euleriano si y solamente si el número de
vértices impares es cero o dos. Que dicho número no pueda ser la unidad es consecuencia del siguiente
Teorema 7 Sea G un grafo no dirigido. El número de vértices impares de G es siempre
par.
D EMOSTRACIÓN Sean {v1 , v2 , . . . , vn } los vértices de G y d1 , d2 , . . . , dn sus respectivos grados. El número de extremos que poseen las aristas de G es, evidentemente, 2|A|,
puesto que cada arista tiene dos extremos. Ahora bien, podemos contar dicho número
de extremos sumando los grados de todos los vértices, puesto que dichos grados son el
número de extremos de aristas que confluyen en un vértice dado. De modo que se tiene
n
X
di = 2|A|
i=1
Ahora bien, esto significa que la suma de los grados de los vértices es par. Como la
suma de dos números impares es siempre par, el número de d i0 s no puede ser impar,
puesto que el resultado de la suma sería impar en ese caso. Por tanto, hay un número
par de vértices impares.
26
B
C
D
E
F
G
H
I
J
3
+
∗
5
+
6
12
χ(K 5 ) = 5
χ(K 3,3 ) = 2
χ(C7 ) = 3
χ(esto) = 4
χ(esto otro) = 4
Figura 1.19: El puzzle de Hamilton
Es decir, un grafo nunca podrá tener un solo vértice impar (ni tres, ni cinco. . . ). Este
teorema se conoce a veces como “lema del apretón de manos”, porque puede ponerse
en la siguiente forma: en una fiesta, el número de personas que estrechan la mano a una
cantidad impar de gente tiene que ser necesariamente par. Es una consecuencia directa
de que en un apretón siempre intervienen dos manos.
1.7.3. Caminos hamiltonianos
Un problema de enunciado análogo, pero cuya simplicidad es tremendamente engañosa, es la determinación de si un grafo posee un camino hamiltoniano.
Sea G un grafo (dirigido o no). Un camino C en G se dice que es hamiltoniano si
C pasa por cada vértices del grafo exactamente una vez. Un ciclo que pasa exactamente
una vez por cada vértice (excepto el vértice inicial, que aparece también como final),
se denomina ciclo hamiltoniano
Al contrario que en el caso euleriano, aquí no precisamos recorrer todas las aristas; simplemente nos interesa visitar cada vértice exactamente una vez. Aunque no se
menciona explícitamente, los caminos hamiltonianos son siempre simples, lo que se
deduce directamente de la definición.
El nombre de este tipo de recorrido deriva de un puzzle ideado por Sir William
Rowan Hamilton (1805–1865). Básicamente, Hamilton pedía encontrar un ciclo hamiltoniano en un grafo isomorfo al retículo de vértices de un dodecaedro. La solución
es bastante sencilla. Sin embargo, dado un grafo arbitrario, no resulta fácil determinar
si posee un ciclo hamiltoniano o no.
De hecho, no se conoce ninguna caracterización fácil de los grafos hamiltonianos, y
es probable que nunca se conozca ninguna. La razón de ello es que el problema del ciclo
hamiltoniano es NP-completo. No es sencillo definir esta propiedad; baste mencionar
que una solución eficiente del problema del ciclo hamiltoniano permitiría resolver de
golpe una vasta familia de problemas computacionales enormemente difíciles, y existen
sospechas muy fundadas de que tal solución eficaz no puede existir.
Esto no implica que, para determinados grafos de tipos muy particulares, no sea posible determinar la existencia de caminos hamiltonianos (no necesariamente cerrados).
Un ejemplo de ello lo constituyen los torneos definidos en la sección 1.5.2.
Teorema 8 Todo torneo posee un camino hamiltoniano
D EMOSTRACIÓN Por inducción sobre el número de vértices n = |V |. El teorema es
trivial para n = 1.
27
B
C
D
E
F
G
H
I
J
3
+
∗
5
+ v2
6
12
χ(K 5 ) = 5
χ(K 3,3 ) = 2
χ(C7 ) = 3
χ(esto) = 4
χ(esto otro) = 4
vm
v3
vm+1
vn
v1
Figura 1.20: Construcción de un camino hamiltoniano en un torneo.
Consideremos entonces un torneo G de n vértices y supongamos que todo torneo
de n − 1 vértices posee un camino hamiltoniano. Sea v = v1 un vértice de G y consideremos el grafo G − v que se obtiene suprimiendo v y todas las aristas que entran
o salen de dicho vértice. El grafo resultante tiene n − 1 vértices y, por hipótesis de
inducción, posee un camino hamiltoniano. Sea éste C = (v2 , v3 , . . . , vn ); numeramos
los vértices en el orden que dicho camino nos proporciona, por conveniencia. Nuestra
notación implica, naturalmente, que el camino supuesto por hipótesis va de v 2 a vn , no
en sentido contrario.
Ahora pueden darse tres posibilidades:
1. El torneo posee una arista (v1 , v2 ). En ese caso, puede completarse el camino C
añadiéndole al principio esta arista y obteniéndose un camino hamiltoniano C 0 =
(v1 , v2 , . . . , vn ) para G, con lo que el teorema quedaría demostrado.
2. El torneo posee una arista (vn , v1 ). En ese caso, puede completarse el camino C
añadiéndole al final esta arista y obteniéndose un camino hamiltoniano C 0 =
(v2 , . . . , vn , v1 ) para G, con lo que el teorema quedaría demostrado.
3. Si ninguna de las circunstancias anteriores se da, la definición de torneo obliga
a que G posea las aristas (v2 , v1 ) y (v1 , vn ). Para cada vértice vk , con 2 ≤ k ≤
n, debe existir una arista ak con ak = (v1 , vk ) o ak = (vk , v1 ), puesto que
así lo exige el hecho de que G sea un torneo. Esta situación se describe en la
figura 1.7.3.
Consideremos entonces la sucesión de aristas a2 , a3 , a4 , . . . , an . En nuestro caso,
la primera arista entra en v1 y la última sale de v1 . Por lo tanto, tiene que haber
una última arista que entre en v1 en esa sucesión, antes de llegar a an . Sea dicha
arista am . Entonces, si reemplazamos la arista vm , vm+1 de C por el par de aristas
am y am+1 obtenemos
C 0 = (v2 , v3 , . . . , vm , v1 , vm+1 , vm+2 , . . . , vn )
que constituye el deseado camino hamiltoniano, y el teorema también es cierto
para G en este caso.
28
González
Guzmán
Herrero
Lebrel
Zapatero
Zorrilla
A
B
C
D
E
F
G 1
H
I
J
+ 4
∗
2
3
5
6
8
9
Vértice
1
2
3
4
5
6
7
8
9
10
+
12
χ(K 5 ) = 5
χ(K 3,3 ) = 2
χ(C7 ) = 3
χ(esto) = 4
χ(esto otro) = 4
7
Adyacentes
{2, 4}
{1, 3, 5}
{2, 5}
{1, 5, 7, 8}
{2, 3, 4, 6, 8, 9}
{5}
{4, 8, 10}
{4, 5, 7, 9, 10}
{5, 8}
{7, 8}
10
(a) Grafo ejemplo
(b) Lista de adyacencia
Figura 1.21: Datos de partida para recorridos en anchura y profundidad
1.7.4. Recorridos en anchura y profundidad
Los algoritmos clásicos de teoría de grafos se basan en dos procedimientos básicos de recorrido denominados recorrido en anchura (breadth-first) y recorrido en
profundidad (depth-first). Aunque admiten muchas formulaciones (por ejemplo, como algoritmos de búsqueda en árboles), aquí estableceremos su funcionamiento en el
caso de grafos no dirigidos; para otros contextos funcionan exactamente igual con las
modificaciones obvias.
Consideremos el grafo de la figura 1.21(a), en la cual mostramos además su representación por listas de adyacencia (1.21(b)). Vamos a enunciar y ejecutar dos algoritmos que producen una enumeración ordenada de cada vértice del árbol. En cada
algoritmo, procedemos visitando cada vértice y añadiendo sus vecinos a una lista de
vértices pendientes. La visita de un vértice consiste en marcarlo como visitado y, si
procede, tratar la información que contiene y emitir su nombre o algún otro dato como
resultado de la visita. Hecho esto, seguimos tratando los vértices que queden pendientes.
A grandes rasgos, los algoritmos de recorrido se describen en pseudocódigo en la
figura 1.22. El recorrido en profundidad admite una formulación recursiva muy simple, mientras que el recorrido en anchura debe formularse en términos de una cola
de vértices pendientes de visitar. En la cola, que inicialmente contiene sólo el vértice
de partida, los vértices se mantienen en orden; se extraen del principio con la operación S ACA P RIMERO y se añaden al final con la operación E NCOLA. Los vértices ya
visitados no se introducen en la cola en dicha operación.
En la tabla de la figura 1.23(a) podemos observar la operación del algoritmo de
recorrido en anchura. En cada paso, se toma el primer elemento de la cola, que se anota
como visitado, y se examina su lista de adyacencia. Los vecinos que no hayan sido
ya visitados se añaden al final de la cola antes de proceder a la siguiente iteración.
29
D EPTH -F IRST(G, v)
1 V ISITA (v)
2 for each w in Ad j (v)
3 do D EPTH -F IRST(G, w)
B READTH -F IRST(G, v)
1 Q ← [v]
2 while Q 6= ∅
3 do w ← S ACA P RIMERO (Q)
4
V ISITA(w)
5
E NCOLA(Ad j (w))
(a) En profundidad
(b) En anchura
D EPTH -F IRST-NR(G, v)
1 S ← vaci o
2 P USH (v)
3 while S 6= ∅
4 do w ← P OP(S)
5
if w no visitado
6
then
7
V ISITA(w)
8
next ← Ad j (w)
9
next ← next − V ISITADOS(next)
10
P USH(next)
11
(c) En profundidad, no recursivo
Figura 1.22: Recorridos en anchura (a) y en profundidad (b, c); pseudocódigos
Como resultado de este proceso, obtenemos que el recorrido construye un árbol como
el mostrado en 1.23(b). Cada nodo figura en este árbol como hijo del nodo “culpable”
de su ingreso en la cola Q. Un árbol de esta forma es un árbol abarcador (spanning
tree): cubre todos los vértices del grafo.
El recorrido de los vértices en profundidad es más difícil de visualizar al ser recursiva la formulación natural del algoritmo 1.22(a). La idea consiste en visitar en cada
paso cualquiera de los nodos vecinos aún no visitados, hasta que llegamos a un callejón
sin salida (es decir, no hay más vecinos inmediatos sin visitar). En ese caso es preciso
volver atrás y reiniciar nuestro paseo en el último punto en el que dejamos sin explorar
alguna posibilidad.
Una forma menos vaga de expresar este procedimiento es la forma no recursiva
del recorrido en profundidad que se esboza en el algoritmo de la figura 1.22(c). En
esta versión se emplea una pila S, en la que se almacenan los vértices pendientes de
ser recorridos. La operación de una pila es inversa a la de una cola: los elementos se
introducen en ella por delante (con la operación P USH) y se sacan de ella también del
principio (P OP).
Inicialmente introducimos en la pila sólo el vértice de partida. Mientras la pila no se
vacíe, tomamos el primer elemento de la pila (que es el último introducido, al revés que
en una cola); si no está marcado como visitado ya, lo visitamos; y finalmente apilamos
su lista de adyacentes (salvo los que estén marcados como visitados, que no se añaden).
30
Zapatero
Zorrilla
A
B
C
D
E
F
G
H
I
J
Visitados
–
1
12
124
1245
12453
124537
1245378
12453786
124537869
1 2 4 5 3 7 8 6 9 10
Cola Q
+
1
∗
23
453
+
5378
37869
12
7869
χ(K 5 ) = 5
8 6 9 10
χ(K 3,3 ) = 2
6 9 10
χ(C7 ) = 3
9 10
χ(esto) = 4
10
χ(esto otro) = 4
–
1
2
3
4
5
6
7
8
9
10
(b) Arbol abarcador
(a) Traza
Figura 1.23: Funcionamiento del algoritmo B READTH -F IRST: (a) Traza del algoritmo,
con la historia de vértices visitados y el estadode la cola en cada iteración, (b) árbol
abarcador resultante del recorrido
Un ejemplo de ejecución de este proceso aparece en la tabla de la figura 1.24(a),
donde vamos viendo la historia de los contenidos de la pila y los elementos que van
visitándose en sucesión. Como resultado del proceso obtenemos también el diagrama 1.24(b), que es otro árbol abarcador del grafo inicial. Una vez más, las aristas del
grafo relacionan cada vértice con el “culpable” de su inclusión en la pila de pendientes.
Las flechas grises indican los momentos en que se produjo vuelta atrás (backtracking)
al haberse encontrado un callejón sin salida.
1.7.5. Caminos mínimos, MST y demás
Los algoritmos de recorrido de la sección 1.7.4 son la base de los algoritmos clásicos de teoría de grafos que se estudian en la teoría de Estructuras de Datos y Algorítmica. De hecho, la estructura de datos básica subyacente a las búsquedas en anchura
y profundidad (cola o pila) puede reemplazarse por una estructura más general denominada cola de prioridad, en la que los elementos son recuperados de acuerdo con
un valor de prioridad que se asocia a cada uno. Con valores adecuados de la prioridad, se obtienen búsquedas en anchura, en profundidad o recorridos que conducen a
algoritmos para encontrar caminos mínimos o árboles abarcadores.
Estos conceptos se relacionan con el concepto de red. Una red se define como un
grafo a cada una de cuyas aristas se ha asociado un número real, denominado su peso
o coste. En la figura 1.25 tenemos un ejemplo de red. El coste asociado a un camino
se obtiene de la forma obvia: sumando los pesos de las aristas que lo componen, y lo
mismo puede definirse para un subárbol de la red correspondiente.
Se denomina camino mínimo (o camino más corto) entre dos vértices v y w al
camino de peso menor que une los dos vértices. En la red de la figura 1.25, el camino
más corto entre los vértices 1 y 8 es el marcado en línea de trazos. El algoritmo para
encontrar este tipo de caminos es el algoritmo de Dijkstra y se estudiará con profusión
en la asignatura de Estructuras de Datos.
31
Pila
1
24
2875
2872368
2 8 7 2 3 6 9 7 10
287236977
28723697
2872369
287236
28723
2872
287
28
2
Herrero
Lebrel
Zapatero
Zorrilla
A
B
C
D
E
F
G
H
I
J
Visitado
1
4
+
5
∗
8
10
+
7
–
12
9
χ(K 5 ) = 5
6 χ(K 3,3 ) = 2
3
χ(C7 ) = 3
2 χ(esto) = 4
–
χ(esto
otro) = 4
–
–
1
2
3
4
5
6
7
8
9
10
(b) Arbol abarcador
(a) Evolución del stack
Figura 1.24: Funcionamiento del algoritmo D EPTH -F IRST: (a) Traza del algoritmo,
con la historia de vértices visitados y el estado de la pila en cada iteración, (b) árbol
abarcador resultante del recorrido
. Las flechas grises indican los procesos de backtracking.
Las aristas marcadas con trazo grueso en la misma figura (de pesos 3, 6, 5, 13, 14,
17 y 25) constituyen un árbol abarcador mínimo (en inglés, minimum spanning tree
o MST. Se trata de un árbol que cubre todos los vértices del grafo teniendo el peso
menor posible. Existen dos algoritmos clásicos para encontrar tal MST, los algoritmos
de Kruskal y Prim; serán también objeto de estudio en el futuro.
32
Q0
Q1
Q2
Q3
Q4
Q5
Abad
Abascal
Álvarez
Bastardo
Cobas
Cazorla
Dehesa
González
Guzmán
Herrero
Lebrel
Zapatero
Zorrilla
A
B
C
D
E
F
G
H
I
J
2
+
∗
32
12
21
8
6
1
5
+
17
13
14
8
χ(K 5 ) = 5
χ(K 3,3 ) = 2
χ(C7 ) = 3
χ(esto) = 4
χ(esto otro) = 4
18
3
3
15
6
7
24
4
25
5
69
Figura 1.25: Una red con el camino más corto entre 1 y 8 y su MST
33
Cazorla
Dehesa
González
Guzmán
Herrero
Lebrel
Zapatero
Zorrilla
A
B
C
D
E
F1
G
H
I
J
2
2
1
2
1
2
3
1
3
2
1
3
4
2
1
1
χ(C7 ) = 3
χ(K 3,3 ) = 2
+
∗
+
61
12
2
2
1
4
5
χ(K 5 ) = 5
1
2
1
3
3
2
4
2
1
4
2
1
2
2
3
3
χ(esto) = 4
1
3
1
χ(esto otro) = 4
Figura 1.26: Algunos grafos y sus números cromáticos
1.8. Planaridad y coloreado
Se dice que un grafo G = (V, E) (simple, no dirigido y sin bucles) es coloreable con n colores, o simplemente n-coloreable, si existe una función f : V →
{1, 2, . . . , n} tal que si u y v son vértices adyacentes, f (u) 6= f (v). Intuitivamente,
esta definición implica que, disponiendo de n colores distintos, podemos colorear los
vértices del grafo de modo que los vértices vecinos se distingan por el color. El menor
número n de colores que resulta suficiente para colorear un grafo G se denomina su
número cromático, y se denota por χ(G).
En la figura 1.26 mostramos algunos ejemplos de grafos con diferentes números
cromáticos.
Vamos a dar algunos teoremas que nos permiten estimar un número de colores
suficiente para el coloreado de ciertos grafos
Teorema 9 Dado un grafo G, las siguientes afirmaciones son equivalentes: a) G es
2-coloreable, b) G es bipartito, y c) G carece de ciclos de longitud impar.
D EMOSTRACIÓN La equivalencia de b) y c) fue el contenido del teorema 3; nos queda,
pues, probar la (casi trivial) equivalencia de a) y b).
Si un grafo G admite un coloreado con dos colores, llamémoslo f : G → {1, 2},
denotemos
V1
= {v ∈ V (G) | f (v) = 1}
V2
= {v ∈ V (G) | f (v) = 2}
es decir, los conjuntos V1 y V2 contienen los vértices de color 1 y color 2, respectivamente. Obviamente, estos conjuntos forman una partición de los vértices de V . Al
34
ser f un 2-coloreado, vértices adyacentes tienen colores distintos: dicho de otro modo,
cada arista va de V1 a V2 , y el grafo es, por tanto, bipartito.
Si G es bipartito, con aristas entre dos conjuntos V1 y V2 exclusivamente, basta
asignar el primer color a los vértices de V1 y el segundo a los de V2 .
El caso de los grafos bipartitos es bastante especial. Un teorema algo más general,
aunque no demasiado potente, nos da una cota superior para el número de colores
preciso en un grafo cualquiera G.
Teorema 10 Si
1(G) = max {deg(v) | v ∈ V (G)}
es el mayor de los grados de los vértices de G, entonces
χ(G) ≤ 1(G)
Dicho de otra manera, si el vértice de mayor grado de G tiene grado d, bastan d + 1
colores para colorear G.
D EMOSTRACIÓN Por inducción sobre el número de vértices. Si el grafo tiene un
solo vértice, su grado será cero y el grafo es trivialmente 1-coloreable, o sea que
χ(G) = 1 ≤ 1 = 1(G) + 1
Supongamos ahora que G tiene un número cualquiera |V | de vértices, y que el teorema
que queremos probar es cierto para todos los grafos con menos vértices que |V |. Sea
v un vértice de máximo grado de G, i.e., deg(v) = 1(G). Suprimamos v y todas las
aristas en él incidentes, obteniendo el grafo G 0 = G − v. Evidentemente, G 0 tiene un
vértice menos, y está claro que 1(G 0 ) ≤ 1(G), así que G 0 es (1(G) + 1)-coloreable,
por hipótesis de inducción. Ahora bien, si consideramos un (1(G) + 1)-coloreado de
G 0 , podemos extenderlo a un coloreado de G asignando algún color a v. Como el grado
de v es 1(G), alguno de los 1(G) + 1 colores no se ha utilizado en teñir a los vecinos
de v, y ese color podrá utilizarse para teñir a v, con lo que también G será (1(G) + 1)coloreable.
Obsérvese que este teorema proporciona un número de colores suficiente, pero puede ser bastante mayor que el mínimo necesario. Por ejemplo, para K 3,3 (véase la figura 1.26) el teorema dice que cuatro colores bastan, y es así, porque de hecho bastan
dos. El caso del último grafo de la misma figura es especialmente significativo: hay un
vértice de grado 8, luego el teorema garantiza que nueve colores bastan. Sin embargo,
en la práctica vemos que con cuatro es posible colorear el grafo.
El último teorema sobre coloreado que veremos no se demostrará: sería realmente
difícil, por las razones que después veremos.
Definimos un grafo plano como uno que es factible representar en el plano de forma
que sus aristas no tengan intersecciones (salvo en los extremos, claro). Por ejemplo, la
figura 1.26 representa tres grafos planos. Los dos primeros no lo son: aunque no es
obvio, K 5 y K 3,3 son imposibles de dibujar en un plano sin que alguna arista se cruce
con otra.
Una propiedad curiosa de los grafos planos es la siguiente, que enunciamos sin
demostrar:
Teorema 11 Si G es un grafo plano, el número C de regiones conexas en que su representación divide al plano satisface la relación
C − A+V =2
siendo A y V los números de aristas y vértices, respectivamente.
35
El teorema al que hacíamos referencia antes es el
Teorema 12 (de los cuatro colores) Todo grafo plano es 4-coloreable
La interpretación geométrica de este enunciado es que cualquier mapa puede colorearse con cuatro colores de forma que países fronterizos se distingan por el color.
Por complejo que sea el mapa, cuatro colores serán siempre suficientes. El teorema
de los cuatro colores se demostró en 1976, tras más de un siglo de intentos fallidos y
la comprobación exhaustiva por computador de miles de configuraciones a las que la
demostración se reduce.
36