Estática.

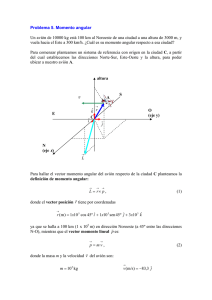
Estática.
Momento de un vector respecto de un punto: Momento de una fuerza
−→
Sea un vector genérico ~a = AB en un espacio vectorial V . Sea un punto cualesquiera O. Se define
~ del vector ~a respecto del punto O al producto vectorial
el vector momento M
~ = ~r ∧ ~a
M
−→
donde ~r = OA.
M
B
a=AB
O
r =OA
A
θ
Para una partícula moviéndose respecto O con vector de posición ~r y de que ~a sea la resultante de
todas las fuerzas que actúan sobre dicha partícula, es decir ~a = F~ ⇒
~ = ~r ∧ F~
M
es el momento o torque de la fuerza F~ con respecto a un punto O. En algunos libros se le
~ = 1N × m y en el sistema c.g.s
suele representar con la letra ~τ . Sus unidades en el S.I. son [M]
~ ] = 1dina × cm
[M
37
~ = |~r||F~ |senθ
Módulo |M|
Dirección perpendicular al plano que forman ~r y F~
Sentido, el que da la regla de la mano derecha, o la regla del tornillo (el sentido de avance de
un tornillo que gira de ~r a ~p por el camino más corto).
Momento de un sistema de fuerzas aplicadas en distintos puntos respecto de un punto O es la
suma de los momentos de cada una de las fuerzas respecto del mismo punto O
X
X
~ =
~i =
M
M
~ri ∧ F~i
i
i
El movimiento de rotación de un cuerpo es producido por el momento que tiene las fuerzas
que actúan sobre las partículas del cuerpo respecto del punto por el que pasa el eje de giro.
Ejemplo: el momento que hace la fuerza de rozamiento hace que las ruedas de los coches giren:
vcdm
Froz
v’3 =vcdm
3 vcdm
vcdm
2
4
vcdm
v’4
+
v3 =2v cdm
45 o
=
v2
v’2
1v
v’1 =−vcdm
cdm
38
v1 =0
v4
Una rueda gira sin deslizar cuando el punto de contacto de la rueda con el suelo tiene velocidad
~v ′ = −V~cdm
1
pero su módulo vi′ = ri′ ω = Rω por lo que la condición para que la rueda no deslice es que
Vcdm = Rω
Dinámica combinada de traslación y rotación
Movimiento más general de un cuerpo sometido a la acción de fuerzas actuando sobre diferentes
puntos del cuerpo se tienen que cumplir la segunda ley de Newton
X
F~i = M~acdm
i
o en módulo
F = Macdm
(5)
El índice i puede denotar las partículas que forma el sólido y siempre podremos descomponer
la fuerza neta como suma de fuerzas actuando sobre cada una de las partículas del sólido.
Si la resultante de esas fuerzas produce además un giro del cuerpo entorno a un eje O ⇒
X
~ =
M
~ri ∧ F~i
i
Descomponemos cada fuerza F~i en sus tres componentes una a lo largo del eje O otra a lo
largo del eje radial perpendicular a O y otra perpendicular a ambos y por lo tanto tangencial
al movimiento circular alrededor de O (ver dibujo), es decir que F~i = F~i,O + F~i,R + F~i,T y lo
mismo para ~ri = ~ri,O + ~ri,R
39
Fi
M
Fi,O
F i,T
O
ri,R=OA
A
F i,R
ri
~ en la dirección del eje de giro es
Se tiene entonces que la componente de M
X
~O =
M
~ri,R ∧ F~i,T
i
pero F~i,T = mi~ai,T , pero |~ai,T | = αi ri,R luego
X
~
MO =
mi αi (ri,R )2~uo = αI~uO
que como todas las partículas tienen la misa aceleración angular nos queda en módulo
MO = αI
(6)
que es el equivalente a la segunda ley de newton (5) y que junto a ella nos permite estudiar de
forma conjunta el movimiento de traslación y rotación alrededor de un eje siempre y cuando
dicho eje no cambie de dirección. De aquí se deriva que el momento de las fuerzas actuando
40
sobre el cuerpo es cero cuando la aceleración angular es nula, es decir el cuerpo gira
con velocidad angular constante, y que se conoce como segunda condición del equilibrio o
equilibrio de rotación.
Trabajo y potencia en el movimiento de rotación
En virtud del teorema de Koening vimos que para un cuerpo con movimiento de rotación y
traslación
1
1
2
Ec = MVcdm
+ Iω 2
2
2
donde I es el momento de inercia entorno a un eje que pasa por el centro de masas y ω la
velocidad angular de rotación. Si además el sólido rígido está sometido al campo gravitatorio
de la tierra y cambia su altura respecto a la superficie adquiere una energía potencial
Ep = Mgzcmd
Calculamos el trabajo realizado por las fuerzas que producen la rotación del sólido entorno a
O (es decir solo rotación). El trabajo elemental en rotar un arco ds = |d~l| por la fuerza F~i es
dWi = F~i · d~l
pero F~i = F~i,O + F~i,r + F~i,T de donde como d~l = ds ~uT se tiene
dWirot = Fi,T ds
para ángulos pequeños se tiene dθ ≈
ds
ri
lo que implica dWirot = Fi,T ri dθ es decir
dWirot = Mi dθ
41
y por lo tanto el trabajo elemental al rotar un ángulo dθ debido a todas las fuerzas es
X
dW rot =
dWirot = Mdθ
i
de donde
W
rot
=
Z
θ2
Mdθ
θ1
Si asumimos que M no cambia al variar el ángulo de rotación se tiene
W rot = M(θ2 − θ1) = M∆θ
que sería el trabajo realizado por un torque constante al rotar alrededor de un eje O un ángulo
∆θ. Esta equación es el análogo a W = F s en el movimiento de traslación. Si ahora ponemos
M = αI = dω
dt I tenemos que
dω
dW rot = Mdθ = I dθ = Iωdω
dt
de donde
Z ω2
1
1
Iωdω = Iω22 − Iω12 = Ecrot (2) − Ecrot (1)
W rot =
2
2
ω1
La potencia asociada a este trabajo es
dω
dW rot
rot
= Iω
= Iωα
P =
dt
dt
o también
dθ
P rot = M
= Mω
dt
que es el análogo a la relación para la potencia en el movimiento de traslación P = F~ · ~v
42
Vector momento angular
L
O
r
P
θ
p
Se define la magnitud vectorial momento angular o momento cinético de la partícula P
~ como
respecto del punto O y lo denotaremos por L
~ = ~r ∧ m~v = ~r ∧ p~
L
donde ~r es el vector de posición de la partícula respecto del punto O, ~v su velocidad y p~ su momento
~ en el S.I. son [L]
~ = 1Kg × m2 /seg y en el
lineal o cantidad de movimiento. Las unidades de L
~ = 1gr × cm2 /seg. El módulo dirección y sentido viene dado por la definición de
sistema (c.g.s) [L]
producto vectorial (ver dibujo)
~ = |~r||~p|senθ
Módulo |L|
Dirección perpendicular al plano que forman ~r y p~
Sentido, el que da la regla de la mano derecha, o la regla del tornillo, es decir sería el sentido
de avance de un tornillo que gira de ~r a ~p por el camino más corto.
43
~ es constante en el tiempo, pero sólo su dirección la dirección ⇒ la trayectoria de la
Si L
partícula es plana, está incluida siempre en el mismo plano (plano que forman ~r y p~). Si la
~ cambia.
partícula se sale de ese plano, la dirección de L
De las propiedades generales del producto vectorial
~i ~j
~ = rx ry
L
p p
x
y
de dos vectores se tiene
~k rz pz Nos preguntamos por cual es la varición del momento angular con el tiempo
~
dL
d~r
d~p
=
∧ p~ + ~r ∧
= ~v ∧ p~ + ~r ∧ F~
dt
dt
dt
El primer término es nulo pues ~v k p~ luego su producto vectorial es cero. El segundo término
es el momento de la resultante de las fuerzas que actúan sobre la partícula ⇒
~
dL
~
=M
dt
(7)
p
. Mientras F~ es la
Ecuación es análoga a la 2ª ley de Newton escrita en la forma F~ = d~
dt
~ define la dinámica de rotación.
magnitud que define la dinámica de traslación de un cuerpo, M
~ es constante entonces M
~ = 0 y esto puede ocurrir porque:
Consecuencia de (7) es que si L
• F~ = 0 (no hay fuerza neta actuando)
44
• ~r = 0 (el punto sobre el que aplica la fuerza pertenece al eje de giro)
• ~r y F~ tienen la misma dirección ⇒ p.e. en un campo de fuerzas centrales. Campo gravitatorio creado por el sol ⇒ el momento angular de los planetas girando alrededor del sol
es contante en módulo dirección y sentido ⇒ órbitas planas (ver dibujo)
F
F
O
F
r
F r
F r
F
r
• Lo anterior no es sino otra versión de la segunda condición del equilibrio o equilibrio de
rotación, “Si a un cuerpo que puede girar alrededor de un eje O, se la aplican varias fuerzas
~ = 0 entonces no se producen variación en su movimiento de rotación, se dice
tal que M
que el cuerpo puede estar en reposo o tener movimiento uniforme de rotación (velocidad
angular constante o aceleración angular cero).”
Para un sistema de n partículas, el momento angular del sistema respecto de un punto O es la
suma de los momentos angulares de cada una de ellas respecto del punto O
X
X
X
~ =
~i =
L
L
~ri ∧ mi~vi =
~ri ∧ p~i
(8)
i
i
i
Trivialmente se tiene que para un sistema de n partículas sometidas cada una a una fuerza
externa F~i , el momento total de todas esas fuerzas externas es
X
X dL
~
~i
dL
~
~
=
(9)
Mext =
~ri ∧ Fi =
dt
dt
i
i
45
~ = P ~ri ∧ p~i . De forma que si L
~ = cte entonces M
~ ext = 0 (Ley de conservación del
donde L
i
momento angular total del sistema de n partículas)
Estos resultados los podemos extender a un sólido o cuerpo rígido. la ecuación (8) en la forma
más general en función de sus componentes, en el caso de un sólido rígido es :
X
X
X
~i =
~ =
L
L
mi~ri ∧ ~vi =
mi~ri ∧ (~ω ∧ ~ri )
i
i
i
Nota: Se puede demostrar (Ejercicio) que dados tres vectores se tiene la propiedad
~a ∧ (~b ∧ ~c) = ~b(~a · ~c) − ~c(~a · ~b)
de donde para nuestro caso tenemos
P
~ =
L
ω (~ri · ~ri ) − ~ri (~ri · ω
~ )]
i mi [~
P
P
P
2
2
Lx = ωx Pi mi (ri − xi ) −Pωy i mi xiyi − ωz Pi mi xi zi
Ly = −ωx i mi yi xi + ωy i mi (ri2 − yi2 ) − ωz i mi yi zi
P
P
P
Lz = −ωx i mi zi xi − ωy i mi zi yi + ωz i mi (ri2 − zi2 )
que se puede poner en forma matricial como
 



Ixx Ixy Ixz
ωx
Lx
 Ly  =  Iyx Iyy Iyz   ωy 
Izx Izy Izz
ωz
Lz
que me define la matriz de inercia o tensor de inercia Iˆ de forma que
~ = Iˆ · ω
L
~
46
Si el movimiento es tal que ω
~ sólo tiene componente en la dirección del eje z (movimiento de
rotación entorno a un eje) , es decir ~ω = ω~kentonces
~ = Ixz ω~i + Iyz ω~j + Izz ω~k
L
es decir el vector momento angular tiene componentes en las tres direcciones del sistema de
referencia. Si el sólido tiene simetría de revolución alrededor del eje z ⇒ (EJERCICIO) que
Ixy = 0 e Iyz = 0 de donde
~ = Izz ω~k
L
P
P
P
2
pero Izz = i mi (ri2 − zi2 ) = i mi (x2i + yi2 ) = i mi (ri,R
) = I que antes lo hemos llamado
I = MO /α luego tenemos
~ = Iω~k
L
de donde derivando con el tiempo se tiene
~
dω
dL
= I ~k = Iα~k
dt
dt
e identificando ~k = ~uO tenemos el resultado
~
dL
~O
=M
dt
equivalente a la ecuación (9) para el movimiento de rotación de un sólido rígido con simetría
axial entorno a un eje O.
47
Pares de fuerzas
Se conoce como par de fuerzas a un sistema sobre el que actúan dos fuerzas del mismo módulo,
sentidos contrarios y la misma dirección sobre rectas paralelas (ver dibujo).
FA
FA
rA
FB
d
FA
rB
FB
FB
De las tres casos solo los dos primeros corresponderían a un par de fuerzas. Podemos calcular el
momento total producido por el par en las tres situaciones anteriores sobre un eje que pasa por el
centro de la circunferencia
~ =M
~A + M
~ B = ~rA ∧ F~A + ~rB ∧ F~B
M
~A
pero de la definición de producto vectorial (y usando la regla de la mano derecha) tenemos que M
~ B tienen la misma dirección y sentido, por lo que se cumple
yM
~ | = |M
~ A | + |M
~ B|
|M
~ A | = |~rA ||F~A | sinθ y |M
~ B | = |~rB ||F~B | senθ. Pero |~rA | = |~rB | = d/2 y|F~A | = |F~B | = F luego
con |M
se tiene
~ | = F d senθ
|M
~ | = Fd
Si θ = π/2 (primer caso) |M
48
~|=0
Si θ = π (tercer caso) |M
Ejemplos de pares de fuerza, el volante de un coche, un destornillador, grifo, etc.
Al aplicar un par de fuerzas a un cuerpo se produce una rotación o una torsión. La magnitud
de la rotación (en definitiva el momento) depende del valor de las fuerzas que forman el par y
de la distancia entre ambas, llamada brazo del par, y del ángulo θ
Primera y segunda condiciones de equilibrio.
Resumimos a continuación las condiciones de equilibrio que hemos encontrado hasta ahora:
Una partícula está en equilibrio, (~a = 0) en un sist. de ref. inercial cuando la resultante de
todas la fuerzas que actúan sobre la partícula es cero. Para un sólido rígido: el centro de masas
del cuerpo tiene ~acdm = 0 si el vector suma de todas las fuerzas actuando sobre él es cero
P~
F = ~0
P
F =0
P x
F =0
P y
Fz = 0
Primera Condición del equilibrio, (la suma se extiende a todas las fuerzas externas que
actúan sobre el cuerpo o la partícula).
Hemos visto también que una 2ª condición para que una partícula o un sólido esté en equilibrio
es que no tenga tendencia a rotar. Un cuerpo rígido que en un sistema de referencia inercial no
49
está rotando alrededor de cierto punto no tiene momento angular alrededor de dicho punto y si
no inicia la rotación alrededor de ese punto no hay por tanto variación en el momento angular
⇒ la suma de los momentos de las fuerzas externas actuando sobre el cuerpo es cero. Es decir
un sólido rígido en equilibrio no puede tener ninguna tendencia a iniciar la rotación alrededor
de cualquier punto por lo que la suma de los momentos de las fuerzas externas respecto a
cualquier punto debe ser cero,
P ~
M = ~0 alrededor de qualquier punto
P
P Mx = 0
M =0
P y
Mz = 0
Segunda Condición del equilibrio. Cuando en un cuerpo se cumplen las dos condiciones
de equilibrio y está en reposo se dice que el cuerpo está en equilibrio estático. Un objero en
movimiento rectilíneo uniforme sin rotar estaría en equilibrio dinámico.
Centro de Gravedad
En la mayoría de problemas en situaciones de equilibrio una de las fuerzas actuando sobre los
cuerpos es el peso⇒ debemos saber calcular el momento producido por esta fuerza. El problema
es que esta fuerza actúa sobre todo el cuerpo y no sobre un sólo punto luego en principio no
sabríamos calcular el momento del peso. Podríamos hacerlo suponiendo que el peso del cuerpo
está concentrado sobre un punto llamado centro de gravedad.
50
~g decrece con la altura h, pero RT ≫ h ⇒ g ≈ cte (mayoría de los casos prácticos). Este hecho
implica que en la práctica el centro de gravedad coincida con el centro de masas del cuerpo.
Para demostrarlo calculamos el momento producido por el peso. El cuerpo es un sistema de
partículas de masa mi tal que la masa del cuerpo es
X
m=
mi
(10)
i
El peso actúa sobre todas estas partículas y apunta hacia el centro de la tierra ⇒ todos los
vectores peso w
~ i = mi~g tienen la misma dirección y sentido, son vectores paralelos. Si ~ri es el
vector de posición de cada partícula con respecto a un punto arbitrario O, el torque o momento
producido por cada una de estas fuerzas w
~ i respecto a ese punto es
~ i = ~ri ∧ w
M
~i
de donde el momento total debido a la gravedad es
~ =
M
X
i
~i =
M
X
~ri ∧ mi~g =
i
X
i
mi~ri
!
∧ ~g
de donde dividiendo y multiplicando por la masa total (10) del cuerpo se llega a
~ = ~rcdm ∧ m~g = ~rcdm ∧ w
M
~
P
pues ~rcdm = P1mi i mi~ri . Es decir, el momento total del peso de un cuerpo con respecto a un
punto O es el mismo que produciría el vector peso actuando en el centro de masas del cuerpo,
que llamamos tambiéncentro de gravedad del cuerpo. Es decir si la ~g es constante el centro de
gravedad coincide con el centro de masas del cuerpo.
51