capítulo ix. - Biblioteca Central
Anuncio

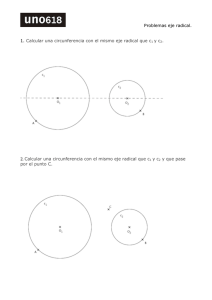
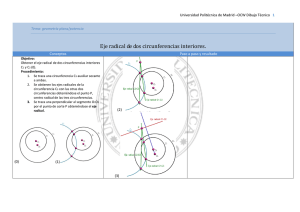
CAPÍTULO IX 119 POTENCIA E INVERSIÓN POTENCIA DE UN PUNTO RESPECTO A UNA CIRCUNFERENCIA Se llama así al producto de las distancias del punto a cada uno de los dos en que una secante que pasa por él corta a la circunferencia, tomando ese producto con signo + ó - según el punto sea exterior o interior a la circunferencia. PM = + MA x MB PN = - NC x ND Corolario: un Punto situado en la circunferencia tiene potencia nula. Potencia = MA . MB (minterior o exterior) TEOREMA IX-1 La potencia de un punto respecto a una circunferencia es independiente de la secante trazada, y vale: P = d2 - r 2 siendo d la distancia del punto al centro de la circunferencia, y r el radio de la misma. Dem.: Sea M un punto exterior. Trazamos la secante MAB y unimos M con el centro O. 120 Los triángulos MAD y MCB son semejantes, pues el ángulo en M es común, y los MDA y MB C son inscritos y abarcan el mismo arco; luego: MA MC = MD MB MA x MB = MD x MC = d2 - r 2 la cual es ya positiva. Si M fuese interior MAC y MDB son semejantes (d + r) (d - r) 121 MA MC = MD MB MA x MB = (r - d) (r + d) = r2 - d2 Pot = - MA x MB = d2 - r 2 Corolario: Para un punto exterior, la potencia es el cuadrado de la tangente desde este punto a la circunferencia: Mt 2 = d 2 - r2 por Pitágoras. TEOREMA IX - 2 Si dos pares de puntos AA' y BB' situados en 2 rectas secantes en P son concíclicos (es decir, por ellos pasa una circunferencia), se cumple, en valor y signo, que: PA X PA' = PBX PB' y recíprocamente. (Se considerará PAX PA' como positivo, si A y A' están en la misma semirrecta respecto a P). Dem.: Por potencia de P: PAX PA' = PB X PB' 122 Para demostrar el recí proco, trazamos la circunferencia que pasa por A, A' y B, la cual corta a PB en B" ( Fig. IX-6:), tal que, en virtud del teorema IX –1: PA X PA' = PB X PB'' ; y como PA X PA' = PB X PB' esto exige que PB" sea igual a PB', y en el mismo sentido. Por coincide con B', y los 4 puntos sean concíclicos. tanto B" Eje radical de 2 circunferencias Es el lugar geométrico de puntos del plano que tienen igual potencia respecto a las dos circunferencias. TEOREMA IX-3 El eje radical de dos circunferencias no concéntricas es una recta perpendicular a la línea de centros. 123 Dem.: Sean d 1, d2 las distancias de un punto P a los centros de dos circunferencias , y r1 y r 2 los radios de ellas. Para que las potencias de P sean iguales: d12 − r12 = d22 − r22 d12 − d 22 = r22 − r12 = Cte. Luego es necesario y suficiente que la diferencia de cuadrados de distancias a los dos centros sea constante. Se trata pues de una recta perpendicular a la línea de centros. NOTA: si las circunferencias son concéntricas, d1 = d2 ; y como los radios son distintos, no hay ningún punto que tenga igual potencia. Sin embargo, en atención a que los puntos muy lejanos v an teniendo potencias de razón más semejante, se suele decir que el eje radical en ese caso es "la recta del infinito" del plano. Corolarios: CONSTRUCCIÓN a) Si desde un punto del eje radical se pueden trazar tangentes a una de las circunferencias, se pueden trazar tamb ién tangentes, y de igual longitud, a la otra. b) Las tangentes comunes quedan dividi das en dos partes iguales por el eje radical. GEOMÉTRICA DEL EJE RADICAL Consideremos 4 casos: a) Las circunferencias son secantes: entonces el eje radical es la recta que une los puntos de intersección (que tienen potencia igual, nula, respecto a las dos). b) Las circunferencias son tangentes: entonces la tangente común es el eje radical. c) Las circunferencias son exteriores. En este caso, trazamos las tangentes comunes y unimos sus puntos medios, obteniendo así el eje radical. d) Las circunferencias son interiores. En este caso, buscaríamos un punto de igual potencia respecto a las dos, trazando dos tangentes de igual longitud t y buscando los puntos de la misma potencia, que están e n m1, y m2. El punto de intersección M, 124 pertenece al eje radical. Desde M trazamos la perpendicular a la línea de centros, que es el eje radical de las dos. Centro radical de tres circunferencias Se llama a s í al punto del plano (si existe), que tenga igual potencia respecto a 3 circunferencias dadas. Si los 3 centros no están alineados, entonces existen 3 ejes radicales: el de las circunferencias 1 y 2, el de las 1 y 3 y el de las 2 y 3. El de 1 y 2, y el de 2 y 3, se cortan en un punto que tiene igual potencia respecto a las 3 circunferencias; por tanto pertenece también al eje radical de 1 y 3. Es decir, los 3 ejes radicales concurren en el centro radical. Cuando dos circunferencias son concéntricas, uno de los 125 ejes radicales es la llamada "recta del infinito"; en ese caso no existe centro radical propiamente dicho; aunque p uede hallarse de un "centro radical en el infinito" en cierta dirección. Análogamente, cuando los 3 centros están alineados, los 3 ejes radicales son paralelos: no existe centro radical propio, pero puede decirse que está en el infinito, en la dirección señalada por los ejes radicales. INVERSIÓ N EN EL PLANO Sea el conjunto S' formado por todos los puntos del p lano a excepción del punto O. Inversión es una transformación de S' sobre sí mismo de tal forma que: a) 2 puntos homólogos (inversos) A y A' están alineados con O. b) OAxOA' = K K es una constante positiva o negativa, llamada potencia de inversión. a o se le llama centro de inversión. El producto OAxOA' se considerará positivo si A y o , y negativo en caso contrario. A' están en la misma semirrecta respecto a La potencia de inversión K, debe darse con indicación de la unidad usada. La inversión queda definida si se conocen O y K; o bien y se conocen O y un par de puntos inversos cualesquiera A y A', alineados con O. Corolario: La inversión es una transformación involutiva. TEOREMA IX-4 La circunferencia de centro O y radio K es doble. Dem.: Si K > O, A es inverso de sí mismo pues OA x OA' = K Si K < O , A' es el inverso de A y está también en la misma circunferencia. FIG: IX - 8 126 TEOREMA IX – 5 Dos pares de puntos inversos no alineados es tán en una circunferencia doble. Dem. :Sean A, A' y B y B' los pares de puntos inversos. OAX OA' = OB X OB' im plica que son concíclicos. Ahora bien, dado un punto C de la circunferencia que los contiene, su inverso C' también estará en la misma circunferencia por la misma razón. Corolario: cualquier circunferencia que contenga un par de puntos inversos es doble. TEOREMA IX-6 Si AA' y BB' son dos pares de puntos inversos no alineados, el ángulo OAB es igual al OB'A' (dicho de otro modo, las rectas AB y A'B' son antiparalelas respecto al ángulo AOB). OA x OA' OB x OB' OA OB = OB ' OA' lo que indica que los triángulos OAB y OB'A' son semejantes; luego OAB = OB'A' (Dos rectas tales que una de ellas forme con un lado de un ángulo el mismo ángulo que la otra con el otro lado, se llaman antiparalelas). 127 FIGURAS INVERSAS DE UNA RECTA TEOREMA IX -7 Una recta que pasa por el centro de inversión es doble. Dem.: el inve rso de cualquier punto de la recta está en la misma recta. NOTA: Debemos excluir de la inversión, por ahora, al centro O; por tanto, al decir "recta" en el teorema anterior, hay que entender una recta incompleta, de la que se excluye el punto O. TEOREMA IX-8 La figura inversa de una recta r que no pasa por O, es una circunferencia que pasa por O. El diámetro de esta circunferencia que pasa por O es perpendicular a r. Dem.: Desde O trazamos la perpendicular OA' a r. Hallamos A' inverso de A. Cualquier punto B de la recta tiene un inverso B' tal que: OAˆ B = OBˆ ' A' = 90º Lo que indica que B' está sobre la circunferencia de diámetro OA'. 128 FIGURA INVERSA DE UNA CIRCUNFERENCIA TEOREMA IX – 9 La figura inversa de una circunferencia que pasa por O, es una recta perpendicular al diámetro que pasa por O. (Teorema recíproco del anterior). Dejamos la demostración para el lector. NOTA: En los dos teoremas anteriores, se sobreentiende que a la circunferencia se le excluye el punto O. TEOREMA IX-10 La figura inversa de una circunf erencia c que no pasa por el centro de inversión O, es otra circunf erencia c ’ homotecia de c , con centro de homotecia O y razón de homotecia K/p, siendo K la potencia de inversión y p la potencia de O respecto a c. Dem.: Sea A y B dos puntos de c y A' y B' sus inversos. OAX OA' = OB X OB ' = K ; dividiendo por OAX OB : OA' OB ' K K = = = OB OA OAXOB P Lo que indica que A' es homotético de B (y B’ es homotético de A) con centro O y razón k p . 129 CONSERVACIÓN DE ÁNGULOS EN LA INVERSIÓ N TEOREMA IX - 11 La inversión conserva los ángulos que forman 2 curvas y cambia su sentido. Dem.: Primero demostraremos que siendo BB' y CC' 2 pares de puntos homólogos alineados con O; y AA' otro par de puntos fuera de la recta anterior, Xˆ = OAˆ C = OAˆ B Yˆ + OBˆ ' A' = ACˆ ' A' BAˆ C = − B' Aˆ ' C' OCˆ ' A'−OBˆ ' A' = OAˆ C − OAˆ B ˆ C ) tiene sentido positivo, luego los dos ángulos son iguales; pero uno de ellos ( BA ˆ ' C ' ) negativo. y el otro ( B' A y= Si suponemos 2 curvas que se cortan, m y n; y sus inversas m' y n' 130 los ángulos BAˆ C y B' Aˆ ' C ' son iguales; si OB tiende a confundirse con OA, en el límite AB y AC se convierten en las tangentes a m y n en A; y lo mismo A'B' y A'C' pasan a ser tangentes de m' y n' . El ángulo que forman las tangentes es el mismo que forman las curvas. Luego las curvas forman ángulos iguales y con sentidos opuestos. DISTANCIA ENTRE PUNTOS INVERSOS TEOREMA IX-12 Si A' y B' son inversos de A y B respecto a O, con potencia K: K A' B'. = AB x OAxOB Demostración Como ya hemos visto antes, los triángulos OAB y OB'A' son semejantes: OA OB AB = = OB ' OA' B' A' A' B' = ABx OB ' OA y multiplicando por OB numerador y denominador: A' B ' = ABx K OB ' xOB = ABx OAxOB OAxOB 131 GENERALIZACIÓN DE LA INVERSIÓ N El único punto del plano que no podemos hacer entrar, hasta ahora, ni como objeto ni como imagen, en la transformación inversiva, es el centro de inversión O. Cuando un punto A se mueve acercándose a O, su inverso A' se aleja. Si A tiende a O, A' se aleja más allá de todo límite. En vista de ello, se puede ampliar la inversión a todo el plano, si se considera que el inverso de O es un "punto en el infinito", en cualquier dirección. APLICACIONES DE LA POTENCIA Y LA INVERSIÓN Vamos a ver algunas de las muchísimas aplicaciones de la potencia e inversión para la solución de problemas geométricos: Ejemplo 1 Trazar una circunferencia que pase por 2 puntos tangente a una recta A y B y sea r Uniendo A con B, AB corta a r en M. Desde este punto al de tangencia T va una distancia MT tal que: MT2 = MB x MA lo que permite obtener T y trazar la circunferencia. El lector puede ver como obtener MT usando la tangente de M a cualquier circunferencia que pase por A y B. 132 Ejemplo 2 Obtener segmentos inversamente proporcionales a otros varios. Hasta el presente, sabemos cómo obtener segmentos direc tamente proporcionales a a, b, y c. Se colocan a, b y c sobre la recta y sobre los segmentos determinados sobre son directamente proporcionales a a b c = = a' b' c' a, b y r r ' por un sistema de paralelas c: en virtud del teorema de Thales Pretendemos ahora obtener un juego inversamente proporcionales a a, b y a' b' y c' de segmentos c: a x a' = b b' = c c ' Desde un punto P cortamos a una circunferencia (con un compás) a una distancia a (Punto A). Encontramos A', intersección de PA circunferencia. PA' = a'; de la misma forma hallamos b ' y c '. con la 133 Así obtenemos a ', b ' y c ' NOTA: cualquier otro juego a '', b '' y c '' de segmentos inversamente proporcionales a a, b y c que pudiéramos obtener, se rían directamente proporcionales respecto a a', b' y c': a a' = b b' = c c' a a" = b b" = c c" a' b' c ' = = a' ' b' ' c ' ' Puede aplicarse el procedimiento, por ejemplo, para resolver un triángulo conociendo las 3 alturas (que son inversamente proporcionales a los lados, como puede verse por la fórmula del área: S= 1 1 1 aha = bhb = chc 2 2 2 Ejemplo 3 Trazar una circunferencia x que pase por un punto P y sea tangente a dos circunferencias dadas m y n. Una inversión de centro P transforma x en una recta x'; m y n en otras 2 circunferencias m' y n', a las cuales será tangente la recta x'. Trazamos pues x', recta tangente común a m' y n' (hasta 4 soluciones; ó 2; ó ninguna); y buscamos ya x, inversa de x'. Véase como la resolución de este ejercicio sigue el esquema citado antes, de transformar, resolver e invertir la transformación. 134 Si como potencia de inversión se toma la potenc ia de P respecto a m, esta circunferencia se invierte en ella misma, simplificándose el dibujo. A partir de este ejercicio, se puede resolver el problema de trazar circunferencias tangentes a otras tres. Ejemplo 4 Deducción del teorema de Ptolo meo: "En todo cuadrilátero, la suma de los productos de los lados opuestos es igual o mayor que el producto de las diagonales, según sea o no inscriptible". Sea ABCD un cuadrilátero inscriptible. Tomando A como centro de inversión, B' C' y D' caen sobre una recta r: B' D' = B ' C' + C' D' En virtud del teorema IX-12 BDx K ABxAD = BCx K ABxAC + CDx K ACxAD multiplicando por AB x AC x AD y dividiendo por /K/: BD x AC = BC y AD + CD x AB quedando demostrado para cuando sea inscriptible. Si no lo es, entonces B', C' y D' no estarían en una recta, o sea 135 B' D' < correspondiente. B' C' + C' D' obteniéndose la demostración APARATO INVERSOR MECÁ NICO DE PEAUCELLIER De igual forma que el pantógrafo realiza mecánicamente la transformación de figuras por homotecia, el inversor de Peaucellier realiza la inversión. Las barras AB, BC, CD y DA tienen igual longitud; tam bién son iguales entre sí las barras OA y OC. El punto O está fijo al plano del dibu jo, permitiendo el giro sin des lizamiento. A, B, C y D tienen articulaciones. O B y D están alineados por estar en la mediatriz de AC. Podemos suponer trazada una circunferencia con centro en A que pase por B y D, y en ella: PB x PD = d2 - r 2 = OA 2 - AB2 = Por tanto, B y D son Puntos inversos. Cte. Si en B hay una punta y en D un lápiz, éste trazará la curva inversa de la figura que recorra B. EJERCICIOS CAPÍTULO IX 136 Ejercicios resueltos IX-1. Dada una circunferencia c y 2 puntos exteriores a ella A y B, trazar una circunferenc ia que pase por A y B y sea tangente a c . Resolución: Suponiendo el problema resuelto: Si unimos A con B y trazamos la tangente común, las 2 rec tas se cortan en P, punto de igual potencia respecto a las dos circunferencias x y c. El punto P tendría la misma potencia PA x PB respecto a c ualquier circunferencia auxiliar y que pasara por A y B: lo que indica que P es el centro radical de x, y y c. 137 El precedente análisis indica la forma como se puede obtener la solución: − trazar una circunferencia auxiliar -y- que pase por A y B. − obtener el eje radical de c y de -y- . − la intersección de dicho eje radical con AB da el punto P, cuya tangente PT (2 soluciones máximo) da el punto de tangencia T entre x y c. − la circunferencia que pasa por A, B y T es x. Esta circunferencia puede hallarse cómodamente trazando la mediatriz de AB y uniendo T con C: donde se corten, allí está el centro X. Aplicación: Datos: Trazamos -y-, obtenemos M, N y P; luego T, luego x: 138 IX-2. Construir un triángulo conociendo las 3 alturas. Resolución: Co mo las alturas son inversamente proporcionales a los lados (ver ejemplo 2, cap. IX), pode mos obtener los lados a', b' y c' de un triángulo semejante al que buscamos si: a'ha = b'hb = c'hc a' podemos tomarlo arbitrariamente, y b' y c' los calcularemos gráficamente usando la potencia de un punto respecto a una circunferencia (ver ejemplo 2, cap. IX) o bien por inversión como haremos más adelante. Construido el triángulo semejante al buscado, lo ampliaremos o reduciremos hasta que sus alturas coincidan con los datos. Aplicación: Datos: 139 Tomamos arbitrariamente: a’ Calculamos b' mediante la propiedad de que las rectas que unen 2 puntos y sus inversos son antiparalelas respecto a las que unen los mismos puntos con el centro de inversión (ver Teorema IX-6); OHA = ha; OA" = a'; OHB = hb; etc. Construimos el triángulo A'B'C': 140 y lo ampliamos trazando una paralela a C'B' de forma que la altura sea ha: Como comprobación de la precisión de los dibujos, vemos que las alturas del triángulo ABC, hb y hc , coinciden sensible mente con los datos. IX-3. Hallar gráficamente 2 segmentos x e y tales que: x - y = AB xy = (CD) 2 siendo AB y CD segmentos dados. Resolución: Aplicando las propiedades de la potencia de un punto C respecto a una circunferencia: 141 observamos que los segmentos x e y cumplen las condiciones pedidas. Se trata pues de construir una circunferencia cualquiera que pase por A y B, y en la recta AB determinar un punto cuya tangente a la circunferencia tenga longitud CD (desde P has ta el punto de tangencia). Trazamos pues cualquier circunferencia que pase por A y B, por ejemplo, la de diámetro AB. Levantamos una tangente en B, por ejemplo, BQ = CD. El punto Q tiene una tangente i gual a la buscada. Una rotación alrededor de O mueve Q en una circunferencia, cuyos puntos tienen tangent es de igual longitud. Así encontramos P, sobre la recta AB y cuya tangente es igual a CD. Los segmentos buscados son PA y PB. IX-4. Conociendo el centro de inversión O y 2 puntos homólogos A y A', hallar la figura inversa de una circunferencia m que no pasa por O. Resolución: m' será una circunferencia homotética de m con centro en O (Teorema IX-10); por tanto su centro M' está en la recta MO; y trazando desde O una tangente a m, es también tangente a m': 142 Podemos trazar la tangente OT, la recta OM; y obtener T' me diante la propiedad del antiparalelismo de segmentos que unen puntos inversos (Teorema IX-6) ubicamos T'; y en la perpendicular T'M' a OT está el centro M' Aplicación:. 143 Nota: este problem a puede resolverse de formas muy variadas, por ejemplo, tomando 3 puntos en la circunferencia m y buscando los 3 inversos. IX-5. Hallar la figura inversa de un cuadrado, siendo el centro de inversión el mismo centro del cuadrado. Resolución: Cada lado del cuadrado dará lugar a un arco de circunferencia (que pasa por el centro de inversión), de ángulo central 180º : Los cuatro lados del cuadrado dan: 144 Hemos escogido arbitrariamente la potencia de inversión, que no entraba como dato en el enunciado del problema. Una variación de la misma agrandaría o reduciría la figura inversa, que siempre sería homotética a la obtenida respecto a O. Ejercicios propuestos IX-6. Hallar la figura inversa de un cuadrado, siendo un vértice el centro de inversión. IX-7. Hallar la figura inversa de un triángulo, siendo un v értice el centro de inversión. ¿Cuáles serían los inversos de los puntos del interior del triángulo? IX-8. Hallar el lugar geométrico de puntos del plano que pueden ser centros de inversión para que dos circunferencias dadas sean dobles. (R.: el eje radical de las dos, si existe.) IX-9. Idem para que 3 cir cunferencias dadas sean dobles. (R.: el centro radical, si existe,) IX-10. Dadas 3 circunferencias que tienen un punto común, trazar circunferencias tangentes a las tres. (Sugerencia: use el punto común como centro de una inversión.)