4ta Parte

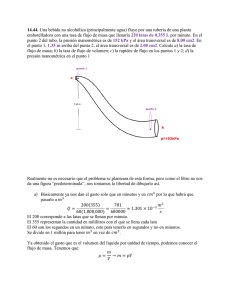
UNIVERSIDAD TECNOLÓGICA NACIONAL
Facultad Regional Rosario
UDB Física
Cátedra FÍSICA I
4ta PARTE
PRÁCTICA Nº 10: MOVIMIENTO ARMONICO SIMPLE
10-1. Una pieza de una máquina está en MAS con frecuencia de 5 Hz y amplitud de 1,80 cm. ¿Cuánto
tarda la pieza en ir de x = 0 a x = -1,80 cm?
10-2. Un cuerpo de masa desconocida se une a un resorte ideal con constante de fuerza de 120 N/m. Se
observa que vibra con una frecuencia de 6 Hz. Calcular:
a) El periodo.
b) La frecuencia angular.
c) La masa del cuerpo.
10-3. Una cuerda de guitarra vibra con una frecuencia de 440 Hz. Un punto en su centro se mueve en
MAS con amplitud de 3 mm y ángulo de fase cero,
a) Escriba una ecuación para la posición del centro de la cuerda en función del tiempo,
b) ¿Qué magnitud máxima tienen: la velocidad y la aceleración del centro de la cuerda?
10-4. Un bloque de 2 kg, que se desliza sin fricción, se conecta a un resorte ideal con k = 300 N/m. En t =
0, el resorte no está estirado ni comprimido y el bloque se mueve en la dirección negativa a 12 m/s.
a) Calcular la amplitud y el ángulo de fase,
b) Escribir una ecuación para la posición en función del tiempo.
10-5. Una silla de 42,5 kg se sujeta a un resorte y se le permite oscilar. Cuando la silla está vacía, tarda
1,3 segundos en efectuar una vibración completa. Cuando una persona se sienta en ella, sin tocar el piso
con los pies, la silla tarda 2,54 s en efectuar un ciclo. Calcular la masa de la persona.
10-6. Un objeto está en movimiento armónico simple con periodo de 0,3 s y amplitud de 6 cm. En t = 0,
el objeto está instantáneamente en reposo en x = 6 cm. Calcule el tiempo que el objeto tarda en ir de x =
6 cm a x = - 1,50 cm.
10-7. El chasis de un automóvil de 1200 kg de masa está soportado por cuatro resortes de constante
elástica 20000 N/m cada uno. Si en el coche viajan cuatro personas de 60 kg cada una, hallar la
frecuencia de vibración del automóvil al pasar por un bache.
10-8. Un resorte de acero tiene una longitud de 15 cm y una masa de 50 gramos. Cuando se le cuelga en
uno de sus extremos una masa de 50 gramos se alarga, quedando en reposo con una longitud de 17 cm.
Calcular:
a) La constante elástica del resorte.
b) La frecuencia de las vibraciones si se le cuelga una masa de 90 gramos y se le desplaza
ligeramente de la posición de equilibrio.
10-9. Una masa de 200 gramos unida a un muelle de constante elástica K = 20 N/m oscila con una
amplitud de 5 cm sobre una superficie horizontal sin rozamiento.
a) Calcular la energía total del sistema y la velocidad máxima de la masa.
b) Hallar la velocidad de la masa cuando la elongación sea de 3 cm.
c) Hallar la energía cinética y potencial elástica del sistema cuando el desplazamiento sea igual a 3
cm
d) ¿Para qué valores de la elongación la velocidad del sistema es igual a 0,2 m/s?
50
50
Ing. Ricardo Pérez Sottile
FÍSICA I
Ing. Ricardo Pérez Sottile
FÍSICA I
10-10. ¿En qué posiciones y en qué instantes se hacen iguales las energías cinética y potencial elástica de
un cuerpo que describe un mas?
10-11. Cuando la elongación de un móvil que describe un mas es la mitad de la amplitud, ¿qué
porcentaje de su energía total corresponde a la energía cinética y qué porcentaje a la potencial elástica?
10-12. Un objeto se mueve en MAS. Cuando está desplazado 0,6 m a la derecha de su posición de
equilibrio, tiene una velocidad de 2,2 m/s a la derecha y una aceleración de 8,4 m/s2 a la izquierda. ¿A
qué distancia de este punto se desplazará el objeto antes de detenerse momentáneamente para iniciar
su movimiento a la izquierda?
10-13. La punta de una aguja de una máquina de coser se mueve con MAS sobre el eje x con una
frecuencia de 2,5 Hz. En t = 0, sus componentes de posición y velocidad son +1,1 cm y -15 cm/s. Calcular
la componente de la aceleración de la aguja en t = 0
10-14. El extremo superior de un resorte ligero de longitud natural 20 cm se mantiene fijo, colgándose
del otro extremo masas de 40 g y 80 g, esta última por debajo de la primera. La longitud del resorte es
ahora 26 cm. Si se suprime la segunda masa.
a) Calcular la frecuencia del movimiento armónico simple con que se mueve la masa de 40 g
b) Calcular la máxima energía cinética de esta masa.
10-15. En la Tierra, cierto péndulo simple tiene un periodo de 1,6 s. ¿Qué periodo tendrá en Marte,
donde g = 3,71m/s2?
10-16. Un péndulo simple de 80 cm de longitud oscila con amplitud de 10 cm. Calcular su velocidad en el
punto más bajo.
10-17. En la Figura 10-1, la bola superior se suelta del reposo, choca con la bola estacionaria y se pega a
ella. Ambos hilos tienen 50 cm de longitud. La bola superior tiene masa de 2 kg y está inicialmente 10
cm más alta que la inferior, cuya masa es de 3 kg. Calcule la frecuencia y el desplazamiento angular
máximo del movimiento después del choque.
0,1 m
Figura 10-1
10-18. Cierto reloj despertador hace tic cuatro veces cada segundo, y cada tic representa medio
periodo. La rueda de balance consiste en un aro delgado de 0,55 cm de radio conectada al vástago de
balance por rayos de masa despreciable. La masa total de la rueda es de 0,90 g. ¿Qué constante de
torsión tiene la espiral?
10-19. Queremos colgar un aro delgado de un clavo horizontal y hacer que tenga una oscilación
completa con ángulo pequeño una vez cada 2 segundos ¿Qué radio debe tener el aro?
Obs.: Momento de Inercia del aro con respecto al centro de masa: M . R2
4° Parte: Prácticas N° 10, 11 y 12
51
FÍSICA I
10-20. Una biela de 1,80 kg de un motor de coche pivota alrededor de un filo de navaja horizontal como
se muestra en la Figura 10-2. El centro de masa de la biela se encontró por balanceo y está a 0,2 m del
pivote. Cuando la biela se pone a oscilar con amplitud corta, completa 100 oscilaciones en 120 s.
Calcular el momento de inercia de la biela respecto al eje de rotación en el pivote.
0,2 m
c.m.
Figura 10-2
10-21. Dos esferas de igual masa y 3 cm de diámetro penden de un único alambre. El centro de una
esfera se encuentra a 1 m por debajo del punto de suspensión y el centro de la otra a 50 cm por debajo
del centro de la primera esfera. Calcular el periodo de oscilación.
Obs.: Inercia de las esferas con respecto a su centro de masa: 2. M . R2/5
10-22. Dos varillas delgadas idénticas (Figura 10-3), cada una con masa m y longitud L, se unen en
ángulo recto para formar un objeto en forma de L, el cual se balancea sobre un filo. Si el objeto se desvía
un poco, oscila. Calcular la frecuencia de oscilación.
Obs.: Momento de Inercia de una varilla delgada con respecto a un extremo: 1/3 .M . L2
Figura 10-3
10-23. Una llave inglesa de 0,5 kg de masa se suspende de uno de sus extremos y se la hace oscilar como
un péndulo físico. El período es 0,9 segundos y el punto de suspensión dista 15 cm del centro de masa.
a) ¿Cuál es el momento de inercia respecto de un eje que pase por el pivote?
b) Si la llave se desplaza inicialmente 0,1 radianes de su posición de equilibrio ¿Cuál será su
velocidad angular al pasar por dicha posición?
4° Parte: Prácticas N° 10, 11 y 12
52
FÍSICA I
UDB Física
Cátedra FÍSICA I
UNIVERSIDAD TECNOLÓGICA NACIONAL
Facultad Regional Rosario
PRÁCTICA Nº 11: HIDROSTATICA
11-1. ¿A qué profundidad del mar hay una presión manométrica 1 . 105 Pa? Suponer que la densidad del
agua de mar igual a 1030 kg/m3
11-2. Un barril contiene una capa de aceite (densidad de 600 kg/m3) de 0,12 m sobre 0,25 m de agua
(densidad 1000 kg/m3).
a) ¿Qué presión manométrica hay en la interfaz aceite-agua?
b) ¿Qué presión manométrica hay en el fondo del barril?
11-3. El liquido del manómetro de tubo abierto de la Figura 11-1 es mercurio, y1 = 3 cm y y2 = 7 cm. La
presión atmosférica es de 980 milibares.
a) ¿Qué presión absoluta hay en la base del tubo en U?
b) ¿Y en el tubo abierto 4 cm abajo de la superficie libre?
c) ¿Qué presión absoluta tiene el aire del tanque?
d) ¿Qué presión manométrica tiene el gas en Pascales?
Obs.: Densidad del Mercurio: 13600 kg/m3
11-4. Las dimensiones de una piscina rectangular son 25 m de largo, 12 m de ancho y 2 m de
profundidad. La densidad del agua es de 1000 kg/m3. Calcular:
a) La presión manométrica en el fondo de la piscina.
b) La fuerza total en el fondo debida al agua que contiene.
c) La fuerza total sobre una de las paredes de 12 m por 2 m.
d) La presión absoluta en el fondo de la piscina en condiciones atmosféricas normales, al nivel del
mar.
11-5. Un cilindro alto con área transversal de 12 cm2 se llenó parcialmente con mercurio hasta una
altura de 5 cm. Se vierte lentamente agua sobre el mercurio (los dos líquidos no se mezclan). ¿Qué
volumen de agua deberá añadirse para aumentar al doble la presión manométrica en la base del
cilindro?
11-6. Un corto deja sin electricidad a un submarino que está 30 m bajo la superficie del mar (densidad =
1030 kg/m3). Para escapar, la tripulación debe empujar hacia afuera una escotilla en el fondo que tiene
un área de 0,75 m2 y pesa 300 N. Si la presión interior es de 1 atm, ¿Qué fuerza hacia abajo se debe
ejercer sobre la escotilla para abrirla?
po = pa
h
Líquido
desconocido
2 cm
y2
14 cm
Presión p
y1
Mercurio
Figura 11-2
Figura 11-1
4° Parte: Prácticas N° 10, 11 y 12
53
FÍSICA I
11-7. En el tubo en U de la Figura 11-2, se ha llenado la rama
de la derecha con mercurio y la de la izquierda con un líquido
de densidad desconocida. Los niveles definitivos son los
indicados en el esquema. La densidad del mercurio es 13,6
g/cm3. Hallar la densidad del líquido desconocido.
F1
A1
11-8. El pistón de un elevador hidráulico para autos tiene 0,3
m de diámetro. ¿Qué presión manométrica, en Pascales y en
atm, se requiere para levantar un auto de 1200 kg?
11-9. Un recipiente cerrado que contiene líquido
(incompresible) está conectado al exterior mediante dos
pistones, uno pequeño de área A1 = 0,15 m2 y uno grande de
área A2 = 3 m2 como se ve en la Figura 11-3. Ambos pistones
se encuentran a la misma altura. Si se aplica una fuerza F1 =
500 N hacia abajo sobre el pistón pequeño. ¿Puede elevar un
auto cuya masa es de 940 kg?
A2
Figura 11-3
F2
11-10. ¿Cuál es densidad de un cuerpo si flota en el agua de modo que emerge el 35 % de su volumen?
Densidad del agua 1000 kg/m3
11-11. Un bloque cúbico de madera de 10 cm por lado flota en la interfaz entre aceite y agua con su
superficie inferior 1,5 cm bajo la interfaz (Figura 11-4). La densidad del aceite es de 790 kg/m3.
a) ¿Qué presión manométrica hay en la superficie de arriba del bloque?
b) ¿Y en la cara inferior?
c) ¿Qué masa tiene el bloque?
11-12. Un recipiente contiene una capa de agua (ρAGUA = 1000 kg/m3), sobre la que flota una capa de
aceite, de densidad ρACEITE = 800 kg/m3. Un objeto cilíndrico de densidad desconocida ρ cuya área en la
base es A y cuya altura es h, se deja caer al recipiente, quedando a flote finalmente cortando la
superficie de separación entre el aceite y el agua, sumergido en esta última hasta la profundidad de
2.h/3 como se indica en la Figura 11-5. Determinar la densidad del objeto.
ACEITE
8,5 cm
MADERA
Madera
Madera
10 cm
1,5
10 cm
ACEITE
h
2.h
3
AGUA
AGUA
Figura 11-5
Figura 11-4
4° Parte: Prácticas N° 10, 11 y 12
54
FÍSICA I
11-13. Una plancha de hielo flota en un lago de agua dulce. ¿Qué volumen mínimo debe tener para que
una mujer de 45 kg pueda pararse en ella sin mojarse los pies?
Obs.: Densidad del hielo: 920 kg/m3
Densidad del agua: 1000 kg/m3
11-14. Una esfera de plomo llena de aire, con radio R = 0,1 m, se encuentra totalmente sumergida en un
tanque de agua como se ve en la figura. ¿ Cuál es el espesor de la capa de plomo, si la esfera ni flota ni
se hunde? La densidad del plomo es ρPb = 11300 Kg/m3
Obs.: VESFERA = 4/3 . π . R3
11-15. El bloque de área 1 m2 y espesor 10 cm de la Figura 11-6-a se coloca sobre agua de densidad
igual a 1000 kg/m3, quedando la mitad sumergido.
a) Calcular la densidad de la tabla.
b) Calcular el peso de otro bloque que habría que colocar sobre el otro bloque para que quede
sumergido 8 cm (Figura 11-6-b)
Madera
10 cm
Madera
5 cm
10 cm
(a)
8 cm
(b)
Figura 11-6
11-16. Una boya cilíndrica de 10 cm de radio flota sumergida hasta la mitad en el agua cuya densidad es
de 1000 kg/m3. Trepa sobre ella una rana de 0,25 kg ¿En cuanto se incrementa su altura sumergida?
11-17. Una esfera maciza de 10 cm de radio y densidad 1,4 g/cm3 flota en mercurio hasta el ecuador
sostenida por una cuerda del fondo del recipiente.
a) Calcular la tensión de la cuerda
b) Si se corta la cuerda calcular que porcentaje de la esfera queda sumergido.
Obs.: Densidad del Mercurio: 13600 kg/m3
Volumen de la esfera = 4/3 . π . R3
11-18. Un globo tiene una masa igual a 5 gramos e inflado un radio de 20 cm ¿Cuántos globos inflados
con helio se necesitan para elevar del suelo a un chico de 20 kg de masa?
Obs.: ρHELIO = 0,18 kg/m3
ρAIRE = 1,29 kg/m3
Volumen del globo inflado= VOLESFERA = 4/3 . π .R3
4° Parte: Prácticas N° 10, 11 y 12
55
FÍSICA I
UDB Física
Cátedra FÍSICA I
UNIVERSIDAD TECNOLÓGICA NACIONAL
Facultad Regional Rosario
PRÁCTICA Nº 12: HIDRODINÁMICA
12-1. Una regadera tiene 20 agujeros circulares cuyo radio es de 1 mm. La regadera está conectada a un
tubo de 0,80 cm de radio. Si la velocidad del agua en el tubo es de 3 m/s ¿Con qué velocidad saldrá el
agua por los agujeros? Densidad del agua 1000 kg/m3.
12-2. Un tanque sellado que contiene agua de mar hasta una altura de 11 m contiene también aire
sobre el agua a una presión manométrica de 3 atm. Sale agua del tanque a través de un agujero
pequeño en el fondo. Calcular la rapidez de salida del agua.
12-3. Se corta un agujero circular de 6 mm de diámetro en el costado de un tanque de agua grande, 14
m debajo del nivel del agua en el tanque. El tanque está abierto al aire por arriba. Calcular:
a) La rapidez de salida.
b) El volumen descargado por unidad de tiempo.
12-4. ¿Qué presión manométrica se requiere en una toma municipal de agua para que el chorro de una
manguera de bomberos conectada a ella alcance una altura vertical de 15 m? (Suponga que la toma
tiene un diámetro mucho mayor que la manguera)
12-5.En un punto de una tubería, la rapidez del agua es de 3 m/s y la presión manométrica es de 5 . 104
Pa. Calcular la presión manométrica en otro punto de la tubería, 11 m más abajo, si el diámetro del tubo
ahí es el doble que en el primer punto.
12-6. Se descarga agua de un tubo horizontal cilíndrico a razón de 465 cm3/s. En un punto del tubo
donde el diámetro es de 4,1 cm, la presión absoluta es de 1,6 . 105 Pa. ¿Qué diámetro tiene una
constricción del tubo donde la presión se reduce a 1,20 x 105 Pa?
12-7. Un recipiente cilíndrico, abierto por arriba, tiene 25 cm de altura y 10 cm de diámetro. Se hace un
agujero circular de área 1,5 cm2 en el fondo del recipiente. Se está vertiendo agua en el recipiente
mediante un tubo que está arriba, a razón de 2,4 . 10-4 m3/s. ¿A qué altura subirá el agua en el
recipiente?
12-8. Fluye agua continuamente de un tanque abierto como en la Figura 12-1. La altura del punto 1 es
de 10 m, y la de los puntos 2 y 3 es de 2 m. El área transversal en el punto 2 es de 0,0489 m2 y en el
punto 3 es de 0,016 m2. El área del tanque es muy grande en comparación con el área transversal del
tubo. Calcular :
a) El caudal de salida en m3/s.
b) La presión manométrica en el punto 2.
1
10 m
2
3
2m
Figura 12-1
4° Parte: Prácticas N° 10, 11 y 12
56
FÍSICA I
12-9. El tubo horizontal de la Figura 12-2 tiene un área transversal A1 = 40 cm2 en la parte más ancha y
A2 = 10 cm2 en la constricción. Fluye agua en el tubo, cuya descarga es de 6 . 10-3 m3/s. Calcular:
a) La rapidez de flujo en las porciones ancha y angosta.
b) La diferencia de presión entre estas porciones.
c) La diferencia de altura entre las columnas de mercurio en el tubo con forma de U.
12-10. En la Figura 12-2 las secciones de la tubería son A1 = 40 cm2 y A2 = 12 cm2, la velocidad del agua
en la sección 1 es de 0,1 m/s. Calcular el desnivel entre ambas ramas del manómetro, si el líquido que
contiene es mercurio (ρHG = 13600 kg/m3).
1
2
h
h
v1
v2
1
2
Figura 12-3
Figura 12-2
12-11. Consideremos un tubo de Venturi como el de la Figura12- 4 con tres tomas de presión estática
verticales. El diámetro de la sección 1 es de 50 cm y de 20 cm en la sección 2 del estrechamiento.
Cuando circula un caudal de agua de 200 litros/s, el nivel del agua en los tubos de la izquierda y derecha
se encuentra a 3 metros por encima del eje de la tubería.
a) ¿Cual es la presión manométrica en los puntos 1 y 2?
b) ¿Hasta que altura subirá el agua por el tubo central?
c) ¿Para que caudal de agua se succionará aire por el tubo central?
h1
h2
1
2
3
Figura 12-4
12-12. Un sifón como el mostrado en la Figura12-5 adjunta puede ser utilizado para extraer líquido de
un depósito. Una vez todo el tubo del sifón AC está completamente lleno de líquido, éste será
succionado del depósito mientras la superficie libre esté por encima del extremo del sifón abierto al
aire C. Suponiendo que el sifón succiona agua del depósito.
a) Calcular la velocidad de salida del líquido por el extremo C.
b) Calcular la presión absoluta en el punto B.
c) ¿A que altura máxima sobre el punto C puede estar el punto B para que el sifón siga
funcionando correctamente?
4° Parte: Prácticas N° 10, 11 y 12
57
FÍSICA I
12-13. De un gran depósito de agua, cuyo nivel se mantiene constante fluye agua que circula por los
conductos de la Figura 12-6 hasta salir por la abertura D, que está abierta al aire. La diferencia de
presión entre los puntos A y B es PB - PA = 500 Pa. Sabiendo que las secciones de los diferentes tramos de
la cañería son AA= AC = 10 cm2 y AB=20 cm2.
a) Calcular las velocidades del agua en los puntos A, B, C, de la cañería.
b) Calcular las presiones en los puntos A, B, C, de la cañería.
B
A
A
Madera
h
Figura 12-5
B
C
D
Figura 12-6
C
12-14. El depósito abierto de la Figura12- 7, de grandes dimensiones y paredes verticales, contiene agua
hasta una altura H = 5m. Se practica un orificio en la pared del depósito, a una profundidad h = 1 m por
debajo de la superficie libre del agua. El
1
chorro de agua sale horizontalmente y, tras
h
describir una trayectoria parabólica, llega al
2
suelo a una distancia "x" del pie del
depósito.
a) ¿Cuál es el alcance "x" del chorro
H
sobre el plano horizontal?
b) ¿Será posible abrir un segundo
orificio, a distinta profundidad, de
modo que el chorro que salga de él
tenga el mismo alcance que antes? En
x
caso afirmativo, ¿A qué profundidad?
Figura 12-7
4° Parte: Prácticas N° 10, 11 y 12
58
FÍSICA I
RESPUESTAS
10-1. 0,05 s
10-2. a) 0,167 s b) 37,7 rad/s c) 0,084 kg
10-3. a) x = 3 .10-4 m . cos 2 . π . 440 ciclos/s . t b) 8,3 m/s y 2,29 . 104 m/s2
10-4. a) 0,98 m θ = 90° = π/2 b) - 0,98 m . sen (12,25 rad/s . t )
10-5. 119,74 kg
10-6. 0,087 s
10-7. 1,19 Hz
10-8. a) 24,5 N/m b) f= 2,1 Hz
10-9. a) 0,025 J y 0,5 m/s b) ± 0,4 m/s c) Ec = 0,016 J y Epe = 0,009 J d) ± 4,58 cm.
10-10. A / 2
10-11. La energía cinética representa el 75% de la total y la elástica el 25%.
10-12. 0,84 m
10-13. - 2,714 m/s2
10-14. a) 3,523 ciclos/s b) 0,474 J
10-15. 2,6 s
10-16. 0.35 m/s
10-17. 14° 32´2¨ y 0,705 Hz
10-18. 4,29 10-6 N m/rad
10-19. 0,496 m
10-20. 0,129 kg . m2
10-21. 2,288 s
10-22.
l
3.g
4.π
2 L
10-23. a) 0,0186 kg . m2 b) 0,7 rad/s
11-1. 9,91 m
11-2. a) 705,6 Pa b) 3155,6 Pa
11-3. a) 1,073 .105 Pa b) 1,033 .105 Pa
c) 1,033 .105 Pa d) 5331,2 Pa
11-4. a) 19600 Pa b) 5,88 .106 N
c) 235299 N d) 120925 Pa
11-5. 0,816 litros
11-6. 227415 N
11-7. 1943 kg/m3
11-8. 166390 Pa = 1,64 atm
11-9. Si, puede levantar 9212 N
11-10. 650 kg/m3
11-11. a) 116,13 Pa b) 921,2 Pa c) 0,8215 kg
11-12. 933,33 kg/m3
11-13. 0,5625 m3
11-14. 0,304 cm
11-15. a) 500 kg/m3 b) 294 N
11-16. 0,8 cm
11-17. a) 221,67 N b) 10,3 %
11-18. 621 globos
12-1. 9,6 m/s
12-2. 15,9 m/s
4° Parte: Prácticas N° 10, 11 y 12
59
FÍSICA I
12-3. a) 16,56 m/s b) 0,468 litros/s
12-4. 1,47 . 105 Pa
12-5. 1,62 . 105 Pa
12-6. 0,833 cm
12-7. 0,13 m
12-8. a) 0,20 m3/s b) 70007 Pa
12-9. a) v1 = 1,5 m/s; v2 = 6 m/s b) 16875 Pa c) 0,136 m
12-10. 0,141 mm
12-11. a) v1 = 1,019 m/s; v2 = 6,367 m/s b) 98,5 cm c) 244 litros/s
12-12. a) [2,g,h]½ b) PATM - ρ . g . hBC c) hBC ≤ Patm/ρ. g
12-13. a) vB = 0,577 m/s ; vA = vC =1,154 m/s b) PA = PC = 0; PB = 500 Pa
12-14. a) 4 m b) 1 m
BIBLIOGRAFIA:
La bibliografía utilizada para confeccionar estas prácticas es la siguiente:
Física Universitaria. 11 Edición, Volumen 1. Francis W. Sears, Mark W. Zemansky, Hugh D. Young
y Roger A. Freedman.
Física para la ciencia y la tecnología. 5ª Edición, Volumen 1 A y B. Paul A. Tipler y Gene Mosca.
Fundamentos de Física. 6ª Edición. Volumen 1, Raymond A. Serway y Jerry S. Faughn.
Física General. 32 Edición, Tomo 1. S. Burbano de Ercilla, E Burbano García y C. Gracia Muñoz.
Fuentes varias de Internet.
4° Parte: Prácticas N° 10, 11 y 12
60
FÍSICA I