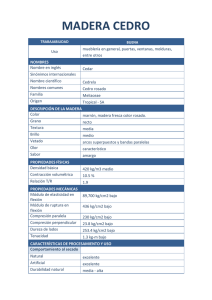
Calculo de Vigas - Estructuras Farez – Lozada – Langer

Taller Vertical de Estructuras Villar-Farez-Lozada - Nivel: 2
TP Nº6: Ejemplo de calculo de viga
placa simplemente apoyada
Elaboración: Arq. Mabel Loscalzo
Ing. Valeria Taus
Ejemplo 1: viga placa L, simplemente apoyada
1) Datos:
Viga de HºAº simplemente apoyada, sección L.
σ'bk: 170 kg/cm2 = 17 MPa (Resistencia característica)
Hormigón: H-17
σ'bc: 140 kg/cm2 (tensión característica de cálculo)
Acero: ADN 420: σek: 4200 kg/cm2 (tensión de fluencia)
υ = 1,75 (coeficiente de seguridad)
Altura total de la losa: ho = 9cm
Acción de L1 sobre V1: qL = 800 kg/m
q = 1400 kg/m
Carga de muro superior: qm = 600kg/m
Planta
Esquema isostático
1
2) Predimensionado
En vigas simplemente apoyadas h = L/10 = 3,7 m/10 = 37 cm
Adoptando h = 37 cm y un recubrimiento de 3 cm, tendremos
ht = h + rec. = 37 cm + 3 cm = 40 cm
Tomamos b0 = 12 cm (se adopta este valor de manera de ocultar la viga en los muros)
be=b0+4,5.h0=12 cm + 4,5.9 cm = 52,5 cm (ancho efectivo de placa)
Esquema sección transversal
3) Análisis de cargas y caculo de solicitaciones
Peso propio: qpp = γHº .b0. ht = 2400 kg/m3 . 0,12 m . 0,40 m =115,2 kg/m
qtotal = qpp + qL+ qm = 115 kg/m + 800 kg/m + 600 kg/m = 1515 kg/m
q
⋅ L 1515kg / m ⋅ 3,7m
total
R =R =
=
= 2803kg
B
A
2
2
q
⋅ L2 1515kg / m ⋅ (3,7m)2
total
M
=
=
= 2593kg.m
maxTramo
8
8
Diagramas
Q
M
2
4) Calculo de la armadura de flexión
En vigas placa de sección L, el brazo de palanca z = h-h0/2 = 3 cm-9cm/2 = 32,5 cm = 0,325m
M max ⋅υ
2593kg.m ⋅1,75
=
= 3,32cm 2
kg
z ⋅σ
0,325m ⋅ 4200
ek
cm 2
Aº nec =
Adoptamos 3 φ12 (A = 3,39 cm2) de los cuales levantamos en los apoyos 1φ12 (A = 1,13 cm2).
5) Verificación de la armadura mínima
kg
140
σ'
cm 2 = 0,74cm 2
bc
Aº
= 0,05 ⋅ b ⋅ h ⋅
= 0,05 ⋅12cm ⋅ 37cm.
0
min
σ
4200 kg
ek
Aº
adop.
= 3,39cm 2 > Aº
cm 2
min
= 0,74cm 2
verifica
6) Verificación de la profundidad del eje neutro
Para que no aparezcan tensiones de compresión en el nervio, se impone como condición que en
el instante de la rotura el eje neutro se encuentre dentro del espesor de la losa.
x=
x=
Aº nec.⋅σ
ek ≤ h
0
be ⋅ σ '
bc
3,32cm 2. ⋅ 4200 kg
52,5cm ⋅ 140 kg
cm 2 = 1,89cm ≤ 9cm
cm 2
x = 1,89cm ≤ 9cm verifica
7) Cálculo de la armadura de corte
Tensión de corte máxima
2803kg
=
= 7,2 kg
τ max = Qbmax
⋅ z 12cm ⋅ 32,5cm
0
cm 2
De los 3 φ12 (A = 3,39 cm2) colocados como armadura de flexión, levantamos en la zona de los
apoyos 1φ12 (A = 1,13 cm2) para que colabore tomando parte del corte solicitante.
Para calcular dicha colaboración ingresamos a la Tabla de
σek=4200
Ts,
correspondiente al acero de
kg/cm2, con el diámetro de la barra de 12 mm y ubicándonos en la columna
correspondiente al nº de barras dobladas a 45º, encontramos que la fuerza que toma dicha barra
es de 3825kg.
En el caso de una viga simplemente apoyada con carga uniformemente distribuida, la distancia
xm a la cual Q=0 resulta:
xm=L/2=3,7m/2=1,85m
3
La tensión absorbida por las barras dobladas será:
2 ⋅ 7,2 kg
⋅ 3825kg
cm 2
= 5 kg 2
185cm ⋅ 12cm
cm
τ s = 2 ⋅τ max ⋅ Ts =
xm ⋅ b0
La tensión que deberá ser absorbida por los estribos (τb) sería lo que falta para completar los
7,2 kg/cm2, es decir:
τ max = τ s + τ b
τ b = τ max − τ s = 7,2 kg
⇒
kg
kg
−
=
5
2
,
2
cm 2
cm 2
cm 2
Por otro lado se debe cumplir:
τ b min = τ max =
7,2 kg
2
2
cm 2 = 3,6 kg
cm 2
De la Tabla correspondiente a τb para estribos de φ6, entrando con un ancho de viga de 12 cm,
necesito una separación de 30 cm para cubrir los 3,6 kg/cm2 (mayor valor entre τb y τb min).
Por otro lado, debe verificarse además que la separación adoptada entre estribos resulte como
máximo:
S max =
ht 40cm
=
= 20cm
2
2
Por lo tanto adoptamos un estribado de φ6 con una separación de 20 cm.
4
8) Armado y despiece de armaduras
Despiece
Armadura sección transversal
5
Taller Vertical de Estructuras Villar-Farez-Lozada - Nivel: 2
TP Nº6: Ejemplo de calculo de viga
continua rectangular
Elaboración: Arq. Mabel Loscalzo
Ing. Valeria Taus
Ejemplo 2: viga continua rectangular V1 y V2
1) Datos:
Viga continua de HºAº, sección rectangular.
σ'bk: 170 kg/cm2 = 17 MPa
Hormigón: H-17
σ'bc: 140 kg/cm2
Acero: ADN 420: σek: 4200 kg/cm2
υ = 1,75
Acción de L1 sobre V1-V2: qL = 360 kg/m
Carga de muro superior: qm = 540kg/m
q = 900 kg/m
Planta.
Esquema hiperestático.
6
Detalle de losa prefabricada
2) Predimensionamiento
En vigas continuas h = L/15 = 3,5 m/15 = 23 cm
Adoptando h = 27 cm y un recubrimiento de 3 cm, tendremos
ht = h + rec. = 27 cm + 3 cm = 30 cm, suponiendo h = 2.b → b = 15 cm
3) Cáculo de solicitaciones:
Peso propio: qpp = γHº .b. ht = 2400 kg/m3 . 0,15 m . 0,30 m =108 kg/m
qtotal = qpp + qL+ qm = 108 kg/m + 360 kg/m + 540 kg/m = 1008 kg/m ≈ 1,01t/m
Se tiene una viga hiperestática de dos tramos. Para calcular las solicitaciones es necesario
recurrir a soluciones aproximadas mediante el empleo de coeficientes. Para ello utilizaremos las
expresiones dadas para viga continua de dos tramos del apunte “Tablas”.
q
⋅L
Reacciones: R = total
γ
1,01t / m ⋅ 3,5m
RA =
= 1,3t
2,7
RB =
1,01t / m ⋅ 3,5m
= 4,4t
0,8
RC =
1,01t / m ⋅ 3,5m
= 1,3t
2,7
7
Momentos:
M max T
ramo
qtotal ⋅ L2
=
,
β
M Apoyo
qtotal ⋅ L2
=−
α
MA =0
1,01t / m ⋅ (3,5m )2
= 1,12t.m
M max T =
11
1
1,01 / m ⋅ (3,5m )2
MB = −
= −1,55t.m
8
1,01t / m ⋅ (3,5m )2
= 1,12t.m
M max T =
11
2
MC = 0
Diagramas
Q
M
4) Cálculo de la armadura de flexión
En secciones rectangulares el brazo de palanca z = 0,9.h = 0,9.0,27 m = 0,243 m
Tramos
Aº necT = Aº necT =
1
2
M max T ⋅ υ
1120kg.m ⋅ 1,75
=
= 1,92cm 2
z ⋅ σ ek
0,243m ⋅ 4200 kg 2
cm
8
Se adoptan 4 φ8 (A = 2 cm2), de los cuales se levantan en apoyos 2 φ8 (A = 1 cm2),
Apoyo
Mcalculo=0,9.Mapoyo=0,9.1550kg.m=1395kg.m
Aº nec Apoyo =
1395kg.m ⋅ 1,75
M ⋅υ
=
= 2,39cm 2
z ⋅ σ ek 0,243m ⋅ 4200 kg
cm 2
En el apoyo intermedio hay 2 φ8 (A = 1 cm2) provenientes del Tramo 1 y 2 φ8 (A = 1 cm2)
provenientes del Tramo 2, que hacen un total de 4 φ8 (A = 2 cm2), pero según el cálculo necesito
2,39 cm2, por lo que me falta una sección de acero de 0,39 cm2. Para cubrir la sección faltante
coloco como caballete 1 φ8 (A = 0,5 cm2). En total en el apoyo quedan 5 φ8 (A = 2,5 cm2) que
cubren los 2,39 cm2 necesarios según cálculo.
5) Verificación de la armadura mínima
140 kg
Aº min = 0,05 ⋅ b ⋅ h ⋅
σ 'bc
cm 2 = 0,68cm 2
= 0,05 ⋅ 15cm ⋅ 27cm.
σ ek
4200 kg
cm 2
Aº adop.T = Aº adop.T = 2cm 2 > Aº min = 0,68cm 2
verifica
1
2
verifica
Aº adop.apoyo = 2,5cm 2 > Aº min = 0,68cm 2
6) Verificación de la profundidad del eje neutro
Como z = 0,9.h ⇒ x ≤ 0,2.h
x=
Aº nec.⋅σ ek
≤ 0,2 ⋅ h
b ⋅ σ 'bc
Apoyo: x =
2,39cm 2. ⋅ 4200 kg
15cm ⋅ 140 kg
x = 4,78cm ≤ 5,4cm
cm 2 = 4,78cm ≤ 0,2 ⋅ 27cm
cm 2
verifica
Como la profundidad del eje neutro verifica en el apoyo central, sección donde la armadura es
mayor, se deduce que también verifica en los tramos.
7) Cálculo de la armadura de corte
Tensión de corte máxima
Q
τ max = max =
b⋅z
2200kg
= 6 kg 2
15cm ⋅ 24,3cm
cm
9
En el apoyo intermedio doblamos a 45º, 2 φ8 (A = 1 cm2) a izquierda y derecha, para que
colaboren tomando parte del corte solicitante. Esta contribución la cuantificamos mediante la
Tabla de Ts.
Entrando en la Tabla correspondiente al acero de σek=4200 kg/cm2, con el diámetro de la barra
de 8 mm y ubicándonos en el nº de barras, en nuestro caso 2, encontramos que la fuerza que
pueden tomar las barras dobladas resulta de 3405 kg.
En el caso de viga continua con carga uniformemente distribuida, el corte nulo ya no se da en la
semiluz de cada tramo debido a la continuidad estructural. En este caso particular debemos
calcular la distancia xm del siguiente modo:
(1,3 t + 2,2 t)
3,5m
xm =
⇒
xm
2,2t
2,2t ⋅ 3,5m
= 2,2m
3,5t
La tensión absorbida por las barras dobladas resultará:
2 ⋅ 6 kg
⋅ 3405kg
cm 2
= 3,5 kg 2
220cm ⋅ 15cm
cm
2 ⋅ τ max ⋅ Ts
=
τs =
xm ⋅ b
La tensión que deberá ser absorbida por los estribos será la restante hasta cubrir los 6 kg/cm2, es
decir:
τ max = τ s + τ b
τ b = τ max − τ s = 6 kg
⇒
kg
kg
−
3
,
5
=
2
,
5
cm 2
cm 2
cm 2
Por otro lado se debe cumplir:
τ b min =
τ max
2
6 kg
=
cm 2 = 3 kg
2
cm 2
De la Tabla correspondiente a τb para estribos de φ6 entrando con un ancho de viga de 15 cm
para cubrir los 3 kg/cm2 (mayor valor obtenido entre τb y τb min), necesito una separación entre
estribos de 30 cm.
Debe verificarse además que la separación adoptada entre estribos resulte como máximo:
10
h 30cm
S max = t =
= 15cm
2
2
Por lo tanto adoptamos un estribado de φ6 con una separación de 15 cm.
8) Armado y despiece de armaduras
Detalle longitudinal
Obs: en apoyo intermedio: 2 φ8 a 45º de V1 + 2 φ8 a 45º de V2 + 1 φ8 (caballete) = 5 φ8.
Despiece
Detalle transversal
11