Campana de Gauss

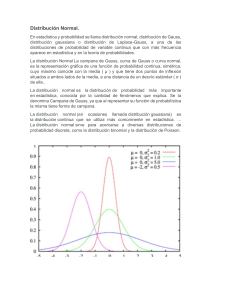
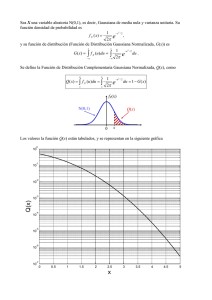
Campana de Gauss
Una variab le
a leato r ia
c o n tin u a , X,
sigue
una
d istrib u c ió n
no rmal de med i a
μ y d esviac ió n típ ic a σ , y se designa po r N( μ, σ) , si se cumple n la s sigu ientes
condicion es:
1. L a va ria bl e pued e to ma r cua lquier va lor: ( - ∞, +∞) 2. L a fu n c ió n d e d en sid ad , es
la expres ión en té rmino s de ecua ción ma temá ti ca de la c amp an a d e G au ss :
Camp an a d e G au ss
El ca mpo de existenc ia es cua lquier va lor ,
es deci r: (-∞, +∞).
Es simétr ica res pecto a la med ia µ .T iene un
má ximo en la media µ . C rece ha sta la media µ y
decrece a pa rt ir de el la .
En los puntos µ − σ y µ + σ presenta puntos
de infl exión.
El eje de a bscisa s es un a a síntota de la curva .
E l área d el r ecinto det ermina do por la funció n y eje
de a bscisa s es ig u al a la u n id ad .
A l ser simét ric a r espec to a l eje que pa sa por x = µ,
deja un á rea ig u al a 0. 5 a la izq u ierd a y o tra
ig u al a 0. 5 a la d erec h a .
La p ro b ab ilid ad eq u iv ale a l á rea en c errad a b aj o
la c u rva.
p(μ - σ < X ≤ μ + σ ) = 0.6826 = 68.26 %
p(μ - 2σ < X ≤ μ + 2σ ) = 0.954 = 95.4 %
p(μ - 3σ < X ≤ μ + 3σ ) = 0.997 = 99.7 % Y
Función gaussiana
Curvas gaussianas con distintos parámetros.
Forma tridimensional.
En estadística, la función gaussiana (en honor a Carl Friedrich
Gauss) es una función definida por la expresión:
donde a, b y c son constantes reales (a > 0).
Las
funciones
gaussianas
se
en estadística correspondiendo, en el
utilizan
frecuentemente
caso de que a sea igual a , a la función de densidad de una variable aleatoria con distribución
normal de media μ=b y varianza σ2=c2.
Propiedades
Las gaussianas se encuentran entre las funciones elementales, aunque no poseen primitivas
elementales. Sin embargo, el valor exacto de la integral impropia sobre todo el rango real
puede derivarse a partir del valor de la integral de Gauss obteniéndose que:
El valor de la integral es 1 si y solo si
la función
de
densidad de
normal de media μ=b y varianza
σ2=c2.
, en cuyo caso la función gaussiana es
una
variable
aleatoria con distribución
Se muestran varias gráficas de funciones gaussianas
en la imagen adjunta.
Las funciones gaussianas con c2 = 2 son las autofunciones de la transformada de Fourier.
Esto significa que la transformada de Fourier de una función gaussiana no es sólo otra
gaussiana, sino además un múltiplo escalar de la función original.
La gráfica de la función es simétrica con forma de campana, conocida como campana de
Gauss. El parámetro a es la altura de la campana centrada en el punto b, determinando c el
ancho de la misma.
Porque todo tiende a infinito…
Calcular el área bajo la campana de
Gauss
La demostración de que el área entre la curva descrita por la campana de Gauss
y el eje X es 1 es hermosa. En este artículo, dejo la demostración que conozco de
este hecho. Si investigan sobre otra, otra no dudéis en comentarmela.
Introducción
La función definida de la siguiente forma:
se denomina función gaussiana y su gráfica tiene forma de
campana. Tomando ciertos valores de
y obtenemos que
esta función es la función de densidad de una variable aleatoria
normal:
Si
es una variable aleatoria que sigue una distribución normal de
media y
desviación
típica (suele
escribirse
también
de
la
forma
), entonces
Para comprobar que
dos condiciones:
tiene como función de densidad a:
es una función de densidad debemos comprobar estas
1.2.La primera condición es evidente, al ser
(por definición de desviación
típica) y por ser la exponencial siempre positiva. La comprobación de la segunda
condición consiste simplemente en el cálculo de esa integral impropia…
¿Simplemente?
Quienes no conozcan esta integral pueden intentar calcularla encontrando una
primitiva y evaluando después en
y en . Tiempo perdido. No podemos
encontrar dicha primitiva. Pero, por suerte, sí podemos calcular esa integral,
aunque no con cálculo integral de una variable sino con cálculo integral de dos
variables.
Explicación previa
Para
empezar
es
evidente
que
es
simétrica
respecto
de
la
recta
(sustituid por
y
y veréis que se obtiene el mismo
resultado). Por simplicidad para los cálculos tomaremos
y
, es decir,
la función de densidad de la conocida
integral siguiente:
. Esto es, calcularemos la
Con ello, por tanto, obtenemos una función par (simétrica respecto del eje Y),
por lo que bastará con calcular la integral entre e
y después multiplicar por
dos el resultado.
Hemos dicho que vamos a utilizar cálculo integral de dos variables.
Concretamente calcularemos una integral doble (en dos variables) y deduciremos
de ese cálculo cuánto vale la integral buscada. Para el cálculo de dicha integral
doble serán esenciales las coordenadas polares.
Cálculo de la integral
La integral doble que vamos a calcular es la siguiente:
Para ello realizamos un cambio a coordenadas polares:
Al realizar este cambio los intervalos en los que toman valores
siguientes:
Por otra parte se tiene que en polares
y
son los
, por lo que el exponente de la
exponencial quedará
. Y por realizar un cambio de variable en una integral
doble debemos multiplicar por el valor absoluto del jacobiano del cambio de
variable, que en este caso es .
Ya estamos preparados para plantear la integral:
Al quedarnos una función independiente de
obtenemos:
Calculamos dicha integral:
Obtenemos entonces la primera parte de nuestro cálculo:
Por otro lado:
Sacamos la función independiente de
respecto de :
(la segunda exponencial) de la integral
Como la integral que queda dentro es independiente de
completamente de la integral respecto de
puede sacarse
, quedando:
Obtenemos entonces un producto de dos integrales iguales simplemente
renombrando la de la segunda integral a (esto no supone ningún problema, es
simplemente un cambio de nombre de la variable). Tenemos entonces la integral
al cuadrado. Tomando el principio y el final de este paso llegamos a:
Uniendo los resultados obtenidos de estos dos pasos llegamos a:
Tomando raíces cuadradas se tiene lo siguiente:
Recordemos que la función a integrar era par, por lo que el valor de la integral
completa será el resultado de multiplicar lo obtenido por dos, es decir:
Ahora tomamos la definición inicial de la función y llegamos al resultado buscado:
Aplicación:
En un estudio de laboratorio se obtiene algunos datos de la muestra estadística y se quiere
determinar cuál es la probabilidad de que en otra muestra aparezcan aleatoriamente estas
mismas mediciones.
Consideraciones matemáticas:
Esta integral es muy importante para gran cantidad de fenómenos estadísticos y ya está
calculada en unas tablas. Hoy en día incluso ya no se emplean esas tablas sino programas de
estadística y hojas de cálculo de Excel o similares.
Lo que pasa es que todavía se considera didáctico el saber emplear esas tablas.
Bueno, vayamos a un
problema. Primero hay que decir que en la notación establecida para
esto se usa la letra sigma en vez de la alfa para la desviación estándar y en lugar de la x con
barra se emplea la letra mu.
Si se hace el cambio de variable
z=x−μσ
Se obtiene lo que se llama una distribución de probabilidad normal N (0,1) donde el 0 significa
que la media de Z es 0 y el 1 es la desviación estándar de Z
La función de distribución de Z una vez hecho el cambio de variable y sustituido la diferencial
de x por la de z es
f (z)=12π−−√e−z22
Y esa es la función de distribución para la que se han hecho las tablas de los valores que
resultan de la integración entre -infinito y un valor concreto. Con ellas se puede calcular
cualquier probabilidad de sucesos que sigan una distribución normal.
En nuestro caso tenemos
P (5.8 <= X <= 6.3)
Hacemos el cambio de variable, que en estadística se llama tipificar la distribución
Z = (X- 6.4) / 0.73
Para X=5.8 tenemos Z = (5.8-6.4)/0.73 = - 0.8219178082
Para X=6.3 tenemos Z = (6.3-6.4)/0.73 = - 0.1369863014
Luego la probabilidad es
P(- 0.8219178082 <= Z <= - 0.1369863014) =
Que se puede descomponer como
P (Z <= - 0.1369863014) - P (Z <= - 0.8219178082) =
Un problema adicional es que las tablas solo tienen valores positivos de Z, pero como la
variable aleatoria Z tiene media 0 es simétrica respecto del eje Y y se calculan así
P (Z <= - a) = 1 - P(Z<= a)
Con lo cual es
= 1 - P (Z <= 0.1369863014) - 1 + P (Z <= 0.8219178082) =
Y ahora buscaremos esas probabilidades en la tabla
Tabla (0.13) = 0.5517
Tabla (0.14) = 0.5557
Valor interpolado en (0.137) = 0.5517 +0.7 (0.0040) = 0.5545
Tabla (0.82) = 0.7939
Tabla (0.83) = 0.7967
Valor interpolado en (0.8219) = 0.7939 + 0.19 (0.7967-0.7939) = 0.794432
Y la cuenta que llevamos pendiente será
= 1 - 0.5545 -1 + 0.794432 = 0.239932
Esa es la probabilidad, 0.239932