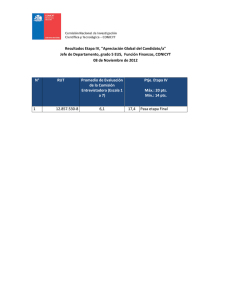
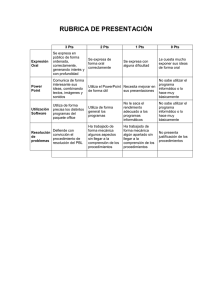
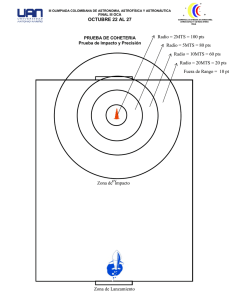
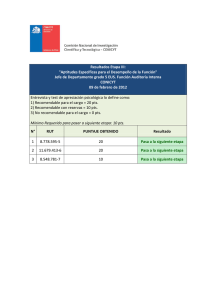
pauta_c1_ma1002_2014.. - Docencia DIM

Pauta Control 1 Propuesta Ejercicios - MA1002 Cálculo Diferencial e
Integral
Escuela de Ingeniería, FCFM, U. de Chile. Semestre 2014-1
P1) Considere la función f definida por


cos x − 1 , si x < 0
f (x) = ax2 + b
, si 0 ≤ x ≤ 1


2x − 1
, si x > 1
a) Encuentre los valores de las constantes a y b, si existen, para que f sea una
función continua en R. Justifique su respuesta.
(3 pts.)
b) Determine si f es derivable en x = 0 y x = 1. En caso de que sea posible,
calcule f 0 (0) y f 0 (1). Justifique su respuesta.
(3 pts.)
Solución
a) Veamos la continuidad en x = 0. luego
lı́m f (x) = lı́m− cos x − 1 = 0,
x→0−
x→0
(0.5 pts.)
además
lı́m f (x) = lı́m− ax2 + b = b.
x→0+
x→0
(0.5 pts.)
Luego f es continua en x = 0 si y sólo si b = 0.
(0.5 pts.)
Por otra parte, para la continuidad de f en x = 1 se tiene que
lı́m f (x) = lı́m ax2 = a,
x→0−
x→1−
(0.5 pts.)
y además
lı́m f (x) = lı́m 2x − 1 = 1.
x→0−
x→1+
(0.5 pts.)
Por lo tanto f es continua en x = 0 si y sólo si a = 1.
(0.5 pts.)
b) Veamos la derivada en x = 0.
lı́m−
h→0
(cos h − 1) − 0
cos h − 1
f (h) − f (0)
= lı́m−
= lı́m−
= 0.
h
h
h
h→0
h→0
(0.5 pts.)
además
lı́m+
h→0
f (h) − f (0)
h2 − 0
= lı́m+
= lı́m+ h = 0.
h
h
h→0
h→0
(0.5 pts.)
Luego f es derivable en x = 0 y además f 0 (0) = 0.
(0.5 pts.)
1
Veamos la derivada en x = 1.
lı́m
h→0−
f (1 + h) − f (1)
(h + 1)2 − 1
h2 + 2h
= lı́m
= lı́m
= 2.
h
h
h
h→0−
h→0−
(0.5 pts.)
además
lı́m
h→0+
f (1 + h) − f (1)
(2(h + 1) − 1) − 1
= lı́m
= lı́m 2 = 2.
h
h
h→0+
h→0+
(0.5 pts.)
Luego f es derivable en x = 1 y además f 0 (1) = 2.
(0.5 pts.)
2
P2)
a) Sea f : [a, b] → R una función continua. Pruebe que f ([a, b]) es un intervalo
cerrado en R, es decir, f ([a, b]) = [c, d], con c, d ∈ R.
(3 pts.)
b) Sea f
:
R
→
R una función continua. Supongamos que
f (0) = f (1) = 0 y f es estrictamente creciente en el intervalo (0, 41 ). Pruebe que para todo x ∈ (0, 14 ), existe al menos un y ∈ [0, 1], con x 6= y, tal que
f (x) = f (y).
(3 pts.)
Solución
a) Notemos que dado que f es continua en el intervalo cerrado [a, b], entonces el
máximo y el mínimo se alcanzan en dicho intervalo, es decir, existen x, y ∈ [a, b]
tales que para todo z ∈ [a, b].
f (x) ≤ f (z) ≤ f (y).
(1 pts.)
Sean c = f (x) y d = f (y). Por lo tanto se tiene que
f ([a, b]) ⊂ [c, d].
(1 pts.)
Veamos que [c, d] ⊂ f ([a, b]). En efecto, es claro que c, d ∈ f ([a, b]), además si
r ∈ [c, d], entonces tenemos que
c = f (x) ≤ r ≤ f (y) = d.
así del Teorema del valor intermedio debe existir z0 ∈ [a, b] tal que r = f (z0 ),
lo que prueba la doble inclusión y por lo tanto f ([a, b]) = [c, d].
(1 pts.)
1
4 ),
luego como f es creciente estrictamente en el intervalo (0,
b) Sea x ∈ (0,
tiene que r = f (x) > 0. Notemos que luego se tiene que
1
4)
se
1
0 < r < f( )
4
(1 pts.)
o equivalentemente
1
f (1) < r < f ( ).
4
(1 pts.)
así como f es continua en ell intervalo [0,1] y del Teorema del Valor Intermedio
se tiene que existe y ∈ ( 14 , 1) tal que f (x) = r = f (y), lo que completa la
demostración.
(1 pts.)
3
P3)
a) Consideremos la función f : R → R, una función derivable en R. Definamos la
función
g(x) = f (xf (2x))
1) Encuentre la derivada de g en términos de la derivada de f .
(4 pts.)
2) Suponiendo que f (0) = 1 y f 0 (0) = 2, calcule g 0 (0).
(2 pts.)
Solución
1.
a) Usando la regla de la cadena se tiene que
g 0 (x) = f 0 (xf (2x)) · {f (2x) + xf 0 (2x) · 2} = f 0 (xf (2x)) · {f (2x) + 2xf 0 (2x)}
(4 pts.)
b) De la parte anterior se tiene que
g 0 (0) = f 0 (0f (0)) · {f (0) + 0 · f 0 (0)} = f 0 (0) · {f (0) + 0} = 2 · 1 = 2.
(2 pts.)
4