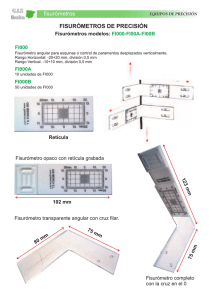
Separacion de la parte radial y angular

Obtención de Φ(R) mediante separación en parte radial y
angular
Dado que el operador energia potencial depende unicamente de la
distancia internuclear, resulta ventajoso el uso de coordenadas
esfericas para solucionar la ecuación diferencial (3D). De manera que
h2 2
ˆ
∇ R + U k ( R) ⇒
H int = −
2µ
 1 ∂  2 ∂  1  ∂2
∂
1 ∂ 2 
 + U k ( R) =
+
R
 + 2  2 + cot θ
 2
2
2 
∂
∂
∂
∂
∂
θ
θ
θ
ϕ
R
R
R
R
sin





1 ˆ2
h2 1 ∂  2 ∂ 
=−
L
R
 + U k ( R) +
2
2 µ R ∂R  ∂R 
2 µR 2
h2
⇒−
2µ
La parte angular de la expresion de la Laplaciana en coordenadas
esfericas corresponde a la forma que tiene el operador L2 para el
rotor rígido y es separable de la parte radial.
Por tanto, la función de onda correspondiente se puede separar de
manera exacta en una contribución radial y parte angular
Φ n ( R, θ , ϕ ) ⇒ S ( R)ΥJmJ (θ , ϕ )
Puesto que se cumple que [Hint,L2]=[Hint,Lz] = 0, las funciones propias
de Hint, pueden elegirse de manera que lo sean tambien de L2 y Lz .
Dichas funciones propias son las soluciones del rotor rígido (o bien
particula en la superficie de una esfera); son los llamados armónicos
esféricos .
Lˆ2 ΥJmJ (θ , ϕ ) = J ( J + 1)h 2 ΥJmJ (θ , ϕ )
Lˆ z ΥJmJ (θ , ϕ ) = ± m J hΥJmJ (θ , ϕ )
Aparecen dos números cuánticos, J y mJ , que restringen el valor de
17
la magnitud del momento angular de rotación total y su proyección
sobre el eje Z, respectivamente.
Al aplicar Hint sobre Φ(R,θ,φ) , teniendo en cuenta la separación de la
parte radial y angular y que la parte angular es función propia de L2,
se obtiene
Hˆ int S ( R ) Υ Jm J (θ , ϕ ) = ε int S ( R )Υ JmJ (θ , ϕ )
 h2 1 ∂  2 ∂ 

 S ( R )ΥJmJ (θ , ϕ ) +
 −
R
+
U
R
(
)


k
2
 2 µ R ∂R  ∂R 

1 ˆ2
+
L S ( R )ΥJmJ (θ , ϕ ) = ε int S ( R)ΥJmJ (θ , ϕ )
2
2 µR
⇓
 h2 1 ∂  2 ∂ 
J ( J + 1)h 2 
 −
 S ( R ) = ε int S ( R )
R
 + U k ( R) +
2
∂
∂
2
µ
R
R
R
2
µ




donde se ha eliminado finalmente la parte angular para obtener la
expresión de la dependencia radial de la ecuación.
Definiendo una nueva función de la forma
F ( R ) = S ( R) R se
simplifica la ecuación anterior ya que
d 2 F ( R)
= S ( R )' ' R + 2 S ( R)'
dR 2
dF ( R)
= S ( R )' R + S ( R)
dR
y dado que el resultado de aplicar la primer contribución del operador
es
1 ∂  2 ∂ 
1 d  2 dS ( R ) 
R
S ( R) = 2
R
=
2
R ∂R  ∂R 
R dR 
dR 
1
F ( R)' '
= 2 2 R S ( R )'+ R 2 S ( R )' ' =
R
R
(
)
18
la ecuación final se puede escribir de la forma
J ( J + 1)h 2  F ( R )
F ( R)
h 2 F ( R )' ' 

−
+ U k ( R) +
= ε int
2
2µ R
2 µR
R

 R
⇓

J ( J + 1)h 2 
h2

 F ( R ) = ε int F ( R )
F ( R)' '+ U k ( R) +
−
2
2µ
µ
2
R



J ( J + 1)h 2 
 representa el potencial efectivo en el
La expresión U k ( R ) +
2 µR 2 

que se mueven los núcleos, que contiene un nuevo término de
carácter repulsivo
J ( J + 1)h 2
> 0 debido a la rotación de la molécula
2 µR 2
(potencial centrífugo)
19