Dispositivos Cilindro-Pistón

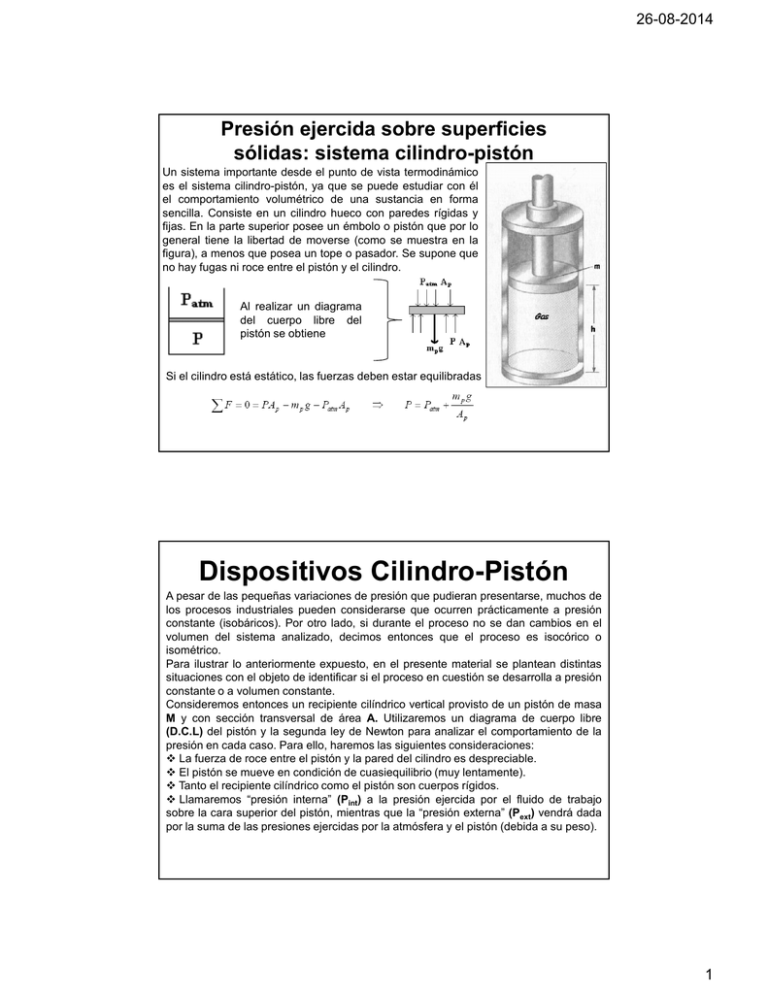
26-08-2014
Presión ejercida sobre superficies
sólidas: sistema cilindro-pistón
Un sistema importante desde el punto de vista termodinámico
es el sistema cilindro-pistón, ya que se puede estudiar con él
el comportamiento volumétrico de una sustancia en forma
sencilla. Consiste en un cilindro hueco con paredes rígidas y
fijas. En la parte superior posee un émbolo o pistón que por lo
general tiene la libertad de moverse (como se muestra en la
figura), a menos que posea un tope o pasador. Se supone que
no hay fugas ni roce entre el pistón y el cilindro.
Al realizar un diagrama
del cuerpo libre del
pistón se obtiene
Si el cilindro está estático, las fuerzas deben estar equilibradas
Dispositivos Cilindro-Pistón
A pesar de las pequeñas variaciones de presión que pudieran presentarse, muchos de
los procesos industriales pueden considerarse que ocurren prácticamente a presión
constante (isobáricos). Por otro lado, si durante el proceso no se dan cambios en el
volumen del sistema analizado, decimos entonces que el proceso es isocórico o
isométrico.
Para ilustrar lo anteriormente expuesto, en el presente material se plantean distintas
situaciones con el objeto de identificar si el proceso en cuestión se desarrolla a presión
constante o a volumen constante.
Consideremos entonces un recipiente cilíndrico vertical provisto de un pistón de masa
M y con sección transversal de área A. Utilizaremos un diagrama de cuerpo libre
(D.C.L) del pistón y la segunda ley de Newton para analizar el comportamiento de la
presión en cada caso. Para ello, haremos las siguientes consideraciones:
La fuerza de roce entre el pistón y la pared del cilindro es despreciable.
El pistón se mueve en condición de cuasiequilibrio (muy lentamente).
Tanto el recipiente cilíndrico como el pistón son cuerpos rígidos.
Llamaremos “presión interna” (Pint) a la presión ejercida por el fluido de trabajo
sobre la cara superior del pistón, mientras que la “presión externa” (Pext) vendrá dada
por la suma de las presiones ejercidas por la atmósfera y el pistón (debida a su peso).
1
26-08-2014
Dispositivos Cilindro-Pistón
1er caso: el pistón se encuentra inicialmente en equilibrio
en el estado inicial (1). Se transfiere calor al fluido y el
pistón se eleva lentamente hasta llegar al estado final (2).
El D.C.L. es el mismo en la posición inicial (1), en la posición final (2) y en cualquier
posición intermedia del pistón, siendo la presión interna igual a la presión externa
(ec.I). En vista que ni la presión atmosférica ni el peso del pistón varían durante el
proceso y que el pistón se mueve en condición de cuasiequilibrio, se puede decir que
el proceso ocurre a presión constante.
Dispositivos Cilindro-Pistón
2do caso: el pistón se encuentra inicialmente descansando
sobre unos topes inferiores en el estado inicial (1). Se
transfiere calor al fluido y el pistón se eleva lentamente
hasta llegar al estado final (2).
2
26-08-2014
Dispositivos Cilindro-Pistón
Según la ec. II, la presión interna inicial es menor que la
presión externa (constante), por lo cual el pistón no
comenzará de inmediato a moverse. A medida que la
presión interna aumente, la presión ejercida por los topes
(Ptopes) irá disminuyendo debido a la tendencia del pistón
a despegarse de los mismos. En el momento en que el
pistón se ha separado infinitesimalmente de los topes
(Ptopes = 0), el D.C.L. de éste será exactamente igual al
obtenido para el 1er caso, por lo cual de ahí en adelante
el movimiento del pistón será idéntico al ya explicado
anteriormente.
Dispositivos Cilindro-Pistón
3er
caso: el pistón se encuentra inicialmente en equilibrio
en el estado inicial (1). Se transfiere calor al fluido y el
pistón se eleva lentamente hasta que toca los topes
superiores. Se sigue calentando hasta que el fluido llega
al estado final (2).
En la ec. III se observa que el pistón en el estado inicial (1) comenzará de una vez a
moverse ya que las presiones interna y externa son iguales entre sí. Tal como se
explicó para el 1er caso, el pistón se desplazará a presión constante hasta encontrarse
a una separación infinitesimal de los topes superiores (Ptopes = 0). Al seguir calentando,
la presión interna aumentará por lo que los topes deben ejercer presión sobre el pistón
para que éste se mantenga en la misma posición.
3
26-08-2014
Dispositivos Cilindro-Pistón
3er caso:
Según la ec. IV, la presión interna final es mayor que
la presión externa (constante), por lo cual el pistón
una vez que haya tocado los topes experimentará un
proceso a volumen constante. Obviamente esta
condición se mantendrá hasta que los topes alcancen
su presión máxima posible, en cuyo caso éstos
podrían romperse al cabo de cierto tiempo.
Resumen
A continuación se presentan los casos típicos que se encuentran en un sistema
cilindro-pistón:
b) Intercambio de calor (velocidad del
pistón constante)
a) pistón sin movimiento
c) Topes inferiores
e) Resorte
d) Topes superiores
f) horizontal
4
26-08-2014
Las variables termodinámicas o variables de estado
•
Temperatura (T): es una medida del calor o energía térmica de las
partículas en una sustancia y no depende del tamaño o tipo de objeto.
Cuando trabajemos con relaciones de temperatura, por ejemplo, T1/T2 estas siempre
deben estar en escala absoluta, es decir, en Kelvin o Rankine. En el caso de restas,
pueden ser en cualquier escala.
Ejemplo:
Entre 25°C y 80°C, determine la relación de temperaturas T 1/T2 y
la variación T2 - T1
Escala de temperatura
Para establecer una escala de temperatura, se seleccionan dos puntos de
referencia:
El punto de congelación, la temperatura a la que se encuentran en
equilibrio una mezcla de hielo y agua saturada de aire, bajo una presión de 1
atm.
El punto de ebullición, la temperatura de equilibrio para el agua pura y su
valor, bajo una presión de 1 atm.
Existen dos escalas de temperaturas de uso generalizado:
Escala Celsius: asigna una valor de 0°C al punto de congelación del agua
saturada con aire a presión atmosférica estándar y de 100°C a l punto de
ebullición del agua pura a presión atmosférica estándar.
Escala Fahrenheit: asigna una valor de 32°F al punto de fusión de una
mezcla de sales con hielo (0°F) y de 212 °F al punto de ebullici ón del agua
T ( ° F ) = 1 , 8 T ( ° C ) + 32
T ( ° F ) = T ( ° R ) − 459 , 67
5
26-08-2014
Escala absoluta de temperatura
Existen dos escalas absolutas de temperaturas de uso generalizado:
Escala Kelvin: se basa en los principios de la termodinámica en los que
predice la existencia de una temperatura mínima, en la cual, las partículas de
un sistema carecen de energía térmica. La temperatura en la cual las
partículas carecen de movimiento se conoce como cero absoluto (0°K)
Escala Rankine: se define midiendo en grados Fahrenheit sobre el cero
absoluto, por lo que se carece de valores negativos
T ( ° K ) = T ( ° C ) + 273 ,15
T ( ° R ) = T ( ° F ) + 459 , 67
T ( ° R ) = 1 ,8 T ( ° K )
Equilibrio Térmico
Es el estado en el que se igualan las temperaturas de dos cuerpos que
inicialmente tenían diferentes temperaturas. Al igualarse las temperaturas se
suspende el flujo de calor, y el sistema formados por esos cuerpos llega a
su equilibrio térmico.
Por ejemplo, si pone tienes un recipiente con agua caliente, y otro con agua
fría, a través de sus paredes se establecerá un flujo de energía calorífica,
pasado un tiempo, la temperatura del agua en ambos recipientes se igualará
(por obra de las transferencias de
calor, en este caso del agua más
caliente a la más fría, también por
contacto con el aire del medio
ambiente y por evaporación), pero
el equilibrio térmico lo alcanzarán
cuando ambas masas de agua
estén a la misma temperatura.
6
26-08-2014
Ley cero de la termodinámica
La ley cero esta basada en la existencia de dos cuerpos, uno caliente y uno
frio, ambos se ponen en contacto. Si además se aíslan del entorno, el cuerpo
caliente se enfría, mientras que el frio se calienta. Así las propiedades se
mantiene invariables con el tiempo, al alcanzar el equilibrio térmico.
Por otro lado si un tercer cuerpo se pone en contacto térmico con cualquiera
de ellos y todas sus propiedades permanecen sin cambiar, se dice que los
tres cuerpos están en equilibrio térmico entre si.
“Si dos cuerpos están en equilibrio térmico con un tercero, los tres están
en equilibro térmico entre si”
Ejemplo: estufa de los pobres
GASES
GASES IDEALES
7
26-08-2014
GAS
Los gases son sustancias que se caracterizan porque sus
moléculas se mantienen en desorden, dotadas de alta energía
(están en constante movimiento) y separadas por “grandes”
distancias donde la interacción intermolecular es casi nula. Los
gases no poseen volumen ni forma determinada, es decir, que a
diferencia de los sólidos y los líquidos, ocupan todo el volumen
del recipiente que los contiene, adopta la del recipiente que lo
contiene
Variables del gas
La temperatura es un propiedad
física de los gases. A temperaturas
altas sus moléculas se mueven más
rápido. La temperatura se debe
expresar en Kelvin K = °C + 273.
El Volumen (V) es el espacio
ocupado por un gas. El gas es
compresible y su volumen estará
determinado
por
el
espacio
ocupado. Si un gas se comprime, su
presión y volumen
se modificarán de
acuerdo a las leyes
de los gases.
es una fuerza que se ejerce sobre una
superficie. La presión de un gas está
relacionada con el número de choques
por unidad de tiempo de las moléculas
del gas contra las paredes del recipiente.
Cuando la presión aumenta quiere decir
que el número de choques por unidad de
tiempo es mayor.
8
26-08-2014
Variables del gas
Su unidad es el mol. Un mol es la cantidad de sustancia que contiene tantos
átomos o moléculas como hay precisamente en 12 g. de Carbono 12, o bien
un mol es aquel numero de gramos de una sustancia numéricamente igual a la
masa molecular de la sustancia.
La relación entre temperatura, presión, volumen y la cantidad de gas
expresado en moles, se las conoce como LEYES DE LOS GASES estas se
basan en cuatro variables para definir la condición física o estado del gas tales
son: temperatura, presión, volumen y cantidad de gas expresado en moles
VOLUMEN (L)
CANTIDAD DE
MOLES (n)
GASES
TEMPERATURA (T)
PRESION (P)
GAS IDEAL
Un gas ideal es aquel constituido por un número grande de moléculas
puntuales que están en movimiento aleatorio y a distancias
suficientemente grandes para que interaccionen únicamente durante los
choques. Los choques de las moléculas se consideran perfectamente
elásticos. A muy bajas presiones (menores a 10 atmlos gases se
aproximan al comportamiento ideal (sin importar la temperatura). Los
gases se desvían del comportamiento de gas ideal principalmente cuando
están cercanos al punto crítico (Es el estado donde las fases líquida y
gaseosa se confunden)
Los gases ideales se rigen por la ecuación de los gases ideales.
9
26-08-2014
Existen 4 leyes de los gases ideales
Ley de Boyle
Ley de Gay-Lussac
Formulada
por
Robert
Boyle
y
Edme
Mariotte
Ley de Charles
Formulada
por Jacques
Alexandre
César
Charles
Formulada
por JosephLouis GayLussac
Ley de Avogadro
Formulada
por Lorenzo
Romano
Amedeo
Carlo
Avogadro
Ley de Boyle (Isotérmica)
Cuando el volumen y la presión de una cierta cantidad de gas es mantenida a
temperatura constante, el volumen será inversamente proporcional a la presión
A Menor presión,
mayor volumen.
A Mayor presión,
menor volumen.
10
26-08-2014
Ley de Charles (Isométrica)
El volumen de una cantidad fija de gas mantenida a presión constante es
directamente proporcional a su temperatura absoluta.
A mayor temperatura, mayor volumen.
Ley de GayGay-Lussac (Isobárica)
La presión de un gas que se mantiene a volumen
constante, es directamente proporcional a la
temperatura
Cuando sometemos un gas a un calentamiento y lo
dejamos que se expanda libremente, el volumen se
incrementara proporcionalmente con el incremento
de la temperatura, pero su presión no se altera,
pues siempre será ejercida por la atmosfera y por el
objeto o por la sustancia que funcione como tapón
hermético.
A
mayor
temperatura,
mayor presión.
11
26-08-2014
Ley de Avogadro
El físico italiano Amadeo Avogadro, formuló en 1811 una hipótesis para el
numero de moléculas de un gas confinado en un recipiente; para demostrarlo,
se toman dos porciones de gases diferentes y se colocan en dos recipientes
de igual volumen a la misma temperatura y presión y el numero de moléculas
de cada recipiente debe ser el mismo.
“Volúmenes iguales de gases diferentes a la
misma presión y temperatura, contienen el
mismo numero de moléculas”
Numero de avogadro
Para volúmenes iguales de gases diferentes en condiciones normales de
presión y temperatura (1atm y 273K) , el numero de molécula es 23x1023 por
cada mol de cualquier gas.
p
T
n
V
Boyle
aumenta
constante
constante
disminuye
V α 1/p
Charles
constante
aumenta
constante
aumenta
TαV
Avogadro
constante
constante
aumenta
aumenta
nαV
12
26-08-2014
Ecuación de estado para un gas ideal
Ecuación de estado, es la relación que existe entre dos o más propiedades
termodinámicas.
Cuando en los gases la presión es baja o la temperatura es alta, se consideran
sistemas gaseosos de baja densidad, en estas condiciones los gases se rigen
con las leyes de los gases ideales. Todos los gases a presiones relativamente
baja (menores a 10 atm) obedecen a la ecuación de gas ideal, en estas
condiciones, la presión, el volumen especifico, y la temperatura se relacionan
por la siguiente ecuación:
n = número de moles
P = presión en atmósferas (atm)
V = volumen ( lts )
v=volumen especifico
T = temperatura ( ºK)
R=constante universal de los
gases
M=Masa molar
R=
Ru
M
PV = nRuT
Pv = RT
En ocasiones la ecuación del gas ideal con frecuencia se utiliza
con las unidades de masa, en estos casos la ecuación del gas
ideal se emplea una constante especifica del gas R en vez de Ru
Ejemplo
Un neumático de automóvil que posee un volumen de 0.6 (m3), es
inflado hasta una presión manométrica de 200 (kPa). Calcule la
masa de aire en el neumático si la temperatura es de 20 (ºC) y
Raire=0,287 [kJ/kg*K]
R: Se asume que el aire se comporta como un gas ideal a las condiciones del
ejemplo. En la ecuación de gas ideal, PV = nRT, debemos utilizar la temperatura y
presión absoluta. Entonces usando Patm = 100 (kPa).
P = 200+ 100 = 300(kPa)
y
T = 20 + 273 = 293(K )
La masa puede ser calculada de la siguiente forma:
N 

 300000
 (0 . 6 m 3 )
PV
m2 

m =
=
= 2 . 14 (kg )
RT

N ⋅m
 287
 (293 K )
kg 

13