UNIVERSIDAD DE PUERTO RICO HUMACAO DEPARTAMENTO

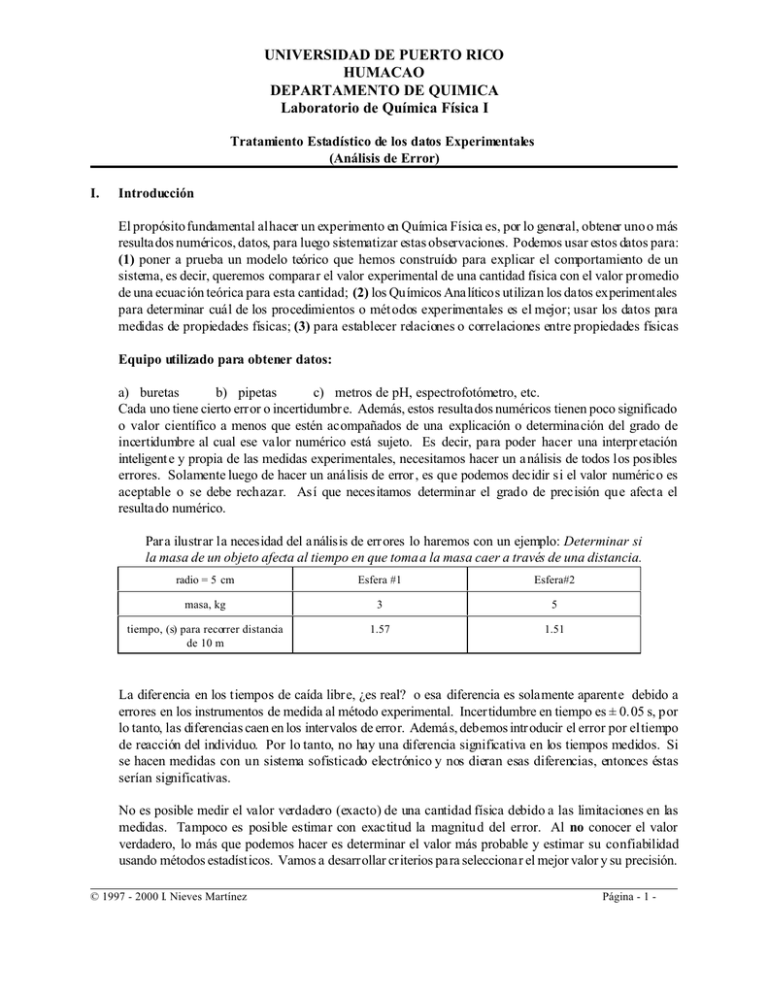
UNIVERSIDAD DE PUERTO RICO
HUMACAO
DEPARTAMENTO DE QUIMICA
Laboratorio de Química Física I
Tratamiento Estadístico de los datos Experimentales
(Análisis de Error)
I.
Introducción
El propósito fundamental al hacer un experimento en Química Física es, por lo general, obtener uno o más
resultados numéricos, datos, para luego sistematizar estas observaciones. Podemos usar estos datos para:
(1) poner a prueba un modelo teórico que hemos construído para explicar el comportamiento de un
sistema, es decir, queremos comparar el valor experimental de una cantidad física con el valor promedio
de una ecuación teórica para esta cantidad; (2) los Químicos Ana líticos utilizan los datos experimentales
para determinar cuál de los procedimientos o métodos experimentales es el mejor; usar los datos para
medidas de propiedades físicas; (3) para establecer relaciones o correlaciones entre propiedades físicas
Equipo utilizado para obtener datos:
a) buretas
b) pipetas
c) metros de pH, espectrofotómetro, etc.
Cada uno tiene cierto error o incertidumbr e. Además, estos resultados numéricos tienen poco significado
o valor científico a menos que estén acompañados de una explicación o determinación del grado de
incertidumbre al cual ese valor numérico está sujeto. Es decir, para poder hacer una interpr etación
inteligente y propia de las medidas experimentales, necesitamos hacer un análisis de todos los posibles
errores. Solamente luego de hacer un análisis de error , es que podemos decidir si el valor numérico es
aceptable o se debe rechazar. Así que necesitamos determinar el grado de precisión que afecta el
resultado numérico.
Para ilustrar la necesidad del análisis de err ores lo haremos con un ejemplo: Determinar si
la masa de un objeto afecta al tiempo en que toma a la masa caer a través de una distancia.
radio = 5 cm
Esfera #1
Esfera#2
masa, kg
3
5
tiempo, (s) para recorrer distancia
de 10 m
1.57
1.51
La diferencia en los tiempos de caída libre, ¿es real? o esa diferencia es solamente aparente debido a
errores en los instrumentos de medida al método experimental. Incertidumbre en tiempo es ± 0.05 s, por
lo tanto, las diferencias caen en los intervalos de error. Además, debemos introducir el error por el tiempo
de reacción del individuo. Por lo tanto, no hay una diferencia significativa en los tiempos medidos. Si
se hacen medidas con un sistema sofisticado electrónico y nos dieran esas diferencias, entonces éstas
serían significativas.
No es posible medir el valor verdadero (exacto) de una cantidad física debido a las limitaciones en las
medidas. Tampoco es posible estimar con exactitud la magnitud del error. Al no conocer el valor
verdadero, lo más que podemos hacer es determinar el valor más probable y estimar su confiabilidad
usando métodos estadísticos. Vamos a desarrollar criterios para seleccionar el mejor valor y su precisión.
© 1997 - 2000 I. Nieves Martínez
Página - 1 -
TRATAMIENTO ESTADÍSTICO
II. Fuentes de Error y Tipos de Errores
A. Error = diferencia entre el valor observado y el valor verdadero (aceptado) de la cantidad física
E = X ? - XV
B. Clasificación
1)
Errores sistemáticos = tiene que ver con algún desperfecto en el equipo o el método
(Determinado). No afecta la precisión de la determinación, pero sí la certeza.
2)
Errores Indeterminados = son inherentes en la observación, no se puede predecir su origen ni su
magnitud, así que no se puede eliminar, tiene signo algebraico positivo o negativo (ambos con
igual probabilidad)
DETERMINADOS (SISTEMATICO S)
INDETERMINADOS
Ejemplos:
Ejemplos:
fricción entre partes del instrumento
Cambi os en voltaje, humedad, presión atmosférica,
temperatura (Ej: Si aumenta la temperatura, el brazo de la
balanza se expande)
condiciones ambientales (humedad, temperatura)
Humanos: paralaje, lectura errónea de una escala,
reflejos lentos
Humanos: se puede leer una escala un poco más arriba o
abajo de lo verdadero sin que incluya par alaje, men isco,
reflejos
Instrumentales: falta de cali bración; ca mbio en
línea base; escape de gas en línea de vacío, no
nivelar las balanzas
Instrumentales - límite de confiabilidad del instrumento (no
hay in strument o perfect o)
Característic as:
Característic as:
Se deben a desperfectos del in strument o o la técnica
Se pueden identificar en fluctuaciones al azar en las medidas
experimentales sucesivas, afectan reproducibilidad.
Se pueden eliminar usando correcciones
No aparecen como fluctuaciones en la medida
Se pueden reducir y obedecen a la fun ción de distribución de
probabilidad de Gauss. Se usan métodos estadísticos e
interpretación probabilística.
Se pueden identificar al cambiar la técnica
experimental
III. Expresiones de confiabilidad de una medida:
A. Precisión - Reproducibilidad que reside en un resultado numérico.
incertidumbre debido a errores indeterminados.
Medida del grado de
--La precisión se puede mejorar tomando un número grande de medidas y haciendo análisis
estadísticos.
© 1997 - 2000 I. Nieves Martínez
Página - 2 -
TRATAMIENTO ESTADÍSTICO
--Si conocemos el error de una determinación lo podemos expresar como el error mismo (absoluto)
o como función de la magnitud de la medida (relativa)
Ejemplo: Pedazo de metal que mide 10.0 metros con incertidumbre de 0.5 metros. Incertidumbre
absoluta es 0.5 metros y la relativa es 0.5/10 = 0.05 metros. Si se expresa como % resulta en un
5%. Un pedazo de metal que mida 100.0 m tiene incertidumbre relativa en % de: 0.5/100.0 x 100
= 0.5%
B. Exactitud - medida o índice de cuán cerca está el valor medida del verdadero (si se conoce el real).
La podemos considerar como una experesión de la incertidumbre total.
Debido a que el valor verdadero (real) no se conoce, usaremos el promedio aritmético de una serie
de determinaciones como el valor verdadero. La diferencia entre el valor observado y el promedio
la llamamos desviación (r esiduo). Si la desviación es pequeña comparada con la magnitud de la
cantidad medida, decimos que la medida es precisa. Noten que una medida pr ecisa no es
necesariamente una medida exacta.
IV. Conceptos Estadísticos:
A. Cifras significativas en cálculos aritméticos
1)
Al sumar o restar se redondean todos los números de acuerdo con el que menos sitios decimales
tenga (i. e. el número de la incertidumbre o error absoluto mayor) antes de llevar a cabo la
operación. El resultado tendrá el mismo número de sitios decimales.
Ejemplo:
0.3442
1207.6
1.33
0.3
1207.6
1.3
La precisión en este ejemplo está limitada por 1207.6 que tiene error absoluto mayor.
2) Al multiplicar o dividir se redondean todos los números de acuerdo con el menos preciso (el de mayor
error relativo), de manera que la incertidumbre de cada número se acerque a la de este sin que llegue
a ser mayor. La misma regla se aplica al resultado.
Ejemplo:
Error Absoluto
Error Relativo
0.0024 ± 0.0001
47.61 ± 0.01
© 1997 - 2000 I. Nieves Martínez
Página - 3 -
TRATAMIENTO ESTADÍSTICO
2.83
± 0.01
La expresión redondeada correctamente:
B. Distribución de errores:
En una serie de medidas de la misma cantidad física, los resultados están distribuidos al azar
alrededor de un valor promedio. Para un número grande de medidas:
1)
los resultados que más se desvían del promedio ocurren con menos frecuencia
2)
los valores individuales están distribuidos simétricamente alrededor del promedio
donde:
y = f(x)
si )X 6 0
donde: F = desviación estándard
Noten que la probabilidad de que un valor medido tenga un valor entre x y x + dx está dado por
f (x) dx = ydx = dni/N = área bajo la curva entre x y x + dx
C. Indices de precisión y confiabilidad de las medidas
Se puede utilizar la función de distribución par a determinar cuál es la confiabilidad de cua lquiera de
las medidas: mejor valor , precisión
1)
Promedio - el mejor valor
2)
Medidas de exactitud y precisión:
_
a) * 1 = (Xi - X ) - desviación
b)
desviación promedio =
* 1 + * 2 + * 3 + .... * n = 0
© 1997 - 2000 I. Nieves Martínez
Página - 4 -
TRATAMIENTO ESTADÍSTICO
c)
1)
medida cuantitativa de la dispersión de un conjunto de medidas
2)
desventaja - hace las medidas más precisas de lo que en realidad son
desviación estándar =
Si el número de medidas es bien grande, la desviación estándar nos dice que hay una
probabilidad de 0.32 de que cualquier medida se desvíe del promedio aritmético por una o más
unidades de F
Para los casos en que hace más una sola medida, podremos estimar la incertidumbre de ésta a base de la
incertidumbre del instrumento usado para medir la cantidad física (depende de la escala del instrumento).
Si N < 3, incluyendo una sola determina ción, se debe hallar el promedio y entonces propagar el err or en
cada determinación. Se repor ta la infor mación con las cifras significativas correctas y el promedio del
error propagado.
V.
Propagación de errores experimentales
Para cantidades físicas medidas indirectamente que se obtienen calculándolas de medidas obtenidas
directamente.
Utilizamos el promedio aritmético de cada medida experimental para calcular el resultado final y no
calculamos el resultado que corresponde a cada medida experimental y luego buscamos el promedio.
A. Incertidumbre o error en el resultado final
--dependerá de la precisión y exactitud de las medidas experimentales afectando o propagándose en
el resultado del valor calculado
B. Ejemplo sencillo:
A = B r2
© 1997 - 2000 I. Nieves Martínez
Página - 5 -
TRATAMIENTO ESTADÍSTICO
Si el valor de r puede estar entre ro + * r y r o - * r , entonces el área calculada estará entre Ao + *A
y Ao - * A utilizando A = B r3 para calcular * A
Ao + * A = B (ro + * r)2 = B ro 2 + 2 B ro * r + B (* r)2
Como (* r)2 es un número pequeño60 (descartable) y B ro 2 = Ao
Ao ± * A = Ao ± 2 B ro * r, entonces * A = 2 B ro * r. Noten que
en ro .
evaluado
Por lo tanto, * A = error en A expresado por:
o en términos relativos
C. Caso General: Si la medida experimental es función de (x, y, z), entonces el error en
está dado por dF de acuerdo a:
F (x, y, z)
o en términos de la variación de la cantidad calculada
Incertidumbre en F
donde ) x, ) y, ) z son índices de precisión: desviación, estándar, promedio o incertidumbre del
instrumento.
son las derivadas parciales de la ecuación que
relaciona las variables.
Para resolver los problemas de signo se definen:
1)
Error máximo propagado
* Fmax prop = () F)max prop = ) F1 + ) F2 + ) F3 que dependen de la variable x, y y z.
2)
Error más probable propagado (“Root Mean Square”)
© 1997 - 2000 I. Nieves Martínez
Página - 6 -
TRATAMIENTO ESTADÍSTICO
Observaciones:
1) Si una de las medidas experimentales está sujeta a una incertidumbre relativa mucho mayor que el
de las otras medidas, esta medida determinará la incertidumbre del resultado final.
2) El cálculo no incluye errores sistemáticos.
EJEMPLO: TERMOMETRIA DE GASES
Utilizando la Ley de Gases Ideales y medidas de PV para determinar T, (PV = nRT)
Experimentalmente se mide P, V y n
P = 50.0 torr
V = 1000.0 cm3
n = 0.050 moles
R = 62.4 x 103 cm3 torr mol --1 K--1
)P = 0.1 torr
)V = 0.1 cm3
)n = ± 0.001 mol
Entonces: T = f (P, V, n) R
Noten que:
;
;
El error absoluto es:
Determinando las derivadas correspondientes resulta en la expresión:
o en términos del error relativo
Al sustituir los valores de ) V,) P y ) n se obtiene un ) T . 0.2 K
© 1997 - 2000 I. Nieves Martínez
Página - 7 -
TRATAMIENTO ESTADÍSTICO
VI. Método para ajustar los datos experimentales a una ecuación: Método del cuadrado mínimo.
(“Least Square”)
A. Si y = mx + b y experimentalmente obtenemos:
Esto no quiere decir que los dos (2) valores no están relacionados linealmente. Queremos encontrar
la mejor ecuación lineal entre x1 y y1 , por lo ta nto:
1)
Queremos determinar el valor de m y b que mejor represente las observaciones experimentales.
2)
Además, vamos a asumir que la mejor línea recta que se ajusta a los puntos experimentales es
aquella para la cual la suma de los cuadrados de las desviaciones entre el valor medido
experimentalmente y el que predice la mejor línea es un mínimo. Cierto para la distribución de
errores que obedece la distribución Gaussiana.
3)
Consideraremos solamente desviaciones en la variable dependiente; generalmente estas son
mayores que en la variable independiente.
La desviación de los puntos experimentales bajo o sobre la mejor línea está dada para un punto i de
los datos experimentales como:
* yi
=
desviación
yi
valor teoría
mejor línea
-
yi
expt.
=
(mxi + b) - yi
expt.
De acuerdo con el principio cuadrado mínimo, la mejor línea recta se obtiene cuando la suma de los
cuadra dos de las desviaciones es un mínimo. Ajustamos valores de m y b hasta que esta condición
se cumpla.
N es el # total de medidas
expandiendo
© 1997 - 2000 I. Nieves Martínez
Página - 8 -
TRATAMIENTO ESTADÍSTICO
condición para que S sea un mínimo:
Rearreglando:
Resolviendo ecuaciones simultáneas
© 1997 - 2000 I. Nieves Martínez
Página - 9 -
TRATAMIENTO ESTADÍSTICO
Resolviendo los determinantes:
Para facilitar el trabajo E xi , E yi, etc. se pueden tabular.
B. Error en la pendiente y el intercepto:
Haciendo análisis del error más probable propagado en m y b se obtiene:
donde
© 1997 - 2000 I. Nieves Martínez
y * yi = yi (exp) - yi (mejor linea)
Página - 10 -