Document

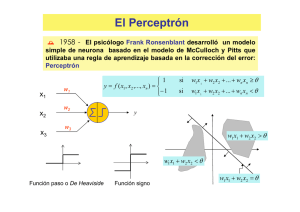
El Perceptrón
´ 1958 - El psicólogo Frank Ronsenblant desarrolló un modelo
simple de neurona basado en el modelo de McCulloch y Pitts que
utilizaba una regla de aprendizaje basada en la corrección del error:
Perceptrón
x1
x2
x3
w1
w2
 1
y = f ( x1 , x2 ,..., xn ) = 
− 1
si
w1 x1 + w2 x2 + ... + wn xn ≥ θ
si
w1 x 1 + w2 x2 + ... + wn xn < θ
y
w3
w1 x1 + w2 x2 > θ
w1 x1 + w2 x2 < θ
Función paso o De Heaviside
Función signo
w1 x1 + w2 x2 = θ
¿Qué se pretende con el Perceptrón?
Se dispone de la siguiente información:
L Conjunto de patrones {xk}, k = 1,2,…,p1 , de la clase C1
(zk = 1)
L Conjunto de patrones {xr}, k = p1+1,...,p , de la clase C2
(zr = -1)
Se pretende que el perceptrón asigne a cada entrada (patrón xk) la
siguiendo un proceso de corrección de error
salida deseada zk
(aprendizaje) para determinar los pesos sinápticos apropiados
Regla de aprendizaje del Perceptrón:
w j (k ) + 2ηx j (k )

w j (k + 1) = w j (k )

w j (k ) − 2ηx j (k )
∆w j (k ) = η (k )[z (k ) − y (k )]x j (k )
si y (k ) = −1 y z (k ) = 1,
si y (k ) = z (k )
si y (k ) = 1 y z (k ) = −1
error
tasa de
aprendizaje
¿Cómo se modifica el sesgo θ ?
w1 x1 + w2 x2 + ... + wn xn ≥ θ
x1
x2
x3
−1
⇔ w1 x1 + w2 x2 + ... + wn xn + wn+1 xn+1 ≥ 0
w1
w2
θ
y
w1 x1 + w2 x2 + ... + wn xn + θ (−1) ≥ 0
w3
θ
−1
∆θ (k ) = −η (k )[z (k ) − y (k )]
Algoritmo del Perceptrón
Paso 0: Inicialización
Inicializar los pesos sinápticos con números aleatorios del intervalo [-1,1].
Ir al paso 1 con k=1
Paso 1: (k-ésima iteración)
 n+1

Calcular
y(k ) = sgn ∑ w j x j (k ) 
 j =1

Paso 2: Corrección de los pesos sinápticos
Si z(k) ≠ y(k) modificar los pesos sinápticos según la expresión:
w j (k + 1) = w j (k ) + η [z i (k ) − y i (k )]x j (k ) ,
j = 1,2,..., n + 1
Paso 3: Parada
Si no se han modificado los pesos en las últimas p iteraciones, es decir,
w j (r ) = w j (k ), j = 1,2,..., n + 1, r = k + 1,..., k + p
parar. La red se ha estabilizado.
En otro caso, ir al Paso 1 con k=k+1.
Teorema de convergencia del Perceptrón
Si el conjunto de patrones de entrenamiento con sus salidas deseadas,
{x1 ,z1}, {x2 ,z2},…,{ xp ,zp},
es linealmente separable entonces el Perceptrón simple encuentra una
solución en un número finito de iteraciones
Demostración
Como es linealmente separable entonces existen
n
∑w x
> wn +1
si son de la clase C1
*
w
∑ j x j < wn+1
si son de la clase C2
j =1
n
j =1
*
j
j
w1* , w2* ,..., wn*+1
θ
Demostración
∑ (w (k + 1) − w ) = ∑ (w (k ) + η[z (k ) − y(k )]x (k ) − w )
n +1
j
j =1
n +1
* 2
j
(
= ∑ w j (k ) − w
j =1
)
* 2
j
n +1
j
j =1
* 2
j
j
+ η [z (k ) − y (k )]
2
2
n +1
∑ x (k )
j =1
2
j
n +1
(
)
+ 2η [z (k ) − y (k )]∑ w j (k ) − w*j x j (k )
j =1
n +1
n +1
j =1
j =1
+ 2η [z (k ) − y (k )](∑ w j (k ) x j (k )) −2η [z (k ) − y (k )]∑ w*j x j (k )
n +1
− 2 ∑ w j (k )x j (k )
j =1
n +1
(
≤ ∑ w j (k ) − w
j =1
)
* 2
j
+ 4η
2
n +1
∑ x (k )
j =1
2
j
n +1
+ 0 − 4η ∑ w*j x j (k )
j =1
n +1
2 ∑ w*j x j (k )
j =1
Demostración
∑ (w (k + 1) − w ) ≤ ∑ (w (k ) − w )
+ 4η
∑ (w (k + 1) − w ) ≤ ∑ (w (k ) − w )
+ 4η 2 L − 4ηT
n +1
* 2
j
j
j =1
n +1
* 2
j
j
j =1
n +1
j =1
* 2
j
j
n +1
j =1
* 2
j
j
2
n +1
∑ x (k )
j =1
2
j
n +1
− 4η ∑ w*j x j (k )
j =1
 n+1 *

T = min ∑ w j x j (k )
1≤ k ≤ p
 j =1

 n+1
2
L = max ∑ x j (k ) 
1≤ k ≤ p
 j =1

∑ (w (k + 1) − w ) ≤ ∑ (w (k ) − w )
n +1
j =1
Si
* 2
j
j
ηL − T < 0
n +1
j =1
j
* 2
j
+ 4η (ηL − T )
∑ (w (k + 1) − w ) < ∑ (w (k ) − w )
n +1
j =1
η<
T
L
j
* 2
j
n +1
j =1
j
* 2
j
Tasa de aprendizaje óptima
Se trata de elegir de la tasa de aprendizaje η manera que se
produzca un mayor decrecimiento del error en cada iteración
Error cuadrático en la iteración k+1
E (η ) = D(k + 1) = D(k ) + 4η
2
n +1
j =1
n +1
(
D(k + 1) = ∑ w j (k + 1) − w*j
n +1
n +1
j =1
j =1
*
(
)
(
)
(
)
x
k
−
4
η
w
k
x
k
−
4
η
w
∑ j
∑ j j
∑ j x j (k )
2
)
2
j =1
n +1
n +1
n +1
∂E (η )
2
= 8η ∑ x j (k ) − 4 ∑ w j (k )x j (k ) − 4 ∑ w*j x j (k ) = 0
∂η
j =1
j =1
j =1
n +1
η opt =
∑ w j (k )x j (k ) +
j =1
n +1
n +1
*
w
∑ j x j (k )
j =1
2∑ x j (k )
j =1
2
Tasa de aprendizaje óptima
n +1
η opt =
n +1
n +1
∑ w (k )x (k ) + ∑ w x (k )
j =1
j
j
n +1
j =1
*
j
j
η~opt =
2∑ x j (k )
2
∑ w (k )x (k )
j
j =1
n +1
∑ x j (k )
j =1
j =1
n +1
n +1
j =1
j =1
− 2 ∑ w j (k ) x j (k ) = [z (k ) − y (k )]∑ w j (k ) x j (k )
n +1
η~opt =
− [z (k ) − y (k )]∑ w j (k )x j (k )
j =1
n +1
2∑ x j (k )
j =1
j
2
2
Regla de aprendizaje normalizada
n +1
w j (k + 1) = w j (k ) −
[z (k ) − y (k )]∑ w j (k )x j (k )
j =1
n +1
2∑ x j (k )
2
j =1
n +1
w j (k + 1) = w j (k ) − 2
∑ w (k )x (k )
j =1
n +1
j
j
∑ x j (k )
j =1
2
x j (k )
[z (k ) − y(k )]x j (k )
Regla de aprendizaje normalizada
n +1
w (k + 1) = ∑ w j (k + 1) 2
2
j =1
2
n +1
 n +1

w j (k ) x j (k ) n +1
 ∑ w j (k ) x j (k ) 
∑
n +1
n +1
j =1
 − 4 j =1
= ∑ w j (k ) 2 + ∑ x j (k ) 2  2 n +1
w j (k ) x j (k )
∑
n +1


j =1
j =1
x j (k ) 2 
x j (k ) 2 i =1

∑
∑
j =1
j =1


n +1
= ∑ w j (k ) 2 = 1
j =1
Interpretación de la regla de aprendizaje del
Perceptrón
n +1
w x = ∑ wj x j ≥ 0
T
j =1
n +1
w x = ∑ wj x j < 0
T
∀x ∈ C1
∀x ∈ C2
j =1
y = sgn(w T x) = z , ∀x ∈ C1 ∪ C 2
Interpretación de la regla de aprendizaje del Perceptrón
Se realizan las correcciones siempre y cuando se producen clasificaciones
incorrectas.
Z= +1
Y= -1
El aprendizaje debe
acercar los vectores W y X
W(k+1)= W(k) + α * X
Interpretación de la regla de aprendizaje del Perceptrón
Se realizan las correcciones siempre y cuando se producen clasificaciones
incorrectas.
z= -1
y= +1
El aprendizaje debe
alejar los vectores w y x
W(k+1)= W(k) - α * X
Interpretación de la regla de aprendizaje del Perceptrón
a)
b)
w(k+1)= w(k) + α * x j
w(k+1)= w(k) - α * x j
z= +1 y= -1
z= -1 y= +1
w j (k + 1) = w j (k ) + η [z i (k ) − y i (k )]x j (k ) ,
η = α/2
j = 1,2,..., n + 1
Ejemplo
☺ Diseña un perceptrón que implemente la función
lógica AND
AND
Entradas
(1, 1)
x1
Salidas
1
(1, −1)
−1
x2
(−1, 1)
−1
−1
(−1,−1)
−1
Paso 0: Inicialización aleatoria
w1 = 0.4,
w2 = − 0.2,
θ = 0.6,
w1
w2
θ
y
Diseña un perceptrón que implemente la función
lógica AND
☺
1
−1
−1
0.3
−0.2
y
−0.6
Paso 1:
Patrón de entrada (1,−1):
h = 0.3(1) − 0.2(−1) − 0.6(−1) = 1.1
Paso 2: Corrección de los pesos sinápticos
w1 (1) = w1 (0) − 2η1 = 0.3 − 1 = −0.7
w2 (1) = w2 (0) − 2η (−1) = −0.2 + 1 = 0.8
θ (1) = θ (0) − 2η (−1) = −0.6 + 1 = 0.4
y=1
Elegimos η=0.5
Diseña un perceptrón que implemente la función
lógica AND
☺
−1
−1
−1
−0.7
0.8
y
0.4
Paso 1:
Patrón de entrada (−1,−1):
h = −0.7(−1) + 0.8(−1) + 0.4(−1) = −0.5
Como y = − 1 y z = −1 la clasificación es correcta
y=−1
Diseña un perceptrón que implemente la función
lógica AND
☺
1
1
−1
−0.7
0.8
y
0.4
Paso 1:
Patrón de entrada (1,1):
h = −0.7(1) + 0.8(1) + 0.4(−1) = −0.3
Paso 2: Corrección de los pesos sinápticos
w1 (2) = w1 (1) + 2η (1) = −0.7 + 1 = 0.3
w2 (2) = w2 (1) + 2η (1) = 0.8 + 1 = 1.8
θ (2) = θ (1) + 2η (−1) = 0.4 − 1 = −0.6
Elegimos η = 0.5
y=−1
Diseña un perceptrón que implemente la función
lógica AND
☺
−1
1
−1
0.3
1.8
y
−0.6
Paso 1:
Patrón de entrada (−1,1):
h = 0.3(−1) + 1.8(1) − 0.6(−1) = 2.1
Paso 2: Corrección de los pesos sinápticos
w1 (3) = w1 (2) − 2η (−1) = 0.3 + 1 = 1.3
w2 (3) = w2 (2) − 2η (1) = 1.8 − 1 = 0.8
θ (3) = θ (2) − 2η (−1) = −0.6 + 1 = 0.4
y=1
Elegimos η = 0.5
Diseña un perceptrón que implemente la función
lógica AND
☺
-1
1
−1
1.3
0.8
y
0.4
Patrón (1,1):
h = 1.3(1) + 0.8(1) + 0.4(−1) = 2.7
Patrón (1,−1):
h = 1.3(1) + 0.8(−1) + 0.4(−1) = 0.1
Patrón (−1,−1): h = 1.3(−1) + 0.8( −1) + 0.4(−1) = −2.5
Patrón (−1,1):
h = 1.3(−1) + 0.8(1) + 0.4(−1) = −0.9
1.3x1 + 0.8 x2 − 0.4 = 0
Diseña un perceptrón que implemente la función
lógica AND
☺
1
−1
−1
1.3
0.8
y
0.4
Paso 1:
Patrón de entrada (1,−1):
h = 1.3(1) + 0.8(−1) + 0.4(−1) = 0.1
Paso 2: Corrección de los pesos sinápticos
w1 (3) = w1 (2) − 2η (1) = 1.3 − 1 = 0.7
w2 (3) = w2 (2) − 2η (−1) = 0.8 + 1 = 1.8
θ (3) = θ (2) − 2η (−1) = 0.4 + 1 = 1.4
y=1
Elegimos η = 0.5
Diseña un perceptrón que implemente la función
lógica AND
☺
1
−1
−1
0.7
1.8
y
1.4
Paso 1:
Patrón de entrada (1,−1):
h = 1.3(1) + 0.8(−1) + 0.4(−1) = 0.1
Paso 2: Corrección de los pesos sinápticos
w1 (3) = w1 (2) − 2η (1) = 1.3 − 1 = 0.7
w2 (3) = w2 (2) − 2η (−1) = 0.8 + 1 = 1.8
θ (3) = θ (2) − 2η (−1) = 0.4 + 1 = 1.4
y=1
Elegimos η = 0.5
Algoritmo de aprendizaje por lotes
del Perceptrón: Evaluamos las salidas de la red para todos los
patrones de entrenamiento y recién modificamos los pesos
Paso 0: Inicialización
Inicializar los pesos sinápticos con números aleatorios del
intervalo [-1,1]. Fijar un valor de parada s. Ir al paso 1 con k=1
Paso 1: (k-ésima iteración) Corrección de los pesos sinápticos
w ( k + 1) = w ( k ) + η ( k )
∑ a( k )
k∈I ( w )
Paso 2: Parada
Si
η (k )
∑ a( k ) < s
 x(k) si z(k) =1
a(k)=
−x(k) si z(k) =−1
parar.
k∈I ( w )
En otro caso, ir al Paso 1 con k=k+1.
Tipos de aprendizaje
Algoritmo de aprendizaje continuo (on-line)
Evaluamos las salidas de la red para el patrón presentado y
modificamos los pesos sinápticos de acuerdo a ese ejemplo
Algoritmo de aprendizaje por lotes (batch)
Evaluamos las salidas de la red para todos los patrones de
entrenamiento y recién modificamos los pesos