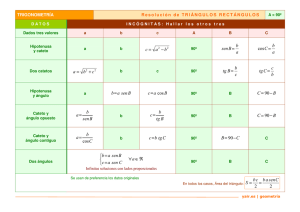
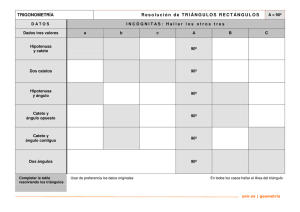
Triangulos rectangulos y funciones trigonomometricas.
Anuncio

FUNCIONES TRIGONOMÉTRICA DE UN TRIÁNGULO RECTÁNGULO. Las funciones trigonométricas de un triángulo rectángulo son las razones o relaciones entre sus lados. Razón. La razón de un número “a” con respecto a otro número “b” distinto de cero, es el cociente que resulta de dividir “a” entre “b”, esto es que la razón es el número que resulta de comparar por cociente dos magnitudes. a = Razón b Las razones que existen entre los lados de un triángulo rectángulo varían según el ángulo del que se trate, a estas razones se les conoce como funciones trigonométricas. Existen seis funciones trigonométricas las cuales son: Nombre de la función. Abreviatura. Seno. Sen Coseno. Cos Tangente. Tan Cotangente. Cot Secante. Sec Cosecante. Csc Si consideramos a un triángulo rectángulo cuyos ángulos son A, B y C y como las longitudes de los lados opuestos a dichos ángulos a, b, y c, La hipotenusa se designa como c y al ángulo recto como C. B c a C b Para el ángulo ∠ A. Para el ángulo ∠ B c es la hipotenusa, a es el cateto opuesto y b es el cateto adyacente. c es la hipotenusa, b es el cateto opuesto y a es el cateto adyacente. A Las funciones trigonométricas se definen como: Seno = cateto opuesto c.o = hipotenusa h Coseno = cateto adyacente c.a = hipotenusa h Tangente = cateto opuesto c.o = cateto adyacente c.a Co tan gente = Secante = cateto adyacente c.a = cateto opuesto c.o hipotenusa h = cateto adyacente c.a Co sec ante = hipotenusa h = cateto opuesto c.o Para el caso del siguiente triángulo rectángulo las funciones trigonométricas quedarían como: B c a C b A Para el ángulo A. Para el ángulo B. SenA = c.o h por lo tanto SenA = a c SenB = c.o h por lo tanto SenB = b c CosA = c.a h por lo tanto CosA = b c CosB = c.a h por lo tanto CosB = a c TanA = c.o c.a por lo tanto TanA = a b TanB = c.o c.a por lo tanto TanB = b a CotA = c.a c.o Por lo tanto CotA = b a CotB = c.a c.o Por lo tanto CotB = a b SecA = h c.a Por lo tanto SecA = c b SecB = h c.a Por lo tanto SecB = c a CscA = h c.o Por lo tanto CscA = c a CscB = h c.o Por lo tanto CscB = c b FUNCIONES TRIGONOMÉTRICAS RECÍPROCAS. Fracciones recíprocas. Dos funciones son recíprocas cuando una resulta de invertir los términos de la otra, así como el producto de estas dos funciones es igual a la unidad. Ejemplos. 1 2 es recíproco de y su producto 2 1 1 2 2 = = 1 2 1 2 3 8 es recíproco de y su producto 8 3 3 8 24 =1 = 8 3 24 Las funciones trigonométricas recíprocas son aquellas cuyo producto es la unidad, si consideramos al ángulo A del triángulo de la siguiente figura tendríamos lo siguiente: B c a C SenA = a c CosA = b c TanA = a b CotA = b a SecA = c b CscA = c a b A Funciones recíprocas. Como las siguientes funciones son recíprocas se tienen las siguientes identidades entre ellas. (Sen A)(Csc A) = 1 (Cos A)(Sec A) = 1 (Tan A)(Cot A) = 1 SenA = 1 CscA CosA = 1 SecA TanA = 1 CotA CscA = 1 SenA SecA = 1 CosA CotA = 1 TanA RESOLUCIÓN DE TRIÁNGULOS RECTÁNGULOS. En este tema resolveremos triángulos rectángulos aplicando los conceptos de la trigonometría y el Teorema de Pitágoras. En un triángulo hay seis elementos: tres lados a los que llamaremos a, b y c, tres ángulos a los que llamaremos A, B y C, donde el ángulo C es un ángulo recto, tal como se muestra en la siguiente figura. B La expresión matemática que representa el teorema de Pitágoras es c2= a2 + b2 c Donde catetos. a c es la hipotenusa, a y b son los A C b Existen cuatro casos diferentes en la resolución de estos triángulos, los cuales son: 1. 2. 3. 4. Que se conozca la hipotenusa y un ángulo agudo. Que se conozca un cateto y un ángulo agudo. Que se conozca la hipotenusa y un cateto. Que se conozcan dos catetos. Ejemplos resueltos de triángulos rectángulos. Caso 1. Resolver el siguiente triángulo Rectángulo. B Por definición. CosA = 30º Cos30º = a C c.a h c =9 A b Solución. ∠ A + ∠ B= 90º por ser complementarios. ∠ B = 90º - ∠ A ∠ B = 90º - 30º ∠ B = 60º b 9 b = (9)(Cos 30 º ) Por el Pitágoras teorema de c2= a2 + b2 a = c 2 −b 2 a = 9 2 − 7.79 2 b = (9)(0.8660 ) a = 81 − 60.68 b = 7.794 a = 20.31 a = 4.5 Por el teorema de Por definición. Caso 2. Resolver el siguiente triángulo c.a CosB = rectángulo. h B 10 Cos 40º = c 40º c 10 c= a= 10 Cos 40º 10 c= 0.7660 A C b Solución. ∠ A + ∠ B= 90º por ser complementarios ∠ A = 90º - ∠ B ∠ A = 90º - 40º ∠ A = 50º Caso 3. Resolver el siguiente triángulo rectángulo. B c =12 a A C b= 8 Caso 4. Resolver el siguiente triángulo rectángulo. B a=4 C A b =5 c= a= a= a= a= a 2 +b 2 c 2 −b 2 2 2 12 −8 144 − 64 c2= a2 + b2 b = c 2 −a 2 b = 13.05 2 − 10 2 b = 170.30 − 100 b = 70.30 c = 13.05 Solución. Por el teorema de Pitágoras. Pitágoras. b = 8.39 c.a h 8 CosA = 12 CosA = 0.66 CosA = A=Cos-1(0.66) A=48.18° ∠ A + ∠ B= 90º Por ser complementarios. ∠ B = 90º - ∠ A ∠ B = 90º - 48.18º ∠ B = 41.82º 80 a= 8.94 Solución. Por definición. Por el teorema de c.o Pitágoras. TanA = c.a 2 2 4 c = a +b TanA = 5 c = 4 2 +5 2 TanA = 0.8 c = 16 + 25 A=Tan -1(0.8) A=38.5º c = 41 Por ser complementarios c = 6.40 ∠ B = 51.5º ∠ A + ∠ B= 90º ∠ B = 90º - ∠ A ∠ B = 90º - 38.5º 5. Calcular el ángulo de elevación del sol en el momento en que un árbol de 4m de alto proyecta una sombra de 7.5m. Solución. 4m ∠A A Sombra = 7.5m Por definición. c.o TanA = c.a TanA = 4m 7. 5m TanA = 0.53 A=Tan -1(0.53) A=28º 6. ¿Qué altura alcanza sobre un muro una escalera de 8m de largo, si la escalera forma un ángulo de 60º con el piso? Solución. 8m Altura Sen60º = c.o h Sen60 º = Altura 8m Altura = (8m)( Sen 60º ) 60º Altura = (8m)(0.8660) Altura = 6.928