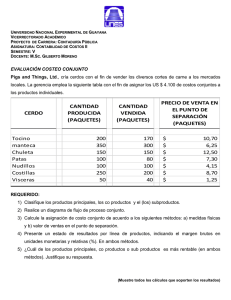
Manejo de la información

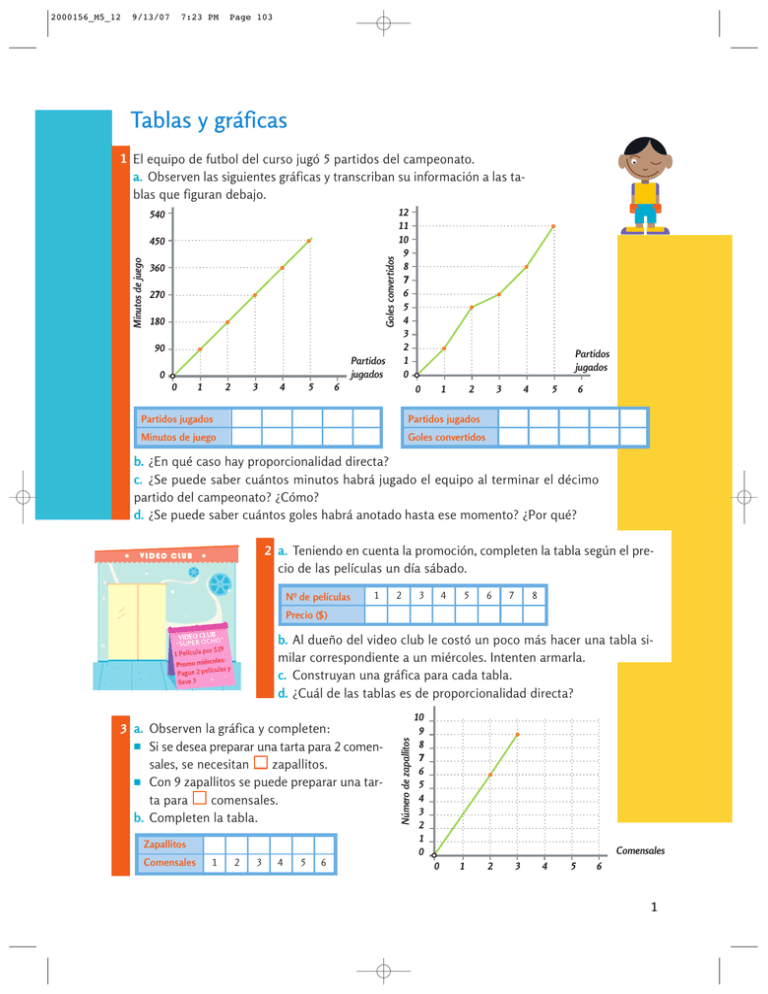
2000156_M5_12
9/13/07
7:23 PM
Page 103
Tablas y gráficas
1 El equipo de futbol del curso jugó 5 partidos del campeonato.
a. Observen las siguientes gráficas y transcriban su información a las tablas que figuran debajo.
540
Goles convertidos
Minutos de juego
450
360
270
180
90
Partidos
jugados
0
0
1
2
3
4
5
12
11
10
9
8
7
6
5
4
3
2
1
0
6
Partidos
jugados
0
1
2
Partidos jugados
Partidos jugados
Minutos de juego
Goles convertidos
3
4
5
6
b. ¿En qué caso hay proporcionalidad directa?
c. ¿Se puede saber cuántos minutos habrá jugado el equipo al terminar el décimo
partido del campeonato? ¿Cómo?
d. ¿Se puede saber cuántos goles habrá anotado hasta ese momento? ¿Por qué?
2 a. Teniendo en cuenta la promoción, completen la tabla según el precio de las películas un día sábado.
Nº de películas
1
2
3
4
5
6
7
8
Precio ($)
3 a. Observen la gráfica y completen:
Si se desea preparar una tarta para 2 comensales, se necesitan
zapallitos.
Con 9 zapallitos se puede preparar una tarta para
comensales.
b. Completen la tabla.
Zapallitos
Comensales
1
2
3
4
5
6
Número de zapallitos
b. Al dueño del video club le costó un poco más hacer una tabla similar correspondiente a un miércoles. Intenten armarla.
c. Construyan una gráfica para cada tabla.
d. ¿Cuál de las tablas es de proporcionalidad directa?
10
9
8
7
6
5
4
3
2
1
0
Comensales
0
1
2
3
4
5
6
1
2000156_M5_12
9/13/07
7:23 PM
Page 104
Cálculo de cantidades proporcionales
4 Actividad resuelta
Con la canilla de un patio se puede llenar un bidón de 3 litros en 54 segundos. ¿Cuánto tiempo se necesita para llenar un bidón de 7 litros con la misma canilla? Resuelvan
el problema por reducción a la unidad y por regla de tres.
÷3
Solución:
a. Reducción a la unidad. Construimos una tabla y dividimos
Capacidad (l)
3
por 3 para averiguar en cuántos segundos la canilla llena 1 liTiempo (s)
54
tro. Luego multiplicamos por 7 para averiguar en cuántos segundos llena un bidón de 7 litros: (54 ÷ 3) x 7 = 126.
÷3
b. Regla de tres. Planteamos:
3 litros
54 segundos
7 litros
x
Resolvemos: (7 x 54) ÷ 3 = 126. Para llenar un bidón de 7 litros, serán necesarios 126
segundos.
5 Las familias Pérez y López fueron al teatro a
ver La vuelta manzana. El precio de las entradas era el mismo para niños que para adultos.
¿Cuánto le saldrán las entradas a la familia
Pérez?
Reservé
3 entradas a nombre
de López.
7 Si 200 cm de soga cuestan $3.40, ¿cuánto costarán 700 cm de la misma soga?
8 Completen las siguientes tablas, en las que se sabe que hay proporcionalidad directa.
a.
b.
5
7.5
2
7
9
11
3
5
7
105
9
11
1
7
18
126
x7
Aquí tiene.
Son $26.25.
6 Soledad compró 2 m de soga para saltar, por $3.40.
a. A sus amigos les gusta saltar a la soga de a muchos. Para eso, compraron 7 m.
¿Cuánto les costaron?
b. ¿Cuántos metros de la misma soga se pueden comprar con $8.50?
3
x7
2000156_M5_12
9/13/07
7:23 PM
Page 105
2 paquetes de fideos por $4.30
3 paquetes de fideos por $5.70
9 En el supermercado Sudoeste, doña Tota y doña Cata encontraron estos precios:
Cada una quería 4 paquetes de fideos, pero calcularon distinto.
2 paquetes de fideos ...... $4.30
4 paquetes de fideos ...... x
x = (4 x 4.30) ÷ 2 = 8.60
Los fideos saldrán $8.60.
3 paquetes de fideos ......... $5.70
4 paquetes de fideos ......... x
x = (4 x 5.70) ÷ 3 = 7.60
Los fideos saldrán $7.60.
a. ¿Alguna de las dos tiene razón? ¿Por qué?
b. ¿Qué dato falta para saber realmente cuánto costarán 4 paquetes?
Número de galletas
Peso de las galletas (sin caja)
6
10
15
18
22
630
540
450
Peso (gramos)
10 En una fábrica envasan cajas de dos docenas
de galletas. La gráfica muestra cómo va variando el peso de la caja, según el número de
galletas que se le van agregando.
a. ¿Cuánto pesa la caja vacía?
b. Completen la tabla.
360
270
180
90
30
0
0
6
12
Galletas
18
24
11 Cuando dos cantidades son directamente proporcionales, al dividir cada
número por el que le corresponde en la tabla se obtiene siempre el mismo resultado.
Revisen, por ejemplo, la tabla 3 del comienzo de este tema.
a. Verifiquen con la calculadora:
1 ÷ 1.5 = 0.666...
2 ÷ 3 = 0.666...
3 ÷ 4.5 = 0.666...
5 ÷ 7.5 = 0.666..., etcétera.
También, si dividen “al revés”, se obtiene siempre un mismo resultado:
1.5 ÷ 1 = 1.5
3 ÷ 2 = 1.5
4.5 ÷ 3 = 1.5
7.5 ÷ 5 = 1.5, etcétera.
b. Comprueben con la calculadora que esto ocurre con todas las tablas de
proporcionalidad directa que aparecieron en este tema.
c. Verifiquen con la calculadora que la propiedad no se cumple en ninguna de las tablas que no son de proporcionalidad directa.
3
2000156_M5_12
9/13/07
7:23 PM
Page 107
Actividades integradoras
15 En una casa de fotografía, el revelado de un rollo de 24 fotos en ta-
maño 10 cm x 15 cm, más un álbum para las fotos, cuesta en total
$19.10. El álbum suelto cuesta $2.30. La casa no hace ningún tipo de
descuento por cantidad. ¿Cuánto costará revelar 36 fotos del mismo tamaño, sin el álbum?
16 Este plano muestra el lugar del bosque, junto al lago, donde uno de los tres cochinitos construyó su casa de ladrillos. En el plano, 0.5 cm corresponden a una medida real de 15 metros. El cochinito les dijo a sus dos hermanos que construyeran
sus casas a no más de 50 metros de la de él. De esta manera, si el lobo los perseguía, podrían refugiarse a tiempo en la edificación más sólida.
Determinen en qué zona del plano pueden construir sus casas los otros cochinitos.
(Tengan en cuenta que no pueden hacerlo en el lago.)
17 La principal unidad de longitud que utilizamos es el
metro (m). Pero en otros países se usan otras unidades.
Por ejemplo, 1 pulgada equivale a 0.0254 m (o 2.54 cm); 1 pie equivale a 0.305 m aproximadamente, y 1 yarda equivale a alrededor de
© ediciones sm S.A. Prohibida su fotocopia. Ley 11.723
0.914 m.
a. Calculen cuál es su estatura, medida en pies y en yardas.
b. Calculen y completen:
1 pie equivale a
yardas.
20 pulgadas equivalen a
1 yarda equivale a
centímetros.
pies.
4
2000156_M5_12
9/13/07
7:23 PM
Page 108
Para hacer con mate
Elaborar gráficas con la computadora
La computadora puede ser de gran ayuda para construir gráficas a
partir de tablas de datos. Todas las gráficas que aparecen en este libro
fueron realizadas con una computadora.
Seguramente, las computadoras de la escuela tienen una hoja de
cálculo (Excel). Este programa puede usarse de forma muy sencilla para
hacer gráficas como las de este tema. Podrán construir una siguiendo
estas instrucciones:
Paso 1. Abran el programa. Verán en el monitor una cuadrícula como la que se muestra en la figura. Cada rectán-
Botellas
1
Litros de gaseosa 1,5
2
3
3
5
4,5 7,5
gulo de la cuadrícula se llama celda.
Paso 2. Elijan una tabla de datos para graficar.
Hagan clic sobre la primera celda de arriba a la izquierda
(esa celda se llama A1, ¿se dan cuenta por qué?). Ingresen el primer valor de la tabla.
Paso 3. Ingresen los demás valores de la tabla.
Paso 4. Para seleccionar todos los valores de la tabla,
hagan clic sobre la celda A1 y, sin soltar el botón del
mouse, arrastren la cruz hasta la última celda de la
derecha de la tabla.
Paso 5. En el menú Insertar, seleccionen la opción gráfico. Se abrirá una
ventana como la de la derecha.
Paso 6. En esta ventana, se ofrece gran variedad de tipos de gráficas
distintas. Las que nos interesan son las que se llaman XY (Dispersión).
Seleccionen esa opción.
Paso 7. A la derecha de la ventana, aparecerán distintas opciones para la gráfica. La más conveniente es la que
muestra los puntos unidos por una línea que permite
ver si están en una misma recta. Seleccionen ese ícono.
Paso 8. Hagan clic con el mouse en la opción Siguiente hasta finalizar la construcción de la gráfica.
Para practicar, construyan con Excel las gráficas de las distintas tablas de datos que aparecen en los problemas. Cuando vayan conociendo el programa,
descubrirán distintas opciones que sirven para modificar la gráfica.
5
10
15