Capítulo 27 - Papel de la estadística

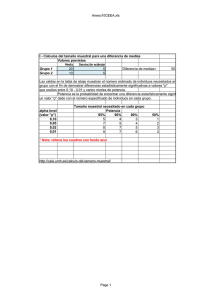
Capítulo
| 27 |
Papel de la estadística
La estadística no es útil exclusivamente para el análi­
sis de los resultados, sino que debe considerarse una
parte integrante del método científico que se aplica
en diferentes fases de una investigación para facilitar
que se alcance el objetivo deseado (cuadro 27.1). En
la fase de análisis permite evaluar y cuantificar la
variabilidad debida al azar. La premisa previa para su
uso es que el estudio haya sido diseñado y ejecutado
de forma correcta.
Clásicamente, la estadística se diferencia en des­
criptiva e inferencial. La estadística descriptiva permite
organizar, presentar y sintetizar la información y es
fundamental en la revisión de los datos recogidos
en un estudio para asegurar su calidad y la validez
del análisis posterior, así como para describir las
características de los sujetos estudiados. La estadística
inferencial permite establecer conclusiones referidas a
poblaciones a partir de los resultados obtenidos en
muestras. Su aplicación en la fase de análisis tiene
dos finalidades principales: evaluar la variabilidad
aleatoria y controlar los factores de confusión.
Las técnicas de análisis estadístico pueden utili­
zarse para explorar conjuntos de datos sin hipótesis
previas o bien para confirmar hipótesis de trabajo.
Ambas finalidades están vinculadas a la naturaleza
de los objetivos del estudio, a la actitud con que el
investigador se enfrenta a los datos y a los términos
en que deberán interpretarse los resultados. Una
hipótesis solamente puede confirmarse mediante
un estudio diseñado con el propósito de hacerlo.
La exploración implica el rastreo de datos en busca
de información, sin objetivos concretos ni hipótesis
que hayan gobernado el diseño del estudio. La ex­
ploración puede servir para sugerir nuevas hipótesis,
pero de ningún modo para contrastarlas, sino que
la confirmación deberá obtenerse en un nuevo es­
tudio diseñado para ello. Ambas finalidades pueden
© 2013. Elsevier España, S.L. Reservados todos los derechos
coexistir en un estudio diseñado para confirmar una
hipótesis cuando se establecen objetivos secundarios
exploratorios. Aunque no están vinculadas a técnicas
de análisis concretas, las pruebas de contraste o de
significación estadística están dirigidas a confirmar
hipótesis, mientras que las técnicas exploratorias son
eminentemente gráficas y descriptivas. En este capítu­
lo se abordan, sobre todo, las bases de la utilización
de la inferencia estadística para confirmar la hipótesis de
trabajo y alcanzar el objetivo del estudio.
Variaciones del muestreo
En estadística, el término población se utiliza para
describir todas las posibles observaciones de una
determinada variable o todas las unidades sobre las
que podría haberse realizado una observación. El
significado preciso de este concepto varía en función
del contexto en que se utiliza. Puede tratarse de una
población de pacientes, de profesionales o de deter­
minaciones de laboratorio, e incluso difiere según
la localización geográfica y la fuente de sujetos u
observaciones utilizada. A menudo no tiene una
realidad física concreta, ya que, por ejemplo, la
población de pacientes con infección urinaria no
existe como tal, sino que el proceso va apareciendo
y desapareciendo en diferentes sujetos en función
de múltiples y variados factores.
En sentido amplio, el término muestra se refiere a
cualquier conjunto específico de sujetos u observa­
ciones procedentes de una población determinada.
Para que sea útil y permita aplicar las técnicas es­
tadísticas, se requiere que la muestra tenga un ta­
maño razonable y sea representativa de la población
de la que procede. Un tamaño grande no asegura la
representatividad, sino que ésta radica básicamente
253
Parte
|4|
Interpretación de resultados
Cuadro 27.1 Fases de una investigación
en las que interviene
la estadística
• Selección de la variable de respuesta
• Definición de los criterios de selección
de la población de estudio
• Elección de la técnica de selección de los sujetos
• Cálculo del número de sujetos necesarios
• Selección de las variables que deben ser medidas
• Medición de las variables (precisión y exactitud)
• Descripción de la muestra de sujetos estudiados
• Estimación de la magnitud del efecto o respuesta
observada
• Comparación del efecto observado en diferentes
grupos
• Control de los factores de confusión
• Interpretación de los resultados
en que la muestra se haya escogido aleatoriamente
y esté libre de sesgos.
Se estudian muestras en lugar de poblaciones por
criterios de eficiencia. El propósito fundamental del
muestreo es estimar el valor de una determinada varia­
ble (parámetro) en la población, a partir de un núme­
ro menor de observaciones (muestra). Sin embargo,
tan sólo se estudia una de las múltiples muestras que
podrían seleccionarse de la población de referencia, en
cada una de las cuales podría obtenerse un valor dife­
rente, simplemente por azar. Las diferentes técnicas de
la estadística inferencial se fundamentan en que esta
variabilidad inherente al proceso de muestreo sigue
unas leyes conocidas y puede ser cuantificada.
Así, en el caso de una variable cuantitativa, en
cada muestra se obtendrá una media diferente. Si se
representa gráficamente la distribución de las medias
de todas las muestras posibles de un mismo tamaño,
se puede comprobar que sigue la ley normal. Esto
es cierto si la variable es normal en la población
de origen. Pero, aunque no lo sea, la distribución de
las medias muestrales tiende a ser normal a medida
que su tamaño aumenta, y se acepta que, si las mues­
tras son de más de 30 sujetos, la distribución de sus
medias es normal.
Esta distribución de medias muestrales tiene dos
características que la hacen especialmente interesante.
La primera es que su media es la media de la población
de la que proceden las muestras; es decir, las medias
muestrales se distribuyen normalmente alrededor de la
media poblacional desconocida que se quiere estimar.
La segunda es que la desviación estándar de dicha dis­
__
tribución tiene el valor σ/​√ n ,​  donde σ es la desviación
estándar de la población de origen y n el tamaño de
la muestra. Este valor es conocido como error estándar
254
de la media (EEM), y mide la dispersión de las medias
muestrales respecto de la media poblacional. No debe
confundirse con la desviación estándar, cuyos valores
miden la dispersión de los valores de la variable (no de
las medias muestrales) en los sujetos de la población
(σ) o de la muestra (DE,s), respectivamente (fig. 27.1).
Puede deducirse fácilmente que el EEM disminuye
cuando aumenta el tamaño de la muestra n, lo que
explica el hecho de que las muestras grandes estimen
el valor poblacional con mayor precisión.
En el caso de las variables cualitativas, la distribución
de la proporción sigue la ley binomial. Sin embargo,
cuando los productos n·p y n·(1 − p) son superiores a
5, la distribución se asemeja bastante a la normal. Así,
las proporciones observadas en las muestras se distribu­
yen alrededor de la verdadera proporción poblacional,
y la dispersión de esta distribución se mide mediante
el_________
error estándar de la proporción (EEP), cuyo valor es​
y tiene características similares al EEM.
√ p (1−p)/n ​, 
Estimación de un parámetro
poblacional: intervalo
de confianza
Un objetivo frecuente en la investigación médica
es estimar un parámetro poblacional a partir de los
valores que la variable de interés adopta en los indi­
viduos de una muestra. Si la variable es cuantitativa,
la media (m) y la desviación estándar (DE) obser­
vadas en la muestra son la mejor estimación dis­
ponible de los verdaderos valores de los parámetros
poblacionales. Pero ¿cuáles serían los resultados si
se repitiera el estudio en múltiples ocasiones?
Ejemplo 27.1. Supongamos que en una muestra de
60 sujetos se observa una media de presión arterial sis­
tólica (PAS) de 150 mmHg, con una DE de 20 mmHg,
y que se desea conocer el verdadero valor de la PAS
media en la población de referencia. En principio, el
valor más probable es la estimación puntual obtenida
en la muestra (150 mmHg), pero, dado que si se hu­
biera estudiado una muestra diferente probablemente
se habría obtenido un resultado distinto, se necesita
una medida de la precisión de esta estimación, lo
que se hace mediante el cálculo del llamado intervalo
de confianza (IC) (cuadro 27.2). Habitualmente se
trabaja con una confianza del 95%, es decir, con un
valor a del 5%, que corresponde a un valor Za de
1,96. Aplicando la fórmula, se obtendría un IC del
95%, que sería aproximadamente de 150 ± 5 mmHg,
lo que significa que hay un 95% de confianza de que
el valor medio de la PAS de la población de referencia
se encuentre entre 145 y 155 mmHg.
Papel de la estadística
Capítulo
| 27 |
© Elsevier. Fotocopiar sin autorización es un delito.
Figura 27.1 Diferencia entre desviación estándar y error estándar de la media.
De forma similar se calcularía el IC en el caso de
una variable cualitativa (ver cuadro 27.2).
El IC proporciona mucha más información que la
estimación puntual, ya que permite evaluar la precisión
con que se ha estimado el parámetro poblacional; es de­
cir, entre qué límites se tiene una determinada confian­
za de que esté situado su verdadero, pero desconocido,
valor. Si se repitiera el estudio en 100 ocasiones, el IC
incluiría el verdadero valor en 95 de ellas. Sin embargo,
no puede descartarse totalmente que el estudio corres­
ponda a una de las cinco ocasiones restantes.
De las fórmulas del cuadro 27.2 se deduce que
un aumento del número de sujetos conduce a un
IC más estrecho y a un aumento de la precisión de
la estimación. La amplitud del IC depende también
del grado de confianza que se utilice, y aumenta a
medida que se incrementa la confianza deseada.
En el cálculo del IC se asume que se ha estudiado
una muestra aleatoria y representativa de la población
de referencia. Al interpretarlo, hay que tener en cuenta
la posibilidad de la existencia de otras fuentes de error
no debidas al azar (errores sistemáticos o sesgos). Si
éstas existen, o si la muestra no es aleatoria, el error
de la estimación puede ser mayor que el sugerido por
la amplitud del intervalo.
Siempre que se realizan inferencias sobre paráme­
tros poblacionales a partir de criterios estadísticos
muestrales, los resultados deben expresarse como IC,
y no sólo como estimaciones puntuales, para poder
valorar la precisión de la estimación.
Contraste de hipótesis
Aunque la situación es similar a la anterior, dado que
se pretende descubrir algo sobre las poblaciones a
partir del estudio de muestras, las pruebas de con­
traste de hipótesis, o de significación ­estadística,
255
Parte
|4|
Interpretación de resultados
Cuadro 27.2 Cálculo del intervalo
de confianza (IC)
en la estimación
de un parámetro poblacional
IC de una media (variable cuantitativa)*:
x–± (Za⋅EEM)
s
___
siendo EEM = ​ ____
   ​ 
​√ n ​ 
IC de una proporción (variable cualitativa)**:
p ± (Za⋅EEP)
________
√
p⋅(1−p)
siendo EEP = ​ _______
​  n   
​ ​ 
 
x–: media observada en la muestra.
s: desviación estándar observada en la muestra.
n: número de individuos de la muestra.
EEM: error estándar de la media.
p: proporción observada en la muestra.
EEP: error estándar de la proporción.
Za: valor de la variable normal tipificada
correspondiente al valor a para un valor
de confianza (1 − a).
Este cálculo se basa en la distribución normal. El valor
de Za para un IC del 95% es 1,96. Para muestras de tamaño
inferior a 30 individuos, este valor debe sustituirse
por el de la distribución de la t de Student-Fisher para (n − 1)
grados de libertad.
*
Las variables cualitativas no presentan una distribución
normal. Las fórmulas de la tabla se basan en una
aproximación a la normalidad, aplicable cuando
los productos np y n·(1 − p) son mayores de 5. En caso
contrario, debe aplicarse una corrección al valor de Za.
**
valoran la variabilidad debida al azar de forma
diferente a la estimación de los parámetros.
Existen diversas pruebas estadísticas aplicables
en diferentes situaciones en función del número
de grupos que se comparan, la escala de medida de
las variables, el número de sujetos analizados, etc.
­(anexo 9). En este capítulo se presentan los funda­
mentos comunes a todas ellas, haciendo especial
énfasis en los aspectos relacionados con la inter­
pretación de los resultados obtenidos.
Supongamos que existe interés en comparar dos
tratamientos (un diurético D y el tratamiento es­
tándar E) para determinar cuál de ellos es el más
eficaz en el control de la presión arterial. Se diseña
un ensayo clínico, distribuyendo aleatoriamente
60 pacientes hipertensos en dos grupos, cada uno
de los cuales recibe uno de los tratamientos. A los
3 meses, el porcentaje de individuos controlados
en cada grupo es del 70 y el 50%, respectivamente.
¿Qué conclusión puede obtenerse a la vista de estos
256
resultados? ¿Hasta qué punto es posible que se deban
simplemente al azar (variaciones del muestreo) y que
en realidad no exista ninguna diferencia de eficacia
entre ambas intervenciones?
Hipótesis nula e hipótesis alternativa
Siguiendo con el ejemplo anterior, el análisis parte
de la hipótesis de que no existen diferencias entre los
porcentajes de hipertensos controlados observados
en ambos grupos. La prueba de significación es­
tadística intentará rechazar esta hipótesis, conocida
como hipótesis nula (Ho). Si se consigue, se aceptará
la hipótesis alternativa (Ha), según la cual existen
diferencias entre ambos grupos.
El primer paso es formular la Ho. A continuación se
calcula, mediante la prueba estadística más adecuada, la
probabilidad de que los resultados observados puedan
deberse al azar, en el supuesto de que la Ho sea cierta.
En otras palabras, la probabilidad de que, a partir de
una población de referencia, puedan obtenerse dos
muestras que presenten unos valores tan diferentes
como los observados simplemente por azar. Esta pro­
babilidad es el grado de significación estadística, que suele
representarse con la letra p. En tercer lugar, basándose
en esta probabilidad, se decide si se rechaza o no la
Ho. Cuanto menor sea la p, es decir, cuanto menor sea
la probabilidad de que el azar pueda haber producido
los resultados observados, mayor será la evidencia en
contra de la Ho y, por tanto, mayor será la tendencia a
concluir que la diferencia existe en la realidad.
Supongamos que, en el ejemplo, una vez aplicada
la prueba estadística adecuada, se obtiene un valor
de p aproximadamente de 0,10. Esto significa que, si
la Ho fuera cierta, la probabilidad de que el azar pue­
da producir unos resultados como los observados es
del 10%, es decir, que existe un 10% de probabilidad
de que dos muestras de 30 sujetos obtenidas de una
misma población presenten unos porcentajes del 70
y el 50% sólo por variabilidad aleatoria.
Para decidir si se rechaza o no la Ho, debe fijarse
previamente un valor de p por debajo del cual se con­
sidera que se dispone de la suficiente evidencia en su
contra para rechazarla. Este valor se conoce como valor
de significación estadística a. De forma arbitraria, y por
convenio, se fija habitualmente en el 5% (0,05).
Dado que el valor de p obtenido en el ejemplo es
de 0,10, superior al valor de significación de 0,05, se
considera que la probabilidad de haber obtenido es­
tos resultados por azar es demasiado elevada y que,
por tanto, no se dispone de la suficiente evidencia
para rechazar la Ho. De este modo, se concluye que
la diferencia observada en el porcentaje de pacientes
controlados no es estadísticamente significativa. No
significa que no exista diferencia en los porcentajes
Papel de la estadística
de ambos grupos, sino que no se ha encontrado la
suficiente evidencia para decir que son diferentes.
Supongamos ahora que en el grupo que recibió
el tratamiento E sólo se hubieran controlado 12 pa­
cientes a los 3 meses, lo que supondría un porcentaje
observado en este grupo del 40%. Si se repiten los
cálculos, se obtiene un valor de p < 0,02. Como este
valor es inferior a 0,05, se considera que la diferencia
observada es estadísticamente significativa, ya que
es poco probable (p < 5%) que el azar pueda haber
producido estos resultados. La respuesta a la pregun­
ta de si esta diferencia se debe al nuevo tratamiento
D dependerá del diseño y la ejecución correctos del
estudio. El valor de p sólo informa de la existencia
de una diferencia entre ambos grupos, y de que muy
probablemente no se deba al azar, pero no informa
sobre la causa de dicha diferencia.
El valor de p no es una medida de la fuerza de la
asociación. Un estudio en el que se obtenga un valor de
p < 0,001 no quiere decir que la asociación encontrada
sea más fuerte (o la diferencia más importante) que la
de otro estudio en que sea de 0,04. Sólo quiere decir que
es más improbable que su resultado sea por azar.
No hay que ser excesivamente rígido en el límite
del valor de significación. Un valor de p = 0,048 es
estadísticamente significativo con el umbral del 5%,
y uno de 0,052, en cambio, no lo es, pero en ambos
casos la probabilidad de observar el resultado por
azar es prácticamente la misma, y muy próxima
al 5%. Por ello, es conveniente indicar el valor de
p al dar los resultados, sobre todo si es próximo al
valor de significación, en lugar de limitarse a decir si
existe o no significación estadística. De esta forma, el
lector podrá valorar adecuadamente los resultados.
© Elsevier. Fotocopiar sin autorización es un delito.
Pruebas unilaterales y pruebas
bilaterales
En ocasiones, lo que interesa no es determinar si exis­
ten diferencias entre dos tratamientos, sino evaluar
si un nuevo fármaco es mejor que otro. En este caso,
la hipótesis alternativa no es que D y E difieran, sino
que D es mejor que E. Por tanto, la Ho que se va a
contrastar es que D no difiere o es peor que E. Dado
que sólo interesa un sentido de la comparación, se
habla de pruebas unilaterales, o de una cola.
¿Cómo afecta este hecho a la prueba de signifi­
cación? No es la prueba en sí misma la que se ve
afectada. El cálculo es idéntico al anterior. Lo que se
modifica es el valor de p. Como la distribución de Z
sigue la ley normal y, por tanto, es simétrica, en las
pruebas unilaterales el valor de p corresponde a la
mitad del valor a, dado que sólo se está interesado
en uno de los extremos.
Capítulo
| 27 |
Error a y error b
En estadística no puede hablarse de certeza absoluta.
Sea cual sea la decisión que se tome respecto a la
hipótesis nula, se corre un cierto riesgo de equivo­
carse (fig. 27.2).
La realidad no es conocida, ya que, si lo fuera, no
sería necesario realizar el estudio. Si no se rechaza
la Ho, y ésta es cierta, no se comete ningún error. Si
se rechaza y es falsa, tampoco. Pero ¿qué pasa en las
otras dos situaciones?
En un estudio puede concluirse que existe una di­
ferencia cuando en realidad no la hay. Es decir, puede
rechazarse la Ho cuando en realidad es cierta. Si esto
ocurre, la decisión es incorrecta y se comete un error,
conocido como error tipo I o error a. La probabilidad
de cometer este error es la de que, si se concluye que
existe una diferencia significativa, ésta sea en realidad
debida al azar. Si se hace un símil entre una prueba
estadística y una diagnóstica, equivale a la probabi­
lidad de obtener un resultado falso positivo. Esto es
precisamente lo que mide el valor de p, o grado de
significación estadística de la prueba.
Si, por el contrario, se concluye que la diferencia
no es estadísticamente significativa, es decir, si no se
rechaza la Ho, puede ocurrir que la hipótesis sea falsa
y que, en realidad, exista una diferencia entre ambos
grupos, en cuyo caso se cometerá otro tipo de error,
llamado error tipo II o b. Utilizando el símil con la
prueba diagnóstica, equivale a la probabilidad de
obtener un resultado falso negativo. Su valor com­
plementario 1 − b, denominado potencia, o poder
estadístico, indica la capacidad que tiene la prueba
para detectar una diferencia que existe en la realidad.
Lógicamente, cuanto mayor es la diferencia y más
elevado el número de individuos estudiados, mayor
capacidad existe para detectarla; es decir, el poder
estadístico es mayor y, por tanto, la probabilidad de
cometer un error b es menor.
Existe una interdependencia entre el grado de sig­
nificación p, la potencia estadística, el número de
individuos estudiados y la magnitud de la diferencia
observada. Conociendo tres de estos parámetros,
puede calcularse el cuarto. Así, antes de iniciar un
estudio, puede calcularse el número de sujetos ne­
cesario, fijando a priori el grado de significación, la
potencia estadística y el valor de la diferencia que
quiere detectarse. De igual modo, si una vez acabado
el estudio se concluye que no se ha encontrado una
diferencia estadísticamente significativa, dado que
n, p y la diferencia observada son conocidas, pue­
de calcularse el poder estadístico. No es lo mismo
concluir que no se ha encontrado una diferencia
estadísticamente significativa entre dos tratamientos
cuando se tiene una probabilidad del 90% de haberla
257
Parte
|4|
Interpretación de resultados
Figura 27.2 Resultados de una prueba de significación estadística.
detectado si hubiera existido (b = 0,10), que cuando
esta probabilidad es sólo del 20% (b = 0,20).
¿Diferencia estadísticamente
significativa o clínicamente relevante?
Un resultado estadísticamente significativo no im­
plica que sea clínicamente relevante. El valor de p no
mide la fuerza de la asociación. Pueden obtenerse
valores pequeños de p (resultados estadísticamente
significativos) simplemente estudiando un número
elevado de sujetos. Al aumentar el tamaño de la
muestra se incrementa el poder estadístico para
detectar incluso pequeñas diferencias.
Ejemplo 27.2. Supongamos un estudio en que se
comparan dos fármacos, D y E, para el tratamiento
de la hipertensión arterial. El porcentaje de pacientes
controlados en el grupo que ha recibido el fármaco
D es del 70%, y en el que ha sido tratado con E, del
65%. En la tabla 27.1 se aprecia que la conclusión de
si esta diferencia es o no estadísticamente significati­
va depende del número de individuos. Estudiando
30 pacientes en cada grupo, se concluiría que la dife­
258
rencia no es estadísticamente significativa. A medida
que aumenta el tamaño de los grupos, aumenta el va­
lor de Z y disminuye el de p. Al estudiar 700 pacientes
en cada grupo ya se alcanza el nivel de significación
estadística 9 del 0,05. Y si se estudiaran 2.000 indivi­
duos, el valor de p sería menor de 0,001.
La diferencia que se considera clínicamente rele­
vante depende de su magnitud y de otros factores,
como la frecuencia y la gravedad de los efectos
secundarios de ambos fármacos, la facilidad de
administración o su coste económico.
Estimación frente a significación
estadística
Al analizar los resultados de un estudio, los inves­
tigadores están interesados no sólo en saber si una
diferencia o una asociación son estadísticamente sig­
nificativas, sino también en determinar su magnitud.
La diferencia observada en el estudio es la mejor esti­
mación puntual de dicha magnitud. Pero, dado que
si se repitiera el estudio con otras muestras podrían
observarse resultados de diferente ­magnitud, hay que
Papel de la estadística
Capítulo
| 27 |
Tabla 27.1 Influencia del número de sujetos estudiados sobre el grado de significación estadística
de la comparación de los porcentajes de pacientes controlados con dos tratamientos: D (70%)
y E (65%) (ejemplo 27.2)
Número de sujetos estudiados por grupo
Valor de Z*
Valor de p
30
0,41
0,68
100
0,76
0,45
200
1,06
0,29
500
1,69
0,09
700
2,00
0,05
1.000
2,39
< 0,02
2.000
3,38
< 0,001
© Elsevier. Fotocopiar sin autorización es un delito.
*Valor de la Z de comparación de dos proporciones.
calcular un intervalo del que se tenga una determinada
confianza de que contiene la verdadera magnitud del
parámetro de interés, tanto si se trata de una diferencia
(cuadros 27.3 y 27.4) como de una medida de asocia­
ción (anexo 2). Existen fórmulas para el cálculo de los
IC en cualquier situación.
Cuando se utiliza como medida del efecto una
diferencia, si el IC del 95% incluye el valor 0, que es el
que corresponde a la Ho (ausencia de diferencia entre
ambos grupos), se concluirá que el resultado no es
estadísticamente significativo, ya que no puede des­
cartarse que ése sea el verdadero valor. Si, por el con­
trario, el IC excluye este valor 0, se concluirá que la
diferencia observada es estadísticamente significativa,
ya que puede descartarse dicho valor (con un riesgo
de error inferior al 5%). Por tanto, el IC, además de
indicar si la diferencia es o no estadísticamente signi­
ficativa, permite conocer entre qué límites es probable
que se encuentre la verdadera diferencia, lo que es
muy útil en la interpretación de los resultados.
Ejemplo 27.3. Supongamos un estudio que com­
para la eficacia de dos tratamientos A y B en dos
grupos de 30 pacientes. Se observa una diferencia
en el porcentaje de éxitos del 20% (70 – 50%) a
favor del tratamiento B, que no es estadísticamente
significativa (p = 0,12). El IC del 95% de la diferencia
entre los dos tratamientos es:
IC 95%: 0,2±0,24; es decir, de − 4a 44%
Con un 95% de confianza, la verdadera magnitud
de la diferencia está en el intervalo comprendido en­
tre un 4% a favor del tratamiento A y un 44% a favor
de B. Dado que una diferencia del 0% es ­posible, no
puede descartarse que éste sea su verdadero valor,
por lo que el resultado no es estadísticamente sig­
nificativo. En cambio, el IC informa, además, que
también son posibles grandes diferencias a favor de B,
y que son improbables grandes diferencias a favor de
A. Aunque los resultados siguen sin ser concluyentes,
se dispone de más información para interpretarlos de
forma adecuada. El IC cuantifica el resultado encon­
trado y provee un rango donde es muy probable que
se encuentre el valor real que se está buscando.
Ejemplo 27.4. Supongamos un estudio que compara
la eficacia de dos tratamientos A y B en dos grupos
de 80 pacientes. Se observa una diferencia del 5%
(65 − 60%) a favor del tratamiento B, que es esta­
dísticamente significativa (p = 0,04). El IC del 95%
de esta diferencia es:
IC 95%: 0,05±0,047; es decir, de 0,3 a 9,7%
Al excluir el valor 0% se concluye que la diferencia
es estadísticamente significativa. El IC informa que la
diferencia es de pequeña magnitud, como máximo
de aproximadamente un 10% a favor de B.
Los IC tienen otra ventaja adicional, y es que ex­
presan los resultados en las unidades en que se han
realizado las mediciones, lo que permite al lector
considerar críticamente su relevancia clínica.
Al diseñar un estudio, los autores establecen la
magnitud mínima de la diferencia que consideran
de relevancia clínica, en función de la cual han cal­
culado el tamaño necesario de la muestra. Al acabar
el estudio, la interpretación del resultado observa­
do y de su IC debe tener en cuenta también esta
magnitud. Además de determinar si el IC del 95%
excluye el valor 0 para saber si el resultado es estadís­
ticamente significativo, también debe ­determinarse
259
Parte
|4|
Interpretación de resultados
Cuadro 27.3 Cálculo del intervalo
de confianza (IC)
de la diferencia entre
dos proporciones
IC de la diferencia de dos proporciones*
a) Muestras independientes
Cuadro 27.4 Cálculo del intervalo
de confianza (IC) de la
diferencia entre dos medias
IC de la diferencia de dos medias*
a) Muestras independientes
(x– −x– ) ± Za⋅EED
A
(PA−PB) ± Za⋅EED
________
√
_________________
siendo EED = s⋅​ __
​ n1  ​ + __
​ n1  ​ ​ 
___________________
√
P ⋅(1−P ) _______
P ⋅(1−PB)
siendo EED = ​ ________
​  A n   A  
​ 
+ ​  B n  
   
 
​ ​
A
√
_______________
Las variables cualitativas no presentan una distribución
normal. Las fórmulas de la tabla corresponden
a una aproximación a la normalidad, aplicable cuando
todos los productos n·PA·n·(1 − PA), n·PB y n·(1 − PB)
son mayores de 5. En caso contrario, deben aplicarse
correcciones en el valor de Za.
*
si incluye o excluye el valor de la mínima diferencia
de relevancia clínica, para poder evaluar si el es­
tudio es concluyente acerca de la existencia de una
diferencia clínicamente importante.
Ejemplo 27.5. En la figura 27.3 se presentan seis posi­
bles resultados de un estudio que compara dos gru­
pos y utiliza como medida del resultado la diferencia
entre los porcentajes observados en cada uno de ellos.
Supongamos que los investigadores establecieron a
priori que la mínima diferencia de relevancia clínica
era del 20%.
Situación A. Se observa una diferencia del 10% (IC
95%: −5 a +25%), que no es estadísticamente signifi­
cativa, ya que el IC incluye el valor 0. Pero el valor 20%
también es un valor posible, ya que está situado en el
interior del IC. Se trata, por tanto, de un resultado que
no permite descartar ninguna conclusión.
Situación B. En esta ocasión se observó una diferen­
cia entre los grupos del 5% (IC 95%: −5 a +15%). No
es estadísticamente significativa, ya que el IC incluye
260
d
(b − c)2
PA, PB: proporciones observadas en las muestras A y B.
nA, nB: número de sujetos de las muestras A y B.
b, c: número de casos que presentan valores
diferentes en ambas mediciones (series
apareadas).
n: número total de casos.
EED: error estándar de la diferencia.
Za: valor de la variable normal tipificada
correspondiente al valor a, para un nivel
de confianza (1 − a).
2
B
2
A
B
 ​b) Muestras apareadas
x– ± Za⋅EEx–
(PA−PB) ± Za⋅EED
1 ​​ b + c − ______
siendo EED = ​ __
​  n  
   
 
​ ​
n
A
sA (nA−1) + sB (nB−1)
y s = ​ ​ _______________
  
  
   ​
n + n −2
B
b) Muestras apareadas
√
B
d
x–A,x–B: medias observadas en las muestras A y B.
sA, sB: desviaciones estándar observadas
en las muestras A y B.
nA, nB: número de sujetos de las muestras A y B.
EED: error estándar de la diferencia.
x–d: media de las diferencias de las dos mediciones
en cada individuo (series apareadas).
EEx–d: error estándar de la media de las diferencias
individuales.
Za: valor de la variable normal tipificada
correspondiente al valor a, para un nivel
de confianza (1 − a).
El cálculo se basa en la distribución normal. El valor
de Za para un IC del 95% es 1,96. Para muestras de tamaño
inferior a 30 individuos, este valor debe sustituirse
por el de la t de Student para (n − 1) grados de libertad.
Así mismo, el cálculo requiere que no existan diferencias
significativas entre las desviaciones estándar de ambas
muestras.
*
el valor 0, pero excluye el valor 20%. Así pues, el
resultado es negativo en el sentido de que no puede
descartarse que los grupos sean iguales, pero, aunque
fueran diferentes, es muy improbable que la diferen­
cia sea mayor del 15%. Por tanto, puede descartarse
que exista una diferencia de relevancia clínica.
Situación C. La diferencia observada del 10% (IC
95%: +5 a +15%) es estadísticamente significativa,
ya que el IC excluye el valor 0. Dado que el límite
superior del IC no alcanza el valor 20%, puede con­
cluirse que existe una diferencia, pero que ésta no es
de relevancia clínica.
Situación D. La diferencia observada es del 15%
(IC 95%: +5 a +25%), estadísticamente significativa
y potencialmente importante, ya que el valor 20%
es un valor posible. Así pues, el estudio no es del
todo concluyente.
Situación E. Similar a la anterior. Aunque la dife­
rencia observada es mayor del 20%, el resultado no
es del todo concluyente, ya que el límite inferior del
Papel de la estadística
Capítulo
| 27 |
© Elsevier. Fotocopiar sin autorización es un delito.
Figura 27.3 Posibles resultados de un estudio que compara dos grupos y utiliza como medida del efecto
la diferencia entre los porcentajes observados. Se considera que la mínima diferencia de relevancia
clínica es del 20% (ejemplo 27.5).
IC está por debajo del 20% e indica que la verdadera
diferencia podría ser inferior a este valor.
Situación F. La diferencia observada es del 30%.
Dado que el límite inferior del IC es mayor del 20%,
este resultado es estadísticamente significativo y
concluyente a favor de la existencia de una diferencia
de relevancia clínica.
Cuando se utiliza una medida relativa del efecto
(riesgo relativo, odds ratio, etc.), la Ho de igualdad
entre los grupos corresponde al valor 1, ya que se
trata de un cociente y no de una diferencia. Por
tanto, cuando el IC del 95% de una medida relativa
incluye el valor 1, el resultado no es estadísticamente
significativo.
Aunque las pruebas de significación continúan
siendo los procedimientos estadísticos más emplea­
dos, las ventajas de la utilización complementaria de
los IC en el análisis e interpretación de los resulta­
dos, tanto si el objetivo es la estimación de paráme­
tros como el contraste de una hipótesis, hacen que
cada vez se les conceda una mayor importancia y
las directrices para la publicación de estudios cien­
tíficos recomiendan que se presenten los resultados
principales con su correspondiente IC en lugar de
informar solamente del valor de p.
Comparaciones múltiples
En cualquier estudio se realizan habitualmente múl­
tiples comparaciones; por ejemplo, cuando se evalúa
si los grupos difieren por alguna variable, cuando
se comparan diferentes variables de respuesta o
cuando se analizan diversos subgrupos de sujetos.
Efectuar comparaciones múltiples tiene dos grandes
inconvenientes:
• La realización de pruebas para cada variable por
separado ignora el hecho de que muchas de ellas
pueden estar relacionadas entre sí, de forma que
el resultado de una prueba estadística determi­
nada puede estar influido por diferencias en la
distribución de otras variables relacionadas.
• Si cada una de las pruebas estadísticas se realiza
con el nivel de significación prefijado del 5%, en
promedio, 5 de cada 100 comparaciones pueden
resultar significativas sólo por azar. Al realizar
múltiples comparaciones, aumenta la probabili­
dad de obtener algún resultado estadísticamente
significativo que no refleje una diferencia real.
Para estimar la probabilidad de obtener un resul­
tado significativo por azar tras realizar un número
n de pruebas estadísticas, cada una de ellas con el
nivel de significación a, puede usarse la llamada
desigualdad de Bonferroni, de la que se deriva la si­
guiente fórmula:
Pr = 1−(1−a)n
donde Pr representa la probabilidad de encontrar
un resultado significativo.
261
Parte
|4|
Interpretación de resultados
Ejemplo 27.6. Supongamos que se realizan 8 com­
paraciones independientes, cada una de ellas con
el nivel de significación de 0,05. La probabilidad
de que alguna de estas comparaciones conduzca a
un resultado significativo simplemente por azar es:
Pr = 1−(1−0,05)8 = 0,336
es decir, existe un 33% de probabilidades de come­
ter algún error a, y no el 5% con el que se deseaba
trabajar.
Puede utilizarse como aproximación el producto
del valor de significación por el número de pruebas
realizadas (n·a). En el ejemplo, este valor sería 0,40,
que, como puede observarse, sobrestima ligeramente
dicha probabilidad.
La solución más adecuada a este problema es
reducir en lo posible el número de comparaciones
que realizar, y aplicarlas solamente para contrastar
hipótesis previas, y asignar prioridades antes del aná­
lisis, para decidir cuál es la comparación principal y
cuáles las secundarias, de forma que estas últimas se
utilicen para matizar la respuesta a la primera.
Otra solución es dividir el valor de significación
deseado por el número de pruebas que se van a rea­
lizar y obtener así un valor de significación corregido
para aplicarlo a cada una de las pruebas. Este procedi­
miento se conoce como corrección de Bonferroni. En el
ejemplo 27.6, si se desea mantener el valor de signifi­
cación global del 0,05, cada una de las pruebas deberá
realizarse con el valor corregido de 0,05/8 = 0,00625.
La corrección de Bonferroni asume que las compa­
raciones son independientes, por lo que no resulta
adecuada cuando los análisis están mutuamente
asociados.
Ejemplo 27.7. Supongamos que un estudio utiliza
como variable principal la variación en los valores de
hemoglobina, y se observa una reducción estadística­
mente significativa. Al analizar también los valores
de hematocrito, también se obtiene una disminución
significativa, pero al aplicar la corrección de Bonfe­
rroni, la reducción de la hemoglobina deja de ser
estadísticamente significativa. Este hecho no parece
lógico, ya que realmente la variación del hematocrito
estaría confirmando el resultado principal. El proble­
ma es que las comparaciones no son independientes,
ya que se trata de parámetros muy correlacionados
(como el hematocrito y la hemoglobina), de manera
que si el resultado es significativo en uno de ellos, es
probable que lo sea también en el otro.
El inconveniente principal de la corrección de
Bonferroni es que protege excesivamente contra la
­posibilidad de rechazar de forma errónea alguna
de las hipótesis nulas a costa de disminuir la poten­
262
cia de la prueba. Dado que el intento de ajustar el
efecto de la multiplicidad de análisis podría requerir
establecer niveles de significación estadística absur­
damente pequeños, parece más razonable adoptar
una actitud conservadora al interpretar los resultados
de análisis múltiples y valorar su consistencia entre
las diferentes variables. Una vez más, lo ideal sería
definir a priori la variable principal y unas pocas
variables secundarias como protección frente a este
problema. No sería lógico que la interpretación de los
resultados observados fuera diferente según el núme­
ro de pruebas estadísticas que se llevan a cabo. Si, por
ejemplo, se comparan dos pautas de quimioterapia
y se observa una diferencia en las tasas de remisión,
el hecho de considerarla o no estadísticamente sig­
nificativa no debería depender de si se han evaluado
además otros parámetros, como la supervivencia, las
complicaciones o la calidad de vida.
De hecho, existen opiniones contrarias al uso
rutinario de este ajuste, fundamentalmente cuando
se trata de múltiples resultados, aunque parece más
adecuado su uso cuando se comparan diferentes
subgrupos o se realizan análisis secuenciales. Una al­
ternativa más adecuada es el empleo de técnicas mul­
tivariantes que tomen en consideración las relaciones
que existen entre las variables que se comparan.
Un problema similar puede presentarse en es­
tudios con un seguimiento prolongado, cuando el
investigador decide analizar sus datos repetidamente
a medida que el estudio progresa. El uso del valor
de significación estadística según el método habitual
no resulta apropiado, ya que el cálculo convencional
asume que el tamaño de la muestra es un valor fijo,
y que los resultados del estudio se analizarán una
única vez con los datos de todos los sujetos. Por
tanto, si un investigador analiza los datos en diversas
ocasiones, la probabilidad de alcanzar un resultado
significativo es mayor que la deseada. Cuando se
efectúa este tipo de estudios, lo mejor es utilizar un
diseño secuencial, en el que no es necesario asumir
que el análisis se realizará una sola vez, y en el que
las normas para finalizar el estudio permiten la
evaluación continuada de los datos.
Análisis multivariante
Hay veces en las que interesa considerar la influen­
cia de más de dos variables simultáneamente. Ello
requiere técnicas sofisticadas, basadas en modelos
matemáticos complejos, agrupadas bajo el nombre
genérico de análisis multivariante.
Existen múltiples técnicas estadísticas multivarian­
tes. En investigación clínica y epidemiológica, las más
utilizadas son las que analizan la relación entre una
variable dependiente (variable de respuesta) y un grupo
Papel de la estadística
de variables independientes (factor de estudio y varia­
bles que controlar). Estas técnicas implican la cons­
trucción de un modelo matemático. La elección de un
modelo u otro dependerá del diseño del estudio, la
naturaleza de las variables y las interrelaciones entre
el factor de estudio, la variable de respuesta y las res­
tantes variables incluidas en el modelo (anexo 9).
Estas técnicas pueden aplicarse con las siguientes
finalidades:
• Proporcionar una estimación del efecto de una
variable independiente principal (factor de
­estudio) sobre una dependiente (variable de res­
puesta), ajustada por un conjunto de factores o
variables independientes (potenciales factores de
confusión y modificadores del efecto).
Ejemplo 27.8. Supongamos un ensayo clínico
aleatorio que evalúa el efecto de un nuevo fármaco
(variable independiente principal) sobre la coleste­
rolemia (variable dependiente), controlando la in­
fluencia de la edad y el sexo de los sujetos (variables
independientes).
• Describir la relación que existe entre un conjunto
de variables independientes (sin identificar una de
ellas como principal) y una variable dependiente, y
la contribución de cada una de ellas a la relación.
Ejemplo 27.9. Supongamos un estudio transversal
que pretende evaluar, de entre un conjunto de varia­
bles independientes (colesterol, edad, sexo, gluce­
mia, etc.), cuáles están asociadas con una variable
dependiente (cifras de presión arterial).
• Predecir el valor de una variable dependiente en
© Elsevier. Fotocopiar sin autorización es un delito.
función de los valores que toma un conjunto de
variables independientes.
Ejemplo 27.10. Supongamos un estudio de cohortes
en el que se desea obtener una ecuación que prediga
el riesgo cardiovascular (variable dependiente) en
función de la edad, el sexo, las cifras de presión ar­
terial, el consumo de tabaco y las cifras de colesterol
de los sujetos (variables independientes).
Las técnicas que relacionan un conjunto de varia­
bles independientes con una dependiente derivan
del modelo de regresión lineal, y pueden clasificarse
a partir de la escala de medida de la variable depen­
diente (anexo 9).
Cuando la finalidad del análisis es predictiva o
descriptiva de las relaciones entre variables, lo que
interesa es obtener una ecuación o un modelo lo
más sencillo posible, de forma que la selección de las
variables que formarán el modelo se basa en criterios
Capítulo
| 27 |
de significación estadística. En cambio, cuando la
finalidad es estimar el efecto del factor de estudio
controlando determinados factores de confusión,
no puede confiarse en que la selección automática in­
cluya las variables que interesa controlar, ya que no
siempre están asociadas de forma estadísticamente
significativa, por lo que se utilizan otros procedi­
mientos que obligan a la selección por parte del
investigador de las variables que desea controlar.
La correcta utilización de la estadística en el aná­
lisis de los datos es fundamental para poder inter­
pretarlos de forma adecuada y obtener conclusiones
válidas. Por ello, una vez realizado el análisis multi­
variante, hay que evaluar la adecuación del modelo
obtenido (bondad de ajuste), ya que, por ejemplo,
una ecuación puede ser estadísticamente significa­
tiva, pero predecir con poca fiabilidad el riesgo de
enfermar de un sujeto. Debe prestarse atención a
las medidas globales de bondad del modelo, así
como comprobar si se cumplen las condiciones de
aplicación de cada una de las técnicas.
También en las técnicas multivariantes, el resultado
obtenido es una estimación puntual, por lo que de­
berá calcularse el correspondiente IC para evaluar su
relevancia clínica. Todos los comentarios realizados
a propósito de la significación estadística y la relevan­
cia clínica en las pruebas estadísticas bivariantes son
aplicables a las multivariantes. La principal diferencia
es que en el análisis multivariante se tienen en cuenta
simultáneamente las relaciones entre múltiples varia­
bles, de forma que una ecuación predictiva mejorará
su capacidad de predicción al incorporar más de una
variable o la estimación del efecto del factor de estudio
estará ajustada, es decir, se habrá controlado el efecto
simultáneo de diferentes factores de confusión.
En otras ocasiones no puede diferenciarse entre
variables dependientes e independientes, sino que,
de acuerdo con el objetivo del estudio, el análisis
persigue finalidades diferentes, como la clasificación
de variables o individuos aparentemente heterogéneos
en grupos homogéneos, según un conjunto de datos
(análisis de conglomerados o cluster analysis), o la
identificación de los factores subyacentes en un con­
junto de variables, es decir, la reducción de la dimen­
sionalidad de los datos, combinando un conjunto am­
plio de variables observadas en unas pocas variables
ficticias (combinaciones lineales de las anteriores) que
representen casi la misma información que los datos
originales (análisis factorial y análisis de componentes
principales). Estas técnicas se utilizan con frecuencia
en la investigación sobre servicios sanitarios, pero
poco en investigación clínica y epidemiológica.
Ejemplo 27.11. Supongamos que se desea desarro­
llar un indicador del estado de salud aplicable a
263
Parte
|4|
Interpretación de resultados
diferentes regiones. Para ello, se recogen multitud
de indicadores sanitarios, demográficos, sociales,
etc., de estas regiones, y se aplica una técnica multi­
variante para reducir todos estos indicadores a unas
pocas variables ficticias, con la extracción de ­factores,
cada uno de los cuales representa una dimensión
de la información contenida en la totalidad de los
indicadores.
Bibliografía
Altman DG, Bland JM. Parametric
vs non-parametric methods
for data analysis. BMJ.
2009;338:a3167.
Altman DG. Missing outcomes in
randomized trials: addressing
the dilemma. Open Med.
2009;3(2):e51-3.
Altman DG, Bland JM. Missing
data. BMJ. 2007;334:424.
Altman DG, Royston P. The cost
of dichotomising continuous
variables. BMJ. 2006;332:1080.
Altman DG, Bland JM. Standard
deviations and standard errors.
BMJ. 2005;331:903.
Altman D, Bland JM. Confidence
intervals illuminate absence of
evidence. BMJ. 2004;328:1016-7.
Argimon JM. La ausencia de
significación estadística en
un ensayo clínico no significa
equivalencia terapéutica. Med
Clin (Barc). 2002;118:701-3.
Argimon JM. Intervalos de
confianza: algo más que un valor
de significación estadística. Med
Clin (Barc). 2002;118:382-4.
Armitage P, Berry G, Matthews JNS.
Statistical methods in medical
research. 4.ª ed.. Oxford:
Blackwell Science; 2002.
Bayarri MJ, Cobo E. Una
oportunidad para Bayes. Med
Clin (Barc). 2002;119:252-3.
Bland JM. The tyranny of power:
is there a better way to
calculate sample size? BMJ.
2009;339:b3985.
Bland JM, Altman DG. Analysis
of continuous data from small
samples. BMJ. 2009;338:a3166.
Bland JM, Altman DG. The logrank
test. BMJ. 2004;328:1073.
Boutron I, Dutton S, Ravaud P,
Altman DG. Reporting and
interpretation of randomized
controlled trials with
statistically nonsignificant
264
results for primary outcomes.
JAMA. 2010;303(20):2058-64.
Bland JM, Altman DG. Survival
probabilities (the Kaplan-Meier
method). BMJ. 1998;317:1572.
Bender R, Lange S. Adjusting
for multiple testing-when
and how? J Clin Epidemiol.
2001;54:343-9.
Bradburn MJ, Clark TG, Love SB,
Altman DG. Survival Analysis
Part II: Multivariate data
analysis – an introduction to
concepts and methods. Br J
Cancer. 2003;89:431-6.
Clark TG, Bradburn MJ, Love SB,
Altman DG. Survival Analysis. Part
I. Basic concepts and first analysis.
Br J Cancer. 2003;89:232-8.
Cobo E, Muñoz P, González
JA, editors. Estadística para
no estadísticos: bases para
interpretar artículos científicos.
1ª ed. Barcelona: Elsevier; 2007.
Cobo E. Análisis multivariante
en investigación biomédica:
criterios para la inclusión de
variables. Med Clin (Barc).
2002;119:230-7.
Cohen HW. P values: use and
misuse in medical literature.
Am J Hypertens. 2011;24:18-23.
Doll H, Carney S. Introduction to
biostatistics: Part 3. Statistical
approaches to uncertainty:
P values and confidence
intervals unpacked. ACP J Club.
2006;144:A8-9.
Katz MH. Multivariable analysis:
a primer for readers of medical
research. Ann Intern Med.
2003;138:644-50.
Moss M, Wellman DA, Cotsonis GA.
An appraisal of multivariable
logistic models in the pulmonary
and critical care literature. Chest.
2003;123:923-8.
Nüesch E, Trelle S, Reichenbach S,
Rutjes AW, Bürgi E, Scherer M,
et al. The effects of excluding
patients from the analysis in
randomised controlled trials:
meta-epidemiological study.
BMJ. 2009;339:b3244.
Perneger TV. What’s wrong with
Bonferroni adjustments. BMJ.
1998;316:1236.
Pocock SJ, Ware JH. Translating
statistical findings into plain
English. Lancet. 2009;373:1926-8.
Pocock SJ, Travison TG, Wruck
LM. How to interpret figures in
reports of clinical trials. BMJ.
2008;336:1166-9.
Pocock SJ. The simplest statistical
test: how to check for a
difference between treatments.
BMJ. 2006;332:1256-8.
Royston P, Altman DG. Visualizing
and assessing discrimination in
the logistic regression model.
Stat Med. 2010;29(24):2508-20.
Stone GW, Pocock SJ. Randomized
trials, statistics, and clinical
inference. J Am Coll Cardiol.
2010;55:428-31.
Schulz KF, Grimes DA. Multiplicity
in randomised trials II:
subgroup and interim analyses.
Lancet. 2005;365:1657-61.
Schulz KF, Grimes DA. Multiplicity
in randomised trials I:
endpoints and treatments.
Lancet. 2005;365:1591-5.
Streiner DL, Norman GR.
Correction for multiple testing:
is there a resolution? Chest.
2011;140:16-8.
Vedula SS, Altman DG. Effect
size estimation as an
essential component of
statistical analysis. Arch Surg.
2010;145:401-2.
White IR, Horton NJ, Carpenter J,
Pocock SJ. Strategy for intention
to treat analysis in randomised
trials with missing outcome
data. BMJ. 2011;342:d40.