10. Practicas AO 10, 11 y 13

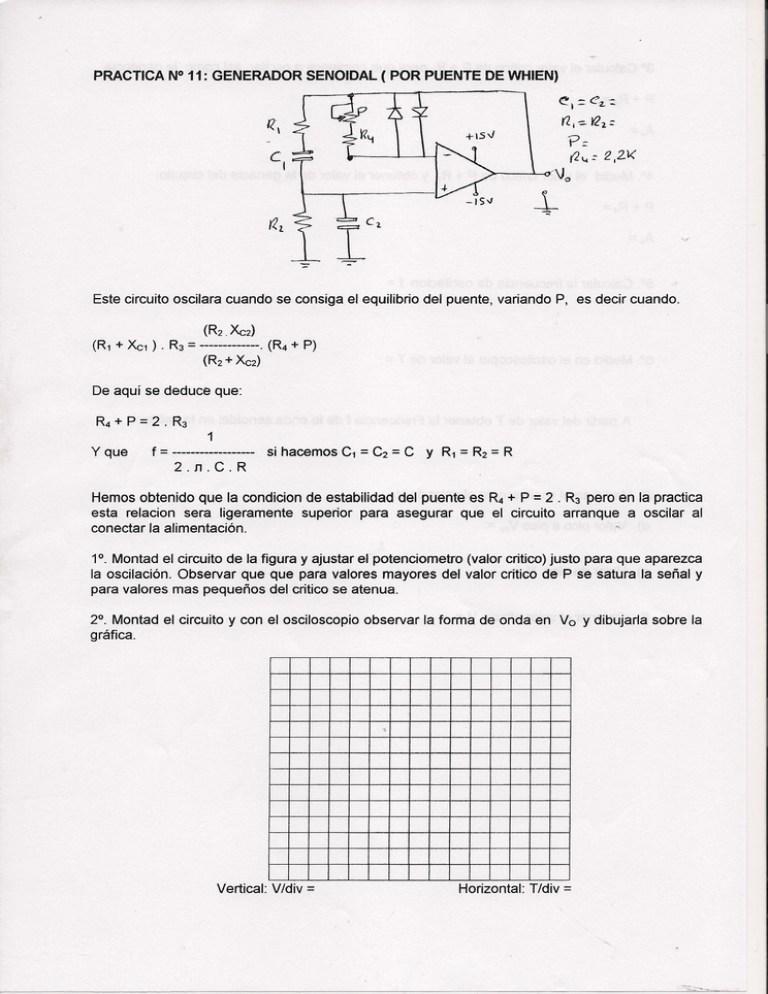
PRACTICA N° 11: GENERADOR SENOIDAL ( POR PUENTE DE WHIEN)
el.::ez..~
rzj-=-~2.=
p=
R\
eI
(2\.t =-
2,21<'
Este circuito oscilara cuando se consiga el equilibrio del puente, variando P, es decir cuando.
(R2.Xc2)
(R1 + Xc1 ) . R3
= -------------. (R4 + P)
(R2 + Xc2)
De aquí se deduce que:
1
Y que
f
= ------------------
si hacemos C1
= C2 = C
y R1
= R2 = R
2.fl.C.R
=
Hemos obtenido que la condicion de estabilidad del puente es R4 + P 2 . R3 pero en la practica
esta relacion sera ligeramente superior para asegurar que el circuito arranque a oscilar al
conectar la alimentación.
-,
1°. Montad el circuito de la figura y ajustar el potenciometro (valor critico) justo para que aparezca
la oscilación. Observar que que para valores mayores del valor critico de P se satura la señal y
para valores mas pequeños del critico se atenua.
2°. Montad el circuito y con el osciloscopio observar la forma de onda en Va Y dibujarla sobre la
gráfica.
Vertical: V/div =
Horizontal: T/div
=
~
3° Calcular el valor critico de P + ~ para que comience a oscilar, asi como la ganancia
A.., =
4°. Medid el valor critico de P + R4 Y obtener el valor d~ la ganacia del circuito:
A v--
f
=
6°. Medid en el osciloscopio el valor de T
=
5°. Calcular la frecuencia de oscilacion
A partir del valor de T obtener la Frecuencia f de la onda senoidal en la salida
7°. Medid en el osciloscopio el valor de
d) Valor pico a pico Vpp
=
e) Valor de pico Vp =
f)
Obtener el valor eficaz V =
v;
PRACTICA N° 10: GENERADOR SENOIDAL (Re POR DESPLAZAMIENTO
DE FASE)
e \--c2---c .•
.••--Iol"lf
~\..: rZ.z.
= ((1 :
p11;:::
,">-_.L...---o
22oi(..Jj.
Vo
Este oscilador se basa en el desfase introducido por un conjunto de celulas RC identicas
conectado como realimentación (R1-C1, R2-C2. R3-C3) mas un amplificador inversor formado por
R3 , R4 +P Y el A.O.
Mediante las tres celulas se obtiene un desfase de 1800 en la red de realimentación, siendo este
el mJnimo nOde células capaces de obtener este desfase. Haciendo R1 = R2 = R3 = R Y C1 = C2
C3 C, se demuestra que la frecuencia de la oscilacion generada es:
=
=
1
f = --------------------------- siendo N el numero de celulas R-C
2. n . C . R . .J2.N
Igualmente la gananacia del circuito ha de ser 29, debiendo cumplirse que
1°. Montad el circuito de la figura y ajustar el potenciometro (valor critico) justo para que aparezca
la oscilación. Observar que que para valores mayores del valor critico de P se satura la señal y
para valores mas pequeños del critico se atenua.
2°. Montad el circuito y con el osciloscopio observar la forma de onda en Vo y dibujarla sobre la
gráfica.
Vertical: V/div
=
Horizontal: T/div =
3° Calcular el valor critico de P + R4 para que comience a oscilar, asi como la ganancia
P+ R4=
Av=
4°. Medid el valor critico de P + R4 Y obtener el valor de la ganacia del circuito:
P + R4=
Av=
f
=
6°. Medid en el osciloscopio el valor de T
=
5°. Calcular la frecuencia de oscilacion
A partir del valor de T obtener la Frecuencia f de la onda senoidal en la salida
7°. Medid en el osciloscopio el valor de Va
a) Valor pico a pico Vpp
b) Valor de pico Vp
=
=
c) Obtener el valor eficaz V
=
PRACTICA N°13: OSCILADOR CONTROLADO POR TENSION (V.C.O.)
ESQUEMA:
e
, +Vcc
J
MATERIALES:
Vcc= +15V -Vcc= -15V
A1= A2= A3= uA741
Q=BC547
(
t-:.
ti.
v¿.
i
'-,,--'
2 \).:.<: . ¡J<s e
R1 = R2= R3= R4= R5= R7= ~8= 12Kohm
R6= 100KohlTi
C = 10nF
POLI METRO
OSCILOSCOPIO
MEDIDAS EN EL. CIRCUITO:
Dibujar sobre la misma gráfica (con colores diferentes) Las tensiones en Vi, V1, V2 y Vo
1°: Para Vi=+1V
Vertical: Vldiv=
Horizontal TempolDiv=
Vertical: Vldiv=
Horizontal TempolDiv::
Vertical: Vldir-
Horizontal TempolDir-
Vertical: Vldiv=
Horizontal TempolDiv=