) () ( TT T T TT Q Q Q − − − − = − = η T T T T r r = = = = λ

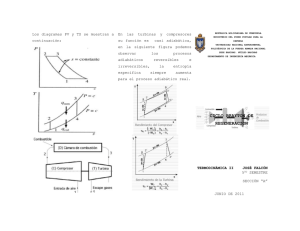
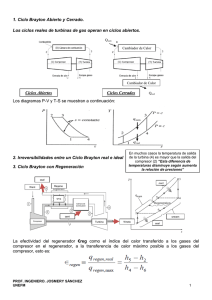
UNIDAD 9
TURBINA DE GAS – CICLO BRAYTON Y OTROS
1.
Introducción
La así llamada turbina de gas es una turbomáquina de combustión interna que consta de un compresor dinámico (axial o
centrífugo), una o más cámaras de combustión, y una turbina (axial o centrífuga).
La figura siguiente ilustra la disposición típica, incluyendo el motor eléctrico de arranque (que actúa sobre el eje a
través de engranajes a 90º) y la tobera de escape (con un cono ajustable)
Fig. 9-1: Turbina de gas (Lancaster)
La turbina ilustrada opera según el ciclo de Brayton simple. Otras configuraciones operan según ciclos de Brayton
regenerativo y regenerativo con calentamiento.
2.
Ciclo Brayton simple ideal:
La entrega de calor por el combustible se realiza a presión constante.
El ciclo es abierto (el fluido de trabajo no recircula), por lo que el diagrama de ciclo se completa con una línea a presión
constante (atmosférica) del escape a la admisión:
Fig. 9-2: Ciclo Brayton, plano t,i-s
1-2: Compresión
2-3: Combustión
3-4: Expansión
4-1: Escape
Fig 9-3: Ciclo Brayton, plano p-v
Como las transferencias de calor son a presión constante Q = ∆i = Cp∆t, y asumiendo Cp=cte
ηB,t =
Si denominamos rp =p 2 /p 1 y rv =V2 / V1 , llamamos
Q1 − Q2 (T3 − T2 ) − (T4 − T1 )
=
Q1
T3 − T2
γ −1
λ = r p γ = rvγ −1 =
T2 T3
=
T1 T4
se llega a
117
ηB , t = 1 −
T1
1
1
= 1 − γ −1 = 1 − γ −1
T2
rv
rp γ
ηB , t = 1 −
1
λ
El rendimiento del ciclo Brayton teórico sólo depende de la relación de compresión, y no depende del calor
suministrado.
Si comparamos con el ciclo de Carnot entre los mismos límites:
ηc = 1 −
T1
T3
vemos que el ciclo Brayton aumenta su rendimiento y se aproxima al de Carnot a medida que aumenta la compresión (y
disminuye el calor entregado):
Fig 9-4: Ciclo Brayton, T2 → T3
Por otra parte, si T2 → T1 , ηB,t → 0. Luego, habrá un valor de T2 entre T1 y T3 que maximice el área del ciclo, y el
trabajo. El trabajo útil es
L = Q1 − Q2 = c p [(T3 − T2 ) − (T4 − T1 ) ]
Reemplazamos
T4 T3
∂L
=
y hacemos
= 0 , obteniendo
T1 T2
∂T2
T2 = T1 ⋅ T3
Gráficamente:
Fig. 9-5: Limites de T2
a : T2 → T3 , ηB,t → ηC , L → 0
T
b : T2 = T1T3 , ηB,t → 1 − 1 , L → max
T3
c : T1 → T2 , ηB,t → 0, L → 0
118
El rendimiento del ciclo Brayton simple es bajo, por lo que sólo se lo utiliza donde no se puede mejorar por medio de la
regeneración o recalentamiento.
3.
Ciclo Brayton simple, real
Asumimos ahora compresión y expansión con aumento de entropía:
Fig. 9-6: Ciclo real
Definimos los rendimientos de compresor y turbina (expansor) como
T2 − T1
T2 ' − T1
T − T4 '
ηe = 3
T3 − T4
ηc =
y la relación σ= T3 /T1
El trabajo de compresión:
Lc = c p (T2 ' − T1 ) =
cp
ηc
(T2 − T1 ) =
cp
ηc
⋅ T1 ⋅ ( λ − 1)
El trabajo de expansión (turbina):
1
1
Le = c p (T3 − T4 ' ) = c p ηe (T3 − T4 ) = c pηeT3 1 −  = c pηeσT1  1 − 
 λ
 λ
Con esto, el trabajo útil o neto es:
1  cp
1
λ


 λ − 1 
Lu = Le − Lc = c p T1ηeσ 1 −  − T1 λ 1 −  = c p T1 
ηeσ − 
ηc 
 λ  ηc
 λ
 λ 
El calor aportado es
Q1 = c p (T3 − T2 ' ) = (σT1 − T2 ' )
De
ηc =
 λ −1 
T2 − T1
T −T
→ T2' = 2 1 + T1 = T1 
+ 1
T2 ' − T1
ηc
η
 c

Luego

 λ − 1 

λ − 1
Q1 = c p σT1 − T1 
+ 1  = c p T1 (σ − 1) −
ηc 

 ηc
 

Y el rendimiento
ηB , r
(
)
ηe σ − ηλc
Lu λ − 1
=
=
⋅
Q1
λ (σ − 1) − λη−c 1
( )
Vemos que , ηB,t = 0 para λ=1 (no hay compresión) y también cuando
119
ηe σ =
λ
→ λ = ηeηcσ
ηc
Operando con T2 /T1 = T3 /T4 esta última expresión resulta en T3 -T4 = T2 -T1 , vale decir Lu=0, ηB,t =0
Dados ηc y ηe , para cada valor de λ (relación de compresión) existe un valor de σ (calor aportado) que maximiza el
trabajo útil. Haciendo dLu/dλ = 0 obtenemos
λ = ηeηcσ
(Lu =max)
Es también posible encontrar un valor de λ que maximiza η para cada σ, aunque su expresión no es explícita y se
obtiene de
λ2 (1 + σηc − σ ) + λ(− 2ηe σ ) + ηeηc σ 2 − ηeηcσ + ηeσ = 0
Como ejemplo, si ηe=ηc y ηe.ηc=0.7, los máximos y ceros de η son:
σ
2
3
4
λ (η=max)
1.216
1.6
1.92
λ (η=0)
1.4
2.1
2.8
ηmax
0.053
0.175
0.265
y su representación:
Fig. 9-7: Rendimiento del ciclo Brayton real
Se nota que, a diferencia del ciclo Brayton teórico, η aumenta con σ, aunque los rendimientos continúan siendo muy
bajos.
Luego, para obtener mejores rendimientos se debe aumentar σ (T3 , limitado por los materiales de la turbina) y utilizar el
λ (relación de compresión) óptimo.
4.
Ciclo de Brayton teórico regenerativo (o con recuperación de calor)
En este ciclo se aprovecha parte del calor de los gases de escape para precalentar el aire que entra a la cámara de
combustión, ahorrando parte del combustible.
El esquema de instalación y el diagrama del ciclo son:
120
Fig. 9-8: Ciclo Brayton con recuperación
Fig. 9-9: Diagrama i-s
Si el recuperador R fuera perfecto, T4 =T5 y T6 =T2 , y las áreas debajo (2-5) y (6-4) serían iguales
En este caso
Q1 = T3 − T5 , Q2 = T6 − T1
T2  P2 
Como
= 
T1  P1 
γ −1
γ
=
T3
T4
, también
T2 T6 T3
=
=
T1 T1 T5
Reemplazando y operando
ηB ,Rt =
Q1 − Q2
λ
= 1−
Q1
σ
Como no se alteran (T2 -T1 ) ni (T3 -T4 ), el trabajo útil es el mismo, sólo se reducen la entrega y cesión de calor (Q1 y
Q2 ), aumentando el rendimiento.
La figura muestra una instalación típica, con un recuperador de tubos (b) calentando el aire que sale del compresor (a) y
va a la cámara de combustión (c)
Fig. 9-10: Turbina a gas regenerativa (Vivier)
Se incluyen el alternador (e) y el motor de arranque (f)
El rendimiento del ciclo B.R. toma el valor 1-1/ σ para λ=1, y se anula para λ=σ. Cuando
valor que para el ciclo de Brayton simple:
λ = σ tiene el mismo
121
Fig. 9-11: rendimientos teóricos, BS y BR (Vivier)
Se aprecia que si λ > σ el B.S. tiene mayor rendimiento que el B.R.
De las igualdades T5 =T4 y T6 =T2 y de la adiabática
T2  p 2 
= 
T1  p1 
si T5 = T2 (luego T4 =T6 ) sale que
γ −1
γ
=
T3
T4
T2 T3
=
T1
T2
→ T2 = T1T3
λ= σ
Es decir, λ = σ identifica el caso en que T2 =T4 y no hay regeneración. Para λ > σ el BR funciona a la inversa,
el aire del compresor entrega calor a los gases de escape, reduciendo aún más el rendimiento:
122
Fig. 9-12: Ciclo Brayton regenerativo (Vivier)
En la figura, (F – G) identifica el caso límite T2 =T4 (Te),
La eficiencia del intercambiador es
ε=
λ= σ
(i 5 − i 2 ) ⋅ m& aire
(i 4 − i 6 )( m& aire + m& combust )
Si despreciamos la relación de masa combustible/aire (en las turbinas de gas, del orden de 0.02),
ε=
5.
T5 − T2
T4 − T2
Ciclo regenerativo real (ε
ε≠ 1)
En un caso real, T5 <T4’ y T6 >T2’ debido a ineficiencias del recuperador.
El trabajo útil será el mismo que para el ciclo Brayton simple real, ya que el recuperador sólo altera el flujo de calor:
λ
 λ − 1 
Lu = c p T1 
ηeσ − 
ηc 
 λ 
123
Fig. 9-13: Ciclo Brayton regenerativo real (Vivier)
Con la nomenclatura de la figura anterior:
ε=
i 2 − i1' T2 − T1'
=
ie' − i1' Te ' − T1'
Q = c p (Ta − T2 )
T − Te'
ηe = a
Ta − Te
λ = T1 / T0
σ = Ta / T0
De la primera
T2 = T1' + ε(Te' − T1' )
De la tercera
Te ' = Ta − ηe (Ta − Te )
Luego
Q = c p (Ta − T1 ' − εTe' + εT1' )
Operando, y reemplazando
ηc =
T1 − T0
T1 ' − T0


λ − 1
λ − 1 
 + εηc σ
Q = c p T0 (1 − ε )σ − 1 −

ηc 
 λ 


ηc σ − λ / ηc
λ−1
ηB , Rr =
⋅
λ


(σ − 1)(1 − ε ) + λ − 1 εσηc − (1 − ε ) λ 
λ 
ηc 
Si ε=0 obtenemos ηBS,r y si ε=1, ηBR,r
Si ηc=ηe=1 obtenemos
124
ηBR ,t (ε ≠ 1) =
(λ − 1)(σ − λ)
λ(σ − λ) + ε( λ2 − σ )
cuya gráfica es:
Fig. 9-14: Rendimientos ciclo Brayton regenerativo teórico, con regenerador de eficiencia variable (Vivier)
Se hace notar que para ε=0 se obtiene la gráfica de ηBS,t =1-1/ λ y no la indicada. Sin embargo, para ηc y ηe distintos de
1, la gráfica de ε=0 sí es la indicada en la figura.
6.
Ciclo Ericsson:
Este es un ciclo teórico, indicado en la figura:
Fig. 9-15: Ciclo Ericsson
La compresión 1-2 se efectúa a T=cte, por lo que es necesario enfriar (Qc ). Similarmente, la expansión en la turbina a
T=cte requiere calor (QT)
Los trabajos de turbina y compresor son:
Lc = RT1 ln p 2 p = c p T1 ln λ
1
LT = RT3 ln p3
= c p T3 ln λ
p4
p 
λ =  2 
 p1 
γ −1
γ
El calor entregado es
Q = Q1 + QT = c p (T3 − T1 ) + c p T3 ln λ
(T1 =T2 )
125
Luego, el rendimiento de ciclo Ericsson simple es:
η=
LT − Lc
=
Q1 + QT
ln λ
σ
1+
ln λ
σ −1
Notar que como λ ≥ 1 y σ ≥ 1, η ≤ 1
Este rendimiento es muy bajo salvo si σ ≅ 1 , λ ≅ 1 (Lu ≅ 0)
Si el ciclo se hace regenerativo de modo que Q1 =Q2 , el calor a entregar es sólo Q=LT , con lo que el rendimiento es
ηε ,r =
LT − Lc
L
T
= 1 − c = 1 − 1 = ηCarnot
LT
LT
T3
El ciclo Ericsson regenerativo tiene el máximo rendimiento pero es imposible de implementar en la práctica ya que las
evoluciones isotérmicas no son apropiadas para las turbomáquinas.
En su lugar se utiliza el ciclo Brayton con enfriamiento y recalentamiento intermedios (ciclo compound), de tipo
regenerativo.
7.
Ciclo Compound (Brayton regenerativo con enfriamiento y recalentamiento intermedios)
Este ciclo aproxima al ciclo Ericsson regenerativo utilizando enfriamiento y recalentamiento para asemejarse a las
isotermas. Es el ciclo utilizado en las instalaciones de mayor potencia, y puede realizarse en una sola máquina (un solo eje) o
en dos o más máquinas.
Una posible realización en dos ejes sería:
Fig. 9-16: Ciclo Compound
El diagrama real sería:
126
Fig. 9-17: Ciclo Compound real (Vivier)
8.
Combustión
Las turbinas de gas de uso aeronáutico utilizan combustibles líquidos similares al kerosene. La tabla siguiente ilustra
especificaciones y valores típicos:
127
Fig.9-18: Especificaciones de combustibles típicos (Hawthorne)
De estas especificaciones se pueden destacar:
128
a)
b)
c)
d)
El contenido de aromáticos (producen llamas largas y luminosas, indeseables en la turbina de gas)
El contenido de azufre (corrosión)
La curva de destilación, la viscosidad y la presión de vapor (controlan la atomización del combustible)
El poder calorífico y la densidad (cantidad de energía que cabe en los tanques del avión).
Las turbinas terrestres utilizan combustibles con especificaciones menos severas (dieseloils, gasoils, fueloils), excepto
por el control de azufre y de álcalis y metaloides como calcio, magnesio, sodio, vanadio.
Para uso continuado a altas potencias (grandes usinas) en nuestro país se utiliza mayoritariamente el gas natural
(metano)
La figura siguiente ilustra la estructura típica de una cámara de combustión:
Fig. 9-19: Cámara de combustión (Stevenazzi)
El aire comprimido proveniente del compresor ingresa por (1) en cantidades aproximadamente estequiométricas para
mezclarse con el combustible (2) y formar la llama. Aire secundario (4) completa la combustión de CO, etc. Parte del aire
restante circula entre el tubo de llama (8) y la caja de aire o carcasa (10), y refrigera el tubo de llama (5). Finalmente, el resto
del aire diluye y enfría los gases (6) a la temperatura aceptable a la entrada de la turbina (7)
Las cámaras de combustión pueden ser un número de recipientes cilíndricos, o bien un solo recipiente anular:
Fig. 9-20: Cámara anular (Mattaix)
129
La figura siguiente ilustra un inyector de combustible líquido típico:
Fig. 9-21: Inyector Duplex (G. Smith)
Algunos puntos a considerar en el tema de cámaras de cámaras de combustión son:
a) La relación aire/combustible global es mucho mayor que la estequiométrica, pudiendo alcanzar 50/1 y 70/1 (teórica, 1516/1). El aire resultante se utiliza para refrigerar y diluír.
b) La combustión es a presión constante. La pérdida de presión de estagnación en la cámara debe ser mínima para no perder
eficiencia.
c) La caja de aire soporta la presión, y el tubo de llama la aísla del calor por radiación y convección/conducción. El diseño de
los pasajes de refrigeración del tubo de llama es de importancia fundamental para su duración en servicio y baja pérdida de
presión de estagnación.
d) Las llamas largas, luminosas rápidamente destruyen el tubo de llama. Mala atomización del combustible es una causa
usual.
e) Se encuentra que el largo de la cámara es función inversa de la presión, y no depende de la potencia (temperatura), por lo
que las cámaras de las turbinas modernas (mayores presiones) son más cortas que las antiguas.
f) Las velocidades de aire a la entrada son muy bajas ( decenas de metros por segundo). A la salida, la expansión de los gases
puede llevarlas a velocidades sónicas o supersónicas.
130