UNIDAD

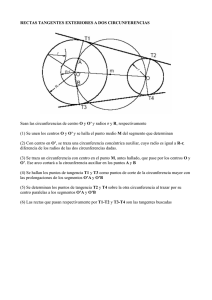
UNIDAD
4
Tangencias y enlaces
ÍNDICE DE CONTENIDOS
1. CONCEPTOS BÁSICOS SOBRE TANGENCIAS Y ENLACES . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.1. Relaciones entre rectas y circunferencias. Propiedades . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2. Lugares geométricos definidos por condiciones de tangencia . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.3. Enlaces . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2. TRAZADO DE RECTAS TANGENTES A CIRCUNFERENCIAS . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.1. Rectas tangentes a una circunferencia que pasan por un punto . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.2. Rectas tangentes a dos circunferencias . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3. TRAZADO DE CIRCUNFERENCIAS DE RADIO DADO TANGENTES A RECTAS, A OTRAS
CIRCUNFERENCIAS, O QUE PASAN POR PUNTOS . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.1. Circunferencia de radio dado que pasa por dos puntos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.2. Circunferencias de radio dado tangentes a una recta, y que pasan por un punto . . . . . . . . . . . . . . .
3.3. Circunferencias de radio dado tangentes a una circunferencia, y que pasan por un punto . . . . . . . .
3.4. Circunferencias de radio dado tangentes a una circunferencia y a una recta . . . . . . . . . . . . . . . . . . .
3.5. Circunferencias de radio dado tangentes a dos rectas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.6. Circunferencias de radio dado tangentes a dos circunferencias . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4. TRAZADO DE CIRCUNFERENCIAS TANGENTES A RECTAS, A OTRAS CIRCUNFERENCIAS,
O QUE PASAN POR PUNTOS . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.1. Circunferencia que pasa por tres puntos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.2. Circunferencia tangente a una recta que pasa por dos puntos, situado uno de ellos en la recta . . . .
4.3. Circunferencia tangente a otra circunferencia que pasa por dos puntos, situado uno de ellos en la circunferencia
4.4. Circunferencias tangentes a dos rectas que pasan por un punto situado en una de ellas . . . . . . . . .
4.5. Circunferencias tangentes a una recta y a otra circunferencia, que pasan por un punto situado en la circunferencia
4.6. Circunferencias tangentes a una recta y a otra circunferencia, que pasan por un punto situado en la recta
4.7. Circunferencias tangentes a otras dos circunferencias, que pasan por un punto situado en una de ellas .
4.8. Circunferencias tangentes a tres rectas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
En la tipografía, en el diseño, en la arquitectura,... se utilizan líneas compuestas por
segmentos y arcos de circunferencia enlazados, que presentan continuidad en su trazado. La tangencia posibilita el enlace.
El conocimiento de las construcciones de tangencia permite también resolver otros
problemas geométricos y trazar curvas técnicas como el óvalo, el ovoide, la voluta,...
En esta Unidad se estudia la construcción de rectas que cumplen dos condiciones
del tipo: pasar por un punto, ser tangentes a una circunferencia. O de circunferencias
que cumplen tres condiciones del tipo: tener radio dado, pasar por un punto, ser tangentes a una recta, ser tangentes a una circunferencia.
78
80
80
81
83
84
84
85
87
87
87
88
89
90
90
92
92
93
93
94
94
95
96
96
Se inicia la Unidad presentando las propiedades de la tangencia entre recta y circunferencia, o entre dos circunferencias y los lugares geométricos, que se utilizan para
determinar los centros de las circunferencias que cumplen dos condiciones.
Al desarrollar las construcciones, los centros de las circunferencias que cumplen
tres condiciones, se obtienen como intersección de dos lugares geométricos, que resultan de tomar las condiciones dos a dos. La solución puede ser múltiple, pues cada uno
de dichos lugares geométricos puede estar formado por dos o más líneas.
Estos son los contenidos esenciales de la Unidad:
T
Propiedades de las circunferencias tangentes a rectas y que pasan por puntos.
Condiciones de enlace de líneas.
T
Construcción de rectas tangentes que cumplen dos condiciones.
T
Construcción de circunferencias tangentes que cumplen tres condiciones.
T
Determinación dimensional de objetos.
Relaciones entre rectas y circunferencias
Pasar por un punto
Radio conocido
Ser tangente a una circunferencia
Ser tangente a una recta
Secantes
Tangentes
1ª Propiedad
2ª propiedad
Trazado de rectas que cumplen
dos condiciones
3ª propiedad
Trazado de circunferencias que
cumplen tres condiciones
79
UNIDAD
4
TANGENCIAS Y ENLACES
1. Conceptos básicos sobre
tangencias y enlaces
1.1. Relaciones entre rectas y circunferencias.
Propiedades
Una recta y una circunferencia, o dos circunferencias, se relacionan entre sí
atendiendo al número de puntos que comparten (Ilust. 1):
•
Secantes si tienen dos puntos comunes (puntos de corte).
•
Tangentes si tienen un único punto en común (punto de tangencia).
•
Exteriores si no tienen puntos comunes y en el caso de dos circunferencias, interiores cuando una encierre a la otra o concéntricas si comparten el mismo centro.
Exteriores
Secantes
Tangentes
Exteriores
Secantes
Tangentes
exteriores
Interiores
Concéntricas
Tangentes
interiores
Ilustración 1
En la Fig. a de la Ilust. 2 se puede ver que cuando una recta es secante a una
circunferencia, el triángulo OPQ es isósceles y la mediatriz de su base PQ pasa por
O. Se puede considerar la tangente s (Fig. b) como una secante en la cual P y Q
coinciden y al ser Ô = 0º serán P̂ = Q̂ = 90º. En consecuencia:
•
Primera propiedad: La mediatriz de una cuerda pasa por el centro de la circunferencia.
80
•
Segunda propiedad: La tangente a una circunferencia es perpendicular al
radio que pasa por el punto de tangencia.
En la Fig. c se ha trazado la secante s que pasa por los puntos comunes P y Q
de dos circunferencias secantes. Cuando la distancia entre los centros OO’= r + r’
(Fig. d), o OO’= r - r’ (Fig. e) los puntos P y Q coinciden y s es tangente a las dos circunferencias y por tanto perpendicular a sus radios OP y O’P. En consecuencia:
•
Tercera propiedad: Dos circunferencias tangentes tienen sus centros alineados con el punto de tangencia.
s
P
P=Q
r
r
O
α
O
Q
a)
s
c
b)
s
P
r
O
90º
s
90º
r’
r’
O’
P=Q
O’
r
r
90º
Q
r’
P=Q
O’
O
O
s
c)
d)
e)
Ilustración 2
1.2. Lugares geométricos definidos por
condiciones de tangencia
En la Ilust. 3 aparecen ejemplos de los lugares geométricos que se enuncian a
continuación y que se utilizan para realizar las construcciones de tangencia. En lo
sucesivo se identificarán en las construcciones por su número entre paréntesis.
(1) El lugar geométrico de los centros de las circunferencias de radio r que
pasan por un punto P es la circunferencia de centro P y radio r.
(2) El lugar geométrico de los centros de las circunferencias que pasan por
dos puntos P y Q es la mediatriz de PQ.
81
4
UNIDAD
TANGENCIAS Y ENLACES
(3) El lugar geométrico de los centros de las circunferencias tangentes a una
recta s en un punto T es la perpendicular a s en T. El lugar geométrico de
los centros de las circunferencias tangentes a otra circunferencia de centro O en un punto T es la recta OT.
(4) El lugar geométrico de los centros de las circunferencias de radio r tangentes a la recta s son las paralelas a s a la distancia r.
r
r
P
P
Q
T
s
O
(1)
(3)
(2)
s
r
r
r
r’
r
r - r’
(4)
O
r + r’
(7)
(6)
(5)
(6) y (7)
Ilustración 3
(5) El lugar geométrico de los centros de las circunferencias tangentes a dos
rectas dadas es la bisectriz del ángulo que forman.
(6) y (7) El lugar geométrico de los centros de las circunferencias de radio r’
tangentes exteriores (6) e interiores (7) a la circunferencia de centro O y
radio r son las circunferencias de centro O y radios r + r’ y r - r’.
82
1.3. Enlaces
En la Ilust. 4 arriba, se ha dibujado una curva indicando en ella los tipos de punto
más frecuentes:
•
Ordinario A: donde se dibuja la tangente t y la normal n.
•
Anguloso B: cuando en el punto B se pueden trazar dos tangentes diferentes t y t’ a cada una de las partes en que la curva queda dividida.
•
De inflexión C: cuando la tangente en C es única pero cambia la posición
del centro de curvatura antes y después de C.
t
n
t
t’
t t’
A
B
Anguloso
Ordinario
t
a
r’
Inflexión
t t’
P
t’
r
O
C
b
a
T
P
a
t
b
O
O’
s
O
O’
r
b
t’
Punto de unión
Punto de enlace
T
m
Punto de unión P
y de enlace T
Ilustración 4
Cuando se trata de enlazar un arco de circunferencia con otro, o con una semirrecta (Ilust. 4 abajo), puede hacerse mediante un punto anguloso (punto de unión),
pero es más característico utilizar un punto ordinario o de inflexión (punto de enlace).
Enlace es la unión de dos o más líneas curvas o rectas, de modo que aparentemente constituyan una sola.
83
4
UNIDAD
TANGENCIAS Y ENLACES
2. Trazado de rectas tangentes a
circunferencias
2.1. Rectas tangentes a una circunferencia
que pasan por un punto
P
P
O
O
t
Ilustración 5
Sea la circunferencia de centro O y P un punto de ella (Ilust. 5).
Se traza la recta OP y se levanta su perpendicular por P, que será la tangente t.
P
T
P
O
O1
O1
T’
Ilustración 6
Sea la circunferencia de centro O1 y el punto P exterior a ella (Ilust. 6).
Se traza el segmento O1P y su mediatriz, que lo corta en O. La circunferencia
de centro O y radio OP corta a la dada en los puntos de tangencia T y T’ por los que
trazaremos las tangentes PT y PT’.
El ángulo O1TP, inscrito en la circunferencia de centro O, mide 90º ya que su central correspondiente O1OP mide 180º.
84
2.2. Rectas tangentes a dos circunferencias
O2
r2
T’’
r1
O1
O2
A
r1 - r 2
r2
O
r1
T’’’
O1
r1 - r2
B
Ilustración 7
Sean las circunferencias de centros O1, O2 y radios r1, r2.
Si se desea trazar las tangentes exteriores comunes a ambas, reduciremos esta
construcción (Ilust. 7) a la anterior, restando el radio r2 de la circunferencia menor al
radio r1 de la mayor, que quedará convertida en la de centro O1 y radio r1 - r2 (línea
de trazos gruesos).
Determinaremos entonces los puntos de tangencia A y B de las tangentes trazadas desde O2 a la circunferencia de trazos gruesos.
Prolongando O1A, O1B para obtener T, T’ se trazan las soluciones TT’’, T’T’’’ paralelas a las rectas AO2 y BO2.
O2
r2
A
r1
O1
T’’’
O2
r2
O
r1 + r2
r1
T’’
O1
r1 + r2
B
Ilustración 8
85
4
UNIDAD
TANGENCIAS Y ENLACES
Si se desea trazar las tangentes interiores comunes a ambas (Ilust. 8) se procederá de manera análoga, trazando la circunferencia concéntrica con la mayor (línea de
trazos gruesos) de radio r1 + r2, siendo las tangentes solución paralelas a O2A y O2B.
Aplicación
En los dibujos técnicos de piezas industriales aparecen segmentos y arcos
cuyas longitudes, posición, centros y radios están definidas por las cotas y otras
líneas compuestas de segmentos y arcos enlazados, cuyos puntos de enlace y
centros deben ser determinados. Los centros de los arcos aparecen definidos
por el corte de ejes perpendiculares (líneas de rayas y puntos), que pueden ser,
además, de simetría de la pieza. Los puntos de enlace y los centros de arcos
enlazados se obtienen identificando y resolviendo un problema de tangencia.
12
33,3
10
26,6
COTAS EN MM
O2
O1
T’’
ESCALA 1:1
T’’’
Se desea reproducir el alzado de la leva cuyas dimensiones aparecen acotadas en el croquis. Se dibujan en primer lugar los tres ejes y las circunferencias
de radios 10 / 26,6 / y 12 mm.
La construcción de las rectas tangentes a las circunferencias de radios 12
mm y 26,6 mm, permite obtener los puntos de enlace T, T’, T’’, T’’’ y trazar TT’,
T’’T’’’.
86
3. Trazado de circunferencias de radio
dado tangentes a rectas, a otras circunferencias, o que pasan por puntos
3.1. Circunferencia de radio dado que pasa
por dos puntos
r
r
P
P
O’’
Q
O’
Q
Ilustración 9
Sea r el radio de la circunferencia y P, Q los puntos (Ilust. 9).
Los centros de las circunferencias solución están en las intersecciones de la
mediatriz de PQ con la circunferencia de centro P y radio r.
3.2. Circunferencias de radio dado tangentes
a una recta, y que pasan por un punto
Sea r el radio de la circunferencia, s la recta y P un punto de ella (Ilust.10
izquierda).
Los centros de las circunferencias solución están en las intersecciones de la perpendicular a la recta s en P con la circunferencia de centro P y radio r.
Si el punto P es exterior (Ilust. 10 derecha), los centros de las circunferencias
solución estarán en las intersecciones de la paralela a la recta s a la distancia r con
la circunferencia de centro P y radio r.
87
4
UNIDAD
TANGENCIAS Y ENLACES
r
r
P
s
s
P
s
r
r
O’’
O’’
P
r
P
s
O’
O’
Ilustración 10
3.3. Circunferencias de radio dado tangentes
a una circunferencia, y que pasan por un
punto
r
P
r1
P
r + r1
O1
O1
P
r1
r
O’’
r1
r - r1
O’’
O’’’
P
O’
O1
O’
Ilustración 11
88
r1
O1
O’’’’
Sea la circunferencia de centro O1 y radio r1, P un punto de ella, y r el radio de
las circunferencias tangentes (Ilust. 11 izquierda).
Los centros de las circunferencias solución están en las intersecciones de la
recta O1P con la circunferencia de centro P y radio r.
Si el punto P es exterior (Ilust. 11 derecha), los centros de las circunferencias
solución estarán en las intersecciones de la circunferencia de centro P y radio r con
las circunferencias de centro O1 y radios r + r1 y r - r1.
3.4. Circunferencias de radio dado tangentes
a una circunferencia y a una recta
r
r1
r + r1
O1
r - r1
s
r1
O’
O1
O’’
O’’
r
O’’’’
s
Ilustración 12
Sea la circunferencia de centro O1 y radio r1, s una recta, y r el radio de las circunferencias tangentes (Ilust. 12).
Los centros de las circunferencias solución están en las intersecciones de la
paralela a la recta s a la distancia r con las circunferencias de centro O1 y radios
r + r1 y r - r1.
89
UNIDAD
4
TANGENCIAS Y ENLACES
3.5. Circunferencias de radio dado tangentes
a dos rectas
r
a
b
a
O’’’’
O’
O’’’
O’’
b
r
Ilustración 13
Sea r el radio de la circunferencia y a, b las rectas (Ilust. 13).
Los centros de las circunferencias solución están en las intersecciones de la
paralela a la recta b a la distancia r con las bisectrices de los ángulos que forman las
rectas a, b.
3.6 Circunferencias de radio dado tangentes
a dos circunferencias
Sean las circunferencias de centros O1, O2 y radios r1, r2 y sea r el radio de las
circunferencias tangentes interiores y exteriores a ambas (Ilust. 14).
Los centros de las circunferencias solución están en las intersecciones de las circunferencias de centro O1 y radios r + r1 y r - r1 con las circunferencias de centro O2
y radios r + r2 y r - r2.
90
r
r + r1
r - r1
r + r2
r - r2
O’’’
r1
O1
O2
r2
O’’’’
O’
O’’
r1
O1
O2
r2
Q’’
Q’’’’
Q’
Q’’’
Ilustración 14
Existen ocho soluciones, de las cuales sólo se han dibujado las que tienen por
centro los puntos O’, O’’, O’’’, O’’’’, indicándose los centros Q’, Q’’, Q’’’, Q’’’’ de las
otras cuatro.
Aplicación
COTAS EN M
P
desea trazar una carretera de acceso formada por
5
13
33
En una parcela se ha construido un edificio y se
O1
arcos de circunferencia de centro O1 y radio 33 m, tramos rectos de entrada y salida paralelos a las lindes,
rotonda para aparcamiento de radio 5 m, y dos desvíos
de enlace de radio 13 m, que deben pasar por P.
Situados P y O1 sobre el plano, se traza la circunfe-
rencia de centro O1 y radio 33 m y las circunferencias de radio 13 m, tangentes
interiormente a ella que pasan por P. Sus centros O’, O’’ están en las intersecciones de la circunferencia de centro P y radio 13 m (lugar geométrico 1) con la circunferencia de centro O1 y radios 33 - 13 m (lugar geométrico 7).
91
4
UNIDAD
TANGENCIAS Y ENLACES
Los puntos de enlace T’’, T’’’
(1)
se obtienen alineados con los
T’’’
T’’
T
P
centros de las circunferencias
tangentes (rectas O1O’ y O1O’’).
T’
O’’
O’
(6)
(6)
(6)
T’’’’
T’’’’’
O1
La rotonda será la circunferencia de radio 5 m, tangente
interior a las de radio 13 m y centros O’, O’’ (lugar geométrico 6).
Las perpendiculares a las lindes desde O1 nos dan los puntos
de enlace T’’’’, T’’’’’ con los accesos de entrada y salida, que
serán las tangentes a la circunfe-
rencia de centro O1 en dichos puntos.
4. Trazado de circunferencias tangentes
a rectas, a otras circunferencias, o que
pasan por puntos
4.1. Circunferencia que pasa por tres puntos
C
C
A
A
B
O’
B
Ilustración 15
Sean A, B, C los tres puntos (Ilust. 15).
El centro de la circunferencia solución está en la intersección de las mediatrices
de AB y BC .
92
4.2. Circunferencia tangente a una recta
que pasa por dos puntos, situado uno de
ellos en la recta
s
s
O’
A
A
B
B
Ilustración 16
Sea s la recta, A un punto de ella y B un punto exterior (Ilust. 16).
El centro de la circunferencia solución está en la intersección de la perpendicular a la recta s en A con la mediatriz de AB .
4.3. Circunferencia tangente a otra circunferencia
que pasa por dos puntos, situado uno de ellos en
la circunferencia
A
A
O1
B
O1
O’
B
Ilustración 17
Sea la circunferencia de centro O1, A un punto de ella y B un punto exterior (Ilust. 17).
Los centros de las circunferencias solución están en las intersecciones de la
recta O1A con la mediatriz de AB .
93
4
UNIDAD
TANGENCIAS Y ENLACES
4.4. Circunferencias tangentes a dos rectas
que pasan por un punto situado en una de ellas
b
b
O’’
A
A
O’
a
a
Ilustración 18
Sean a, b las rectas y A un punto de la recta b (Ilust. 18).
Los centros de las circunferencias solución están en las intersecciones de la perpendicular a la recta b en A con las bisectrices de los ángulos que forman las rectas
a y b.
4.5. Circunferencias tangentes a una recta
y a otra circunferencia, que pasan por un
punto situado en la circunferencia
t
O1
r1
A
O’
O1 r 1
A
O’’
a
a
Ilustración 19
94
Sea la circunferencia de centro O1, A un punto de ella y a la recta (Ilust. 19).
Se construye la tangente t a la circunferencia en el punto A.
Los centros de las circunferencias solución están en las intersecciones de la
recta O1A con las bisectrices de los ángulos que forman las rectas a y t.
4.6. Circunferencias tangentes a una recta
y a otra circunferencia, que pasan por un
punto situado en la recta
c’’
r1
O1
c’
O’’
A’’
v’
v’’
O’
a
A
A’
O1
O1
r1
O’’
A’’
r1
O’
a
A
a
A’
A
Ilustración 20
Sea la circunferencia de centro O1 y radio r1, a una recta, y A un punto de ella
(Ilust. 20).
Los centros de las circunferencias solución están en las intersecciones de la perpendicular a la recta a en A con las mediatrices de A ' O1 y A ' ' O1 .
En la figura de análisis puede verse que las soluciones v’, v’’ son concéntricas con
las circunferencias c’, c’’. Al trazar los segmentos AA ' = AA ' ' = r1 reducimos la construcción a la de obtener, sobre la perpendicular a la recta a por A, los centros O’, O’’
de las circunferencias que pasan por los puntos O1, A’ y O1, A’’ respectivamente.
95
4
UNIDAD
TANGENCIAS Y ENLACES
4.7. Circunferencias tangentes a otras dos
circunferencias, que pasan por un punto
situado en una de ellas
A’’
O2 r
2
r1
O1
A
O’’
A’’
A’
O2 r2
r1
O1
A
O’
A’
Ilustración 21
Sean las circunferencias de centros O1, O2 y radios r1, r2 y A un punto de la segunda.
En la (Ilust. 21), sobre los datos, se han dibujado los puntos A’, A’’ situados en la
recta O2 A, a las distancias AA ' = AA ' ' = r1 .
Los centros de las circunferencias solución están en las intersecciones de la
recta O2 A con las mediatrices de A ' O1 y A ' ' O1 .
La construcción se reduce a la de obtener, sobre la recta O2A, los centros O’, O’’
de las circunferencias concéntricas con la solución, que pasan por los puntos O1, A’
y O1, A’’ respectivamente.
4.8. Circunferencias tangentes a tres rectas
Sean a, b, c las tres rectas (Ilust. 22).
Los centros de las circunferencias solución están en las intersecciones de las
bisectrices de los ángulos que forman las rectas.
96
O’’
a
b
O’’’
c
O’’’’
Ilustración 22
Recuerda
T
La mediatriz de una cuerda pasa por el centro de la circunferencia.
T
La tangente a una circunferencia es perpendicular al radio que pasa por el punto
de tangencia.
T
Dos circunferencias tangentes tienen sus centros alineados con el punto de tangencia.
T
Para dibujar una pieza, primero se trazan los ejes y las líneas cuyas dimensiones
estén definidas, después se identifican y resuelven las construcciones de tangencia que permiten obtener los centros y puntos de enlace de segmentos o arcos.
97
UNIDAD
4
TANGENCIAS Y ENLACES
Actividades
1. Dibujar el contorno del hueco de
la letra D, según se indica en el
croquis, a escala natural.
13
39
26
COTAS EN MM
2. Trazar las circunferencias tangentes a la de centro O1 y radio r1
en el punto A y a la recta r.
3.
A
O1
r
La gola es una moldura formada
por una doble curva, con la parte
superior cóncava y la inferior convexa. Enlazar los puntos A y B
mediante una gola según el croquis.
A
B
r
A
14,5 mm
B
s
COTAS EN MM
5,45
6,3
4. Representar la arandela a escala
10:1. Al ser simétrica es suficiente dibujar la mitad.
4,32
30º
1,05
0,7
8,24
98