Bipolares
Anuncio

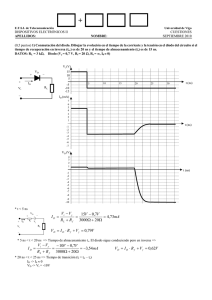
PROBLEMA 2 Sea el amplificador multietapa de la figura, se pide: • El punto de trabajo de cada transistor • Las ganancias Av,Ai y Ap • Las impedancias de entrada Zi y salida Zo • La frecuencia de corte que impone cada condensador y la consecuencia, la frecuencia de corte inferior del amplificador. Solución al apartado a): En primer lugar calcularemos el punto de trabajo de cada transistor, lo haremos sobre el circuito en continua, por lo que consideraremos en cto abierto y no lo hace falta que lo pasemos a señales. El punto de trabajo del primer transistor es: Q(9,82V, 1,05mA) En la segunda parte del circuito veremos que sera muy similar, ya que lo unico que cambia, es la Rc2 El punto de trabajo del segundo transistor es: Q(7,93V, 1,05mA) Solución al apartado b): Para realizar los cálculos que se piden, consideraremos el circuito equivalente para pequeña señal. Como se nos relacionan la ib1 e ib2, buscaremos una ecuacion que nos relacione ambas, para eso iremos a la parte central del circuito en señales. 1 Solución al apartado C): Solución al apartado D): La frecuencia sabemos que viene delimitada por los efectos capacitivos. Siendo Requ en cada caso la que ve el condensador. En el caso de Cgen En el caso de C12 En el caso de Cl 2 En el caso de Ce como el valor del condensador tiende a infinito el de la frecuencia de corte tendera a cero. ib2 R11 Re1 Rc1 C12 Cgen Vcc Re2 Rc2 Vgen VCC R21 Q1 R22 Q2 Vgen ib1 Hie Rb1 Rb21e2 Rc2 RC2 Hie V0 3 + − Rc1 ib2 ib2 Ri B1 C1=B2 E2 C2 Ro V0 − + Rb21e2 ib1 Hie RC2 ib1 Rc2 ib1 B1 ib2 Rb1 4 Vgen Ro ib1 E1 Ce1 Ri C!" Cgen 5 Rc1 ib1 E1 Cgen Rc1 ib1 E1 Vi Cl R12 ib1 Rc2 ib1 + V0 − B1 ib2 ib2 V0 − + Rb21e2 6 Hie RC2 Rb1 Vgen Ro Ri Ri Ro Vgen Rb1 RC2 Hie Rb21e2 + − V0 ib2 ib2 B1 ib1 Rc2 7 ib1 E1 ib1 Rc1 Cl 8