Test de habilidades para resolver problemas matemáticos. (Charla

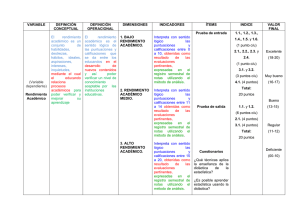
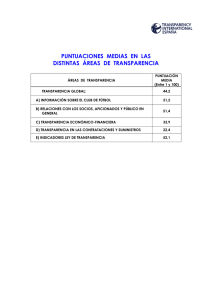
Test de habilidades para resolver problemas matemáticos. (Charla corta)
Mario Orlando
[email protected]
Universidad de San Andrés
25 de Mayo 586 (C1002ABL) Ciudad de Buenos Aires
Tel: (54-11) 4312-9499 - [email protected]
Resumen
El trabajo analiza las habilidades cognitivas implicadas en la resolución de problemas matemáticos y su incidencia en el rendimiento escolar, desde la perspectiva de la teoría triáquica de la
inteligencia de R. Sternberg. La metodología está basada en la administración de dos instrumentos validados en un estudio previo mediante el análisis estadístico y el juicio experto, que posibilitan identificar distintos niveles de habilidad en los alumnos. Uno de ellos facilita la evaluación
dinámica del desempeño a través del empleo de TIC y funda la indagación en ítems liberados de
la prueba PISA; el otro instrumento constituye una adaptación local del SAT (Sternberg Triarchic
Abilities Test). La población examinada abarcó 419 alumnos ingresantes a la carrera “Despachante de Aduanas”, de la Ciudad de Buenos Aires. Los resultados obtenidos valoran dominios de
habilidad vinculados con la comprensión lingüístico-semántica, el conocimiento esquemático, el
estratégico, la ejecución algorítmica y el tratamiento y puesta en práctica de nueva información. La experiencia recogida contribuye a incrementar la objetividad en la evaluación de
competencias predictoras del rendimiento escolar y mejorar las propuestas de exámenes de
selección para ingresar a estudios de nivel superior.
Palabras clave: Simulación digitalizada, Resolución de problemas, rendimiento escolar. I. Introducción
La competencia en matemática es un requerimiento básico para un efectivo desempeño ciudadano en una sociedad moderna. Entre las competencias que contribuyen a un desempeño competente en la construcción social e interpretación de objetos reales y simbólicos, se ha señalado la
capacidad de resolver problemas matemáticos. Este trabajo identifica habilidades cognitivas que
actúen como estimadores confiables de tales capacidades. El interés se centra en determinar la
mejor aproximación posible a la probabilidad de éxito escolar a partir de las calificaciones obtenidas en test de habilidades para resolver problemas Matemáticos y las puntuaciones del STAT
(Sternberg Triarchic Abilities Test), más allá de demostrar su grado de correlación.
En Buenos Aires, la demanda por algunas carreras de educación superior supera considerablemente la oferta, situación que determinó que el Instituto de Formación Técnica Superior Nº6 haya
decidido identificar las competencias consideradas básicas para mejorar el rendimiento en las
materias troncales de la carrera “Despachante de Aduanas” y a los aspirantes que tengan mayor
probabilidad de éxito de concluir los estudios, a partir del principio de mérito y a través de
mecanismos objetivos. Se diseñó y aplicó a 419 alumnos un test matemático online que posibilitó
ordenar a los ingresantes en el ciclo 2011, de acuerdo con el nivel de desarrollo de las habilidades
cognitivas identificadas como relevantes. Se analizó la relación de las habilidades cognitivas con
el nivel de desarrollo de las competencias: lingüístico-semántica, para identificar la naturaleza del
problema, para elegir un plan de resolución, para seleccionar estrategias, para la ejecución correcta de algoritmos matemáticos y para adquirir nueva información o recordar la existente. Se
aplicó la teoría triárquica de la inteligencia, porque hace posible concebir operaciones de medición
que permiten evaluar las capacidades postuladas por la teoría de manera confiable y válida.
Las teorías cognitivas han formulado modelos explicativos de los factores que intervienen en el
desarrollo de las habilidades para resolver problemas. Los estudios orientados a identificar aquellas habilidades específicas de dominio asociadas a la experticia, muestran que el éxito o el fracaso para resolver problemas se puede explicar en parte acudiendo a diferencias individuales en
inteligencia general y en aptitudes intelectuales específicas. La mayoría de las investigaciones
publicadas en las últimas décadas reportan asociaciones significativas entre experticia en un
dominio y factores de inteligencia (Castejón Costa y Navas,1992; Castejón, J. 1996, Castejón
Costa y Miñano,2008; Pardo Merino y Olea Díaz, 1993; Alvaro Page et al., 1998; Bernad, 2000.
Es posible afirmar que detrás de la calificación obtenida través de una prueba o test de razonamiento matemático, se encuentra el supuesto, de que los sujetos con mayores puntajes tendrán
mayor probabilidad de éxito como estudiantes (Coll, 2004). La Inteligencia y la aptitud son las
variables que con mayor frecuencia son usadas como predictoras del rendimiento escolar, ya que
todo aprendizaje exige la puesta en práctica de procesos cognitivos; la mayor validez predictiva de
un instrumento que pone en práctica procesos cognitivos es conducente a la mayor probabilidad
de un mejor rendimiento académico.
II. Metodología
Enfocar la atención en la resolución de problemas, requiere la selección de aquellos que permiten
poner en evidencia los procesos y competencias cognitivas asociadas al dominio. En este sentido,
la competencia matemática evaluada por el proyecto PISA, cumple con dicha finalidad ya que uno
de sus objetivos es determinar en qué medida los jóvenes han adquirido los conocimientos y
habilidades matemáticas que les permitirá desenvolverse en la vida adulta. En consecuencia, se
seleccionaron quince 15 problemas que conformaron los ítems del Test de Habilidades para relevar el papel que desempeñan las variables: comprensión lingüístico-semántica, conocimiento
esquemático, conocimiento estratégico y ejecución algorítmica; esta última asociada con la habilidad para asimilar nueva información y ponerla en práctica. Cada ítem tiene cuatro (4) niveles de
respuestas de acuerdo con los componentes cognitivos involucrados. Las puntuaciones obtenidas se ordenaron de menor a mayor y se las dividió en tercios, para conformar el Grupo Superior,
el medio y el inferior. Estos datos se complementaron con las puntuaciones, en términos de
porcentaje, de las tres calificaciones básicas del STAT: Analítico, Práctico y Creativo; Igual criterio
utilizó para determinar las categorías Bajo, Regular y Alto establecidas como escala de estos
resultados.
Los test considerados posibilitan evaluar el desarrollo de habilidades cognitivas asociadas al
rendimiento escolar, teniendo en cuenta las categorías consideradas, en tanto que los coeficientes de correlación ofrecen una medida de la asociación lineal entre las variables estudiadas.
III. Resultados
La comparación de los procesos básicos involucrados en la resolución de problemas, evidencia
la existencia de un 23 % de alumnos que, con pobre conocimiento esquemático y estratégico, han
podido realizar cálculos algorítmicos y resolver los problemas; se han podido observar leves
diferencias entre las puntuaciones obtenidas en Ejecución Algorítmica con respecto a los otros
procesos evaluados; los bajos índices de acierto en los problemas: 4,8,10, y 15 refleja que el
45% de los alumnos no sabe ejecutar los procedimientos aleatorios que exigen estos problemas.
También muestra que el 40% que ejecutaron los algoritmos, no domina el conocimiento esquemático y estratégico que fundamenta el cálculo.
El rendimiento en el Test de habilidades para resolver problemas matemáticos en relación con los
valores extremos de las variables habilidad Analítica, Práctica y Creativa definidos por el STAT,
revelan como tendencia que las puntuaciones bajas en todas las habilidades consideradas, se
corresponden con una probabilidad de un bajo perfil de rendimiento escolar; el 34% de quienes
obtienen bajas calificaciones en las habilidades relevadas en el STAT obtienen una puntuación
general baja en el test de matemática y se podría asociar a un bajo perfil de rendimiento escolar.
Por el contrario, cuando las puntuaciones son altas, la mayor probabilidad no se traslada
necesariamente hacia calificaciones altas en las categorías del STAT, y en consecuencia a un
perfil alto de rendimiento escolar caracterizado por puntuaciones altas en las categorías de los
dos test. No obstante, al considera únicamente la variable de Habilidad Analítica, el 65% de los
alumnos con alta puntuación, también presentan un buen desempeño en la evaluación de
matemática.
Los datos indican que al adicionar las variables: Habilidad Analítica, Práctica y Creativa que determina el STAT a las puntuaciones obtenidas en el test de habilidades para resolver problemas
matemáticos, las probabilidades de rendimiento escolar mejoran.
Se puede observar que de los 253 estudiantes que tienen calificaciones bajas en el test matemático y una puntuación alta en alguna de las tres escalas del STAT, sólo 32 (9%) ha obtenido un
buen rendimiento en aplicar estrategias de adquisición de conocimiento para resolver problemas
sin disponer de un plan previo de resolución y, por lo tanto, en problemas caracteriza dos por un
cierto grado de dificultad. En tanto, la inmensa mayoría no ha logrado realizar los algoritmos necesarios para resolver los problemas planteados.
IV. Conclusiones
Los datos aportan algunas conclusiones relevantes que evidenciar la conveniencia de construir
instrumentos de evaluación teniendo en cuenta indicadores que permiten predecir el rendimiento y
las trayectorias que despliegan los estudiantes. La consideración de las habilidades intelectuales
definidas por ambos test como variables discretas permite analizar los datos relevados, a partir de
probabilidad condicional. Los resultados suponen que los procesos explorados en el test de
habilidades para resolver problemas matemáticos, posibilitan datos para un cálculo de
probabilidad del rendimiento escolar. En consecuencia, es conveniente otorgar a los procesos de
comprensión lingüístico-semántica y Ejecución Algorítmica mayor peso en las evaluaciones de
rendimiento.
Estos datos muestran una clara tendencia de asociación entre las calificaciones obtenidas en el
test de habilidades para resolver problemas y las puntuaciones de las tres calificaciones básicas
del STAT, que pueden funcionar como indicadores de aproximación al grado de predicción del
rendimiento escolar. Esto es, porque el rendimiento escolar se asocia a diversas variables o
características de los estudiantes lo que, a su vez, torna la problemática de la validez predictiva de
una gran complejidad.
El análisis indica que al considerar la variable Habilidad Analítica, las puntuaciones altas se
corresponden con una mayor probabilidad de obtener un perfil alto en el test de matemática y se
reduce al considerar los estudiantes de baja puntuación. En base a esto es factible decir que el
nivel de desarrollo de la Habilidad Analítica tiene una marcada incidencia en la capacidad de los
estudiantes para resolver problemas matemáticos. No caben dudas que el grado de asociación
medido a través de la probabilidad condicional ofrece una aproximación; sin embargo, habrá que
atender a algunas cuestiones que surgen del análisis. En primer lugar, explicar por qué 35% de
los estudiantes de altas calificaciones en STAT se caracteriza por un bajo rendimiento en el test
de habilidades para resolver problemas matemáticos. En segundo lugar, la proporción del 23% de
los estudiantes con calificaciones bajas en alguna de las escalas del STAT que se caracteriza por
puntuaciones altas en el test de habilidades para resolver problemas matemáticos.
En consecuencia, se podría sostener que la validez predictiva de los exámenes deberán tener en
cuenta el grado de desarrollo de habilidades cognitivas y habilidades para resolver problemas.
Por último, se puede destacar que los dos Test aplicados permiten un cierto grado de predicción
del rendimiento académico. Ello indica que se debe realizar un seguimiento del rendimiento
académico de los alumnos con la finalidad de ajustar los instrumentos que permitan lograr una
mayor precisión en su validez predictiva.
V. Bibliografía
• Alvaro Page et al. (1990). Hacia un modelo causal del rendimiento académico. Madrid : Centro
de Publicaciones del Ministerio de Educación y Ciencia.
• Beltran, J. (Coord.) (1991). I Seminario internacional sobre la mejora de la inteligencia: La inteligencia práctica en la escuela. Universidad de Murcia y U. Complutense de Madrid: ICE.
• Bernard Mainar, J, A. (2000). Modelo cognitivo de evaluación educativa. ESEAC - Escala de
Estrategias de aprendizaje Contextualizado. Madrid: Narcea, 2000, 201 pp. ISBN: 84-2771322-3.
• Castejon Costa, J.L., Miñano Pérez, P. (2008). Predicción del rendimiento escolar de los
alumnos a partir de las aptitudes, el autoconcepto académico y las atribuciones causales .
Revista Horizontes Educacionales Vol. 13, Núm.2 pp 11-23. Universidad del Bio Bio. Chile.
• Castejon Costa, J.L. y Navas, L. (1992). Determinantes del rendimiento académico en la
enseñanza secundaria. Un modelo causal. Análisis y Modificación de Conducta, 18 (61), 697730.
• Castejon Costa, J.L. (1996). Determinantes del rendimiento académico de los estudiantes y de
los centros educativos. Modelos y factores. Alicante: ediciones Club Universitario.
• Chain R., Cruz Ramirez, N., Martínez Morales, M. y Jácome, N. (2003). Examen de selección y
probabilidades de éxito escolar en estudios superiores. Estudio en una universidad pública
•
•
•
•
•
•
•
estatal mexicana. Revista Electrónica de Investigación Educativa, 5 (1). Consultado el
15/12/2010 en: http://redie.uabc.mx/vol5no1/contenido-chain.html
Coll, C. (2004). Psicología de la educación y prácticas educativas mediadas por las tecnologías
de la información y la comunicación. Sinéctica , 25 , 1-24.
Malbrán, M; Pérez, V. (2004). Potencialidad Educativa de la Simulación mediada por
Ordenadores. X Congreso Argentino de Computación. CACIC 2004. San Justo, La Matanza.
Pardo, A. y Olea, J. (1993). Desarrollo cognitivo-motivacional y rendimiento académico en
segunda etapa de E.G.B. y B.U.P. Estudios de Psicología, 49, 21-32.
Schoenfeld, A.H. (1982). Measures of problem-solving performance and of problem-solving
instruction. Journal for research in mathematics education, 13, 1, 31-39.
Sternberg, R. J.(1986) Introducción. ¿Cómo es el enfoque del procesamiento de la información
en las capacidades humanas?. En: Sternberg, R. op. Cit
Sternberg, R.J. (1985). Triarchic theory of human intelligence. Nueva York. Cambrige Universit.
Sternberg, R. J. (1987). Inteligencia Humana. Buenos. Aires: Paidós, tomo 1.