~ Existe un cambio brusco en la absorbancia para todas las plantas

7
~ Existe un cambio brusco en la absorbancia para todas las plantas en
\
.la vecindad de 0.7 a 1.5 micras o 14.800 CM- l , lo cual es explicable
en términos de la absorción del pigmento y el agua.
absorbe
fue~temente
1ilS
~ofila
en el azul y el roj o, mientra s que el vapor de
agua 10 hace en el infrarrojo lejano.
de
La c-
Este caracter espectra- Gnico
hojas, permite entonces abso rber efic i lü eme nte long' tudes de
onda del az ul y e roja los cua l es son requeridos para el
' oceso de
fotos ;'ntes i s.
Basado en la respuesta fisiológica de las plantas a, la radiación inci­
dente, Gates (1965), presenta un resumen de las divisiones del espec­
tro solar, como se indica en la Figura 5 (ver también Blackwell, 1966):
Primera banda:
Mayor de 1.000 micras .
ficos de esta radiación .
No se conocen efectos. espec.í.­
Se acepta que esta radiación es absorbida
por la planta y es transformada encalar sin interferir en los proce­
sos bioquímicos.
Segunda banda:
1.000 a 0. 7 micras.
Esta es la región de efectos pro­
longados especffica de la radiación en las plantas.
Tercera banda:
0.70 a 0.61 micras.
Esta es la región de más alto
nivel de absorción de clorofila y de más fuerte actividad fotosinté­
tica en la región del rojo.
) dad fotoperiódica más fuerte.
En muchos casos ella presenta la activi­
8
C-O
IN
DlSSOOACION
~
~:r2
~ZONO
BSORCION
EMPIEZA
~
~
-o-H
-C-H
\
~.~--~~~~~~~~~--~~~-T
1St
ULTRAVIOLE
C
8ci
B
A
7_
I
0280
FRA
ISI
. I±IJ
~ ~~~
AZUL
!S ti -
S ­a .
~
Q31!5
0.4000
0..510 0.610070
Q92 L\2
Va : VIII
1.<40 L90
ro
l ,...
lE
u
.....
'e~
"iE
(,)
-l
10(lO-5¡
f
r
<t
I
U
r
<t
U
Z
<t
O
<t
Ir
o:
LUZ SOLARDIRECTA
NIVEL DEL MAR
L34 Cm- 2 ...in .. 1
~4 %~-.t+_- J--4
~
35,000
'&l,OOO
25pOO
20,CXX>
NUMERO DE ONDAS Cm- I
1
025
I
Q3
1
I
04
Q5
I
0.6
\
I
I
I
I 11 1I
07 0 .9 OS 10
1
15 2P
1 IlIlftl
lro
40 100
LONGITUD DE ONDAS,MICRAS
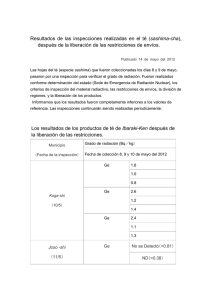
FIGURA 5. Distribución espectral de la radiación solar mostrando los
segmentos del espectro para consideración de los procesos
de las plantas. El contenido de quantum de cada frecuencia
de la radiación incidente se muestra en la escala marcada
en Kcal. (Adaptada de Gates, 1965).
Cuarta banda:
0.61 a 0.51 micras.
Esta es la región espectral de
más baja eficiencia fotosintética en el verde y de actividad forma­
tiva débil.
9
Quinta banda:
0.51 a 0.40 micras.
Esta es virtualmente la región de
absorción de clorofila en nivel alto y absorci6n por los pigmentos ama­
rillos.
Es también la región de fuerte actividad fotosint§tica en el
azul violeta y de fuertes efec t os formativos.
La región ul travioleta se puede div i dir por conv2n ienci a en los seg­
mentos A,
B~
C, basados más que t odo en efectos diferentes a los de
las reacciones de la planta.
A: 0.~'5
- 0.4 micras.
Produce fluorocencia en las plantas y fuerte
respuesta por las emulsiones fotográficas.
B: 0. 28 - 0.315 micras . Se pre senta significativa acción germicida.
c: Longitudes de onda más corta que 0.28 micras.
No alcanza la su­
perficie de la tierra, pero se utilizan para lámparas ultravio­
letas.
Por debajo de 0.16 micras se presentan efectos l etales
en algunas plantas.
1.3 UNIDADES DE RADIACION y TERMINOl OGIA.
Ex i ste confusi6n en la literatura, para mencionar las unidades utili­
zadas en radiación solar y en la terminologfa que se utiliza.
Irradiación:
expresa la tasa a la cual la energfa radiante es reci­
bida por una superficie.
Las unidades ut i 1 -izadas so n :
-2 s -1
W m-2 Joule:
~~att
J
:
m
Watt equivale a un Jo ul: s - 1
Langley:
Ly
. -1
m,n
,.
Caloría :
Cal cm
- t:.
min 1
Langley equivale a una C 1 cm -2
-2 . -1
.-1
Una Cal . cm m,n
equival e a 4,1855 J cm -2 m,n
Una Cal .
cm- 2 min- 1 eq uival e a 697,58 Wm- 2
Densidad de flujo: en á')se r.cia de una superficie, como en los flujos
sobre la veg etación s e ha
~ a.
de "densidad de flujo" de la energía ra- .
.. -2
diante y se util iza la uHi dad w m .
Unidades
Fotom~tricas:
en estudios de procesos fisiológicos, es más
apropiado utilizar unid aaes fotométricas, en las cuales la unid ) d fun­
damental es el "photón!! rn- 2 $-1 o I1quantum!l. Un Einstein ( E)
-2
m
$
-1
?3
equivale a 6.02 x 10- quantulO .
Para medir la Radiaciór Fotosintéticarnente Activa (RF,l'\), 400-750}tm,
se usa también el
. en el rango
"mc ~ " m- 2 s-\ ordinariamente 1a luz visible cae
-2
O - 2.000 me l m
s
-1
.
11 Con frecuencia, la radiación incidente sobre vegetación se mide en
unidades de iluminación (respuesta visual a la radiación) o sea:
"Candela - pié" o "l umen _ft 211 o IIluxes".
La unidad de flujo
1 1 ux =
°
lum~noso
1umen cm -2 .
es:
-2
1 1 umen m
1 candela-pie
=
10 . 76 lux
1.4 BALANCE DE ENERGIA Y RADIACION NETA.
Para comprender los mecanismos
te recibida en la superficie
de transfarmac o
íón
d~
la tierra se estableció la Ecuación
del Balance de Energía para una superficie con
con 1a termi no 1 ogía pro pues ta
de la energía radian­
PO}"
Freyoe
~!
( 1 - a - f ) RG - RB - El - Q - K
0­
vegetación~
de acuerdo
al (1975):
O
(1)
Los términos significan lo siguiente:
RG: Radiación Global.
Radiación de corta lcngitud de onda (0 . 3 ­
4.0 micras) recibida del sol (radiación directa) y del cielo
(radiación difusa) en la superficie horizontal de la tierra.
a
Representa el "al bedo", es decir, la fracción de energía de
corta longitud de onda reflejadd por el suelo o una superficie
cualquiera hacia el cielo .
Este factor 05cila de 0.05 en las
aguas libres y de 0.5 - 0.30 en suelos cubiertos por vegetación.
12 f
Representa la parte de radiación absorbida por la vegetación
vet'de y utilizada en fotosíntesis.
Su valor no es mayor general­
mente del 2% en condiciones naturales.
RB: Representa la radiación de onda larga resultante ( 4 - 50 micras)
procedente de la tierra y es el res ultado de los intercambios
de radiación
de onda larga que se producen entro la superficie
,
del suelo y la atmósfera.
ET: Representa el calor latente de evaporación.
Q
Conducción de calor; corresponde al calor transmitido
de~de
la
superficie del suelo hasta el subsu elo por conducci6n .
K
Convección; representa la parte de energfa solar recibida en la
superficie del suelo e intercambiada con la atmósfera por IIDifu­
sión turbulenta", llama do tainbién "Calor sensible".
1.4.1
Radiación Global.
La radiación s01ar global sufre en la atmósfera fenómenos de reriexión,
difusión y absorci6n (ver Figura 1).
La parte de radiación que llega
a la superficie s 'in estar afectada por los fenómenos mencionados se
denomina Radiación Directa (Rb); la otra parte llega a la superficie
en forma de radiación difusa (Rd).
13 J
El término Rb está muy influenciado por' las caractedsticas topográ­
/
)
ficas de la superficie (declive, exposici6n,
etc.)~
mientras que el
término Rd está menos afectado.
la radiaci6n global es parcialmente reflejada por la superficie, y
está dada por
11 ,
RG", donde "a" representa el albedo, o sea la cap()­
cidad de reflexi6n de radiaci6n solar incidente.
En la Tabla 1 se pueden observar los rangos de albedo,selectivospara
diferentes tipos de superficie, segan Satterlund, 1972, citado por
Lima (1985).
TABLA L Rango de albedos Ha H para diferentes superficies, según
Satterlund, 1972 (adaptada por Lima, 1986).
- - - -._- - - - - - - - - - - _._ - - -- - - - - - SuperFicie
Albedo (%) Agua
5 - 10
20 - 10
Suelo desnudo (seco~ claro)
Suelo desnudo (húmedo, oscuro)
8 - 15
?r:: _
.35
Pasto (bajo, verde, no mojado)
15 - 20
Pasto (bajo. verde, moja~o)
Pasto (alto, verde)
15 - 20
15 - 20
Pantarlo
5 - 10
Bosque de coníferas
Bosque mixto de coníferas y especies hoja ancha 10 15
15 - 20
Bosque de especies de hoja ancha
Bosque tropical
15
20
Bosque de eucalipto
80 - 95
Nieve
~"
------------------- , ----~------------------------------------
14 1.4.2
Radiación Neta (RN).
Todo el balance de radiación incluídos los intercambios de radiación
de onda corta y larga, puede ser medido o calculado en conjunto. des­
preciando también los pequeños términos como fRG y Q.
El resultado
es una simplificación de la Ecuación 1 del balance de energía, que
se transforma en ló siguiente expt'esión:
( 1 - a ) RG
Denomino
RN
RB = ET + K
= ET
(2)
+ K~
,
Vemos, pues, que el valor de RN, llamado Radiación Neta, es más o
menos igual a la sUlna del calor latente de evapotranspiracíón y del
término que expresa la convección turbulenta o calor sensible.
A modo de ejemplo, Satterlund, 1972, citado por Lima (1986), pre senta
un
balance de energía para una superficie revestida con pasto, en un
día de verano, en zona templada:
Fuente
Ly/día
Radiación solar incidente
650
Emisión por la atmósfera
630
Radiación incidente total
1.280
Albedo (de la radiaci ón de onda corta (20%) )
130
Al bedo (de la radiación de onda larga (5%) )
32
Emisión por la superficie
792
Pérdida total de 1a radiación incidente
954
Radiación Neta (RN)
326
1.4.3 Conducción (Q).
Esta componente del balance de energía representa un elemento de al­
macenamiento, que actúa como absorbedor de calor durante períodos
del
alta radiación (período diurno, o de verano), y como abastecedor de )
calor durante períodos sin radiación (período nocturno).
\ La radiación neta disponible en la superficie del suelo ocasiona un
) flujo energético de la superficie hacia el interior del suelo.
Este
flujo resulta de un transporte molecular de calor, estableciendo un
)
gradiente térmico en el suelo.
La tasa media de almacenamiento de calor de un cuerpo dado, es función
de su densidad, de su calor específico, de su espesor y de su tempera­
tura (Lima, 1986; Ometto, 1981).
La expresión de la tasa de almacenamiento de calor por unidad de tiem­
po de un cuerpo de vol umen "v", que ocupa un área "A" está dada por:
Q=
) cp
t
x
V
A
x 6. T
( 3)
16 Donde:
Q:
tasa de almacenamiento de calor J>:
densidad t:
ti empo cp:
calor específico ~c:
capacidad calorífica de un cuerpo Z:
'i : espesor
A
LH:
variación de la temperaturtl media del cuerpo
En la Tabla 2, Lee (1980), presenta las propiedades térmicas de algu­
--
nos sustratos, pudiéndose observar que la capacidad calórica del,
y del material org5nico
--
aume~ta
con el contenido de humedad .
autor anota que la capacidad calorífica
de la parte aérea de
sue ~
El mismo
un b-G~-
que es relativamente pequeño, del orden de 2.5 Ly/ OC, por ejemplo,
para un bosque con 20 m de altura, o el equivalente a la capacidad
calorífica de una capa de 5 cm de suelo.
De ahí, que el principal
compartimiento almacenador de calor de un bosque sea el suelo.
1.4.4 Calor Latente de evaporación (ET) .
Este término representa la parte de energía incidente que se transfor­
ma en calor latente de vaporización con objeto de suministrar energTa
para la evaporación del agua de las superfic i es liquidas libres o del
suelo y para la transpiración de la vegetación.
17
TABLA 2. Propiedades
1980).
t~rmicas
Densidad
Materi a 1
1
(J' )
de algunos sustratos (Adaptada de Lee,
Calor especí­
fico (Cp)
Capacidad
térmica
(-FCp
Cal/cm /oC
1
Conductividad
t~rmi ca (Ko )
Cal/cm 3/min¡OC
g/cm 3
Cal/g/oC
Roca
2.7
0.18
0.49
0.25
Suelo arenoso
(20% humedad)
1.8
0.30
0.54
0.28
Sueloa rc i 11 oso
(20% humedad)
1.8
0.28
0.50
0.16
Turba (10% de
humedad)
0.4
0.55
0.22
0.015
Turba (40% de
humedad)
0.7
0.74
0.52
0.041
Turba (70% de
humedad)
1.0
0.82
0.82
0. 062
Madera
0.6
0.64
0.38
0.04
Agua
1.0
1.00
1.00
0.08
Hielo
0.9
0.50
0.45
0.32
Nieve
0.8
0.50
0.40
0.24
Aire
0.0012
0.24
0. 0003
0. 0036
V:I~~
La proporción de radiación solar transformada en calor latente de eva­
poración corresponde a 59 calorías por un mm de agua evapoY'(lda.
18 El calor latente de evaporación está dado por la expresión:
ET
=
Eo - 0,65 T Cal/g
Eo
597 Cal/g
T
Temperatura oC
=
Calor específico de evaporación.
~I ,~
/
1.4.5 Calor Sensible ( K ).
Este término representa la parte de energía solar recibida en la su­
perficie del suelo e intercambiada con la atmósfera por difusión tur­
bulenta.
La radiación neta disponible en la superficie del suelo, oca­
siona en el aire atmosférico, inmediatamente al contacto con él, una
transferencia molecular de energía.
En el caso del aire atmosférico,
ese transporte ocurre en una capa de espesor muy reducida y cercana a
la superficie del suelo.
Encima de esta capa laminar las moléculas
de aire atmosférico más energéticas tienden a moverse en sentido vertical en movimientos de baja amplitud, provocando lo que se llama pseu­
doconducción o difusión turbulenta.
Esta difusión turbulenta es en
realidad, movimiento convectivo, en pequeña escala, asociado a gradien­
tes de densidad entre los límites de la capa considerada.
1.5 BALANCE DE ENERGlA EN LA SUPERFICIE DEL SUELO DURANTE EL OlA Y
DURANTE LA NOCHE.
En el esquema siguiente aparece el balance de energía en la superfi­
cie del suelo durante el día y durante la noche.
I
19
RG
RA
Ec
,SUPERFIciE'
DEL SJELO
19 ' .
-...
OlA
NOCHE
ESQUEMA A
ESQUEMA B
De acuerdo con el esquema A, durante el día la superficie del suelo
recibe radiación solar (RG).
Parte de esta radiación es devuelta al
espacio debido al albedo (a).
El s uel o emite radi aci ón al espocio
en longitud de onda larga (RB) .
Parte de esa radiación será absor­
bida por 1a atmósfera, la cual a su vez la remitirá en todas las di­
recciones volviendo parte a 1a superficie del suelo en forma de ra­
diación atmosférica (Ra) ..
La superficie del suelo transfiere ener­
gía para la evaporación del agua en él contenida, dejando esa energía
en forma de calor latente de evaporación (El).
El suelo transfiere
energía desde la superficie hacia las capas más profundas por conduc­
ción (Q) y de la superficie hacia las capas de aire adyacente a él,
en la dirección de la atmósfera (K), siendo esa energía transferida
por difusión turbulenta.
20 Entonces,el balance de energía sera posítivo y estará dado por la
expresión:
(Ra + RG)
= (
De acuerdo con el
a
~
RB + K + ET + Q
esqu~na
(4 )
B, durante la noche la superficie del suelo
no recibe radiación solar y continOa perd i endo
rápid ~ mente
l a energía
que gana durante el d1a, pasando la temperatura de la superficie a
ser menor que la temperatura del aíre adyacente y que las capas más
profundas del suelo.
pasa a ser:
A partir de allí el balance de energía nocturno
emisión de radiaci6n de onda larga (RB) por la superficie
del suelo, en dirección de la atm6sfera.
En dirección a la superficie
del suelo, la atmósfera emite radiación en forma de onda larga (Ra)/
La superfic i e del suelo , con temperatura baja, propicia condiciones
para condensar el vaYor de agua atmosférico eri contacto con ella, re­
cibiendo así el calor latente de condensación (Ec).
La superficie
con temperatura baja, hace que la conducción de calor a las capas más
profundas del suelo (Q) sea con dirección hacia ella y finalmente el
aire que está inmediatamente encima de la superficie del suelo (K)
irá a transferir energía por medio de conducción para la superficie
del suelo.
Entonces, puesto que RB es numéricamente mayor, el balance de energia
se)"á nega ti va:
RB
= Ra
+ Ec + K + Q
(5 )
1.6
ESTIMACION DE LA RAOIACION SOLAR GLOBAL (RG).
En vista de la dificultad de obtener datos de radiación medida con
seguridad muchos autores ha n tratado de correlacionar la Radiación
Global (RG) recibida en un lugar determinado con la duración de la
insolación (nGmero de horas con so l) o con el grado de nubosidad del
cielo .
Para estimar la RG a partir de la insolación se ha recurrido a la
ecuación
de una linea recta, utilizando el análisis estadistico,
que permite medir el grado de asociación que ex i ste entre radiación
global e insolación.
La ecuación de una recta es de la forma:
y
=a
+ b X
En este caso "Y" se toma como la relación entre la energía solar que
llega
a la superficie de la tierra (RG) y la energia solar teórica
que existiria en ausencia de atmósfera (RA):
Y
,-
RG
RA
El valor de "X" es tomado como la relación existente entre 21 valo)'
del nGmero de horas de brillo solar que realmente hubo en un dfa (n)
con el nGmero máximo teórico de horas de brillo solar que habria en
ausencia de atr.lÓsfera {N) o sea:
Insolación relativa.
X= n
N
22 El término "b significa el ángulo de inclinación de la recta de
ll
regresión en relación con el eje de la abcisa.
El parámetro lIa
11
es el despl azami ento del punto de origen de 1a recta
en relación con el punto de orígen de un sistema de coordenadas orto­
gana 1es.
La ecuación para estimar la RG queda así:
RG/RA
= a
+ b (n/N) ó
RG
= RA ( a
+ b (n/N) ( 6)
Los valores de la energía solar teórica que llega al tope de la atmós­
fera (RA) se calculan en función de otras variables como, latitud del
lugar, declinación solar, ángulo horario.
RA se encuentran en el Apéndice A, según la latitud del lugar
entre 50 oS y 50 °N.
N
;Tabla 11.
Se encuentra en la Tabla l.
Apéndice A.
Esta ecuación (6)ha venido siendo ampliamente utilizada, aunque impli­
ca la definición de los parámetros lIa" y "b o a + b.
ll