1 UNIDAD III: GRAFOS Definición: Llamaremos grafo a una terna G

MATERIAL TEÓRICO
2º Cuatrimestre Año 2013
Prof. María Elena Ruiz
Prof. Carlos Roberto Pérez Medina
UNIDAD III: GRAFOS1
Definición: Llamaremos grafo a una terna G= (V, A, ϕ), donde V y A son conjuntos
finitos, no vacíos y ϕ una aplicación que hace corresponder a cada elemento de A un
par de elementos de V.
Los elementos de V son los vértices (o nodos) de G y los elementos de A son las aristas
(o arcos) de G.
La representación gráfica de un grafo se efectúa asociando a cada vértice un punto del
plano del dibujo y a cada arista una línea que une los puntos asociados con los vértices.
Observación
El trazado de un grafo no es un problema de geometría métrica, debido a esto
no interesa la forma de las líneas que unen a los vértices, solamente nos
interesa visualizar las relaciones, las conexiones o vínculos existentes.
Tipos de grafos
Existen diferentes tipos de grafos, según las relaciones que puedan establecer entre
vértices y aristas:
-
Grafo sencillo (o grafo propiamente dicho): cuando dos vértices se conectan
por una sola arista (o arco).
Multigrafo: cuando dos vértices están conectados por más de una arista.
Pseudografo: cuando un vértice puede unirse con él mismo (lazo o bucle).
Ejemplos:
1
Este apunte teórico se efectuó sobre la base del material teórico realizado para la misma asignatura en el
cursado 2011 por la profesora Virginia Navarro.
1
Definiciones:
- G es de orden n si tiene n vértices.
- El grado de un vértice es el número de aristas que inciden en él.
- Un vértice se dice aislado si su grado es nulo y pendiente si su grado es 1.
- Un lazo es una arista cuyos dos extremos coinciden en el vértice.
- Dos aristas se dicen adyacentes cuando tienen un vértice en común.
- Si (a, b)) es una arista de G, los vértices a y b son adyacentes.
- Un vértice de G se llama vértice par o vértice impar de acuerdo a que el grado del
mismo sea par o impar.
- Dos o más aristas se llaman múltiples o paralelas si tienen por extremos los
mismos vértices.
- A todo grafo G=(V, A)) se le asocia el par ordenado de números naturales G=(m, n)
siendo m el número de vértices y n el número de aristas.
- Se llama grafo etiquetado a aquel en el que cada vértice está asociado a una letra o
número.
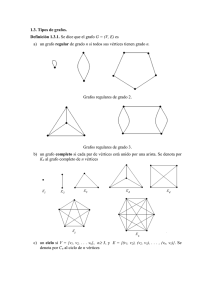
- Un grafo se llama k-regular
regular, cuando todos los vértices de G tienen igual grado k.
- Todo grafo sencillo (es decir que no tiene aristas múltiples ni lazos o bucles) de n
vértices en el que todo par de vértices determina una arista (o arco), se denomina
grafo completo de n vértices. En todo grafo completo
to de n vértices, todos los
vértices tienen n-11 grado y el número de aristas es
.
Ejemplos de grafos completos
Grafo bipartito
Un grafo G=(V, A) es bipartito si el conjunto V puede ser particionado en dos
subconjuntos, V1 y V2, tal que cada arista de G tiene un extremo en el conjunto V1 y otro
extremo en el conjunto V2.
En particular, si G es un grafo tal que cada vértice del conjunto V1 es adyacente a cada
vértice del conjunto V2, entonces el grafo G es bipartito completo.
Un ejemplo aplicativo sería el siguiente:
2
En una empresa deben ser realizadas 7 tareas
( t1 , t2 , t3 , t4 , t5 , t6 , t7 ) y se dispone de 5
operarios ( o1 , o2 , o3 , o4 , o5 ) . Si el operario o1 es
capaz de realizar las tareas t1 y t3 , el operario
o2 es capaz de realizar las tareas t4 y t6 , o3 la
tarea t 2 , o4 las tareas t5 y t6 y finalmente el
operador o5 es capaz de realizar las tareas
t4 y t7 . Esta situación puede ser representada
mediante el siguiente grafo bipartito:
Grafos no dirigidos
El grafo G=(V, A) se dice no dirigido si cada arista de A se asocia con un par no
ordenado de vértices de V.
Grafos dirigidos o digrafo
El grafo G=(V, A) se dice dirigido (digrafo) si cada arista de A se asocia con un par
ordenado de vértices de V, los cuales no necesariamente tienen que ser distintos.
Ejemplo:
Definiciones de conceptos orientados:
-
Sea (a, b) una arista o arco de G, entonces a es el extremo inicial y b el extremo
final. Si el arco tiene igual extremo inicial que final, se trata de un lazo o bucle.
Se dice que dos arcos son paralelos si tienen el mismo extremo inicial y el mismo
extremo final.
Cuando dos arcos tienen un extremo en común y son distintos se llaman arcos
adyacentes.
Se dice que dos arcos son opuestos si el extremo inicial y final de uno coinciden
con los extremos final e inicial de otro respectivamente.
Subgrafo
Un grafo S es un subgrafo de un grafo G si los vértices y las aristas de S están incluidos
en los vértices y aristas de G.
3
Los subgrafos pueden tomarse respecto de un vértice (se anula el vértice y todas las
aristas que en él inciden) o bien respecto de una arista (se anula la arista).
Ejemplo:
Grafo G
Subgrafo respecto del
vértice c
Subgrafo respecto de la arista
(c, d)
DEFINICIONES:
-
-
Un camino (o paso) es una sucesión de arcos adyacentes tales que el extremo final
de uno coincide con el extremo inicial del siguiente.
Un camino es simple si no se repiten arcos.
Un camino es elemental si no se repiten vértices, excepto el vértice inicial y final.
Todo camino nulo es elemental y simple, ya que en él no se repiten arcos ni
tampoco vértices.
Un circuito es un camino finito en el cual el vértice inicial coincide con el final, en
este caso se habla de camino cerrado. En caso contrario se dice que el camino es
abierto.
La longitud de un camino es el número de arcos de la sucesión.
Un bucle es un circuito de longitud 1.
Ejemplo:
G = (V , A )
V = {u , v, w, y , x}
A = {a, b, c, d , e, f , g , h} =
= {( u , u ) , ( u , v ) , ( v, w ) , ( y , v ) , ( w, y ) , ( w, x ) , ( x, w ) , ( x, y )}
Ejemplos de arcos adyacentes del digrafo G :
( u, v ) y ( v, w ) ; ( w, x ) y ( x, w ) ; ( w, x ) y ( x, y ) , es decir,
b y c ; f yg ; f y h
Ejemplos de caminos del digrafo G :
4
a ) C1 : u , b, v, c, w, f , x
b) C2 : v, c, w, e, y
c) C3 : w, f , x, h, y, d , v, c, w
El camino C1 es: de longitud 3, abierto (el vértice inicial no coincide con el vértice
final), simple (no se repiten arcos) y elemental (no se repiten vértices)
El camino C2 es: de longitud 2, abierto (el vértice inicial no coincide con el vértice
final), simple (no se repiten arcos) y elemental (no se repiten vértices)
El camino C3 es: de longitud 4, cerrado (el vértice inicial coincide con el vértice
final), por lo tanto es un circuito, simple (no se repiten arcos) y elemental (no se
repiten vértices)
En el digrafo G , el bucle u , a , u es un circuito de longitud 1.
Un subgrafo dirigido del digrafo G es el siguiente
grafo S pues los vértices y las aristas de S están
incluidos en los vértices y aristas de G
Definiciones
-
Un dígrafo se dice fuertemente conexo si entre dos vértices cualesquiera de este
existe un camino de cualquier longitud que va de uno a otro.
Todo subgrafo fuertemente conexo de un grafo se denomina componente
fuertemente conexa.
Ejemplos:
El digrafo de de la Figura 1 es fuertemente conexo, en cambio el de la Figura 2 no es
fuertemente conexo porque no existe un camino de u a y ; ni de w a y ; ni de x a y .
5
El subgrafo dirigido de la Figura 3 es una componente
fuertemente conexa del digrafo de la Figura 2.
En el caso de un grafo no dirigido se tienen conceptos equivalentes a los de un digrafo.
Conceptos de Grafos no dirigidos
- Una cadena es una sucesión de aristas adyacentes.
En el grafo de la Figura 4, algunas cadenas que podemos encontrar son:
a ) C1 : u , a, v, b, w
b) C2 : u , c, w, d , x
c) C3 : x, e, y, f , u , c, w, b, v
-
Un ciclo es una cadena finita en la cual el
vértice inicial coincide con el vértice final.
En el grafo de la Figura 4 son ciclos:
a) C1 : u, a, v, b, w, c, u
b) C2 : w, d , x, e, y, f , u, c, w
- La longitud de una cadena es el número de aristas de la sucesión.
Siguiendo con el ejemplo anterior, tenemos que la longitud de C1 es: 3, y la de C2 es: 4
-
Un grafo es conexo si entre dos vértices cualesquiera y distintos existe una cadena
de cualquier longitud.
El grafo de la Figura 4 es conexo, pero el grafo de la Figura 5 no es conexo, pues no
existe una cadena de u a x , por ejemplo.
6
-
Un subgrafo de un grafo dado que sea conexo se llama componente conexa.
El grafo de la figura 6 es una componente conexa del grafo
de la Figura 5
PROBLEMA DE LOS PUENTES DE KÖNIGSBERG
Este fue el primer problema, en orden cronológico, de los resueltos con métodos
incluidos en el estudio de grafos. A quien se le atribuye la solución es al famoso
matemático suizo Leonahard Euler (1707-1783).
La cuidad de Königsberg (hoy Kaliningrado), en Prusia Oriental, está situada en las
márgenes del Río Pregel y sobre dos de sus islas, las distintas partes de la cuidad están
conectadas entre ellas por siete puentes, según el siguiente esquema:
Los domingos la gente que vivía en la cuidad salía de paseo, como es costumbre en las
ciudades alemanas y entonces surgió la pregunta:
¿Es posible efectuar un paseo a pie, tal que utilizando exactamente una vez cada uno
de los puentes, se vuelva al punto inicial?
El matemático L. Euler, a partir de considerar
un caso general, logró dar las condiciones
necesarias para que tal recorrido realmente
fuera posible. La idea genial de Euler fue
representar la ciudad de Königsberg como un
grafo en el que las cuatro partes de la misma
eran los vértices y los siete puentes eran las
aristas:
7
Efectuar el paseo antes mencionado, es equivalente a dibujar el diagrama anterior de
un solo trazo, sin levantar el lápiz ni pasar dos veces por una misma arista y finalizar
en el vértice del cual se partió. En este caso en particular, no puede ser realizado dicho
paseo, aún cuando no se hubiese pedido regresar al punto de partida.
En terminología de grafos, el problema hubiera tenido solución si el grafo contuviera
una cadena simple (no repite arista) y cerrada (el vértice inicial coincide con el vértice
final) que recorriera todas las aristas exactamente una vez, a dicha cadena se la
denomina recorrido euleriano cerrado o directamente recorrido euleriano.
Si la cadena es simple tal que recorriera todas las aristas exactamente una vez pero el
vértice inicial no coincide con el final, se la denomina recorrido euleriano abierto.
A los grafos que contienen al menos un recorrido con estas particularidades se los
denominan grafos eulerianos.
TEOREMAS:
1. Un grafo G posee un recorrido de Euler si y sólo si G es conexo y todo vértice
tiene grado par.
2. En un grafo conexo G existe un recorrido de Euler si y sólo si existen dos vértices
impares o ninguno impar.
Ejemplos:
En el grafo de la figura 1, los únicos vértices de grado impar son los vértices c y f ,
podemos asegurar por el Teorema 2 que existe un recorrido euleriano en dicho grafo.
Por ejemplo, f , 6, c , 5, d , 3, t ,1, a , 2, e, 4, c es un recorrido euleriano abierto.
El grafo G de la Figura 2 se obtiene a partir del grafo de la figura 1 agregando una arista
que une a los vértices c y f , este nuevo grafo tiene todos los vértices de grado par. El
teorema 1 nos asegura que posee un recorrido euleriano. Por ejemplo:
e, 4, c , 7, f , 6, c , 5, d , 3, b ,1, a , 2, e , dicho recorrido es un recorrido euleriano cerrado.
COLOREO DE GRAFOS
El problema de coloración de mapas surgió a mediados del siglo XIX. En ese entonces
se pensaba que bastaban cuatro colores para colorear cualquier mapa dibujado en un
plano, de tal modo que no existan dos regiones distintas que compartan una frontera
común con el mismo color.
8
En 1976 se demostró que esta conjetura era cierta, con la ayuda de cálculos realizados
gracias al potencial de las computadoras modernas.
Para modelar este problema a través de un grafo se procede del siguiente modo.
Supongamos por ejemplo que deseamos colorear el mapa M que se muestra en la
siguiente Figura
Si identificamos cada región con un vértice y dibujamos una arista entre aquellos
vértices que compartan una frontera en común, obtendremos el grafo asociado al mapa
M. En este caso obtenemos el siguiente grafo asociado G:
Definiciones:
1. El coloreo de un grafo consiste en darle colores a los vértices de manera tal que a
vértices adyacentes correspondan colores diferentes.
2. La cantidad mínima de colores necesarios para colorear los vértices de un grafo G es
llamada número cromático de G y se la nota como χ ( G ) .
9