FLEXIÓ COMPUESTA Y COLUM AS ESBELTAS Dr. Alfonso Huber

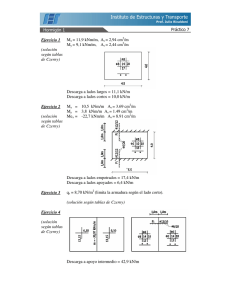
FLEXIÓ COMPUESTA Y COLUMAS ESBELTAS
Dr. Alfonso Huber
Se propone un método para dimensionar o comprobar la capacidad portante de columnas esbeltas de
hormigón armado basado en el cálculo de deformaciones de segundo orden para la sección crítica. Para
esta sección se obtienen las curvas de interacción entre la fuerza normal y el momento mediante las
ecuaciones de equilibrio y limites de deformaciones específicas en acuerdo con la versión 2002 del
reglamento CIRSOC 201. Estas ecuaciones permiten también determinar la resistencia nominal en flexión
compuesta de secciones rectangulares de hormigón armado en forma sencilla sin necesidad de tablas.
Flexión Compuesta
En Fig.1a se muestra una sección solicitada por una fuerza normal y un momento y ciertos limites
(ver Tabla 1) de las deformaciones específicas y la hipótesis simplificada para la distribución de las
tensiones. Es conveniente usar valores adimensionales Fig. 1b). Tracción es positiva y compresión es
negativa. A continuación están indicadas las fórmulas adimensionales de equilibrio, que son elementales.
nn = Nn /(bdf'c )
mn = Mn /(bd2 f'c )
w = As fy /(bdf'c )
nn = w - w' - 0,85 a/d mns = mn - nn ds /d = 0,85a/d(1 - 0,5a/d) + w'.ds /d
Un caso especial es la armadura simétrica que se usa normalmente en columnas que es
convenientemente presentado por un diagrama de interacción entre N -M con los siguientes tres tramos:
w = w': nn = - 0,85a/d
flexo-compresión de gran excentricidad:
mn = - nn/2(h/d + nn /0,85) + w'.ds /d
(nL < nn < 0)
flexo-compresión de pequeña excentricidad:
mn = c(- nL /2(h/d + nL /0,85) + w'.ds /d )
c = (h/d + 2w +nn )/(h/d + 2w +nL )
(nn <= nL )
(nn <= nL )
flexo-tracción: mn = (w - nn/2)ds/d
(nn > 0)
La resistencia de diseño es obtenido por medio del factor de reducciónf.
f = 1.317 - 1.111c/d
para w = w': f = 1,317 + 1,309nn /b1 (n1 > nn > n2 )
La Fig.2a representa un diagrama de interacción para w = w' = 0,15 que es ligeramente conservador
respecto a los conocidas soluciones "exactas". Se compone de tres tramos: flexo-tracción, gran y pequeña
excentricidad en flexo-compresión basado en las ecuaciones de equilibrio. El valor de la reducción de
resistencia f (Fig.2b) puede expresarse entre los límites de c/d 0,375 y 0,6 por n1 y n2 .
Tabla 1 Limites de a/d y de n
Hormigón (MPa)
<=30
35
40
b1
0,85
0,81
0,77
a/d=0,375b1
0,318
0,304
0,289
0,259
a/d=0,545b1
0,463
0,441
0,420
0,376
a/d=0,6b1
0,510
o,486
0,462
0,414
n1
- 0,271
- 0.258
- 0,245
- 0,220
nL
- 0.394
- 0,375
-,0357
- 0,320
n2
- 0,433
- 0.413
- 0.393
- 0.352
- nL /2(1,1 + nL/0,85)
0,125
0,124
0,121
0,115
45
0,69
Inestabilidad de Columnas
Las solicitaciones en una sección crítica dependen - a diferencia del análisis ordinario en flexocompresión - también de la deformación de la columna.El cálculo de las deformaciones de la columna
esbelta se realiza con el conocido método del análisis estructural para calcular deformaciones que permite
obtener los momentos de segundo orden. Con el momento total se dimensiona la armadura para la sección
mas solicitada o se puede determinar la capacidad de carga de una columna. El problema de la
inestabilidad de las columnas es reducido a uno de resistencia. Para la zona de grandes excentricidades
(nn > nL ) se obtiene resultados conservadores, porque la carga que produce inestabilidad pude ser mayor
(ver la curva en Fig. 2a). Se parte de una forma parabólica de la curvatura de segundo orden a la cual se
suma la de los momentos de primer orden.
f/d = (1/d2) ò k.M' dl
donde k es la curvatura adimensional k = d/r = c.ku , con ku = 2fy.d/Es .ds . El coeficiente c es <= 1
(Fig.2b) y ku es limitado al comienzo de la tensión de fluencia en las armaduras. La Fig.3 muestra una
columna ménsula con diferentes cargas y los correspondientes gráficos de curvaturas. La flecha puede
expresarse, tomando
ko = c ku - k1 - k2 - k3 , por: f/d = (5c + k1 /ku - k2 /ku - 2k3 /ku )(ku /48)(l/d)2 . Para
la relación de las diferentes curvaturas con la máxima curvatura se usa la hipótesis ki /ku = c.min /mn.
Inicialmente debe estimarse estas relaciones y luego corregirlos en base a los datos obtenidos.
Generalmente son suficientes dos iteraciones. El momento nominal reducido se obtiene finalmente
sumando los momentos de primer y segundo orden. La resistencia de diseño es obtenido mediante el
coeficiente f. . En el diseño se parte con la resistencia de diseño que se convierte a la resistencia
nominal substituyendo nu /f por nn, lo que lleva a resolver una ecuación de 2o grado para obtener f si n1
> nn > n2 .
En el Apéndice se muestran algunas aplicaciones prácticas.
Apéndice
Datos: H 20 f'c = 20 MPa acero fy =420 MPa sección de hormigón cuadrada 0,4x0,4 m (Fig. 4a) b1 =
0,85 d = 0,36 m ds = 0,32 m bdf'c = 2880 kN
bd2f'c .= 1037 kNm (los datos son válidos para todos
los ejemplos)
Ejemplo 1: flexión simple, determinar la resistencia de diseño para As =8,04 cm2 (4 f 16 mm) A's = 0
w = 8,04. 42/2880 = 0,117 a/d = w/0,85 = 0,138 mn = 0,117(1 - 0,138/2) = 0,109 Mn = 0,109.1037 =
113,0 kNm f = 0,9 resistencia de diseño = 0,9.113 = 102 kNm
Ejemplo 2: determinar elmáximo momento nominal que la sección puede resistir sin armadura de
compresión (f es todavía 0,9)
max. a/d = 0,318 w = 0,85a/d = 0,270
mn = 0,270(1 - 0,318/2) = 0,227
Mn = 0,227.1037 = 235
kNm
Ejemplo 3: determinar el máximo momento nominal de la sección para As = A's = 8,04 cm2 a/d = 0
(esto resulta del planteo formal; en realidad, el esfuerzo de compresión será compartido por el hormigón y
la armadura de compresión)
mn = 0,117.0,32/0,36 =0,104 Mn = 0,104.1037 = 108,0 kNm
Ejemplo 4: ídem ejemplo 3, pero con As = 8,04 cm2 y A's = 4,02 cm2
0,85a/d = w - w' = 0,059 a/d = 0,069 mn = 0,059(1,111/2 - 0,069/2) + (0,117 + 0,059),0,32/2.0,36 =
0,109
Mn = 112,7 kNm
Nota: la armadura de compresión no es efectivo ni necesaria para c/d < 0.375 y para c/d > 0,375 el
coeficiente f castiga en mayor grado la resistencia de diseño
Ejemplo 5: determinar la armadura simétrica en flexo-compresión
Nn = - 1000 kN Mn = 265 kNm nn = - 0,347 > nL = - 0,394 mn =0,256
0,256 = 0,347/2(0,4/0,36 - 0,347/0,85) + w.0,889 resolviendo resulta w =0,151 y As = A's = 10,4 cm2
Ejemplo 6: determinar el momento total para la sección media de una columna biarticulada con carga
excéntrica (Fig. 4b) Nn = - 1000 kN nn = - 0,347 > nL < nL c =1 pero f < 0,9 l = 12 m e = 0,06 m
M1n = 60 kNm
m1n = 0,0579
ku = 4,725.10-3 l/d = 33,3
ku /48.(l/d)2 = 0,109 f/d = (5 + k1
/ku )0,109
con k1 /ku = 0,2 (estimado) f/d = 0,567
mn = 0,0579 +0,347.0,567 = 0,255
nuevo valor k1 /ku = 0,0579/0,255 = 0,227 f/d = 0,570 mn = 0,256 k1 /ku = 0,226
Mn = 265 kNm; la armadura fue determinado en el Ejemplo 5 anterior . Fig. 2 muestra los diagramas de
interacción de mn, nn, F y k.
Ejemplo 7: columna como Ejemplo 6 Nn = - 2000 kN nn = - 0,694 < n2 y f
0,65 M1n = 120 kNm m1n = 0,116 f/d = (5c + k1 /ku ).0,109
es entonces
f=
con k1 /ku = 0,3 y c = 0,8 (estimados) f/d = 0,469 mn = 0,116 + 0,694.0,469 = 0,441 = 0,8(0,394/2(1,111
- 0,394/0,85) + w.0,889) w =0,476 nuevos valores:
c = (1,111 + 2.0,476 - 0,694)/(1,111 + 2.0,476 - 0,394) = 0,820
k1 /ku = 0,82.0,116/0,441 = 0,216 f/d = 0,470 mn = 0,442 w = 0,462
c =0,818 (satisfactorio) As = A's = 31,8 cm2 (7f25 mm = 34,4 cm2 ; número máximo por capa para el
ancho 0,4 m de la columna). La carga resistente de diseño es Nu = 0,65.2000 = 1300 kN
Ejemplo 8: determinar para una columna ménsula con cargas verticales y horizontales la armadura (Fig.
4c); altura 6,0 m e = 0,06 m carga horizontal distribuida sobre la altura wn = 4 kN/m Nn = - 1000 kN
M1n = 60 M3n = 72 kNm para la sección crítica en el pie de la columna nn = - 0,347 m1n = 0,058 m3n =
0,069 su suma 0,127 f/d = (5 + k1 /ku - 2k3 /ku ) 0,109 con k1 /ku = 0,2 y k3 /ku = 0,2 (estimados) f/d =
0,523 mn = 0,127 + 0,347.9,523 = 0,308 nuevos valores: k1 /ku = 0,188 k3 /ku = 0,224 f/d = 0,517 mn
= 0,306 una segunda iteración da k1 /ku =0,190 y k3 /ku = 0,225 que es satisfactorio
0,306 = 0,122 + w'0,889 w' = 0,207 y As = A's = 14,2 cm2
Ejemplo 9: determinar la capacidad portante de la columna del Ejemplo 6 para As = A's = 8,04 cm2 w =
0,117
k1 /ku =0,2 y c = 1 (estimados) e/d = 0,167 f/d = 5,2.0,109 = 0,567 m1n = 0,167.nn
mn = - nn (0,167 + 0,567) = - 0,734 nn = - nn /2(1,111 + nn /0,85) + w'.0,889 la solución de la ecuación
cuadrática da nn = - 0,295 m1n = 0,049 mn = 0,217 k1 /ku = 0,228 nuevos valores: f/d = 0,570 nn
= - 0,294 > nL < n1 confirma c = 1
mn = 0,217 k1 /ku = 0,226 capacidad portante
Nn = - 0,294.2880 = - 847 kN
f = 1,317 - 1.540.0,294 = 0,87 y Nu = 0,87.847 = 737 kN
Bibliografía
•
•
•
CIRSOC “Proyecto de Reglamento Argentino de Estructuras de Hormigón” 2002
Huber A. “Dimensionamiento y análisis directo de columnas de hormigón armado” XI Jornadas
de Ingeniería Estructural, AIE, 1983.
CEB/FIP “Manual of buckling and instability” CEB Bulletin o.123, Dic. 1977