Formulaire de trigonométrie

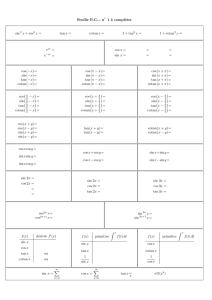
Université Paul Cézanne
Faculté des Sciences et Techniques
Lycée Blaise Pascal
TSI 1 année
Fiche : Formules
de trigonométrie
Formulaire
de trigonométrie
cotan x
cos2 x + sin2 x = 1
x
1 + tan2 x =
1 + cotan2 x =
tan x
sin x
1
cos2 x
1
sin2 x
cos x
1
Valeurs remarquables
π
3
√
3
2
√
2
2
π
4
π
6
1
2
√
1
2
2
√
3
2
0
sin x
0
cos x
1
π
4
√
2
2
√
2
2
1
2
√
3
2
tan x
0
cotan x
indéfini
1
√
3
√
3
π
3
√
3
2
π
2
1
1
2
0
1
√
indéfini
1
1
√
3
3
0
π
−x
2
π−x
x
cos (−x) = cos x
cos (π + x) = − cos x
cos (π − x) = − cos x
sin (−x) = − sin x
sin (π + x) = − sin x
sin (π − x) = sin x
tan (−x) = − tan x
tan (π + x) = tan x
tan (π − x) = − tan x
−x
π+x
+ x = − sin x
2
π
sin
+ x = cos x
2
π
tan
+ x = − cotan x
2
cos
π
− x = sin x
2
π
sin
− x = cos x
2
π
tan
− x = cotan x
2
cos
π
Addition des arcs
cos(a + b) = cos a cos b − sin a sin b
sin(a + b) = sin a cos b + cos a sin b
cos(a − b) = cos a cos b + sin a sin b
sin(a − b) = sin a cos b − cos a sin b
cos(2x) = cos2 x − sin2 x
1 + cos(2x)
2
1 − cos(2x)
sin2 x =
2
= 1 − 2 sin2 x
sin(2x) = 2 cos x sin x
p+q
p−q
cos
2
2
p+q
p−q
cos p − cos q = −2 sin
sin
2
2
p+q
p−q
cos
2
2
p+q
p−q
sin p − sin q = 2 cos
sin
2
2
cos p + cos q = 2 cos
cos a cos b =
tan a + tan b
1 − tan a tan b
tan a − tan b
tan(a − b) =
1 + tan a tan b
tan(a + b) =
cos2 x =
= 2 cos2 x − 1
4
π
6
Symétries
π
+x
2
3
√
2
2
x
sin(p + q)
cos p cos q
sin(p − q)
tan p − tan q =
cos p cos q
sin p + sin q = 2 sin
1
(cos (a + b) + cos (a − b))
2
sin a sin b =
1
(cos (a − b) − cos (a + b))
2
tan p + tan q =
cos a sin b =
1
(sin (a + b) − sin (a − b))
2
Tangente du demi-angle
x
En notant t = tan , on a :
2
cos x =
Module MA102 - Géométrie et polynômes
1 − t2
1 + t2
sin x =
1
2t
1 + t2
tan x =
2t
1 − t2
Année 2010/2011