Matemáticas Básica Probabilidad

EJE: MANEJO DE LA INFORMACIÓN
La Probabilidad
Muchos de los eventos que ocurren en la vida diaria no pueden ser
predichos con exactitud desde antes por diversas razones, pues la
mayoría de los hechos están influidos por factores externos.
Además, existen aquellos sucesos que están directamente
influidos por el azar, es decir, por procesos que no se está
seguro de lo que va a ocurrir. Sin embargo, la probabilidad nos
permite acercarnos a esos sucesos y estudiarlos, ponderando las
posibilidades de su ocurrencia y proporcionando métodos para tales
ponderaciones.
Precisamente, algunos de esos métodos proporcionados por la probabilidad nos llevan a
descubrir que algunos sucesos tienen una mayor o menor probabilidad de ocurrir que la
ponderación asignada a través del sentido común. Nuestros sentidos, la información
previa que poseemos, nuestras creencias o posturas, nuestras inclinaciones, son algunos
de los factores que intervienen para no permitirnos hacer ponderaciones reales y
sistemáticas. La probabilidad nos permitirá estudiar los eventos de una manera
sistemática y más cercana a la realidad, retribuyéndonos con información más precisa y
confiable y, por tanto, más útil para las disciplinas humanas.
A continuación te
presentamos algunas definiciones y actividades que te servirán de apoyo para reafirmar
tus conocimientos de los contenidos del programa de estudios en relación con el tema de
probabilidad.
1.1 Conteo y Diagramas de Arbol
Un recurso muy útil para conocer todos los posibles resultados de un experimento
aleatorio son los diagramas de árbol.
Ejemplo: Al lanzar dos dados, ¿cuántos resultados posibles hay en total?
¿Cuántos de los resultados posibles son favorables al evento: la suma de los números
que salen es un número impar?
Para encontrar la respuesta, en tu cuaderno elabora y completa un diagrama de árbol
como el siguiente:
Tomado de la Guía Interactiva para Secundaria 2008.
Una vez que los alumnos hayan calculado los resultados posibles de varios experimentos,
llámele “Espacio muestral” a cada uno de dichos conjuntos y pida a los alumnos que ellos
escriban su definición con sus propias palabras.
Si fuera necesario consolidar la noción de experimentos aleatorios y la descripción del
espacio muestral, se les puede pedir a los alumnos que ellos inventen experimentos
aleatorios y determinen el espacio muestral. Seguro que recordarán algunos de los que
manejaron en la escuela primaria. Pueden intercambiar experimentos para determinar los
espacios muestrales.
En el caso de que existan más de un suceso a observar, habría que contar el número de
veces que pueden ocurrir todos los sucesos que se desean observar, para ello se utiliza el
principio fundamental de conteo:
Si un suceso se puede presentar de n1 formas, y otro se puede presentar de n2 formas,
entonces el número de formas en que ambos sucesos pueden presentarse en ese orden
es de n1·n2.
Ejemplo: Al lanzar dos dados cada uno de estos puede caer de seis formas diferentes;
entonces el número de formas en que pueden caer al ser lanzados juntos es 6 x 6 = 36
En otras palabras, basta multiplicar el número de formas en que se pueden
presentar cada uno de los sucesos a observar.
1.2. Eventos
Cuando se realiza un experimento, que es cualquier proceso que produce
un resultado o una observación, se van a obtener un conjunto de valores. A
este conjunto de valores que puede tomar una variable se le denomina
espacio muestral.
Por ejemplo: Si se tiene un dado cualquiera, el espacio muestral
(EM) es
EM={1,2,3,4,5,6}.
Si existen más de una variable, el espacio muestral está formado por las combinaciones
de valores de cada una de las variables.
Si tomamos un subconjunto cualquiera del espacio muestral tenemos lo que se denomina
un evento, y si éste consta de un solo elemento entonces es un evento elemental.
Como se puede uno imaginar, existen eventos que siempre, no importa
el número de experimentos o su situación, ocurren, y en cambio existen
otros que nunca ocurren. Los que siempre ocurren son los eventos
seguros, y los que nunca son los eventos imposibles.
Ejemplo: “días de la semana en que sale el sol” es un evento seguro ya que todos los
días sale el sol (aunque esté nublado)
Al lanzar un dado “el numero que cae es mayor que 6”; es un evento imposible ya que el
dado solamente tiene seis caras enumeradas.
NOTA: Solicitar a los alumnos que nombren algunos eventos seguros y otros imposibles
Sin embargo, no todos los resultados son al azar, pues si un experimento es cualquier
proceso entonces los resultados pueden tomar cualquier tipo de valor. Por esta razón, se
define como experimento aleatorio al proceso en el que se pueden predecir con certeza
la ocurrencia de sus eventos, con excepción del seguro o del imposible. Hay que hacer la
observación que esta definición habla en términos generales y no específicamente sobre
algún experimento en particular.
A aquélla variable que está asociada a un experimento de este tipo se le denomina
variable aleatoria.
1.3 Probabilidad empírica y teórica de un evento.
Una urna contiene 3 canicas, una azul (a), una blanca (b) y otra café (c). Después
de revolver las canicas, se extrae una al azar, se anota su color y se regresa a la
urna. El experimento anterior se repitió 20 veces y se obtuvieron los siguientes
resultados:
a) ¿Cuál crees que será el color de la canica que se extraiga la próxima vez y
por qué?
Se repitió varias veces el experimento anterior y se obtuvieron las siguientes series de 20
extracciones:
Solicitar a los alumnos que realicen el mismo experimento
y anotar los resultados que
obtuvieron en la serie de 20 extracciones.
Guiar el análisis con las siguientes preguntas:
¿Obtuviste los mismos resultados que en las series anteriores?
¿Cuántas veces te salió una canica blanca?
¿Cuántas veces salió una canica azul?
¿Cuántas veces una café?
De acuerdo con el experimento, una vez que se extrae y anota el color de la canica se
regresa a la urna. Entonces, antes de realizar una nueva extracción ¿cuántas canicas y
de qué color hay en la urna?
Si un color aparece dos veces seguidas, ¿es más probable que la próxima canica sea o
no del mismo color? ¿por qué?
Si repites 10 veces el experimento podrías predecir cuántas veces extraerás una canica
café?, ¿y una blanca?
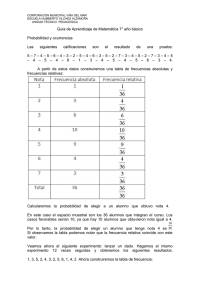
Realiza este experimento solamente 10 veces y completa la tabla siguiente:
Evento
No. De veces Frecuencia relativa
No. De veces que
que se extrae
se espera extraer
Una canica azul
__ /10
Una
__ /10
canica
blanca
Una canica café
Total
__ /10
1
El problema que se plantea en esta pregunta implica que los alumnos pongan en juego
sus intuiciones y conocimientos sobre cómo determinar los resultados posibles al realizar
un experimento aleatorio. Particularmente se averigua sobre las reflexiones y los
argumentos en los que los alumnos se basan para dar sus respuestas. En este caso, los
valores de las probabilidades frecuenciales de los eventos simples: extraer una canica de
color azul; extraer una canica de color blanco y extraer una canica de color café, no son
iguales a los valores de sus probabilidades clásicas (que son de 1/3). Esto sucede porque
20 extracciones podrían ser “pocas” para que el valor de la probabilidad frecuencial
(frecuencia relativa) se acerque o sea igual al de la clásica. Los alumnos deben saber que
la probabilidad frecuencial es una medida obtenida de la experiencia de algún fenómeno o
experimento aleatorio que permite estimar a futuro un comportamiento. Sin embargo, no
es definitiva por lo que es importante saber interpretar los resultados que se obtienen.
Algunos alumnos considerarán que los resultados obtenidos en las 20 extracciones son
“suficientes” y “representativos” para determinar que en la próxima extracción la canica
será de color blanco. En este caso, en la retroalimentación se busca que los alumnos
reflexionen si existen otras combinaciones en que se pudieran dar las 20 extracciones.
Los alumnos que seleccionan la opción b) sólo consideran la información proporcionada
por la última repetición del experimento aleatorio. Los alumnos que seleccionan la opción
c), observan la aparición de una racha a favor de un resultado, por ejemplo, el número de
veces que se ha extraído la canica blanca y creen que eso disminuye la probabilidad de
salga blanca.
Para cualquiera de esas situaciones, se le sugiere dar a los alumnos la oportunidad de
resolver problemas que requieran la recolección o simulación de sus propios datos para la
toma de decisiones. Lo cual significa, introducir la enseñanza de la probabilidad de modo
experimental y confrontar las creencias personales de sus alumnos, de carácter
determinista.
Finalmente, los alumnos deben saber que para obtener la probabilidad clásica de un
evento, no se requiere de la realización de experimentos como en la probabilidad
frecuencial, sino de conocer dos datos: el de todos los resultados posibles que se pueden
dar en el experimento, y el de los resultados favorables del evento que se observa. Por lo
que la probabilidad clásica que un evento es diferente de la probabilidad frecuencial.
Después de realizar muchos experimentos, la probabilidad frecuencial debe parecerse a
la clásica.
Ahora considera los 60 resultados que aparecen en las series 1, 2 y 3 al inicio del
problema y realizando el conteo completa la siguiente tabla:
Evento: extraer
No. De veces que se Frecuencia relativa
extrae
Una
canica
___ /60
blanca
Una canica azul
Una canica café
Totales
1
Calcula la probabilidad clásica de cada evento
Evento: extraer
No. de resultadosfavorablesal evento
No. totalde resultadosposibles
Una canica blanca
Una canica azul
Una canica café
Totales
Si comparamos el valor de la frecuencia relativa del evento ”extraer una canica azul” con
el valor de su probabilidad clásica ¿cuál valor es mayor?
Compara los demás valores y describe qué sucede:
Si la probabilidad de que ocurra un evento es mayor que cero (probabilidad de un evento
nulo) y
menor que 1 (probabilidad de un evento seguro) se dice que es un evento
aleatorio a un caso especial
de un experimento o acción efectuada, como lanzar una
moneda, un dado, sacar una carta, tirar un dardo a la ruleta, etc.
En cambio, a un experimento no aleatorio se le denomina experimento determinístico
Ejemplo: En el diagrama siguiente aparecen marcados los resultados favorables al
evento: “que se obtenga 2 o 3 en alguno de los datos”, del espacio
muestral que corresponde al experimento de “ lanzar dos dados al aire”.
¿Cuántos resultados posibles tiene el evento: que se obtenga 2 o 3 en alguno de los
datos?
¿Qué fracción representa este conjunto del total de resultados posibles del experimento
de lanzar dos dados al aire?
El propósito de la pregunta es que los alumnos identifiquen el evento que tiene mayor
probabilidad clásica (o teórica) de ocurrir. Al lanzar los dados hay 36 resultados posibles,
que corresponde al espacio muestral del experimento de lanzar dos dados; cada uno con
la misma probabilidad de ocurrir. Es posible que, cuando se considera la suma de los
números que se obtienen, los alumnos determinen que hay 11 resultados posibles: 2, 3, 4,
5, 6, 7, 8, 9, 10, 11 y 12; sin embargo, no todos tienen la misma probabilidad de ocurrir
(para la suma 7 hay 6 formas de obtenerla y la suma 2 se obtiene de una sola forma:
cuando cae 1 en ambos dados.).
Pida a estos alumnos que le comenten sobre los resultados posibles hasta completar el
espacio muestral del evento: que sume 2 o 3. Puede ser que estén considerando por
separado el número de resultados en el que se obtiene 2 y en el que cae 3; es decir, que
supongan que en el primer dado hay 6 formas de obtener 2 y 6 cuando cae 3, y que
consideren la misma cantidad de resultados para el segundo dado. La conclusión errónea
sería entonces que existen 24 resultados favorables. Pídales que cuenten los resultados
favorables que se señalan en la retroalimentación, resalte que (3,2) y (3,3) se consideran
solamente una vez.
Aunque en la primaria los alumnos ya han resuelto ejercicios semejantes, es posible que
algunos tengan dificultades para abordarlos, si esto ocurre, hay que promover una
discusión para recordar que la probabilidad de obtener un resultado puede expresarse
con la razón del número de casos favorables entre el número total de resultados posibles.
Algunos problemas un poco más complejos podrían ser los siguientes:

Al realizar el experimento de lanzar simultáneamente dos dados y sumar los puntos
obtenidos:
 ¿Cuál es el espacio muestral de obtener 2 puntos?
 ¿Cuál es el espacio muestral de obtener 10 puntos?
 ¿De cuántas maneras posibles se puede obtener un número mayor que 3 y
menor que 6?
 ¿Qué es más probable, que se obtenga un número par o uno impar? ¿Por
qué?
 ¿Qué es más probable, que se obtenga un número múltiplo de 2, un número
múltiplo de 3 o un múltiplo de 4? ¿Por qué?
 Experimento: Lanzas dos monedas al mismo tiempo y observas las caras que caen.
Obtener el espacio muestral
 Evento R: "En la primera moneda cae sol". ¿Cuántos resultados posibles hay?
 Evento S: "En la segunda moneda cae sol". ¿Cuántos resultados posibles hay?
 Se tiene un disco giratorio dividido en 10 sectores circulares iguales, tres de los cuales
están marcados con 1, dos con 2 y cinco con 3.
 ¿Cuál es la probabilidad de que el dardo se clave en un sector marcado con 1?
 ¿Cuál es la probabilidad de que el dardo se clave en un sector marcado con 2?
 ¿Cuál es la probabilidad de que el dardo se clave en un sector marcado con un
número diferente a 1?
 ¿Qué es más probable, que el dardo se clave en un sector marcado con 1 o en
uno marcado con 3?


Al realizar el experimento de lanzar simultáneamente dos dados y sumar los puntos
obtenidos:
 ¿Cuál es la probabilidad de obtener 2 puntos?
 ¿Cuál es la probabilidad de obtener 10 puntos?
 ¿Cuál es la probabilidad de obtener un número mayor que 3 y menor que 6?
 ¿Qué es más probable, que se obtenga un número par o uno impar? ¿Por
qué?
 ¿Qué es más probable, que se obtenga un número múltiplo de 2, un número
múltiplo de 3 o un múltiplo de 4? ¿Por qué?
Al realizar el experimento de lanzar un dado:
a) ¿Cuál es el espacio muestral?
b) ¿Cuál es la probabilidad de obtener un número mayor que 10? ¿Por qué?
c) ¿Cuál es la probabilidad de obtener un número menor que 7? ¿Por qué?
La intención de las preguntas es que los alumnos descubran que la escala para calcular
la probabilidad clásica va desde 0, es decir desde que el evento es imposible que ocurra,
hasta el 1 cuando es seguro que el evento suceda. Algunas preguntas adicionales que
permiten este análisis son las siguientes:
¿Se podría dar el caso en que el número de resultados favorables sea mayor que el
número de resultados posibles?
¿Cuál es el mayor valor que puede tener la medida de la probabilidad? ¿Y el menor?
¿Qué significa que un fenómeno tiene probabilidad cero de ocurrir?
¿Qué significa que un fenómeno tiene probabilidad uno de ocurrir?
La clave para que el alumno adquiera un aprendizaje significativo tiene que ver con las
preguntas que hagamos al respecto del objeto de estudio y
la reafirmación del
conocimiento adquirido.
Cuando se ha terminado el análisis de las preguntas puede pedírseles que intenten
representar las probabilidades encontradas con otras expresiones equivalentes. Concluir
que la probabilidad puede expresarse con una fracción, con un decimal o con un
porcentaje. Así la respuesta a la pregunta c) es ½, 0.5 o 50%.
2.1 Predicción
Al lanzar dos dados, ¿cuál de los siguientes eventos tiene mayor probabilidad de ocurrir?
a)
b)
c)
d)
Que la suma de los números que salgan sea par
Que se obtenga dos o tres en alguno de los dados
Que la suma de los números que salgan sea menor o igual a 7
Que la suma de los números que salgan sea impar
Es recomendable que se propicie el análisis de las predicciones y compararlas con los
resultados del juego; de ser posible aclarar las confusiones a partir del espacio muestral
del experimento “lanzar dos dados y sumar los puntos que salgan”; así mismo elaborar
el diagrama de árbol o arreglo cartesiano que muestre todas las posibles soluciones y
contrastarlas con los resultados reales al lanzar varias veces dos dados; entendiendo por
“salir”, las caras que quedan hacia arriba en cada dado.
a) Que la suma de los números que salgan sea par
b) Que se obtenga dos o tres en alguno de los dados
c) Que la suma de los números que salgan sea menor o igual a 7
d) Que la suma de los números que salgan sea impar
Es recomendable que se propicie el análisis de las predicciones y compararlas con los
resultados del juego; de ser posible aclarar las confusiones a partir del espacio muestral
del experimento “ la suma de las caras superiores al lanzar dos monedas al aire”, que se
puede representar mediante un diagrama de árbol o arreglo rectangular.
La probabilidad clásica de un evento E, que denotaremos por P(E), se define como el
número de eventos elementales que componen al evento E, entre el número de eventos
elementales que componen el espacio muestral:
Es la definición más utilizada porque supone de antemano, y se necesita como
requisito indispensable, que todos los eventos elementales tienen la misma
probabilidad de ocurrir.
3.1 Eventos independientes o mutuamente excluyentes
Determinar el espacio muestral que resulta al hacer el experimento de lanzar dos dados y
contesten las siguientes preguntas:
a) ¿Cuál es la probabilidad de que los dos dados caigan en número par?
b) ¿Cuál es la probabilidad de que en ambas caras aparezca el mismo número?
c) ¿Cuál es la probabilidad de que la suma de sus caras sea 10?
d) ¿Cuál es la probabilidad de que la suma de sus caras sea un 10 o un 6?
e) ¿Cuál es la probabilidad de que la suma de sus caras sea 10 y en ambas aparezca
el mismo número?
La idea fundamental de esta actividad es retomar elementos básicos de la probabilidad
mediante diversos cálculos.
Un arreglo rectangular o un diagrama de árbol son recursos que, si no surgen
espontáneamente de los alumnos, pueden sugerirse para determinar el espacio muestral
del experimento. Si se considera pertinente puede darse incompleta una de estas
herramientas para que los estudiantes la terminen, por ejemplo el arreglo rectangular
siguiente:
1
1
2
3
4
6
(1,1)
2
(2,5)
3
(3,4)
4
5
5
(4,3)
(5,2)
6
(6,6)
NOTA: Es importante que los alumnos se percaten que en los eventos d y e se están
utilizando conectivos y que para el caso del primero (o) significa que se trata de la
probabilidad de que ocurra cualquiera de dos eventos, mientras que el conectivo y implica
que deben ocurrir ambos eventos a la vez.
Si se presentan las diferentes formas de expresar la probabilidad (fracción, decimal o %),
aprovechar para analizar sus equivalencias y conversiones.
Situación 1. Representa en forma decimal las siguientes situaciones
a) Calcular la probabilidad de obtener 1 y águila al lanzar un dado y una moneda.
b) Calcular la probabilidad de obtener 1 al lanzar el dado, sabiendo que ya salió
águila al lanzar la moneda.
Situación 2. Representa en % la probabilidad de cada evento siguiente
a) ¿Cuál es la probabilidad de obtener un número par y menor que 4 al lanzar un
dado?
b) Sabiendo que ya salió par, ¿cuál es ahora la probabilidad que sea menor que 4?
Igual que en la actividad anterior, las probabilidades pedidas pueden obtenerse a partir de
la determinación del espacio muestral correspondiente. La atención de estas consignas se
centra en identificar la dependencia o independencia de los eventos que se presentan en
cada situación: en la primera se trata de eventos independientes, el resultado de uno no
tiene efecto en el resultado del otro, la probabilidad de obtener 1 al lanzar el dado no
depende del resultado de lanzar la moneda, siempre es 1/6, aún sabiendo que la moneda
ya cayó en águila. En cambio en la segunda situación se trata de eventos dependientes,
la probabilidad de que el número sea menor que 4 es ½ (1, 2 y 3), pero si se sabe que ya
salió par, el espacio muestra se reduce a (2, 4 y 6), de los cuales uno (el 2) es menor que
4, por lo tanto la probabilidad es 2/6 =1/3.
En ocasiones un evento o más eventos dependen de otro evento previo, es decir, un
evento A ocurre dado que ocurrió un evento B. Si existe este tipo de relación entre
eventos se dice que son eventos dependientes o condicionados (A/B) (el evento A
depende del evento B, o el resultado del evento A está condicionado al resultado del
evento B).
Por otro lado, si no existe tal relación entre eventos se dice que son eventos
independientes o mutuamente excluyentes.
Es conveniente que se analicen otras situaciones que incluyan eventos independientes,
algunos ejemplos son:
1. Se lanzan cinco volados consecutivos y en todos ellos ha caído sol. ¿Cuál es la
probabilidad de que en el sexto volado también caiga sol?
2. Se va a realizar una rifa con 200 boletos que han sido numerados del 1 al 200.
Todos los boletos se han vendido. El boleto ganador será el primero que se saque
de una urna. Ana compró los boletos 81, 82, 83 y 84. Juan adquirió los boletos 30,
60, 90 y 120. ¿Quién tiene más oportunidades de ganar?
3. La mamá de Enrique y la Tía de Ana están embarazadas y próximamente darán a
luz a sus bebés. ¿Qué probabilidad hay de que las dos tengan un hijo varón?
4. Se lanzan simultáneamente un dado y una moneda. ¿Cuál es la probabilidad de
que caiga sol y el número 4?
Es muy probable que los alumnos obtengan por separado las probabilidades de cada
evento en cada problema, para el primero ½ y ½ y para el segundo 1/6 y ½; sin embargo
el asunto es averiguar cómo se relacionan estas medidas para obtener la probabilidad de
que ocurran, en cada caso, los dos eventos a la vez, para el primero ¼ y para el segundo
1/12. Un arreglo rectangular o un diagrama de árbol permiten visualizar el espacio
muestral y los casos favorables de cada situación.
Otros problemas que permitirán aplicar la regla encontrada son los siguientes:

Variantes del problema 2.
¿Cuál es la probabilidad de que caiga águila y 2?
¿Cuál es la probabilidad de que caiga sol y 6?
¿Cuál es la probabilidad de que caiga águila y un número mayor que 4?

Pedro y Mario van a extraer sin mirar una canica de una caja que contiene dos
amarillas, una verde y tres rojas. Si después de cada extracción se regresa la
canica a la caja, ¿cuál es la probabilidad de que Mario tome una canica roja y
Pedro una amarilla?
1.2 Características de los eventos mutuamente excluyentes
Las siguientes figuras representan un tetraedro (poliedro regular de cuatro caras) y una
ruleta. En forma individual resuelve los problemas que se plantean y comenta tus
resultados con tres de tus compañeros más cercanos.
1.- Al girar la ruleta, ¿qué probabilidad existe de que la ruleta se detenga en...
a)
b)
c)
d)
el número 5?
un número menor que 4?
un múltiplo de 2?
un número impar?
2.- Si se lanza el tetraedro, ¿cuál es la probabilidad de que la cara que quede sobre la
superficie plana, sea…
a) color rojo?
b) verde o rojo?
c) verde o blanco o rojo?
Es conveniente plantear primero el problema uno y hacer una puesta en común para
analizar los resultados de los cuatro incisos. Debe quedar claro que el espacio muestra en
el experimento de la ruleta es el conjunto {1, 2, 3, 4, 5, 6, 7, 8} y que a cada elemento le
corresponde una probabilidad de 1/8. Con base en esto se podrán contestar las cuatro
preguntas. Si los alumnos preguntan cuáles son los múltiplos de dos hay que decirles que
son todos los resultados de la tabla del dos.
En el segundo problema también conviene destacar el espacio muestra y enfatizar el
hecho de que en los incisos b y c, se trata de eventos compuestos y que los conectivos
“o” indican que se trata de la probabilidad de que suceda cualquiera de los dos o de los
tres eventos, a diferencia del conectivo “y”, que se refiere a la probabilidad de que
sucedan dos o más eventos a la vez. Por lo tanto, la probabilidad en el inciso b) es ¼ + ¼,
mientras que en c) es ¼ + ¼ + ¼.
Si dos eventos son independientes o mutuamente excluyentes, es decir que no ocurren
simultáneamente, entonces la frecuencia relativa de su unión es la suma de las
frecuencias relativas de cada uno.
Propiedad 1. Si A y B son dos eventos, la probabilidad de que ocurra A o B es igual a
la suma de las probabilidades de ocurrencia de A y de B, menos la probabilidad de que
El experimento consiste ahora en girar la ruleta y observar en qué número se detiene.
Con base en esto contesten las siguientes preguntas:
a)
b)
c)
d)
¿Cuál es la probabilidad de que la ruleta se detenga en un número par?
¿Cuál es la probabilidad de que la ruleta se detenga en un número impar?
¿Pueden ocurrir al mismo tiempo los eventos a) y b)?, ¿porqué?
¿Cuál es la probabilidad de que la ruleta se detenga en un número par o
un número impar?
d) ¿Cuál es la probabilidad de que la ruleta se detenga en un número par o
múltiplo de tres?
e) ¿Cuál es la probabilidad de que la ruleta se detenga en un número par y
múltiplo de tres?
(Se hace referencia al tetraedro y ruleta nuevamente).
Se lanza el tetraedro y se hace girar la ruleta simultáneamente, ¿qué probabilidad hay de
que la ruleta se detenga en el número 4 y el tetraedro caiga sobre su color verde?
En la primera consigna es importante discutir y confrontar las respuestas de los incisos d
y f, estableciendo en primer lugar la diferencia entre los conectivos “o” e “ y”. Mientras
que el conectivo o implica que suceda cualquiera de los dos eventos o ambos, el
conectivo y implica la ocurrencia de los dos eventos a la vez. En este caso el único
número que cumple con las dos condiciones (ser número par y a la vez múltiplo de tres)
es el seis, por lo tanto el resultado en el inciso e es 1/8.
El problema de la segunda consigna resultará un poco más difícil para los alumnos
porque el evento compuesto (cuatro y color verde) proviene de dos experimentos distintos
y hay que saber cómo relacionar la probabilidad particular de cada evento: P {caer 4} =
1/8; P {color verde} = ¼. Es probable que algunos alumnos sumen estos valores y
obtendrán 3/8. En tal caso se puede cuestionar: ¿Consideran que la probabilidad de que
ocurran dos sucesos a la vez puede ser mayor que la probabilidad de que ocurra sólo uno
de esos sucesos? Si los alumnos caen en cuenta de que no puede ser, hay que
explicarles que el resultado es el producto de las probabilidades particulares.
Dos eventos A y B son dependientes si y sólo si la Probabilidad del evento A dado que
ocurra B es igual a la probabilidad de A; o bien, La probabilidad de B dado que ocurra A es
igual a la Probabilidad B. o lo que es lo mismo:
P(A|B) = P(A) y P(B|A) = P(B)
Por lo tanto la probabilidad de que ocurra A y B es el producto de las probabilidades de
ambos eventos
P(A  B) = P(A) · P(B)
1. Si se tienen los eventos:
A. Que la ruleta se detenga en un número menor que cuatro.
B. Que se detenga en un número múltiplo de cuatro.
a) ¿Cuál es la probabilidad del evento A? p(A) = ___________
b) ¿Cuál es la probabilidad del evento B? p(B) = ___________
c) ¿Qué significa que ocurra A o B? ___________________________________
d) ¿Qué significa que ocurra A o B? ___________________________________
e) ¿Cuál es la probabilidad de que ocurra A o B? p(A o B) = ______________
f) ¿Cuál es la probabilidad de que ocurra A y B? p( A y B)= ________________
Expliquen su respuesta en cada caso.
2. Ahora se tienen los eventos siguientes:
C. Que la ruleta se detenga en un número mayor que cuatro.
D. Que la ruleta se detenga en un múltiplo de cuatro.
a) Obtengan: p(C) = __________
p(D) = ____________
b) ¿Cuál es la probabilidad de que ocurra C o D? P(C o D) = ____________
3. Comparen los resultados de d) del ejercicio 1 y de b) del ejercicio 2 y comenten las
formas de obtenerlos.
¿Existe alguna diferencia en estos eventos? ¿Cuál?
Es conveniente que siempre que los alumnos calculen la probabilidad de un evento
compuesto obtengan primero el espacio muestra y la probabilidad particular de cada
evento, esto les permitirá apreciar si hay elementos comunes o si no los hay. Si no los hay
ya saben que el resultado es la suma de las probabilidades particulares, si los hay, es
probable que por sí solos concluyan que no se puede contar dos veces el mismo
elemento del espacio muestra.
2. Simulación
Analizar los siguientes experimentos, realizarlos y registrar sus resultados:
a) Lanzar 30 veces un dardo a una ruleta dividida en 10 sectores circulares iguales y
numerados del 1 al 10.
b) Hacer girar una perinola hexagonal (comúnmente llamada toma todo), 80 veces.
c) El lanzamiento de un dado 50 veces.
Es muy probable que los alumnos no entiendan en qué consiste simular los experimentos, en
tal caso el profesor podrá intervenir para dar una idea al respecto, “simular consiste en
explorar el comportamiento de una experiencia aleatoria observando otra experiencia
equivalente, pero más fácil de realizar o de estudiar”.
Ante la dificultad de tener en el momento una ruleta y un dardo, si a los alumnos no se les
ocurre como simular este experimento, se les puede sugerir meter en una bolsa o caja 10
papeles numerados del 1 al 10, extraer uno, registrar el resultado y devolverlo a la bolsa;
realizar 29 extracciones idénticas.
El experimento de la perinola puede simularse de manera semejante al de la ruleta,
únicamente que ahora serían 6 papeles y en cada uno se escribe uno de los seis posibles
resultados (toma uno, toma dos, toma todo, pon uno, pon dos y todos ponen), no olvidar
después de cada extracción, regresar el papel a la caja o bolsa.
Para registrar los resultados de cada experimento puede utilizarse una tabla, como por
ejemplo, para el caso de la perinola:
Un agente comercial sabe que cada vez que visita un cliente tiene 20% de probabilidad de
hacer dos ventas, 50% de probabilidad de hacer sólo una y 30% de no vender nada. Un día
tiene cita con cinco clientes. ¿Cuánto puede esperar ganar ese día si por cada venta que
realiza gana $200.00?
Dado que en la consigna se sugiere la simulación del problema, la dificultad radica en buscar
algún material manipulable que se adapte a las condiciones del problema. Una estrategia de
simulación consiste en colocar en una caja o bolsa dos canicas azules, cinco blancas y tres
rojas. Posteriormente, extraer una a una y al azar cinco canicas (los cinco clientes),
devolviendo cada vez la canica antes de extraer la siguiente (el profesor puede preguntar a
los alumnos por qué es necesario devolver las canicas).
Si sale canica azul, el agente hizo dos ventas y ganó $400.00
Si sale blanca, sólo hizo una venta y ganó $200.00
Si sale roja, no hizo ninguna venta y no ganó.
Una vez que cada equipo obtiene una respuesta, conviene registrarlas en el pizarrón y ver si
alguna se repite más veces. Ésta sería la mejor estimación hecha en el grupo. Es importante
agregar, que si el experimento se repitiera muchas más veces, se llegaría a estimar con
mayor exactitud la cantidad que el agente puede ganar ese día.
3. Evaluación de los aprendizajes
Problemas de Probabilidad.
1. María y Laura idean el siguiente juego: cada una lanza un dado, si en los dos
dados sale el mismo número, gana Laura; si la suma de ambos es 7 gana María; y
en cualquier otro caso hay empate.
a) Calcular la probabilidad de que Laura gane el juego
b) Calcular la probabilidad de que gane María
c) Que probabilidad es mayor; ¿Qué gane cualquiera de las dos o que
empaten?
2. Dos parejas de novios deciden ir al cine. Si se sientan al azar en cuatro butacas
contiguas, ¿cuál es la probabilidad de cada uno esté al lado de su pareja?
3. Una urna A contiene 5 bolas blancas y 4 negras; y otra urna B contiene 1 blanca
y 2 negras. Se extrae una bola al azar de la urna A y se introduce en la B.
Después se extrae de la urna B una bola al azar.
a) Calcular la probabilidad de que la bola extraída de la urna B sea
blanca.
b) Supongamos que la bola extraída de la urna A sea blanca, calcular la
probabilidad de que la extraída de la urna B también sea blanca.
Eventos independientes
4. Los siguientes pares de eventos son independientes, a excepción de uno de ellos.
Identifica cuál es el par de eventos que no son independientes
a) Experimento: Lanzas dos monedas al mismo tiempo y observas las caras
que caen.
Evento R: "En la primera moneda cae sol".
Evento S: "En la segunda moneda cae sol".
b) Experimento: De una bolsa con 5 canicas, en la que 3 son verdes y 2
rojas, sacas primero una canica, anotas su color, la regresas y sacas otra
canica.
Evento R: "En la primera extracción la canica es roja".
Evento V: "En la segunda extracción la canica es verde".
c) Experimento: Lanzas dos veces una moneda y observas la sucesión de
caras obtenidas.
Evento S: "En el primer lanzamiento cae sol".
Evento A: "En el segundo lanzamiento cae águila".
d) Experimento: De una bolsa con 5 canicas, en la que 3 son verdes y 2 rojas,
sacas primero una canica, no la regresas a la bolsa y sacas otra canica.
Evento R: "En la primera extracción, la canica es roja".
Evento V: "En la segunda extracción, la canica es verde".
5. De una bolsa con 5 canicas, en la que 3 son verdes y 2 rojas, sacas primero una
canica, anotas su color, la regresas y sacas otra canica. ¿Cuál es la probabilidad
de que en la primera extracción la canica sea roja y en la segunda, verde?
6. ¿Cuál de los pares de eventos que se definen a continuación son mutuamente
excluyentes?
a) Experimento: Lanzar un dado y observar el número que cae en la cara superior.
Evento S: “Cae un número mayor que 4”.
Evento T: “Cae un número impar”.
b) Experimento: Lanzar un dado y observar el número que cae en la cara superior.
Evento S: “Cae un número mayor que 5 ”.
Evento T: “Cae un número impar”.
c) Experimento: Lanzar un dado y observar el número que cae en la cara superior.
Evento S: “Cae un número mayor que 4”
Evento T: “Cae 6”.
d) Experimento: Extraer al azar una canica de una bolsa que contiene canicas
grandes y chicas en color azul y blanco.
Evento J: “la canica que se extrae es blanca”.
Evento K: “la canica que se extrae es chica”.
7. Dados dos sucesos aleatorios A y B, se sabe que:
(Bc indica complemento del suceso B)
a) ¿Son los sucesos A y B independientes? Argumenta tu respuesta
b) Calcular P( A  B) 
8. En la Urna1 hay 4 bolas blancas, numeradas del 1 al 4 y 2 bola negras,
numeradas del 1 al 2; mientras que en la Urna2 hay 2 bolas blancas numeradas
del 1 al 2 y 4 bolas negras numeradas del 1 al 4. Se extraen al azar dos bolas de
cada urna. Hallar:
(a) La probabilidad de que tengan el mismo número
(b) La probabilidad de que sean del mismo color
9. La probabilidad de que cierto equipo de futbol gane un partido es 0.4 y la de que
pierda es 0.3 ¿Cuál es la probabilidad de que empate?
10. La probabilidad de que un estudiante universitario termine su carrera en los años
establecidos por el plan de estudios es de
suya sin perder ningún año es de
3
y la de que su hermana finalice la
5
2
. Hallar la probabilidad de:
3
a) Ambos terminen sus estudios en los años establecidos
b) Solo el varón los termine en los años fijados
c) Al menos uno de los dos termine en los tiempos establecidos
11. Una urna contiene 3 canicas, una azul (a), una blanca (b) y otra café (c). Después
de revolver las canicas, se extrae una al azar, se anota su color y se regresa a la
urna. El experimento anterior se repitió 20 veces y se obtuvieron los siguientes
resultados:
b) ¿Cuál crees que será el color de la canica que se extraiga la próxima vez y
por qué?
12. Al lanzar dos dados; ¿Cuál de los siguientes eventos tiene mayor probabilidad de
ocurrir?
a)
b)
c)
d)
“Que la suma de los números que salgan sea par”
“Que se obtenga 2 o 3 en alguno de los lados”
“Que la suma de los números que salgan sea menor o igual a 7”
“Que el producto de los números que salga sea par”
13. Los siguientes pares de eventos son independientes, a excepción de uno de ellos.
Identifica cuál es el par de eventos que no es independiente.
a) Experimento: Lanzas dos monedas al mismo tiempo y observas las caras que
caen
Evento R: “En la primera moneda cae sol”
Evento S: “En la segunda moneda cae sol”
b) Experimento: De una bolsa con 5 canicas, en la que 3 son verdes y 2 son
rojas, sacas primero una canica , anotas su color , la regresas y sacas otra
canica.
Evento R: “En la primera extracción la canica es roja”
Evento V: “En la segunda extracción la canica es verde”
c) Experimento: lanzas dos veces una moneda y observas la sucesión de caras
obtenidas.
Evento S: “En el primer lanzamiento cae sol”
Evento R: “En el segundo lanzamiento cae águila”
d) Experimento: De una bolsa con 5 canicas, en la que 3 son verdes y 2 son
rojas, sacas primero una canica , no la regresas y sacas otra canica.
Evento R: “En la primera extracción la canica es roja”
Evento V: “En la segunda extracción la canica es verde”
14. De una bolsa con 5 canicas, en la que 3 son verdes y 2 son rojas, sacas primero
una canica , anotas su color , la regresas y sacas otra canica. ¿Cuál es la
probabilidad de que en la primera extracción la canica sea roja y en la segunda
sea verde?
15. ¿Cuál de los pares de eventos que se presentan a continuación son mutuamente
excluyentes?
a) Experimento: Lanzar un dado y observar el número que cae en la cara superior
Evento P: “Cae un número mayor que 4”
Evento Q: “Cae un número impar”
b) Experimento: Extraer una canica al azar de una bolsa, en la que 3 son verdes
y 2 son rojas
Evento R: “Extraer la canica roja”
Evento V: “Extraer la canica verde”
c) Experimento: Lanzar un dado y observar el número que cae en la cara superior
Evento S: “Cae un número mayor que 4”
Evento T: “Cae seis”
d) Extraer al azar una canica de una bolsa que contiene canicas grandes y
chicas de color azul y blanco
Evento C: “La canica que se extrae es blanca”
Evento D: “La canica que se extrae es chica”
16. Considera el experimento y los eventos que se definen:
Evento S: “Cae un número menor que 4”
Evento T: “Cae un número mayor que 4”
¿Cuál es la probabilidad de que el numero de la cara que cae hacia arriba sea
menor que 4 o sea mayor que 4?
BIBLIOGRAFIA
 Programa de Estudios de Matemáticas SEP. Reforma en Secundaria 2006. Segunda
edición (México 2009)
 Guía Interactiva para Secundaria. (SEP, 2009) Segunda Edición. México 2009
 Planes de clase para la Asignatura de matemáticas. (SEP, DGDC 2006)
 LIBRO DEL MAESTRO. Secundaria. Segunda edición. 2001 (México D.F.)
 Antología para la Reforma en Secundaria. Matemáticas. Programas de Estudio
2006
 Análisis sobre la teoría del estudio de las matemáticas a partir de la resolución
de problemas (Benitez, David, UA de C. 2007)
 Diplomado en Enseñanza de las Matemáticas Centrado en el Desarrollo de
Competencias. Apuntes. (Benitez, 2008) Secretaría de Educación y Cultura de
Coahuila; Saltillo, Coahuila 2008.
 Programa de Estudios de Matemáticas SEP. Reforma en Secundaria 2006. Segunda
edición (México 2009)
 Guía Interactiva para Secundaria. (SEP, 2009) Segunda Edición. México 2009
 Planes de clase para la Asignatura de matemáticas. (SEP, DGDC 2006)
 LIBRO DEL MAESTRO. Secundaria. Segunda edición. 2001 (México D.F.)
 Antología para la Reforma en Secundaria. Matemáticas. Programas de Estudio
2006
 Análisis sobre la teoría del estudio de las matemáticas a partir de la resolución
de problemas (Benitez, David, UA de C. 2007)
 Diplomado en Enseñanza de las Matemáticas Centrado en el Desarrollo de
Competencias. Apuntes. (Benitez, 2008) Secretaría de Educación y Cultura de
Coahuila; Saltillo, Coahuila 2008.
 Libro Apuntes para la enseñanza.- Matemática. Cálculo mental con números
racionales, propuesto por el Gobierno de la Ciudad de Buenos Aires, Secretaría de
Educación, Dirección General de Planeamiento, Dirección de Curricular.
 Materiales de Apoyo para la Práctica Educativa (MAPE), “ Los decimales: más que
escritura” ; editado por el INEE
 Programa de estudios 2006. Matemáticas. SEP, 2006. México D.F.
 Libro de sexto año, Secuencias Didácticas para el Profesor editado por la
secretaría de Educación pública, 2009.
 “Lee, piensa, decide y aprende” desarrollado por la Dirección General de
Educación Indígena y La Dirección General de Materiales Educativos de la
Subsecretaría de Educación Básica, edición 2010.
 Antología de Matemáticas para la Reforma de Secundaria, editado por la
Secretaría de Educación Pública, 2006.
 Apuntes para la enseñanza.- Matemática. Cálculo mental con números naturales,
propuesto por el Gobierno de la Ciudad de Buenos Aires, Secretaría de
Educación, Dirección General de Planeamiento, Dirección de Curricula.
 Página de internet
www.ditutor.com/numeros_naturales/jerarquia_operaciones.html
 Página de internet www.disfrutalasmatematicas.com/algebra/exponentesleyes.html
 “El papel de la geometría como herramienta para la didáctica de la matemática”
Eduardo Mancera Martínez. Comité Interamericano de Educación Matemática,
México. 2005
 Libro para el Maestro. Matemáticas. SEP, 1997. México, D.F.

http:// www.redescolar.ilce.sep.gob.mx

http://www.profesorenlinea.cl/matematica/Proporcionalidad.htm

http://www.es.wikipedia.org/wiki/Proporcionalidad


http://www.enlace.sep.gob.mx
http://www.emathematics.net/es/

http://www.uaq.mx/matematicas/estadistica