RAZONES Y PROPORCIONES (267934)

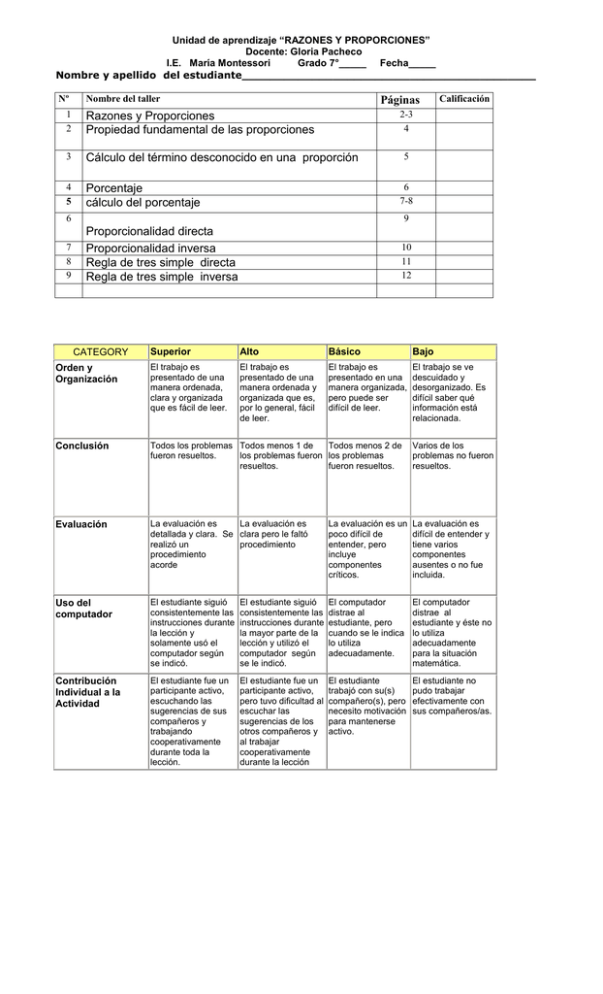
Unidad de aprendizaje “RAZONES Y PROPORCIONES”
Docente: Gloria Pacheco
I.E. María Montessori
Grado 7°_____ Fecha_____
Nombre y apellido del estudiante__________________________________________
Nº
Nombre del taller
Páginas
1
2
Razones y Proporciones
Propiedad fundamental de las proporciones
3
Cálculo del término desconocido en una proporción
4
5
Porcentaje
cálculo del porcentaje
2-3
4
5
6
7-8
6
7
8
9
Calificación
9
Proporcionalidad directa
Proporcionalidad inversa
Regla de tres simple directa
Regla de tres simple inversa
10
11
12
Superior
Alto
Básico
Bajo
Orden y
Organización
El trabajo es
presentado de una
manera ordenada,
clara y organizada
que es fácil de leer.
El trabajo es
presentado de una
manera ordenada y
organizada que es,
por lo general, fácil
de leer.
El trabajo es
presentado en una
manera organizada,
pero puede ser
difícil de leer.
El trabajo se ve
descuidado y
desorganizado. Es
difícil saber qué
información está
relacionada.
Conclusión
Todos los problemas Todos menos 1 de
Todos menos 2 de
fueron resueltos.
los problemas fueron los problemas
resueltos.
fueron resueltos.
Varios de los
problemas no fueron
resueltos.
Evaluación
La evaluación es
La evaluación es
detallada y clara. Se clara pero le faltó
realizó un
procedimiento
procedimiento
acorde
La evaluación es un
poco difícil de
entender, pero
incluye
componentes
críticos.
La evaluación es
difícil de entender y
tiene varios
componentes
ausentes o no fue
incluida.
Uso del
computador
El estudiante siguió
consistentemente las
instrucciones durante
la lección y
solamente usó el
computador según
se indicó.
El estudiante siguió
consistentemente las
instrucciones durante
la mayor parte de la
lección y utilizó el
computador según
se le indicó.
El computador
distrae al
estudiante, pero
cuando se le indica
lo utiliza
adecuadamente.
El computador
distrae al
estudiante y éste no
lo utiliza
adecuadamente
para la situación
matemática.
Contribución
Individual a la
Actividad
El estudiante fue un
participante activo,
escuchando las
sugerencias de sus
compañeros y
trabajando
cooperativamente
durante toda la
lección.
El estudiante fue un
participante activo,
pero tuvo dificultad al
escuchar las
sugerencias de los
otros compañeros y
al trabajar
cooperativamente
durante la lección
El estudiante
trabajó con su(s)
compañero(s), pero
necesito motivación
para mantenerse
activo.
El estudiante no
pudo trabajar
efectivamente con
sus compañeros/as.
CATEGORY
Unidad de aprendizaje “RAZONES Y PROPORCIONES”
Docente: Gloria Pacheco
I.E. María Montessori
Grado 7°_____ Fecha_____
Nombre y apellido del estudiante__________________________________________
TITULO. RAZONES Y PROPORCIONES
OBJETIVOS.
 Reconocer una razón
 Reconocer una proporción
 Diferenciar una razón de una proporción
Conocimientos Previos: Amplificación y simplificación de fracciones
Conceptos:
Actividad 1:
1.
Si te dicen la razón entre los goles del equipo A y el equipo B es de 3 a 1.¿Qué entiendes?
2.
Razón es una expresión que se utiliza tanto en matemáticas como en otras actividades. Escribe tres frases donde
utilices la palabra razón con diferentes significados.
La razón entre dos magnitudes es un número, sin unidades, y se expresa con la división indicada de las magnitudes;
esta división se puede efectuar y su cociente expresa la razón entre las magnitudes.
Ejemplo 1: Las apuestas favorecen al campeón en razón de 6 a 1. Se escribe
6
1
Ejemplo 2: Una sala tiene 8m de largo y 5m de ancho; la razón entre el largo y el ancho es de 8 a 5. Se escribe
8
5
Ejercicios 1:
1.
Un jugador en 21 partidos anotó 7 goles. ¿Cuál es la razón entre el número de goles y los partidos anotados?
2.
En unas elecciones el candidato A obtuvo 120000 votos y el candidato B obtuvo 240000. ¿Cuál es la razón entre
los votos de A y de B?
3.
Para dibujar el croquis de una ciudad se utilizó una escala 1:5000 ¿Qué significa esta expresión?
Actividad 2:
1.
1
2
10
30
3
4
Observe las siguientes razones y escriba entre ellas = si son iguales y
Amplificación y Simplificación de fracciones.

si son diferentes. Para ello recuerde
2
4
1
3
7
5
Al igualar dos razones se obtiene Una PROPORCIÓN.
En una PROPORCIÓN intervienen dos razones; cada razón consta de dos términos: Antecedente y Consecuente.
En la razón
a
, a se llama antecedente y b se llama consecuente
b
En la proporción
a c

el antecedente de la razón de la izquierda y el consecuente de la razón de la derecha se llaman
b d
extremos de la proporción: a y d son los extremos. El consecuente de la razón de la izquierda y el antecedente de la
razón de la derecha se llaman medios de la proporción: b y c son medios.
La proporción
a c

se lee “a es a b como c es a d”; también se escribe a:b::c:d
b d
Unidad de aprendizaje “RAZONES Y PROPORCIONES”
Docente: Gloria Pacheco
I.E. María Montessori
Grado 7°_____ Fecha_____
Nombre y apellido del estudiante__________________________________________
Ejercicios 2:
p
¿Cuál es el antecedente? ¿cuál es el consecuente?
q
1.
En la razón
2.
¿Qué nombre recibe la igualdad de dos razones?
3.
En la proporción
4.
Escribe 5 ejemplos de razones matemáticas y escríbelas en forma simbólica
p r
identifica los medios y los extremos

q s
LOS ÍNTEGROS, LOS PERFECTOS HABITARÁN LA TIERRA Y PERMANECERÁN EN ELLA.
Proverbios 2: 21
Gep/14
Unidad de aprendizaje “RAZONES Y PROPORCIONES”
Docente: Gloria Pacheco
I.E. María Montessori
Grado 7°_____ Fecha_____
Nombre y apellido del estudiante__________________________________________
Tema. PROPIEDAD FUNDAMENTAL DE LAS PROPORCIONES
OBJETIVOS.
 Reconocer la propiedad fundamental de las proporciones
Conocimientos Previos: Concepto de proporción
Conceptos:
Actividad 1
1. ¿Compare las siguientes razones
10
30
1
Son iguales?
3
2. Se puede decir que en el punto 1 ¿existe una proporción?
3. Multiplique los extremos y multiplique los medios. ¿Son iguales los dos resultados?
PROPIEDAD FUNDAMENTAL DE LAS PROPORCIONES: En toda proporción el producto de los medios es
igual al producto de os extremos.
Ejemplo 1: Comprueba que
Solución: Como
4.8

a c
 , entonces a.d  b.c
b d
5 3
 es una proporción.
15 9
Solución: Como 5 . 9 = 15 . 3
Ejemplo 2: Comprueba que
Si
Simbólicamente:
es decir
45 = 45 entonces
5 3

es una proporción
15 9
4 3

no es una proporción
5 8
5.3
es decir 32

15 entonces
4 3

no es proporción
5 8
Ejercicios :
1.
Verifica si las siguientes expresiones son proporciones
5 10

6 12
5
4
b.

4
5
4 10
c.

10 25
a.
2.
9 18

2 4
25 5
e.

24 4
10 1
f.

100 10
d.
g.
h.
i.
1 7

7 1
8 32

9 36
7 1

21 3
Escribe 5 proporciones
“QUE LA AMABILIDAD DE USTEDES SEA CONOCIDA DE TODAS LAS PERSONAS”
Filipenses 4:5
Gep/14
Unidad de aprendizaje “RAZONES Y PROPORCIONES”
Docente: Gloria Pacheco
I.E. María Montessori
Grado 7°_____ Fecha_____
Nombre y apellido del estudiante__________________________________________
Tema. CÁLCULO DEL TÉRMINO DESCONOCIDO EN UNA PROPORCIÓN
OBJETIVOS.
 Aplicar la propiedad fundamental de las proporciones para hallar el valor de una incógnita
Conocimientos Previos: Ecuaciones, Propiedad fundamental de las proporciones
Conceptos:
Cálculo del término desconocido de una proporción: Utilizando la propiedad fundamental de las proporciones se puede
hallar el término desconocido en una proporción así:
Ejemplo 1: Calcula el término desconocido en la proporción:
5 30

x 12
Solución:
5 30

P roporcióndada
x 12
5.12  30.x P ropiedadfundament al de las proporciones
60  30x
Se desarrollael producto
60 30

x
Se aplica propiedadde las ecuacionesmultiplicativas
30 30
2x
Se simplifica
Rta: x=2
Ejemplo 2: Calcula el término desconocido en la proporción:
x 4

7 28
Solución:
x 4

7 28
28x  7.4
28x  28
28x 28

28 28
x 1
P roporcióndada
P ropiedadfundamental de las proporciones
Se desarrollael producto
Se aplica propiedadde las ecuacionesmultiplicativas
Se simplifica
Ejercicios :
1.
a.
d.
g.
Calcula el término desconocido en las siguientes proporciones
5
x

6
12
5
10

x
4
b.
e.
x
18

2
4
25
x

50
4
c.
f.
49
7

7
x
x
4

9
6
Plantea 5 ejercicios y resuélvelos
SI ANDUVIERE YO EN MEDIO DE LA ANGUSTIA, TÚ ME VIVIFICARÁS; CONTRA LA IRA DE MIS
ENEMIGOS EXTENDERÁS TU MANO, Y ME SALVARÁ TU DIESTRA.
Salmo 138:7
Gep/14
Unidad de aprendizaje “RAZONES Y PROPORCIONES”
Docente: Gloria Pacheco
I.E. María Montessori
Grado 7°_____ Fecha_____
Nombre y apellido del estudiante__________________________________________
Tema. PORCENTAJE
Objetivos.
 Reconocer el concepto de porcentaje
Conocimientos Previos: Propiedad fundamental de las proporciones
Actividad 1:
1. Qué significan estas frases de uso común
a. El costo de la canasta familiar aumentó en un 15 por ciento
b. El banco presta dinero al 4 % mensual
c. El incremento salarial este año será del 5 por ciento
d. La utilización del medicamento tal garantiza la mejoría en un 85 %
El PORCENTAJE es una razón muy especial en la cual el segundo término o consecuente es 100, así 15 por ciento
significa quince de cada 100 y se escribe 15%, se lee 15 por ciento, su razón es
15
y su expresión decimal es 0,15.
100
Actividad 2:
1.
Escriba en forma de razón, y como número decimal cada una de las expresiones de la actividad 1.
2.
Escribe los siguientes decimales como fracción y simbolízalos como porcentaje.
3.
a.
0,53
b.
3,47
c.
0,001
d.
2,18
Dadas las siguientes fracciones decimales, escríbelas en forma decimal y simbolízalas como porcentaje.
5
100
10
b.
100
4
c.
100
50
d.
100
a.
4.
Escribe cuatro expresiones que utilicen porcentaje y exprésalas como decimal y como fracción
“PIENSEN EN TODO LO VERDADERO, TODO LO HONESTO, TODO LO JUSTO, TODO LO PURO, TODO
LO AMABLE, TODO LO QUE ES DE BUEN NOMBRE.
Filipenses 4:8
Gep/14
Unidad de aprendizaje “RAZONES Y PROPORCIONES”
Docente: Gloria Pacheco
I.E. María Montessori
Grado 7°_____ Fecha_____
Nombre y apellido del estudiante__________________________________________
Tema. CÁLCULO DEL PORCENTAJE
Objetivos.
 Resolver problemas que utilicen porcentaje
Conocimientos Previos: Propiedad fundamental de las proporciones
Actividad 1:
CÁLCULO DEL TANTO POR CIENTO. Los ejercicios, problemas y cualquier situación donde
intervienen los porcentajes se pueden reducir a uno de los siguientes cálculos.
1. Hallar el tanto por ciento de un número
2. Dados dos números, calcular qué tanto por ciento es uno del otro
3. Hallar un número, del cual se conoce un porcentaje
En el porcentaje intervienen dos magnitudes, una llamada base, que equivale a 100 y la otra llamada
porcentaje, que representa la fracción que se toma de 100.
Veamos con un ejemplo las tres situaciones presentadas anteriormente:
1.
Santiago entra en un almacén a comprar un Jean. Si el pantalón cuesta $25.000. Le
descuentan el 10%. ¿Cuánto dinero es el descuento?
Solución:
10
x

100 25.000
10).(25.000) = 100X
250.000 = 100X
Propiedad fundamental de las proporciones
X = 2.500
Rta: El descuento es de $2.500.
Actividad 1:
Resuelva:
a. Un vestido cuesta $20.000. Si descuentan el 10 %. ¿Cuánto dinero descuentan?
b. Una persona ganaba $462.000. Si le suben el 8%. ¿Cuánto es el aumento?
c. Plantee y resuelva 3 problemas de este tipo
2.
Santiago entra en un almacén a comprar un Jean. Si el pantalón vale $25.000 y le
descuentan $2.500. ¿Qué porcentaje le descuentan?
Solución:
x
2.500

100 25.000
25.000X = (2.500)(100)
25.000 X = 250.000
Propiedad fundamental de las proporciones
Unidad de aprendizaje “RAZONES Y PROPORCIONES”
Docente: Gloria Pacheco
I.E. María Montessori
Grado 7°_____ Fecha_____
Nombre y apellido del estudiante__________________________________________
X = 10
Rta: El descuento es del 10%.
Actividad 2: Resuelva:
a. A una camiseta de $30.000 le descuentan $4.500. ¿Qué porcentaje descontaron?
b. Por cada $300.000 que retiro en el cajero del banco me cobran $2.500. ¿Qué porcentaje me
descuentan?
c. Plantee y resuelva 3 problemas de este tipo
3.
Santiago entra en un almacén a comprar un Jean. Le descuentan el 10% que equivale a
$2.500. ¿Cuál era el precio del pantalón?
Solución:
10 2.500

100
x
10X= (100)(2.500)
10X = 250.000
Propiedad fundamental de las proporciones
X = 25.000
Rta: El pantalón tenía un precio de $25.000.
Actividad 3: Resuelva:
a. El 20% de un libro es de $6.000. ¿Cuál es el precio del libro?
b. El salario mínimo subió un 4% que equivale a $25.000. ¿Cuánto es el salario mínimo?
c. Plantee y resuelva 3 problemas de este tipo
PORQUE DIOS TRAERÁ TODA OBRA A JUICIO, JUNTAMENTE CON TODA
COSA ENCUBIERTA, SEA BUENA O SEA MALA
Eclesiastés 12:14
Gep/14
Unidad de aprendizaje “RAZONES Y PROPORCIONES”
Docente: Gloria Pacheco
I.E. María Montessori
Grado 7°_____ Fecha_____
Nombre y apellido del estudiante__________________________________________
TEMA: PROPORCIONALIDAD DIRECTA
OBJETIVO: Reconocer cuando dos variables son directamente proporcionales
Conocimientos previos: Plano cartesiano
Concepto:
Ejemplo 1: La distancia recorrida por un automóvil y el tiempo gastado están dados en la siguiente tabla:
Distancia
(Km)
Tiempo
(horas)
15
30
45
60
75
90
1
2
3
4
5
6
1. Observamos que intervienen dos variables: Distancia medida en Kilómetros y Tiempo medido
en horas. La distancia depende del tiempo por tanto la distancia es una variable dependiente y
el tiempo es una variable independiente.
2. Analizamos que a medida que aumenta el tiempo aumenta la distancia.
3. Dividiendo la variable dependiente (Distancia) entre la variable independiente (Tiempo) notamos que se
produce un resultado que es constante:
15
 15,
1
4.
30
 15,
2
45
 15,
3
60
 15,
4
75
 15,
5
90
 15,
6
Al realizar la gráfica se obtiene una recta que pasa por el origen.
En conclusión:
Dos Variables son directamente proporcionales cuando:
1. Al aumentar una variable, aumenta la otra
2. El cociente entre la variable dependiente y la variable independiente es constante.
3. La gráfica es una recta que pasa por el origen.
Actividad 1:
1. Dada la relación entre el precio de una camiseta y el número de ellas consignado en la siguiente tabla:
Nº de
4
8
12
16
20
24
camisetas
Precio
40.000
80.000
120.000
160.000
200.000
240.000
Comprobar si la relación entre el número de camisetas y el precio es directamente proporcional.
2.
Diseñe una tabla de datos cuyas variables sean directamente proporcionales
“POR NADA ESTÉN AFANADOS, SINO SEAN CONOCIDAS TODAS SUS
NECESIDADES DELANTE DE DIOS EN ORACIÓN Y RUEGO, CON ACCIÓN DE
GRACIAS”
Filipenses 4:6
Gep/14
Unidad de aprendizaje “RAZONES Y PROPORCIONES”
Docente: Gloria Pacheco
I.E. María Montessori
Grado 7°_____ Fecha_____
Nombre y apellido del estudiante__________________________________________
OBJETIVO: Reconocer cuando dos variables son inversamente proporcionales
Conocimientos previos: Plano cartesiano
Concepto:
Comprenderemos este concepto a través de un ejemplo
Ejemplo : La velocidad de un móvil y el tiempo gastado están dados en la siguiente tabla:
Velocidad
(Metros/segundo)
Tiempo(segundos)
2.
3.
4.
25
50
100
200
400
800
64
32
16
8
4
2
1. Ob
servamos que intervienen dos variables: Velocidad medida en metros/segundo y Tiempo
medido en segundos. La velocidad depende del tiempo por tanto la velocidad es una
variable dependiente y el tiempo es una variable independiente.
Analizamos que a medida que aumenta la velocidad disminuye el tiempo.
Multiplicando la variable dependiente (Velocidad) por la variable independiente (Tiempo) notamos que
se produce un resultado que es constante:
25 x 64 = 1600,
50 x 32 = 1600,
100 x 16 =
1600,
400 x 4 = 1600,
800 x 2 = 1600
Al realizar la gráfica se obtiene una curva llamada hipérbola.
En conclusión:
Dos Variables son inversamente proporcionales cuando:
1. Al aumentar una variable, la otra disminuye
2. El producto entre la variable dependiente y la variable independiente es constante.
3. La gráfica es una gráfica llamada hipérbola.
Actividad 2:
1. Dada la relación entre el número de obreros y el tiempo que tardan en realizar una obra está dado en la siguiente
tabla:
Nº de obreros
2
4
8
10
40
Tiempo (Días) 100
50
25
20
5
Comprobar si la relación entre el número de obreros y el tiempo que tardan en realizar la obra es inversamente
proporcional.
2.
Diseñe una tabla de datos cuyas variables sean inversamente proporcionales
“DIGA EL DÉBIL, FUERTE SOY”
Joel 3:10
Gep/14
Unidad de aprendizaje “RAZONES Y PROPORCIONES”
Docente: Gloria Pacheco
I.E. María Montessori
Grado 7°_____ Fecha_____
Nombre y apellido del estudiante__________________________________________
TEMA: REGLA DE TRES SIMPLE DIRECTA
OBJETIVO: Resolver problemas de regla de tres simple directa
Conocimientos previos: Propiedad fundamental de las proporciones, proporcionalidad directa.
Concepto:
La regla de tres simple es un método para resolver problemas en los que intervienen dos magnitudes
proporcionales.
REGLA DE TRES DIRECTA: Si las magnitudes que intervienen son directamente proporcionales.
Ejemplo: Un auto, por cada 100 Km de recorrido, consume 5 galones de combustible. ¿Cuántos kilómetros
ha recorrido dicho auto si el consumo de combustible es de 25 galones?
Solución:
Observamos que a más distancia recorrida mayor será el gasto de combustible, las variables que
intervienen son distancia (Medida en kilómetros) y combustible (Medido en galones). La relación entre
las variables es directa.
Distancia
(Kilómetros)
Combustible
(Nº Galones)
x
100
x
5
25
100 x 25
 500
5
Como la relación es directa entonces existe un cociente
constante entre las variables, luego tenemos la igualdad
100
x

5
25
Se aplica la propiedad fundamental de las proporciones para hallar el valor de x
RTA: Recorre 500 Km.
Resuelve los siguientes problemas:
1) Un carpintero elabora 5 sillas durante 6 días. ¿Cuántas sillas construirá en 12 días?
2) Si 5 cuadernos tienen un precio total de $1.700, ¿cuál será el costo de 16 cuadernos?
3) Si un poste de alumbrado eléctrico, que tiene 14 m de altura, proyecta una sombra de 7m, ¿cuál será la
sombra proyectada por una persona que mide 1.70 metros?
4) Si un automóvil recorre 600 Km en 7 horas, ¿cuántas horas tardará en recorrer 900 Km, si la velocidad del
automóvil es constante?
5) Los 3/5 de la capacidad de un estanque equivalen a 150 galones. ¿Cuántos galones equivalen a los 2/5 de
dicho estanque?
6) Plantee
y resuelva 5 problemas de regla de tres simple directa
EL NECIO AL PUNTO DA A CONOCER SU IRA; MÁS EL QUE NO HACE CASO DE
LA INJURIA ES PRUDENTE.
Proverbios 12:16
Gep/14
Unidad de aprendizaje “RAZONES Y PROPORCIONES”
Docente: Gloria Pacheco
I.E. María Montessori
Grado 7°_____ Fecha_____
Nombre y apellido del estudiante__________________________________________
TEMA: REGLA DE TRES SIMPLE INVERSA
OBJETIVO: Resolver problemas de regla de tres simple inversa.
Conocimientos previos: Propiedad fundamental de las proporciones, proporcionalidad inversa.
RECORDAR: La regla de tres simple es un método para resolver problemas en los que intervienen dos
magnitudes proporcionales.
REGLA DE TRES INVERSA: si las magnitudes que intervienen son inversamente proporcionales.
Ejemplo: Tres pintores de brocha gorda pintan una casa en 6 días. ¿Cuántos días demorarán 9 pintores en
pintar la misma casa?
Solución:
Observamos que a más pintores menor es el tiempo que tardan en hacer la obra. Las variables que
intervienen son Nº de pintores y el tiempo (medido en días). La relación entre las variables es inversa.
Pintores
Días
x
3x6
2
9
3
6
9
x
Como la relación es inversa entonces existe un producto constante
entre las dos variables luego tenemos la igualdad (3) .(6) = 9.x
Se despeja la x aplicando propiedades de las ecuaciones
RTA: Demoran 2 días
Resuelve los siguientes problemas:
1. Seis obreros hacen una zanja en 8 días. ¿Cuántos días tardarán 12 obreros en hacer una zanja igual?
2.
Una pared tiene 6 m de longitud por 3.5 m de alto.¿Cuál será el largo de una pared de 7 m de alto y la
misma superficie que la anterior?
3.
15 obreros pavimentan una calle en 20 días. ¿Cuántos obreros hacen falta para pavimentar la misma calle
en 10 días?
4.
5.
6.
Si 5 carpinteros fabrican un galpón en 9 días, ¿cuantos días emplearán 3 carpinteros?
¿Qué dimensiones hay que variarle a una puerta, si tiene 1.90 m de alto por 0,70 m de ancho, para que,
conservando la misma superficie, su altura sea de 1.70 m?
Plantee y resuelva 3 problemas de regla de tres simple inversa
“DIOS ES EL QUE DA LA SABIDURÍA, Y DE SU BOCA VIENE EL CONOCIMIENTO Y LA
INTELIGENCIA”.
Proverbios 2:6
Gep/06
Unidad de aprendizaje “RAZONES Y PROPORCIONES”
Docente: Gloria Pacheco
I.E. María Montessori
Grado 7°_____ Fecha_____
Nombre y apellido del estudiante__________________________________________
Marque la respuesta y realice el procedimiento
1.
Cuál de las siguientes equivalencias es una
proporción
1
3
4
b.
8
6
c.
5
3
d.
4
a.
2
5
1
9
12
10
30
20
m
2. El antecedente en la razón
es:
n
a.
m
b.
m
n
c.
d.
0
n
1
10

3. Los extremos en la proporción
3
30
a.
b.
c.
d.
son respectivamente:
1 y 3
1 y 30
1 y 10
3 y 10
x 9

4. El valor de X en la proporción
es:
2 6
a.
b.
c.
d.
6
3
9
2
5.
5 % equivale a la razón
5
100
5
b.
10
100
c.
5
5%
d.
10
a.
6.
a.
b.
c.
d.
43 % equivale al decimal
74,3
43,0
0,043
0,43
7.
El 10% de es el descuento por comprar con
tarjeta en un supermercado. Si compro $25.000
El descuento es:
500
25000
2500
250
a.
b.
c.
d.
8.
b.
c.
d.
e.
9.
a.
b.
c.
d.
A una camiseta de $14800 se le descuenta el
20%. ¿En cuánto queda?
$ 11740
$ 2860
$ 11840
$ 1480
El 7 % de descuento de un play es $4200. ¿Cuál
era el precio?
600000
60000
6000
600
10. Si unos tenis de $50000 los rebajaron a
$25.000 ¿qué porcentaje descontaron?
a.
b.
c.
d.
50%
25%
30%
10%
¡EXITOS!
Gep/06
Y SI ALGUNO DE USTEDES TIENE FALTA
DE SABIDURÍA, PÍDALA A DIOS, EL CUAL
DA A TODOS ABUNDANTEMENTE Y SIN
REPROCHE, Y LE SERÁ DADA.
Santiago 1:5
Marque la respuesta y realice el procedimiento
Las preguntas 1 a la 5 se resuelven con base en el
siguiente problema.
Pedro recorre 13 Km en 2 días. Si mantiene la misma
velocidad, ¿Cuántos Km recorrerá en 9 días?
1. Las variables que intervienen en el anterior
problema son:
a. Días y tiempo
b. Distancia y tiempo
c. Nº de obreros y tiempo
d. Kilómetros y distancia
2. La relación que existe entre las variables es:
Unidad de aprendizaje “RAZONES Y PROPORCIONES”
Docente: Gloria Pacheco
I.E. María Montessori
Grado 7°_____ Fecha_____
Nombre y apellido del estudiante__________________________________________
a.
b.
c.
d.
Inversa
Ninguna
Directa
Todas
3. La regla de tres que se aplica para solucionar el
anterior problema es:
a. Inversa
b. Directa
c. Ninguna
d. Todas
4. Los Km que recorre Pedro en 9 días son:
a. 117 Km
b. 18
Km
c. 13
Km
d. 58,5 Km
Los puntos 5 al 8 se resuelven con base en el siguiente
problema:
Dos obreros pintan una casa en dos semanas,
trabajando 4 horas diarias. Si se mantiene el mismo
ritmo de trabajo, ¿Cuántos obreros se necesitan para
terminar el trabajo en 1 semana?
5. Las variables que intervienen en el anterior
problema son:
a. Obreros y horas
b. Tiempo y Horas
c. Tiempo y Nº de obreros
d. Días y semanas
6.
a.
b.
c.
d.
La relación que existe entre las variables es:
Inversa
Ninguna
Directa
Todas
7. La regla de tres que se aplica para solucionar el
anterior problema es:
a. Inversa
b. Ninguna
c. Directa
d. Todas
8. Los obreros que se necesitan para terminar el
trabajo en una semana son:
a. 1 obreros
b. 3 semanas
c. 2 obreros
d. 4 obrero
Los puntos 9 y 10 se resuelven con base en el
siguiente problema
Si compro una camiseta de $18000 me descuentan
el 15%.
9. El descuento es de:
a. $ 1800
b. $ 14400
c. $ 3600
d. $ 18000
10.
a.
b.
c.
d.
El nuevo precio de la camiseta será:
$ 1800
$ 14400
$ 3600
$ 18000
Unidad de aprendizaje “RAZONES Y PROPORCIONES”
Docente: Gloria Pacheco
I.E. María Montessori
Grado 7°_____ Fecha_____
Nombre y apellido del
estudiante__________________________________________
Y SI ALGUNO DE USTEDES TIENE FALTA DE SABIDURÍA, PÍDALA A
DIOS, EL CUAL DA A TODOS ABUNDANTEMENTE Y SIN REPROCHE, Y
LE SERÁ DADA.
Santiago 1:5
¡EXITOS!
Gep/06