Observadores en Modos Deslizantes

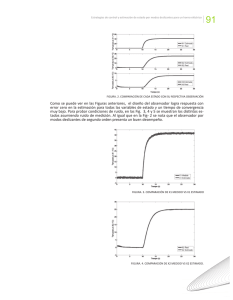
OBSERVADORES EN MODOS DESLIZANTES
CAPITULO SEIS
Observadores en Modos Deslizantes
Todos los métodos de diseño de los capítulos anteriores, excepto de aquellos de la
sección 5.5, se han desarrollo en el espacio de estado. En la práctica, sin embargo,
solo una parte de las componentes pueden ser medidas directamente. Los métodos de
control en modos deslizantes de la sección 5.5 (con la señal de salida siempre
disponible para la retroalimentación) son aplicables solo a un número limitado de
sistemas. Una alternativa es diseñar observadores asintóticos, los cuales constituyen
modelos dinámicos para estimar todas las componentes del vector de estado
utilizando la medición directa de las componentes. Primeramente, se estudiarán los
observadores convencionales de orden completo y de orden reducido relacionados
con sistemas lineales e invariantes con el tiempo. Posteriormente se presentarán las
modificaciones a modos deslizantes de los observadores de estado de sistemas
variantes e invariantes en el tiempo (Utkin, 1992) con estimación de perturbaciones
externas (Hashimoto et al., 1990).
6.1 Observadores lineales.
La idea de diseño de los observadores puede ser ilustrada para sistemas invariantes
en el tiempo (5.1.1.):
•
x = Ax + Bu
(6.1.1)
con el vector de salida
y = Cx
y ∈ℜl ,
C = const ,
rank (C ) = l
(6.1.2)
La pareja de matrices (C,A) se suponen observables.
Un observador lineal se diseña en la misma forma que el sistema original
(6.1.1) con una entrada adicional pendiente de la diferencia entre los valores reales
(6.1.2) y los valores estimados del vector de salida:
•
xˆ = Axˆ + Bu + L(Cxˆ − y)
(6.1.3)
OBSERVADORES EN MODOS DESLIZANTES
Donde x̂ es un estimado del vector de estado del sistema y L ∈ ℜ n× l es una
matriz de entrada. Por supuesto, el vector del observador de estado x̂ está disponible
para generar la acción de control con ayuda de la dinámica del sistema auxiliar.
La ecuación del movimiento con respecto a la diferencia x = xˆ − x es:
•
x = ( A + LC ) x
(6.1.4)
El comportamiento del corrimiento gobernado por la ecuación homogénea (6.1.4)
se determina mediante los valores característicos de al matriz A + CL . Para los
sistemas que sean observables, es posible seleccionar en forma arbitraria a la matriz L
(Kwakernaak y Sivan, 1972). Esto significa que es posible prever cualquier razón de
convergencia de la matriz de estado. Por lo tanto, es posible aplicar cualquier
algoritmo de control utilizando el estado observado xˆ (t ) .
El orden del observador puede reducirse debido al factor de rango de rango(C ) = l
y el vector de estado puede ser representado como:
y = C1 x1 + C 2 x2
[
x T = x1T
]
xT2 ,
x1 ∈ ℜ n −1 , x2 ∈ ℜ1 , del (C 2 ) ≠ 0
Es suficiente diseñar el observador para el vector x1 , siendo el valor de x 2 igual a:
x 2 = C 2−1 ( y − C1 x 1 )
(6.1.5)
Escribiendo las ecuaciones del sistema (6.1.1),(6.1.2) en el espacio ( x1 , y) :
•
x1 = A11 x1 + A12 y + B1 u
•
y = A21 x1 + A22 y + B2 u
 A11
TAT −1 = 
 A21
Donde
(6.1.6)
A12 
A22 
 B1 
TB =  
 B2 
I n −l
T=
 C1
0
C 2 
(Si la transformación de coordenadas es no singular, entonces det( T ) ≠ 0 .)
El diseño de observadores de orden reducido se basa en la transformación de
coordenadas
x′ = x1 + L1 y
(6.1.7)
y el comportamiento del sistema se considera en el espacio ( x ′ , y ) . Obvia mente, la
transformación
de coordenadas para cualquier L1 es no singular.
La ecuación con respecto a x′ se obtiene de (6.1.5) hasta (6.1.7):
•
′ y + ( B1 + L1 B 2 )u
x′ = ( A11 + L1 A21 ) x′ + A12
A12′ = A12 + L1 A22 − ( A11 + L1 A21 ) L1
OBSERVADORES EN MODOS DESLIZANTES
El observador se diseña en la forma de un sistema dinámico de orden (n − l )
•
′
xˆ ′ = ( A11 + L1 A21 ) xˆ′ + A12 y + (B1 + L1 B 2 )u
(6.1.8)
Siendo xˆ ′ como un estimado del vector de estado x′ , la diferencia x ′ = xˆ ′ − x′ esta
regida por la ecuación:
•
x ′ = ( A11 + L1 A21 ) x ′
(6.1.9)
Si el sistema original es observable, la matriz de valores característicos
A11 + L1 A21 puede ser asignada arbitrariamente (Kwakernaak and Sivan, 1972). Esto
significa que x ′ tiende a cero y xˆ ′ tiende a x′ para cualquier razón deseada. Las
componentes del vector de estado x1 , y x 2 , se encuentran en (6.1.5) y (6.1.7).
6.2 Observadores para sistemas lineales e invariantes con el tiempo
A continuación se procede con el diseño de observadores de estado con funciones
discontinuas como entradas de diferencias donde el movimiento precede a los modos
deslizantes puede ser manejada en la intersección de la superficie discontinua. El
observador es descrito mediante las ecuaciones diferenciales:
•
xˆ1 = A11 xˆ1 + A12 yˆ + L1 v
•
yˆ = A21 xˆ1 + A22 yˆ + B2 u − v
(6.2.1)
donde x̂1 e ŷ son los valores estimados del sistema,
v = Msign( yˆ − y)
M > 0,
M = constante
Si el vector “y” esta disponible para su medición, e s posible obtener el valor de yˆ − y .
El vector de función discontinua v ∈ ℜ l se selecciona con el propósito de que
los modos deslizantes obliguen a que el vector de diferencia y = yˆ − y tienda a cero.
La matriz L1 debe seleccionarse a fin de que la diferencia x1 = xˆ1 − x1 tienda a cero
con una velocidad específica. Las ecuaciones para x1 y y se obtienen de las
ecuaciones (6.1.6) y (6.2.1):
•
x1 = A11 x1 + A12 y + L1 v
y = A21 x1 + A22 y − v
v = Msign ( y )
(6.2.2)
Como se mostró en la sección 2.4, los modos deslizantes obligan a la ecuación
de diferencia a reducirse a cero ( y = 0 ) si la matriz multiplicadora v en la segunda
ecuación de (6.2.2) es definida negativa y M toma valores finitos pero muy grandes.
Este es el caso, debido a que v es multiplicada por una matriz identidad negativa. Es
posible que los modos deslizantes obliguen a la ecuación diferencia y = 0 tienda a
cero siempre y cuando las condiciones iniciales esten acotadas. Recordando los
OBSERVADORES EN MODOS DESLIZANTES
•
métodos de control equivalente para obtener v eq y resolver la ecuación y = 0 es
necesario primeramente sustituir con y = 0 en la ecuación (6.2.2) para derivar la
ecuación en modos deslizantes:
v eq = A21 x1
•
x1 = ( A11 + L 1 A21 ) x1
(6.2.3)
Lo cual coincida con la expresión (6.1.9). Seleccionando apropiadamente el
valor de L es posible la convergencia de las variables x1 → 0 y xˆ1 → x1 y
posteriormente es posible obtener x 2 mediante la expresión (6.1.5).
El observador en modos deslizantes con una función discontinua como entrada
(6.2.2) es equivalente a un observador de orden reducido (6.1.8). Sin embargo, si una
señal de ruido afecta tanto a la planta como al observador, es preferible un obse rvador
no lineal debido a sus propiedades de filtrado, que coinciden en su forma de operar
con los filtros de Kalman (Drakunov, 1983).
6.3 Observadores para sistemas lineales variantes en el tiempo
6.3.1 Esquema del observador
Para los sistemas variante s en el tiempo:
•
x = A(t ) x + B (t )u
(6.3.1)
y = C (t ) x
(6.3.2)
donde x ∈ ℜ n , u ∈ ℜ m e
y ∈ ℜ l , siendo el vector de salida y (t ) y las matrices
A(t ), B (t ) y C (t ) conocidas. Se pretende diseñar un observador que estime al vector
de estado x(t) .
Para cualquier transformación no sinusoidal del estado x en ( y T0 , x1T ),
y0 ∈ ℜ l0 , x1 ∈ ℜ n −l 0 , la ecuación (6.3.1) esta representada mediante:
•
∗
y0 = A00 (t ) y0 + A01
(t ) x1 + B0 (t )u
(6.3.3)
•
x1 = A10∗ (t ) y0 + A11∗ (t ) x1 + B1∗ (t )u
(6.3.4)
El sistema en (6.3.3), (6.3.4) para un vector y0 conocido se conoce como modelo
Bloque -Observador. Los índices y superíndices en (6.3.3), (6.3.4) denotan los bloques
matriciales. El sistema (6.3.3), (6.3.4) puede ser representado en modo BloqueObservador si el rango de l 0 y la posición del menor principal de la matriz C(t) no varia
con el tiempo. En este paso, después de ordenar los vectores x e y , existe una matriz
Λ 0 (t ) tamaño (l − l 0 ) × l 0 tal que:
OBSERVADORES EN MODOS DESLIZANTES
 C 0 (t ) 
C (t ) = 

Λ 0 (t )C0 (t )
(rangoC0 (t ) = l 0 )
y la matriz C0 de tamaño l 0 × n es de la forma:
[
C0 (t ) = C o/ (t ) C 0// (t )
]
Siendo la matriz C 0// (t ) de tamaño l o × l 0 no singular. El vector y0 se obtiene como:
y 0 = C 0 (t ) x = C 0/ (t ) x 1 + C 0// (t ) x 1∗
[
donde x T = x1T
]
[
x1∗ se transforma en y 0T
/
 y0 
 x1   C0
 x  = T0  x∗  =  I
 1
 1   n −l 0
x1T
]
C 0//   x1 

0   x1∗ 
(det(T0 ) ≠ 0)
La ecuación de salida (6.3.2) esta escrita como:
 C0 
 C 0  x1   y0   I l0 
y=
x=

 ∗  = 
 =   y0
Λ 0 C 0 
Λ 0 C 0  x1  Λ 0 y0  Λ 0 
(6.3.5)
Donde I l 0 es una matriz identidad. El vector y 0 consiste de elementos linealmente
independientes del vector y , por lo tanto el sistema puede ser transformado en un
Bloque -Observador usando la expresión (6.3.5).
Este procedimiento permite formar un Bloque-Observador para 0 < l0 < n . En
el caso en que l 0 = 0 implica que el sistema original no es observable (bajo la
suposición de que la posición del menor principal no varíe con el tiempo). Para
l 0 = n es posible obtener el vector de estado directamente de la expresión y = C (t ) x .
∗
Tomando l vector A01
(t ) x1 en el bloque (6.3.3) como un vector de salida del
subsistema (6.3.4) y suponiendo que la posición y el rango del menor principal de la
∗
matriz A01
(t ) no varia con el tiempo, el subsistema (6.3.3) puede ser representado en
∗
la forma de un Bloque-Observador. El rango de A01
(t ) es igual a l1 ( 0 ≤ l1 ≤ l 0 ) . Existe
una matriz Λ1 (t ) de tamaño (l 0 − l1 ) × l1 tal que:
 C1 (t ) 
∗
A01
(t ) = 

Λ1 (t )C1 (t )
rangoA01∗ (t ) = l1
[
rangoC1 (t ) = l1
]
C1 (t ) = C1/ (t ) C1// (t )
(det_ C1// (t ) ≠ 0)
donde C1/ (t ) ∈ ℜ l1×( n −l0 −l1 ) , C1// (t ) ∈ ℜ l1×l1 . Entonces y1 (t ) esta dada por
OBSERVADORES EN MODOS DESLIZANTES
y1 (t ) = C1 (t ) x1 = C1/ (t ) x 2 + C1// (t ) x ∗2
donde y1 ∈ ℜl1 , x2 ∈ ℜ n−l 0 −l1 y x2∗ ∈ ℜ l1 ,
 y1 
x  =
 2
 C1/

I n −l1 −l 0
C1//   x2 
 x2 
  ∗  = T1  ∗ 
0   x2 
 x2 
(det_(T1 ) ≠ 0 )
Aplicando esta transformación al sistema (6.3.4), se obtiene la siguiente ecuación:
•
•
y 
 y•1  = T1 A10∗ y0 + (T1 A11∗ T1−1 + T1 T1−1 )  1  + T1 B1∗ u
x 
 x2 
 2
(6.3.6)
donde
•
A
(T1 A11∗ T1−1 + T1 T1−1 ) =  11
∗
 A21
 A10 
∗
T1 A10
= ∗
 A20 
A12∗ 
∗ 
A22

B 
T1 B1∗ =  1∗ 
B 2 
La ecuación (6.3.6) se escribe como:
•
y1 = A10 (t ) y0 + A11 (t ) y1 + A12∗ (t ) x 2 + B1 (t )u
•
∗
∗
x2 = A∗20 (t ) y 0 + A21
(t ) y1 + A22
(t ) x2 + B 2∗ (t )u
El bloque (6.3.3) se escribe como:
•
y0 = A00 (t ) y0 + A01 (t ) y1 + B0 (t )u
(6.3.7)
 Il 
A01 (t ) =  1 
Λ 1 (t )
donde
(rango _ A01 (t ) = l1
Para l1 < n − l0 el sistema (6.3.7) también puede ser representado en forma de
un Bloque-Observador ( l1 > 0, de otra forma el sistema en (6.3.1), (6.3.2) no es
observable). Después de cada paso, la dimensión de x i es menor que la dimensión de
xi −1 , por lo que el procedimiento termina después de un número finito de pasos.
Observando que el procedimiento de diseño del Bloque-Observador del i-ésimo
sistema es:
•
i
yi = ∑ Ai , j (t ) y j + Ai∗, j +1 (t ) xi +1 + Bi (t )u
j =0
•
i
∗
∗
∗
xi +1 = ∑ Ai , j (t ) y j + Ai +1,i +1 (t ) xi +1 + Bi +1 (t)u
j =0
(6.3.8)
OBSERVADORES EN MODOS DESLIZANTES
el rango y la posición del menor principal de la matriz Ai∗,i +1 (t ) no varia con el tiempo.
Finalmente, este procedimiento termina después de r pasos y y r = C r x r = C r// x ∗r +1
( xr +1 = 0) .
•
yr = Ar 0 (t ) y 0 + Ar 1 (t ) y1 + ... + Arr (t ) yr + Ar∗, r +1 (t ) xr +1 + B r u
r
= ∑ Ar , j (t ) y j + B r (t )u
j =0
De forma semejante a (6.3.3) y (6.3.7), Ai*,i +1 (t ) xi +1 en (6.3.8) puede ser
reemplazado mediante Ai ,i +1 (t ) yi +1 como se muestra a continuación:
•
yi = Ai (t ) yi∗ + Ai ,i +1 (t ) yi +1 + Bi (t )u
(i = 1,..., r − 1)
(6.3.9)
•
yr = Ar (t ) yr∗ + Br (t )u
(6.3.10)
donde Ai (t ) = ( Ai 1 , Ai 2 ,..., Aii ), yi∗T = ( yT0 , y1T ,..., yiT ), yi ∈ ℜ li , rango _ Ai ,i +1 (t ) = l i +1 y
Ai ,i +1 es una matriz completa en rango. Por lo tanto, los sistemas (6.3.9), (6.3.10)
estan representados mediante el siguiente formato para Bloque-Observador:
 y0 
y 
 1
d y2 
 =
dt  ... 
 ... 
 
 y r 
 A00
A
 10
 A20

 ...
 ...

 Ar 0
A01
0
0
...
A11
A12
0
...
A21
...
A22
...
A23 ...
... ...
...
Ar 1
...
Ar 2
...
Ar 3
...
...
0   y 0  B0 
0   y1   B1 
0   y 2  B2 
   +  u
...   ...   ... 
Ar −1, r   ...   ... 
   
Arr   yr  B r 
con matrices Ai ,i =1 completas en rango.
6.3.2 Diseño de Observadores
Utilizando el enfoque en modos deslizantes, el procedimiento de diseño de
observadores para sistemas variantes en el tiempo puede ser dividido en r problemas
independientes de estabilización, todos ellos triviales.
Sea la ecuación del observador este en la forma:
•
yˆ i = Ai (t ) yˆ i∗ + A i ,i +1 (t ) yˆ i +1 + Bi (t )u + v i
•
yˆ r = Ar (t ) yˆ ∗r + B r (t )u + v r
(i = 0 ,..., r − 1)
(6.3.11)
OBSERVADORES EN MODOS DESLIZANTES
Las señales de entrada v i para el observador se diseñan mediante:
v0 = M 0 sign( y 0 − yˆ 0 )
(6.3.13)
•
vi = M i sign( Ai+−1,i z i )
τ i zi + zi = vi −1
(i = 0 ,..., r )
(6.3.14)
Donde la seudomatriz de la izquierda Ai+−1,i ( Ai+−1,i Ai −1, i = I l i ) existe, debido a que Ai+−1,i
es una matriz de rango completo. La ecuación de diferencia ~y i = y i − yˆ i es:
 y0 
y 
 1
d y2 
 =
dt  ... 
 ... 
 
 y r 
 A00
A
 10
 A20

 ...
 ...

 Ar 0
A01
0
0
...
A11
A12
0
...
A21
...
A22
...
A23 ...
... ...
...
Ar 1
...
Ar 2
...
Ar 3
...
...
0   y 0  v 0 
0   y1   v1 
0   y 2  v 2 
   +  u
...   ...   ... 
Ar −1,r   ...   ... 
   
Arr   y r  vr 
Estando las condiciones iniciales acotadas, para cualquier valor finito
M 1 ,..., M r existe un número ( M 0 ) tal que después de un intervalo de tiempo finito, se
presentan los modos deslizantes cerca de la trayectoria y 0 = 0 dado que cada
componente de y0 y su derivada con respecto al tiempo tiene diferentes signos (2.4.1).
•
De acuerdo con el método de control equivalente (sección 2.3), la solución de y 0 = 0
junto con y0 = 0 ,
(v0 ) eq = ( M 0 sing ( y0 )) eq = A01 y1
Deberá ser sustituido en (6.3.14) para obtener la ecuación en modos
deslizantes. Por lo tanto la señal de salida del filtro de primer orden z1 se aproxima al
valor de la señal de entrada del control equivalente v 0 eq :
lim
τ1 → 0
z1 = v0 eq = A01 y1
De forma semejante,
y
y1 =
lim
τ1 → 0
A01+ z1
y2 puede obtenerse desde el segundo bloque
(subsistema con respecto a y1 ).
y2 =
lim
τ2 → 0
A12+ z2
Consecuentemente, los modos deslizantes acontecen en cada bloque, y
entonces todos los subvectores y1 ,..., y r convergerán a cero. Debido a que
OBSERVADORES EN MODOS DESLIZANTES
y i = yˆ i + y i (i = 1,..., r ) todos los subvectores de los vectores de estado ( y1 ,..., y r )
incluyendo x podrán ser calculados.
Comentarios 6.1
1.- El procedimiento es invariante con respecto a
matrices Ai (t ) de tamaño
li × (li + ... + l i ) para i=0,...,r.
2.- No es obligatorio el uso de los modos deslizantes en el último bloque debido a que:
v r −1, eq = Ar −1,r (t ) y r
y los últimos subvectores yr pueden obtenerse mediante:
yr = yˆ r + Ar+−1, r (t ) z r
3.- Cuando exista un vector de perturb aciones desconocido f(t) en el último bloque,
•
yr = Ar (t ) y r + Br (t )u + f (t )
f (t ) ∈ ℜ lr
la ecuación de diferencia está en la forma
•
yr = Ar (t ) y r + f (t ) − vr
Después de presentarse los modos deslizantes en el subsistema, yr = 0 y
v req = f (t )
y
lim
τf →0
z f = v req = f (t )
•
si
τ f z f + z f = vr .
Como se esperaba, el último bloque permite la obtención del vector de perturbaciones
desconocido el cual incluye perturbaciones externas, variaciones en los parámetros y
funciones de estado no lineales. Este concepto se explica en el capítulo 8 como uno
de los métodos de supresión de chattering.
6.3.3 Resultados de la simulación
Como ejemplo ilustrativo del diseño de observadores, considere el siguiente
sistema variante en el tiempo:
•
x = A(t ) x + B (t )u + f (t )
y = C (t ) x
donde
OBSERVADORES EN MODOS DESLIZANTES
a 00
 0
A(t ) = 
a 20

 0
a 01
a 03 
0 
a 23 

a33 
C00
C (t ) = 
 0
C01 0 0
C11 0 0
0
a 11 a12
0
0
a 31 0
b 00 0 
0 b 
11 
B(t ) = 
0
0


0
0
f (t ) = [0 0
f2
f3 ]
Los elementos de las matrices coeficientes, las entradas y las perturbaciones
son como se indica a continuación:
a00 = −4e − t
a01 = −2 + sin (t / 2)
a 11 = −5 cos(0 .3t )
a 23 = −2 e − t
t+2
t +1
a 31 = −1 −
a 33 = −2
a03 = a12 = a20 = − 1
b00 = −3
b11 = −5e −t / 5
c 00 = 4 + sin (t / 2)
c10 = 2 − e − t / 5
c11 = −5 + 0 .5 sin (−0 .3t )
u1 = −3
u 0 = 5 cos t
Para la matriz de salida C(t)
c
rango 00
0
c01 
=2
c11 
t ∈ [0 , ∞)
El rango y la posición del menor principal de la matriz C(t) no varia con el
tiempo.
El esquema Bloque -Observador se puede obtener fácilmente siguiendo el
método descrito en este capítulo:
d  y0 
 =
dt  y1 
 A00
A
 10
A01   y 0   B0 
0 
+  u +  



A11   y1   B1 
f
donde
c00 c01   x1 
y0 = 
 
 0 c11  x 2 
OBSERVADORES EN MODOS DESLIZANTES
x 
y1 =  3 
 x4 
Los observadores, (6.3.11) hasta (6.3.14), tienen la forma:
d  yˆ 0 
 =
dt  yˆ1 
 A00
A
 10
A01   yˆ 0  B0 
v 0 
+  u +  



A11   yˆ 1   B1 
 v1 
donde v0 y v1 son entradas al observador:
v0 = M 0 sign( y 0 − yˆ 0 )
v1 = M 1 sign( A01−1 z1 )
•
τ 1 z1 + z1 (t ) = v0 (t )
z1 (0) = 0
La simulación se ejecuto para dos casos.
Sistema sin perturbaciones
Los valores iniciales del estado del estado están dados por:
x 0 (0) = x1 (0 ) = x 2 (0) = x 3 ( 0) = 5
Debido a que las perturbaciones se suponen igual a cero, solo se considera la
estimación del estado. Los valores iniciales del observador de estado son iguales a
cero.
Debido a que el intervalo de muestreo T s define la frecuencia de conmutacion,
la constante del filtro τ 1 , la cual debe teóricamente acercarse a cero, se selecciona
como 4Ts . El intervalo de muestreo se selecciona para 100 µs . La figura 6.1 describe
los estados x2 (t ),
x 3 (t ) y las salidas xˆ 2 (t ), xˆ 3 (t ) del observador en modos
deslizantes. Observe como los estados estimados convergen rápidamente a los
valores reales. Nuevamente las matrices M 0 y M 1 son:
5 0 
M0 = 

0 5 
10 0 
M1 = 

 0 10 
OBSERVADORES EN MODOS DESLIZANTES
(a)
(b)
Figura 6.1 Valores para (a) Los valores de los estados reales x 2 (t ) y x 3 (t ) , y (b) la salida
del observador en modos deslizantes xˆ 2 (t ) y xˆ3 (t ) .
Sistema con perturbaciones
Debido a que las señales de perturbaciones f 2 , f 3 necesitan ser estimadas, es necesario
introducir un filtro adicional (comentario 6.1 , punto 3):
•
τ f z f + z f (t ) = v1 (t )
z f (0 ) = [0 0 ]T
Las perturbaciones estimadas a la salida del filtro son:
fˆ (t ) = z f (t )
[
fˆ (t ) T = fˆ2 (t )
fˆ3 (t )
]
La constante de tiempo τ 1 se selecciona en 500 µs . Las condiciones de simulación son las
mismas que en el caso 1. La estimación de la respuesta en la figura 6.2 demuestra que las
perturbaciones desconocidas pueden obtenerse mediante los observadores en modos
deslizantes.
(a)
(b)
Figura 6.2 Perturbaciones: (a) real, (b) estimado.
OBSERVADORES EN MODOS DESLIZANTES
Referencias bibliográficas
Drakunov, S., 1983, On adaptive quasioptical filter with discontinuous parameters, Automation and
remote Control, 44, 1167-75.
Hashimoto, H. et al., 1990, VSS observer for linear time-varying system, Proceedings of IECON’90,
Pacific Grove CA, pp.34-39.
Kwakernaak, H. and Sivan, R., 1972, Linear Optimal Control System, New York: Interscience.
Utkin, V., 1992, Sliding modes in Control and Optimization, Berlin: Springer-Ve
OBSERVADORES EN MODOS DESLIZANTES