Práctico 12c

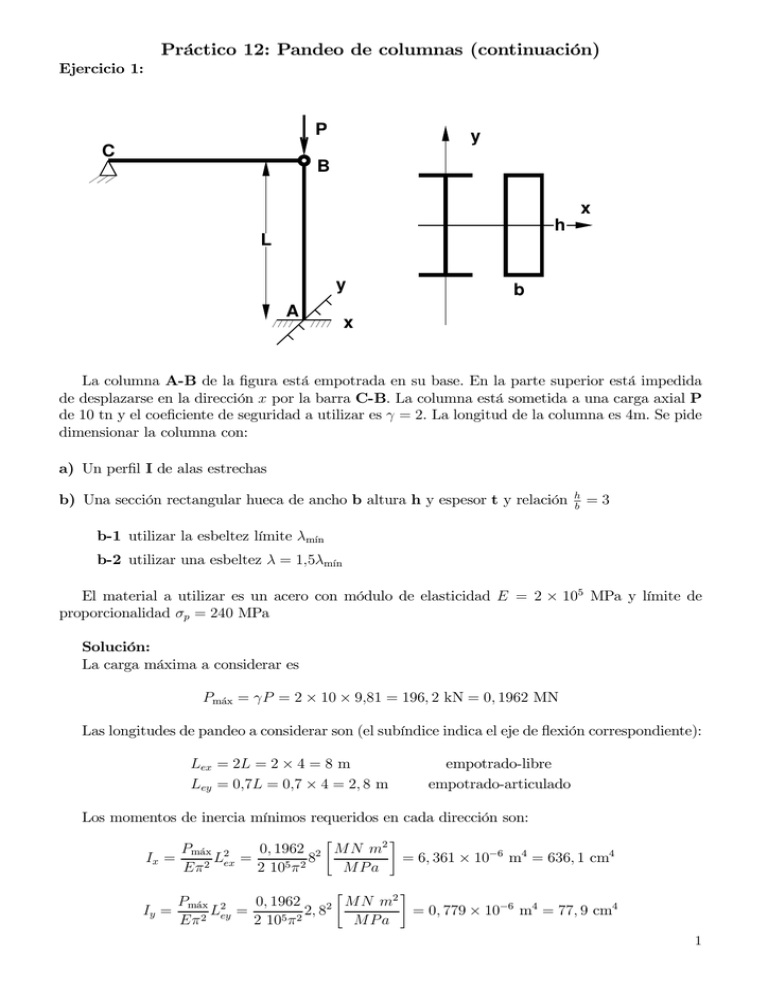
Práctico 12: Pandeo de columnas (continuación)
Ejercicio 1:
P
C
y
B
x
h
L
y
A
b
x
La columna A-B de la figura está empotrada en su base. En la parte superior está impedida
de desplazarse en la dirección x por la barra C-B. La columna está sometida a una carga axial P
de 10 tn y el coeficiente de seguridad a utilizar es γ = 2. La longitud de la columna es 4m. Se pide
dimensionar la columna con:
a) Un perfil I de alas estrechas
b) Una sección rectangular hueca de ancho b altura h y espesor t y relación
h
b
=3
b-1 utilizar la esbeltez límite λmı́n
b-2 utilizar una esbeltez λ = 1,5λmı́n
El material a utilizar es un acero con módulo de elasticidad E = 2 × 105 MPa y límite de
proporcionalidad σp = 240 MPa
Solución:
La carga máxima a considerar es
Pmáx = γP = 2 × 10 × 9,81 = 196, 2 kN = 0, 1962 MN
Las longitudes de pandeo a considerar son (el subíndice indica el eje de flexión correspondiente):
Lex = 2L = 2 × 4 = 8 m
Ley = 0,7L = 0,7 × 4 = 2, 8 m
empotrado-libre
empotrado-articulado
Los momentos de inercia mínimos requeridos en cada dirección son:
Pmáx 2
0, 1962 2 M N m2
= 6, 361 × 10−6 m4 = 636, 1 cm4
L =
8
Ix =
Eπ2 ex 2 105 π 2
MPa
2
Pmáx 2
0, 1962
2 MN m
Iy =
L =
2, 8
= 0, 779 × 10−6 m4 = 77, 9 cm4
Eπ 2 ey 2 105 π 2
MPa
1
La relación entre estos momentos de inercia mínimos en cada dirección es igual a la relación
entre los cuadrados de las longitudes equivalentes de pandeo
L2
636, 1
Ix
= ex
=
≃ 8, 15
Iy
77, 9
L2ey
La esbeltez límite es
λmı́n = π
E
=π
σp
2 × 105
= 90, 7
240
a) dimensionado con un perfil I de alas estrechas.
Entrando en la tabla se busca un perfil que satisfaga los valores pedidos para Ix e Iy . El primer
perfil que satisface es el de 180 mm de altura que tiene
Ix = 1450 cm4 >> 636, 1 cm4
Iy = 81, 3 cm4 > 77, 9 cm4
Claramente la dirección más comprometida es la dirección de flexión alrededor de y (plano
x − z) . Notar que este tipo de perfiles tiene una muy alta relación entre los momentos de inercia
en una y otra dirección IIxy = 17, 83. A pesar de que la longitud de pandeo en el plano y − z es
mucho mayor, el tipo de perfil utilizado conduce a un dimensionado según la flexión en el plano
x − z.
La tensión crítica y las esbelteces en cada dirección resultan (A = 27, 9 cm2 , rx = 7, 20 cm y
ry = 1, 71 cm)
0, 1962
MN
Pmáx
σC =
=
= 70, 32 MPa
A
27, 9 × 10−4 m2
Lex
800
= 111, 1
=
λx =
rx
7, 2
E
Ley
280
λy =
= 163, 7 = π
=
ry
1, 71
σC
b) dimensionado con una sección rectangular hueca:
El área de la sección es:
8
h
+ h = th
A = 2t (b + h) = 2t
3
3
Los momentos de inercia son (despreciando términos en t3 )1 :
3
1 2
1
1 1
h
3
Ix = t 2 + bh = th
+
= th3
12 2
6 6
3
3
2 3
1
1 2
1
1
b
5
th3
Iy = t 2 + b h = th3 3 +
=
12 2
6
2 3
81
La relación entre los momentos de inercia es
Ix
1 81
= 5, 4
=
Iy
3 5
esta relación es menor que 8, 15 por lo cual la dirección de flexión crítica es la x (plano y − z).
1
2
ver al final
Los radios de inercia en cada dirección son:
1 th3 3
h2
Ix
=
=
A
3 th 8
8
3
Iy
5
5 th 3
5 2
ry2 =
=
=
h = b2
A
81 th 8
216
24
rx2 =
b-1: λ = λmı́n
De la expresión λ2 =
L2ex
rx2
despejamos rx2 y de allí obtenemos h
2
L2ex
8002 240
800
L2 σp
= 2 =
= e2 = 2
= 77, 81cm2
λmı́n
90, 7
π E
π 2 105
h2 = 8rx2 = 8 × 77, 81cm2 = 623 cm2
h = 25 cm
rx2
El espesor se obtiene usando que la tensión crítica es igual a la tensión de proporcionalidad
Pmáx
A
0, 1962 MN
8
Pmáx
=
A=
= 8,175 cm2 = th
σp
240
MPa
3
3A
3 8, 175
t=
=
= 0,125 cm = 1, 25 mm
8h
8 25
σp =
El espesor t resultante es muy delgado y puede dar a lugar a problemas de inestabilidad local.
Este diseño guíado por la condición de mínima cantidad de material requiere en este caso de
verificaciones de otro tipo (fuera del alcance de esta asignatura).
b-2: λ = 1, 5 λmı́n = 136
Si utilizamos una relación de esbeltez más elevada, equivalente a disminuir la tensión crítica a:
λmı́n 2
240
σc = σp
=
= 106, 7 MPa
λ
(1, 5)2
se tiene ahora
L2ex
8002
=
= 34, 6cm2
λ2
1362
h2 = 8rx2 = 8 × 34, 6cm2 = 277 cm2
h = 16, 7 cm
rx2 =
El area se obtiene de que la tensión crítica es igual 106, 7
Pmáx
A
0, 1962 MN
λ 2
Pmáx
=
) × Amı́n
A=
= 18, 39 cm2 = (
σc
106, 7 MPa
λmı́n
σc =
y el espesor resulta
8
A = th
3
3 18, 39
3A
=
= 0, 413 cm = 4, 13 mm
t=
8h
8 16, 7
3
Ejercicio 2:
e
P
y
x
h
b
b
Una columna de 3,5 m de altura está empotrada en su base y libre en su extremo superior.
La columna es de acero (E = 2, 06 105 MPa y σp = 230 MPa.) y su sección está formada por
dos perfiles U del 18 enfrentados. a) Si la columna está sometida a una carga axial P = 30
tn, determinar las máximas excentricidades en ambas direcciones de tal forma que el material se
mantenga en estado elástico. b) Si la excentricidad es e = 5cm en la flexión alrededor del eje x,
determinar la máxima carga sin que el material entre en fluencia.
Solución:
Las propiedades básicas del perfil individual son:
Area
28 cm2
Ix
1350 cm4
Iy
114 cm4
h
b
ey
rx
ry
180 mm 7,0 cm 1,92 cm 6,95 cm 2,02 cm
La principal propiedad a determinar del perfil compuesto es el momento de inercia en la dirección y y el radio de giro
Iycompuesto = 2 Iy + A × (b − ey )2 = 1673 cm4
compuesto
I
1673
y
rycompuesto =
=
= 5, 46
compuesto
A
56
Luego las propiedades de la sección son:
Area
56 cm2
Ix
2700 cm4
Iy
1673 cm4
h
2b
rx
ry
180 mm 140 mm 6,95 cm 5,46 cm
Las cargas críticas en ambas direcciones son:
π 2 EIx
π 2 2, 06 1011 2700 10−8 Pa m4
=
=
= 1, 12 MN
m2
(2L)2
(2 3, 50)2
π 2 EIy
π 2 2, 06 1011 1673 10−8 Pa m4
C
=
= 0, 694 MN
Py =
m2
(2L)2
(2 3, 50)2
PxC
4
a) (P = 30 tn = 0, 294 MN) En cada dirección la relación entre la carga actuante y la carga
crítica es
0, 294
0, 294
= 0, 2625
Py∗ =
= 0, 4236
Px∗ =
1, 12
0, 694
La tensión máxima de compresión según la fórmula de la secante es
π √ A
|σ|máx = σ0 1 + e sec
P∗
W
2
Despejamos de la fórmula de la secante e
π √ W
σp
cos
−1
P∗
e=
σ0
A
2
donde
0, 294 MN
P
=
σ0 =
= 52, 5 MPa
A
0, 0056 m2
r2
6, 952
Wx
= x =
= 5, 37 cm
A
h/2
9
σp
230
− 1 = 3, 38
−1 =
σ0
52, 5
ry2
Wy
5, 462
=
=
= 4, 26 cm
A
b
7
Para las distintas direcciones se tiene:
π 0, 2625 = 12, 58 cm
ex = 3, 38 5, 37 cm cos
2
π
ey = 3, 38 4, 26 cm cos
0, 4236 = 7, 51 cm
2
Notar que estas excentricidades máximas se han calculado en forma independiente, es decir
suponiendo que no hay excentricidad en la otra dirección.
Los máximos momentos de extremo asociados exclusivamente a las excentricidades son
Mx0 = P ex = 30 × 12, 58 tn cm = 377, 4 tn cm = 37, 0 kN m
My0 = P ey = 30 × 7, 51 tn cm = 225, 3 tn cm = 22, 1 kN m
Los máximos momentos que se producen en el empotramiento debido a las excentricidades más
los desplazamientos se obtienen de la expresión
Mmáx =
y resultan respectivamente
Mx
máx
My
máx
Mo
√
cos π2 P ∗
37
π√
kN m = 53, 4 kN m
cos 2 0, 2625
22, 1
π√
kN m = 42, 39 kN m
=
cos 2 0, 4236
=
Naturalmente debieran coincidir las tensiones debidas a flexión σf = σp − σ0 = 230 − 52, 5 =
177, 5 MPa
Mx máx
My máx
≃
≃ σf
Wx
Wy
9
7
kN m
≃ 177, 5 MPa
53, 4
≃ 42, 39
2700
1673
cm3
5
b) e = 5cm. En la fórmula de la secante
π √ A
P∗
|σ|máx = σ0 1 + e sec
W
2
buscamos el valor de P que conduzca al valor |σ|máx = σp . Damos valores a todo lo conocido (P
en MN):
5
P
π
P
1+
240 MPa =
sec
0, 0056 m2
5, 37
2 1, 12 MN
No es posible despejar P , por lo cual es necesario evaluarlo en forma iterativa (por ej. el Método
de Newton-Raphson):


0, 931
 − 1, 344 = 0
ecuación a resolver f (P ) = P 1 +
P
cos π2 1,12
df
arg
0, 931 π
P
derivada de la función
1+
=1+
tan (arg)
arg =
dP
cos (arg)
2
2 1, 12
formula de recurrencia Pn+1 = Pn −
f (Pn )
f ′ (Pn )
lo cual conduce a (empezando con P = 0, 4)
P
P
P
P
= 0, 400
= 0, 502
= 0, 473
= 0, 482
f (P ) = −0, 3137
f (P ) = 0, 1005
f (P ) = −0, 030
f (P ) = 0, 009
f ′ (P ) = 3, 072
f ′ (P ) = 3, 411
f ′ (P ) = 3, 304
Pmáx ≃ 0, 48MN ≃ 48, 9 tn
P
0, 48
P∗ =
= 0, 428
=
PC
1, 12
Es decir que para una excentricidad e = 5 cm = 0, 72 rx = 0, 93 WAx la tensión límite de
propocionalidad se alcanza con una carga del 43 % de la carga crítica.
Simplificación en el cálculo de I para una sección rectangular hueca
Sea una sección rectangular cuyas dimensiones son h y b medidas desde la línea media y de
espesor t. Los momentos de inercia son:
1 (b + t) (h + t)3 − (b − t) (h − t)3
12
1 Iy =
(b + t)3 (h + t) − (b − t)3 (h − t)
12
Ix =
Desarrollando resulta
1 (b + t) h3 + 3h2 t + 3ht2 + t3 − (b − t) h3 − 3h2 t + 3ht2 − t3
12
1 2
=
2b 3h t + t3 + 2t h3 + 3ht2
12
=
Agrupando en potencias de t
6
Ix =
similarmente
1 2
t 6bh + 2h3 + t3 (2b + 6h)
12
1 2
t 6b h + 2b3 + t3 (2h + 6b)
12
Si despreciamos los términos en t3
2
bh
h3
Ix = t
+
2
6
2
b h b3
Iy = t
+
2
6
Iy =
Por ejemplo para h = 30cm, b = 15cm y t = 1cm, los valores exactos y aproximados son:
Imáx
Imı́n
Exacto Aproximado relacion
11267
11250
0, 998
3950
3937
0, 997
7
Mecánica de las Estructuras I
Ejercicios a resolver sobre Pandeo:
Ejercicio 1:
Una columna de 4 m de altura debe resistir una carga máxima Pmax =
60 tn. La columna (orientada en la dirección vertical z) está empotrada-libre
en el plano x − z y articulada-articulada en el plano y − z. Las propiedades
mecánicas del material a utilizar son E = 2 × 106 M P a y σprop = 200 M P a.
Se pide dimensionar la sección con:
a- un perfil normal doble T de alas anchas.
b- una sección rectangular hueca de espesor t = 4 mm y una relación
ancho-altura hb = 0, 35
Ejercicio 2:
Una columna de longitud L = 3, 5 m está articulada-articulada y tiene
una sección PNI16 con propiedades:
A = 54, 3 cm2 , Ix = 2490 cm4 , Iy = 889 cm4 , Wx = 311 cm3 , Wy =
111 cm3 . Se pide
a- bajo una carga P = 30 tn , determinar la máxima excentricidad a
flexión alrededor del eje y.
b- si la excentricidad es ex = 10cm, determinar la carga axial necesaria
para que el material entre en fluencia.
1