¿Quién teme a la energía oscura? “Soy un físico, y por eso mismo

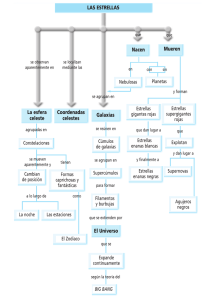
¿Quién teme a la energía oscura?
“Soy un físico, y por eso mismo soy un filósofo e incluso un metafísico. Juicio perfectamente aplicable
los cosmólogos especulativos modernos.”
Octavio Paz, La llama doble
El 10 de diciembre de 2011 se llevó a cabo la ceremonia de los Premio Nobel de Física 2011, los cuales
fueron otorgados a los físicos Saul Perlmutter, Brian Schmidt y Adam Riess, “for the discovery of the
accelerating expansion of the Universe through observations of distant supernovae”. La Academia
Sueca de Ciencias reconoció de esta manera a uno de los descubrimientos científicos más intrigantes de
la Cosmología moderna y que tiene que ver con que las galaxias se alejan unas de las otras con
velocidad creciente con el paso del tiempo. El descubrimiento fue dado a conocer entre 1998 y 1999
por los equipos liderados por los antes mencionados Premios Nobel1.
Además de intrigante, el descubrimiento de la expansión acelerada del Universo es desconcertante
sobre todo debido a que la fuerza de gravedad es la única que debe existir entre cualquier par de
galaxias y todos sabemos que la gravedad es una fuerza atractiva. ¿No debieran entonces las galaxias
atraerse y por tanto alejarse con velocidad decreciente? Y sin embargo la respuesta es la siguiente: la
gravedad no es solo atractiva, sino que también puede ser repulsiva. Lo desconcertante, y al mismo
tiempo sorprendente para nuestra afortunada generación, del descubrimiento de 1998-1999, es que
hayamos encontrado un ejemplo de gravedad repulsiva y de que su manifestación más clara ocurra
precisamente en las escalas cósmicas.
En los párrafos siguientes, haré una descripción sobre las ideas físicas y conceptos matemáticos que
dan sustento a nuestra suposición de que una componente material exótica existe, de que es la
componente material más abundante en el Universo actual y la responsable de que la expansión
cósmica sea cada vez más rápida. Aunque la Física encuentra su expresión más exacta precisamente en
el uso de símbolos y relaciones matemáticas, el uso de las matemáticas será mantenido en su mínima
expresión, pero haré mi mayor esfuerzo para lograr que el texto no deforme en demasía lo que las
ecuaciones de la Física muestran.
El campo gravitatorio del Universo. Para mejor comprender cómo se inserta la expansión acelerada
del Universo en nuestra concepción actual del Unvierso, es indispensable que hablemos de los
conceptos matemáticos y físicos que la rodean. Comencemos haciendo una breve descripción de la
Teoría de la Relatividad General (la cual abreviaremos como TRG), nuestra teoría moderna de la
gravitación, la cual fue formulada en 1915 por Albert Einstein. La TRG establece que la fuerza de
gravedad no es más que la manifestación de la curvatura del espaciotiempo provocada por toda masa
presente. En ese sentido, la gravedad no es una fuerza en el sentido Newtoniano de la palabra (donde
las fuerzas están relacionadas con tensiones, estiramientos, etc.), sino que ahora debemos concebir
(imaginarnos) al espacio y al tiempo como las 4 coordenadas de una superficie curvada en y sobre la
cual los objetos realizan sus movimientos. Esto tiene una consecuencia muy profunda: la fuerza de
gravedad es una manifestación geométrica de las propiedades de una superficie curva (el
1Información
completa puede encontrarse en la página web: http://www.nobelprize.org/nobel_prizes/physics/laureates/2011/
1
espaciotiempo), y como tal su descripción física puede y debe ser dada en términos de conceptos
puramente geométricos.
En 1917, Albert Einstein publica el primer artículo cosmológico en el sentido moderno del término,
“Kosmologische Betrachtungen zur allgemeinen Relativitätstheorie” (Consideraciones cosmológicas
de la Teoría General de la Relatividad) [Preussische Akademie der Wissenschaften (Berlin).
Sitzungsberichte , 142–152]. Ya en ese artículo encontramos un concepto muy importante que ha
delineado fuertemente nuestra idea de Universo (y por el cual parece ser que el mismo Einstein fue
ampliamente criticado por sus contemporáneos): el Principio Cosmológico (de Einstein, y que
abreviaremos como PC), el cual establece que el Universo es espacialmente homogéneo e isotrópico.
Es decir, la composición y propiedades del Universo son las mismas vistas (medidas o cuantificadas)
desde cualquier posición (homogeneidad) y las mismas vistas en cualquier dirección (isotropía). En el
fondo, el PC no es más que la reivindicación del Principio Copernicano que establecía que la Tierra no
ocupaba ninguna posición privilegiada en el Sistema Solar (el Universo según se entendía entonces),
solo que ahora extendido al conjunto de la miles de millones de galaxias que observamos. La utilidad
del PC radica en el hecho de que nos permite acotar la posible geometría del espaciotiempo del
Universo. A través de un ejercicio matemático firmemente establecido, los cálculos culminan en la
escritura de la métrica del Universo que conocemos como la métrica de Friedmann-Roberton-WalkerLemaitre (y que por razones de espacio abreviaremos como FRWL)(Weinberg 1972)(Charles Misner
1973).
En sentido estricto, la métrica de FRWL establece que las propiedades geométricas del espaciotiempo
son isotrópicas alrededor de cualquier punto en el mismo y solo van a tener una dependencia funcional
del tiempo (cambian con el tiempo), que su curvatura espacial es nula2 y que existe una coordenada
temporal particular a la que denotaremos como tiempo cósmico t. De hecho, la única función que lleva
información acerca de los cambios en la métrica es el llamado factor de escala del Unvierso,
usualmente denotado por a(t). Que una sola función del tiempo sea la responsable de llevar a cuestas la
información física del espaciotiempo del Universo no es sorprendente ya que es consecuencia
ineludible de aceptar la validez del PC.
Tan sencillo como pueda parecer, el factor de escala encierra información muy importante sobre cómo
se expande el Universo, la cual está contenida en su valor y en el de sus derivadas temporales, como se
enlista a continuación.
1.Tamaño del Universo. Utilizando la métrica de FRWL, es posible determinar que el factor de escala
actúa como factor de proporcionalidad para la distancia entre nosotros y cualquier otro objeto en el
Universo, digamos otra galaxia. Entonces, decimos que el Universo está en expansión si el factor de
escala es una función creciente del tiempo; por el contrario, el Universo estaría en contracción si el
factor de escala es una función decreciente del tiempo.
2.El parámetro de Hubble H(t). La razón de cambio del factor escala con el tiempo, lo que formalmente
se conoce como su primera derivada temporal, nos da una medida de la velocidad de expansión del
2
El PC permite que en la métrica de FRWL aparezca una curvatura espacial no-nula, pero tomaré un atajo en mi descripción
considerando que tal curvatura es nula, como lo señalan las mismas observaciones cosmológicas. También debe apreciarse
que lo que es nulo es la curvatura espacial, mas sin embargo lo que sigue existiendo es la curvatura del espaciotiempo y por
tanto el Universo está sujeto a un campo gravitacional, tal y como lo demanda la TRG.
2
Universo. Debido a su importancia, esta primera derivada temporal recibe el nombre de parámetro de
Hubble, debido a que fue Edwin Hubble, en 1929, quien primero logró determinar su valor a partir de
las mediciones sobre las velocidades de recesión de galaxias cercanas, véase la Fig. 1. El parámetro de
Hubble es una función cambiante en el tiempo, pero su valor presente nos da una medida de la edad y
tamaño del Universo observable. De acuerdo a mediciones recientes, el valor actual del parámetro de
Hubble es de 72 metro segundo/Megaparsec (estas son las unidades que se manejan por ser las
apropiadas para las escalas cosmológicas), de lo cual inferimos que la edad del Universo es
aproximadamente de 13,700 millones de años, con un tamaño (radio observable alrededor nuestro) de
al menos 13,700 millones de años-luz (no debe olvidarse que un año-luz es la distancia que recorre la
luz en un año, y que corresponde a 9.5 billones de kilómetros.).
3.Parámetro de desaceleración q(t). Este parámetro tiene que ver con la segunda derivada temporal del
factor de escala y mide la razón de cambio de la velocidad de expansión del Universo, es decir, mide la
aceleración de la expansión. Se le ha conocido históricamente como parámetro de desaceleración
porque por mucho tiempo se creyó que el Universo se expandía desaceleradamente.
4.Señales luminosas. Las grandes mensajeras cósmicas son las ondas electromagnéticas, entre las
cuales encontramos las señales que puede captar el ojo humano, que se encuentran en lo que se llama el
espectro visible, o que más en corto conocemos como la luz. Al viajar por el Universo, las ondas
electromagnéticas sienten el efecto de la gravedad a través de lo que se conoce como corrimiento
gravitacional al rojo, que se denota en inglés como redshift y que se representa con la letra z. La
explicación física es que las ondas electromagnéticas pierden energía al viajar en un campo
gravitacional, y por tanto el corrimiento gravitacional al rojo es una medida del cambio temporal del
factor de escala del Universo, es decir, de su expansión. El corrimiento al rojo es la medida usual de
tiempos y distancias en cosmología, y en la tabla siguiente hago un resumen de lo valores usuales del
corrimiento al rojo y su equivalencia con distancias y edades del Universo.
Corrimiento al rojo z
Edad del Universo
(millones de años)
Distancia
(millones de años-luz)
0.0
13,700
0.0
0.1
12,420
1,500
0.5
8,650
9,300
1.0
5,930
22,000
1.5
4,340
36,000
Infinito
0.0
40,000
Tabla 1. El corrimiento al rojo y su relación con la edad del Universo y la distancia cosmológica
respecto de la Tierra que le corresponde. Los valores calculados de los dos últimos fueron determinados
de acuerdo con el Modelo Cosmológico Estándar. De acuerdo a la tabla, el tamaño del Universo
observable es de 40,000 millones de años-luz.
3
Distancias luminosas cosmológicas y supernovas tipo Ia. Para determinar el corrimiento al rojo de
una fuente de luz lejana, que usualmente son las estrellas, basta con conocer su luminosidad intrínseca,
aquella que mediríamos de estar cerca de ella. Esto es realmente imposible para estrellas ubicadas fuera
del Sistema Solar, no digamos para estrellas ubicadas en otras galaxias. Pero el PC viene a nuestro
rescate: las estrellas en cualquier parte del Universo deben tener una composición material igual a la de
las estrellas cercanas a nosotros, en particular, su composición debe ser igual que la de la estrella más
cercana a nosotros: el Sol. Muchas propiedades del Sol las conocemos tanto a través del avance en los
detectores astronómicos como de los avances de la Física de las partículas elementales en los últimos
100 años. Por ejemplo, analizando los espectros de luz del Sol, es decir, analizando en detalle el tipo e
intensidad de radiación electromagnética que emite, es que estamos bastante seguros de que el Sol está
hecho principalmente de Hidrógeno (H) y Helio (He). De acuerdo al entendimiento que tenemos de la
Fisica de partículas elementales, también sabemos que hay una relación entre la masa de una estrella y
el tipo de radiación electromagnética que emite preponderantemente. Estrellas con con poca masa son
de un color rojizo, mientras que estrellas más masivas se ven azuladas. Otra forma de decirlo, es que
las estrellas menos masivas son más calientes que las más masivas. Por tanto, cuando comparamos el
brillo aparente de una estrella con el que hipotéticamente tendría al estar cerca de la Tierra, podemos
calcular la distancia a la que se encuentra. Aquí quiero recalcar la palabra calcular, ya que una
medición física de la distancia es todavia imposible de realizar.
Pero aún una estrella muy masiva es imposible de ver en las grandes distancias cosmológicas a las que
se encuentran de nosotros otras galaxias. Afortunadamente, para eso contamos con la presencia en una
galaxia típica de miles de millones de estrellas, y entonces una galaxia individual puede ser vista a
grandes distancias gracias a la potencia luminosa combinada de todas sus estrellas. De esta manera,
cada galaxia puede ser tratada como un solo objeto luminoso al cual se le puede calcular su corriento al
rojo al analizar su especto luminoso. Desafortunadamente, a diferencia de lo que pasa con estrellas
individuales, no podemos decir cuál es la luminosidad intrínseca de una galaxia, por lo que nos es
imposible calcular sus distancias con sólo medir su brillantez. Para galaxias suficientemente cercanas a
la nuestra, la Vía Láctea, se pueden utilizar diferente métodos geométricos para calcular sus distancias.
Ese fue el trabajo cuidadoso realizado por Edwin Hubble en 1929 y que le dió un lugar de honor en la
historia de la Cosmología; la figura original del descubrimiento del Universo puede apreciarse en la
Figura 1.
4
Figura 1. Diagrama original utilizado por Edwin Hubble en 1929 con el cual mostró evidencia sobre la
expansión del Universo. El eje horizontal mide las distancias en parsecs (1 parsec = 3.26 años-luz),
mientras que el eje vertical muestra los corrimientos al rojo en términos de velocidades, algo común en
esos días, de galaxias cercanas a nuestra Vía Láctea. Este tipo de gráficas recibe desde entonces el
nombre de “diagramas de Hubble”. Puede observarse que las galaxias más lejanas se mueven más
rápido, lo cual se conoce precisamente como Ley de Hubble. La gráfica demuestra la expansión de
Universo, de tal forma que el parámetro de Hubble H(t) es una función positiva, pero no puede dar
ninguna información sobre el parámetro de desaceleración q(t). El máximo corrimiento al rojo
registrado en esta gráfica de Hubble es de z=0.003, que corresponde a una distancia de casi 42 millones
de años-luz de distancia. La figura fue tomada de (Hubble 1929).
Al rescate llegaron las supernovas tipo Ia. Las supernovas denotan, de manera general , las explosiones
violentas de estrellas que han agotado alguno de sus ciclos de vida. Usualmente, las estrellas agotan
alguna fase de su combustible nuclear y la presión de la radiación que producen disminuye, lo que
provoca que la autogravedad de la estrella la haga contraerse y después explotar. En un tiempo del
orden de varios días, la luminosidad de la estrella aumenta para luego disminuir una vez que ha
terminado el ciclo de la explosión. De hecho, la denominación de nova y supernova viene del hecho de
que, en el pasado, estrellas lejanas se hacían visibles al ojo humano al momento de explotar, por lo que
por unos días parecía que en el cielo había aparecido una nueva (nova) estrella donde antes no la había.
Debido al alto número de estrellas en el Universo (miles de millones de estrellas en una galaxia típica,
miles de millones de galaxias típicas distribuidas en todos lados en el Universo) es muy probable que
cada segundo estén ocurriendo explosiones estelares en alguna parte del cielo. Sin embargo, muchas de
ellas no son lo suficientemente intensas como para ser detectadas por nuestros telescopios; pero algunas
de ellas lo son, en particular unas que son denominadas supernovas tipo Ia.
5
Las supernovas tipo Ia son explosiones de estrellas extremadamente poderosas, y por tanto,
extremadamente luminosas; mientras duran, pueden ser tan intensamente brillantes como para superar
la de la galaxia que las aloja. Existe el consenso de que las explosiones corresponden a estrellas enanas
blancas en sistemas binarios, aunque no se ha podido determinar aún el tipo de estrella que las
acompañan (Peter Nugent 2011; Weidong Li 2011). Las supernovas tipo Ia también poseen la
peculiaridad de tener una evolución muy regular (en términos técnicos, una curva de luminosidad muy
regular) que es practicamente la misma independientemente de dónde se encuentren, ver la Figura 2.
Bastó entonces con estudiar las supernovas tipo Ia ocurridas en galaxias cercanas, de las cuales se
podía conocer su distancia utilizando algunos otros métodos astronómicos, para establecer una
calibración que relacionara su luminosidad y la distancia a la que se encuentran. En otras palabras,
sabiendo su luminosidad puede determinarse su distancia, y viceversa. Por supuesto, esto que cuento en
unos cuantas líneas resume el esfuerzo continuo de medir y de entender a las supernovas llevado a cabo
por diversos grupos astronómicos durante varias décadas hasta culminar en los artículos decisivos de
Perlmutter, Schmidt y Riess en 1998-19993 y en el descubrimiento de la expansión acelerada del
Universo, ver por ejemplo la Figura 3.
normalized flux
R
0.4
normalized flux
normalized flux
et. al. (2003)
F814W
0
−40
0
40
80
120
150 550
1997eq
z=0.54
0.4
−40
0
40
80
120
150 550
F675W
0.4
0
−40
0
40
80
120
150 550
1997ez
z=0.78
0.8
0.4
−250
−40
0
40
80
120
150 550
F814W
0.8
0.4
0
0
−40
0
40
80
120
150 550
1998as
z=0.35
0.8
0.4
−250
−40
0
40
80
120
150 550
F675W
0.8
0.4
0
0
−40
0
40
80
120
150 350
1998aw
z=0.44
0.8
0.4
−250
−40
0
40
80
120
150 550
F675W
0.8
0.4
0
−450
−250
0.8
0
−250
band
0.4
0.8
−250
I
0.8
0
−250
normalized flux
1997ek
z=0.86
0.8
−250
normalized flux
Knop
band
0
−40
0
40
80
Observed day from peak
120
150 550
−450
−40
0
40
80
120
150 550
Observed day from peak
Figura 2. Curvas de luminosidad de 5 supernovas tipo Ia (de arriba hacia abajo), en dos bandas
diferentes de observación. Puede observarse que la duración de las explosiones es de aproximadamente
40 días a partir del máximo de la curva (una vez que las curvas han sido calibradas apropiadamente con
supernovas cercanas), y que la forma de las curvas es bastante similar para todos los casos. Figura
tomada de (Robert Knop 2003).
3
Actualmente se cuenta con catálogos de aproximadamente 500 supernovas tipo Ia, con los cuales los estudios de la
expansión del Universo no han hecho más que comprobar su aceleración actual. En el futuro cercano, se espera aumentar el
numero de supernovas hasta más allá del millar con la ayuda de nuevos telescopios espaciales.
6
Figura 3. Moderno diagrama de Hubble realizado con las mediciones de supernovas tipo Ia hasta el año
2003. A diferencia de lo hecho por Hubble (ver la Figura 1), en este diagrama el máximo corrimiento al
rojo detectado es de z=1.0 (escala vertical derecha), que corresponde a una supernova que explotó
cuando el Universo tenía la mitad de su tamaño actual y una tercera parte de su edad presente, es decir,
la supernova ocurrió hace casi 10 mil millones de años. Adicionalmente, podemos observar en la
misma gráfica que las supernovas tipo Ia indican una preferencia por Universos cuya expansión
primero desacelera y después acelera (lineas verdes). La figura fue tomada de (Perlmutter 2003).
La energía oscura. Una vez descubierta la expansión acelerada del Universo, queda aún abierta la
interrogante de cómo es posible lograr una gravedad repulsiva. Para esto, debemos dejar la cinemática
(estudio de la expansión del Universo), y concentrarnos ahora en la dinámica para descubrir a los
agentes responsables. Debemos recurrir a las famosas ecuaciones de Einstein de la TRG; éstas son
ecuaciones tensoriales que forman un conjunto acoplado de 10 ecuaciones independientes en derivadas
parciales no-lineales. De inicio, las ecuaciones de Einstein son un reto matemático enorme si uno
intenta resolverlas de manera general. Afortunadamente para nosotros (y para el Universo), el PC llega
de nuevo a nuestro rescate. Para un universo espacialmente homogéneo e isotrópico, las ecuaciones de
Einstein son solamente un par de ecuaciones acopladas no lineales en derivadas ordinarias; una de ellas
se refiere a la velocidad de expansión del universo, y la otra se refiere a la aceleración de la expansión
del universo. La segunda es la que nos importa principalmente, por lo que nos concentraremos en ella.
7
Pero primero debemos hablar un poco sobre la materia del Universo. Las ecuaciones de Einstein
relacionan la geometría del espaciotiempo con las fuentes del campo gravitatorio, que no son otra cosa
que los campos materiales que nos interesan. Un concepto del que echaremos mano es el de un fluido
cósmico. La palabra fluido nos remite directamente a imágenes sobre el agua y el aire (o cualquier otro
líquido o gas), para los cuales nos interesa conocer solo propiedades medias generales: densidad,
presión, composición, etc., sin ahondar mucho en lo que pasa dentro del mismo punto por punto. Pero
esa es precisamente la imagen que necesitamos para pensar sobre la materia en el Universo: partículas
distribuidas de manera uniforme y homogénea (si así no lo fuera, romperíamos el PC). Por partículas
me puedo referir a fotones (partículas de luz), átomos, etc., o hasta a estrellas o galaxias. Entonces, lo
único que nos interesará conocer es la densidad de energía y la presión medias de cada fluido cósmico
material que compone al Universo.
Si el Universo se rigiera estrictamente por la Ley de la Gravitación Universal de Newton, entonces en
la ecuación de aceleración solo debería aparecer la densidad de energía del fluido cósmico como
provocadora de la fuerza de gravitación. Por el contrario, de acuerdo a la TRG, la presión del fluido
también contribuye en la generación del campo gravitacional. Las ecuaciones de Einstein muestran que
una expansión acelerada del Universo es posible si el fluido cósmico dominante tiene una presión
negativa.
Tan extraño como pueda sonar, la TRG permite la presencia de gravedad repulsiva siempre y cuando la
materia presente cumpla con la condición arriba mencionada. Tal relación no es satisfecha (si es que
usted amable lector se lo está preguntando en estos momentos) por materia alguna de la que conocemos
en nuestro entorno cercano y con la cual tengamos contacto diario. Sin embargo, el Universo parece
sugerirla si es que queremos explicar las observaciones sobre la luminosidad de supernovas tipo Ia
lejanas. Este es el origen de nuestra creencia en la existencia de una componente material, muy exótica,
que es capaz de acelerar la velocidad a la que se alejan las galaxias unas de otras en el Universo, y a la
que denominamos genéricamente como energía oscura (Matos 2004).
La constante cosmológica de Einstein. Han pasado mas de una decena de años en los que la
comunidad de cosmológos teóricos ha trabajado intensamente para descifrar el misterio de la
composición de la energía oscura. Sin embargo, ningun modelo ha sido lo suficientemente satisfactorio
como para dejar a la comunidad con la sensación que hemos resuelto el misterio de la expansión
acelerada. Pero entre todos los modelos, uno destaca por ser extremadamente sencillo, de hecho es el
más sencillo de todos, aunque su naturaleza fundamental sea todavía un enigma. Se trata de la
constante cosmológica (que abreviaremos como CC), una predicción teórica de la TRG que el mismo
Einstein utilizó en sus modelos cosmológicos. Esta CC debe ser considerada como una constante
fundamental de la naturaleza, al mismo nivel que lo son la velocidad de la luz en el vacío, la constante
de Planck, la masa y carga del electrón, entre otras.
Por mucho tiempo la utilidad de la CC se mantuvo en duda, y la mejor suposición que podía hacerse
era considerar que su valor era exactamente cero, aunque pronto se supo que, con un valor aceptable,
sería capaz de provocar una expansión acelerada del Universo. De hecho, es posible mostrar
formalmente que la CC es equivalente a un fluido exótico que cumple exactamente con que su presión
8
es el negativo exacto de su densidad de energía (en las unidades apropiadas), ¡cumpliendo ampliamente
la condición para ser un candidato aceptable de energía oscura!
Las dificultades aparecen cuando los cosmólogos, y los físicos en general, intentamos explicar por qué
la CC debe tener precisamente el valor determinado por las observaciones cosmológicas. No es posible
entender ese valor con ninguna de las ideas o conceptos que conocemos actualmente, por lo que la
comprensión de nuestro propuesta más sencilla para la energía oscura debe esperar a un desarrollo
futuro de las teorías físicas (ver (Banks 2004)).
Figura 4. Restricciones cosmológicas sobre las contribuciones porcentuales de materia (materia oscura
más materia ordinaria como átomos, neutrinos y fotones) y de la CC, de acuerdo al Modelo
Cosmológico Estándar. La CC contribuiría con aproximadamente el 70% del contenido material en el
Universo presente. Las observaciones cosmológicas son las supernovas tipo Ia (SNe), la radiación del
fondo cósmico (CMB, por las siglas en inglés de Cosmic Microwave Background), y de las
oscilaciones acústicas bariónicas (BAO, por las siglas en inglés de Baryonic Acoustic Oscillations).
Figura tomada de (R. Amanullah 2010).
Mientras tanto, nuestro mejor modelo cosmológico considera precisamente que la energía oscura es una
CC, a falta de un mejor prospecto. En la Figura 4 podemos apreciar las regiones de confianza señaladas
por diversas observaciones cosmológicas y las restricciones que imponen sobre las contribuciones
porcentuales de materia y la CC en el Universo presente. Las regiones de confianza son muy grandes,
como es típico en la Cosmología, pero todas parecen coincidir en una región pequeña del espacio de
parámetros, que indicaría que la CC contribuye con aproximadamente el 70% de la materia total. Con
9
esto se configura lo que se llama el Modelo Estándar Cosmológico (o de la Coincidencia Cósmica, por
la coincidencia de las observaciones cosmológicas en la Figura 4).
Apuntes finales. La búsqueda de modelos más satisfactorios de la energía oscura tiene todavía mucha
vida por delante. Mencionaré brevemente aquellos que han ganado mayor notoriedad. En primer lugar,
están los modelos de gravedad modificada, así llamados porque parten de la hipótesis de que la TRG no
es la versión ultima de la gravedad, sino solo un paso intermedio(Ruth Durrer 2008). Así como el
origen de la CC fue meramente geométrico, se pueden aventurar toda una serie de modificaciones a la
TRG que en principio siguen siendo compatibles con los principios teóricos que le dieron origen. Sin
embargo, las versiones más sencillas (aunque notoriamente más elaboradas que una simple CC) no han
probado ser mejores modelos que la CC. Lo mismo sucede con las teorías multi-dimensionales, en las
que se propone que nuestro Universo contiene más de 3 coordenadas espaciales y la gravedad es un
campo capaz de propagarse en todas ellas, de tal forma que la expansión acelerada no es otra cosa que
el universo multidimensional proyectado sobre el espaciotiempo cuadridimensional accesible a
nuestros sentidos.
Por otro lado tenemos la versión de que el Universo es realmente infinito en extensión, y que las
propiedades físicas que observamos cambian de una región a otra del mismo (Max Tegmark 2006). La
región en la que existimos comenzó a expandirse hace 13,700 millones de años y coincidentemente
tiene los valores físicos adecuados para finalmente producir la vida como la conocemos. En esta región
del universo, la CC tiene el valor adecuado para acelerar la expansión cósmica; en otras regiones, la CC
tomaría otros valores, para los cuales probablemente no hay expansión acelerada, y el universo luce
muy diferente al de nuestra región observable. Este tipo de razonamiento está influido por el llamado
Principio Antrópico, que establece que las condiciones físicas del Universo son las adecuadas para
producir seres humanos como nosotros, de tal forma que nuestra existencia se convierte en el método
de selección de los parámetros físicos del Universo (solo son permitidos aquellos valores que
permitieron en algún punto la aparición de la vida sobre la Tierra). Desafortunadamente, este tipo de
razonamientos no han sido muy convincentes, ya que no se ha mostrado hasta la fecha una prueba de
que nuestra existencia sea altamente probable entre las opciones presentadas por un universo infinito.
El misterio de la energía oscura es probablemente el acertijo cosmológico que más retos presentará a
las generaciones de físicos del siglo XXI. Para cualquier otro, existen esperanzas fundadas de encontrar
su explicación partiendo de nuestras ideas físicas actuales, como es el caso, por ejemplo, de la materia
oscura, para la cual se han diseñado cualquier número de aparatos detectores terrestres y se tiene la
esperanza de también cazarla en los grandes aceleradores de partículas. Pero la energía oscura es un
ente diferente, que de forma casi inevitable nos obliga a mirar en las grandes escalas cósmicas para su
detección, con nulas expectativas de detectarlo en las escalas galácticas, no digamos en las escalas del
Sistema Solar y mucho menos en las de los laboratorios terrestres. Por esa misma dificultad, todos
estamos seguros de que con cada pedazo de información que logremos arrancarle, estaremos teniendo
acceso a un cosmos completamente nuevo, literalmente hablando.
No me resta más que cerrar este artículo tomando prestadas unas palabras escritas con buen tino y
mejor prosa por el Premio Nobel de Literatura Octavio Paz, en su libro La llama doble: “O sea, el
cosmos tiene una historia y uno de los objetivos de la ciencia es conocer esa historia y contarla. La
física se volvió crónica del cosmos. ... las preguntas que hoy se hacen los científicos se las hicieron,
10
hace dos mil quinientos años, los filósofos jónicos, fundadores del pensamiento occidental ... estas
preguntas hoy regresan y son tan actuales como en los albores de nuestra civilización.”(Paz 1993)
Bibliography
Banks, T. (2004). "The Cosmological Constant Problem." Physics Today 57(3).
Charles Misner, a. K. T., and John Wheeler (1973). Gravitation, Freeman.
Hubble, E. (1929). "A relation between distance and radial velocity among extra-galactic nebulae."
Proceedings of the National Academy of Sciences of the United States of America 29.
Matos, T. (2004). ¿De qué está hecho el Universo?, Fondo de Cultura Económica.
Max Tegmark, A. A., and Martin Rees (2006). "Dimensionless constants, cosmology and other dark
matters." Physical Review D 73(023505).
Paz, O. (1993). La llama doble, Seix Barral.
Perlmutter, S. (2003). "Supernovae, dark energy, and the accelerating universe." Physics Today 56(4):
6.
Peter Nugent, e. a. (2011). "Supernova SN 2011fe from an exploding carbon-oxygen white dwarf star."
Nature 480.
R. Amanullah, e. a. (2010). "Spectra and Light Curves of Six Type Ia Supernovae at 0.511 < z < 1.12
and the Union2 Compilation." Astrophysical Journal 716: 16.
Robert Knop, e. a. (2003). "New constraints on OmegaM, OmegaLambda, and w from an independent
set of eleven high-redshift supernovae observed with HST." Astrophysical Journal 598: 10.
Ruth Durrer, a. R. M. (2008). "Dark energy and modified gravity." arXiv:0811.4132.
Weidong Li, e. a. (2011). "Exclusion of a luminous red giant as a companion star to the progenitor of
supernova 2011fe." Nature 480.
Weinberg, S. (1972). Gravitation and Cosmology, Wiley.
11