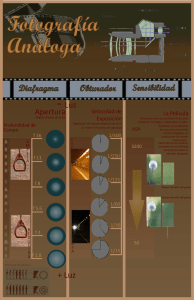
Tema6.MaterialesCERAMICOS.SinterizacionEstadoSolido

TEMA 13 .- Sinterización en estado sólido (SSS).
0.- Introducción.
Casi todos los cuerpos cerámicos deben ser sinterizados para producir una microestructura con las
propiedades requeridas. En la práctica, el ceramista, desea preparar un material con un conjunto particular
de propiedades, por lo que identifica la microestructura requerida y trata de diseñar las condiciones de
tratamiento que producirán dicha microestructura. El objetivo clave de los estudios de sinterización es, por
lo tanto, entender como las variables del proceso influyen en la evolución microestructural. De este modo,
información útil puede derivarse del esfuerzo práctico de diseñar condiciones de proceso para producir la
microestructura requerida.
Una aproximación al desarrollo de un entendimiento del proceso de sinterización es conectar el
comportamiento o cambios en el comportamiento durante la sinterización a variables y procesos
controlables. Esto puede alcanzarse empíricamente midiendo el comportamiento de sinterización bajo un
conjunto de condiciones controladas o teóricamente modelizando el proceso. Los análisis teóricos y estudios
experimentales realizados durante los últimos 50 años pasados han producido un excelente entendimiento
cualitativo de la sinterización en términos de las fuerzas motrices, los mecanismos y la influencia de las
principales variables del proceso como son: el tamaño de partícula, la temperatura y la presión aplicada. Sin
embargo, la base de datos y los modelos son mucho menos acertados en el suministro de una descripción
cuantitativa de la sinterización para la mayor parte de los sistemas de interés.
La tabla 0.1 listas algunos parámetros importantes en la sinterización que puede servir para ilustrar el
alcance del problema.
Tabla 10.1.- Algunos parámetros importantes en el proceso de sinterización de cerámicas.
En general, el procesado y los parámetros de los materiales proporcionan un conjunto útil de variables para
los modelos experimentales y los estudios teóricos. Algunos parámetros, tales como la temperatura de
sinterización, la presión aplicada, el tamaño medio de partícula y la atmósfera gaseosa, pueden ser controlados
con la exactitud suficiente. Otros parámetros, como las características del polvo y el empaquetamiento de las
partículas, son más difíciles de controlar, pero tienen un efecto significativo sobre la sinterización.
Existe una falta de información para parámetros fundamentales como son las energía de superficie y de
límite de grano y los coeficientes de difusión. Esta carencia de información unida a la complejidad de los
sistemas prácticos cerámicos hace que las predicciones cuantitativas del comportamiento durante la
sinterización sean muy difíciles hasta para los sistemas más simples.
Para que la sinterización ocurra, debe haber una disminución en la energía libre del sistema. La curvatura de
las superficies libres y la presión aplicada, cuando sea usada, proporciona la motivación principal o la fuerza
motriz para que la sinterización tenga lugar. Sin embargo, para lograr el proceso dentro de un tiempo
razonable, también se debe considerar la cinética del transporte de materia. En las cerámicas cristalinas, el
transporte de materia ocurre, predominantemente, por la difusión de átomos, iones u otras especies cargadas.
La difusión en estado sólido puede ocurrir por varios caminos que definen los mecanismos de difusión y, de
ahí, los mecanismos de sinterización.
La velocidad de difusión depende del tipo y concentración de defectos en el sólido, entonces un entendimiento
de la estructura de los defectos y los cambios de su concentración (Química de los defectos) es importante.
También se debe entender como la química de los defectos se puede controlar por variables claves en el
proceso de sinterización como son: la temperatura, la atmósfera gaseosa del horno y los solutos (dopantes).
Para predecir como depende la velocidad de sinterización de las variables de procesado primarias, deben
formularse ecuaciones para el flujo de materia, que deben solucionarse sujetas a las condiciones límites o de
frontera apropiadas. El transporte de materia puede verse en términos de flujo de átomos (iones) o,
equivalentemente, en términos del contraflujo de vacantes.
Siguiendo las leyes de Fick de la difusión,


Especies que difunden
dC
= −D
Jx 

dx
 (Unidad área )(Unidad tiempo) 
dC
d 2C
=D 2
dt
dx
(Pr imera ley de Fick )
( Segunda ley de Fick )
(0.1)
(0.2)
el flujo puede analizarse en términos del gradiente de concentración de la especie que se difunde, pero las
ecuaciones toman una forma más generalizada cuando se expresan en términos del potencial químico (
energía libre molar de Gibbs). En este caso, el transporte de materia ocurre de las regiones de potencial
químico más alto a las regiones de potencial químico inferior. En los sólidos inorgánicos, los diferentes iones
o especies cargadas difunden a velocidades diferentes pero el transporte de materia debe ocurrir de tal modo
que la estequiometría y electroneutralidad de los sólidos se conserve. Por lo tanto, la difusión de los iones esta
acoplada y esta difusión acoplada se denomina como la difusión ambipolar.
2
Los fenómenos de sinterización en materiales policristalinos son bastante más complejos que aquellos que
tienen lugar en la sinterización viscosa de materiales amorfos debido a la disponibilidad de varios caminos de
transporte de materia y la presencia de fronteras o límites de grano. El transporte de materia en la
sinterización en estado sólido puede ocurrir por al menos seis caminos diferentes que definen los mecanismos
de sinterización. En la práctica, más de un mecanismo puede funcionar durante cualquier régimen dado de
sinterización y la presencia de múltiples mecanismos hace que se complicado el análisis de la velocidad de
sinterización y la determinación de los mecanismos de sinterización.
Quizás la consecuencia más importante de la presencia de las fronteras de grano es que tenga lugar el
crecimiento de grano durante la sinterización, un proceso normalmente denominado en ingles como
“coarsening”. Este proceso de aumento del tamaño de grano proporciona una ruta alternativa por la cual se
puede reducir la energía libre del sistema en polvo, por lo tanto, esto reduce la fuerza motriz para
densificación.
En contraste con la sinterización en estado sólido, el análisis de la sinterización viscosa parece, en principio,
relativamente simple. El transporte de materia ocurre por un mecanismo de flujo viscoso, pero el camino a lo
largo del cual tiene lugar el flujo de materia no se especifica. En cambio las ecuaciones para el transporte de
materia se deducen tomando como base un concepto de balance de energía propuesto por Frenkel, en el cual
la velocidad de disipación de energía por el flujo viscoso es igual a la velocidad de energía ganada por la
reducción del área de la superficie. Los modelos basados en este concepto de balance de energía son ,
generalmente, acertados en la descripción de la cinética de sinterización de materiales amorfos.
Una teoría comprensiva de la sinterización debería ser capaz de describir enteramente el proceso de
sinterización, así como la evolución de la microestructura (por ejemplo, el tamaño de grano y de poro y la
distribución tamaños de grano y de poro). Sin embargo, en vista de la naturaleza compleja del proceso, es
improbable que tal teoría pueda ser desarrollada. Una aproximación más realista, que se puede adoptar, es
desarrollar primero de forma separada un entendimiento de los fenómenos de la densificación y del aumento
del tamaño de grano y luego explorar las consecuencias de su interacción.
Se han usado varias aproximaciones teóricas para analizar el proceso de densificación durante la
sinterización, incluyendo el empleo de modelos analíticos, leyes de escala y simulaciones numéricas. Estas
aproximaciones, en particular los modelos analíticos, han sido criticados porque las simplificaciones drásticas
que se asumen en los modelos los hacen inadecuados para predecir cuantitativamente el comportamiento
durante la sinterización de los sistemas en polvo reales.
Comúnmente, los modelos asumen un empaquetamiento uniforme de partículas esféricas del mismo tamaño,
la presencia de un solo mecanismo para el transporte de materia y ningún crecimiento de grano. A lo más, los
modelos proporcionan un entendimiento cualitativo de la sinterización. A pesar de esos defectos, el papel de
los modelos teóricos en el desarrollo del entendimiento de sinterización no debería ser pasado por alto.
Otras aproximaciones, como las ecuaciones fenomenológicas y mapas de sinterización, intentan representar
los datos de la sinterización en términos de ecuaciones o diagramas, pero proporcionar muy poca idea en el
proceso.
3
1.-Definición.
Debido a su alto punto de fusión, dureza y fragilidad, los componentes cerámicos no pueden ser fabricados
por los procesos que se usan para los metales y polímeros. En la figura 1.1 puede verse un esquema
simplificado de la fabricación de los materiales cerámicos, del cual forma parte la sinterización.
Figura 1.1.- Esquema general del proceso de fabricación de materiales cerámicos.
La sinterización es el proceso de tratamiento térmico (Cocción), con o sin aplicación de presión externa, de un
sistema de partículas individuales (metálicas, cerámicas, poliméricas) en forma de un aglomerado poroso
4
compacto (previamente conformado), con el objeto de transformarlo en un producto denso que evoluciona
hacia un estado de máxima compactación (Reducción de la porosidad, tendiendo a que sea nula) y
resistente, como resultado de la unión entre las partículas adyacentes del material, sin que se llegue a la
fusión total.
La unión de las partículas se produce a una temperatura suficiente (T < TF) con el fin de estimular los
mecanismos de transporte de masa.
La sinterización puede ocurrir con la presencia o ausencia de una fase líquida. En el primer caso, se denomina
sinterización en presencia de fase líquida, donde las composiciones y temperaturas de calentamiento son
elegidas de tal forma que se origine un líquido durante el procesamiento. En ausencia de una fase líquida, el
proceso se denomina sinterización en estado sólido.
Tal definición del proceso de sinterización engloba los siguientes hechos o fenómenos, de forma explicita o
implícita:
(a).- Necesidad de energía térmica (temperatura) para que el sistema evolucione (activación térmica).
(b).- Se produce un aumento de la cohesión por formación de puentes o cuellos entre las partículas, que llegan a
"soldarse" en estado sólido unas a otras (solid-state sintering o diffusion bonding), como puede apreciarse en la
figura 1.2.
Figura 1.2.- Formación de cuellos debido a la sinterización.
(c).- Se opera un proceso de densificación que elimina progresivamente la porosidad inicial.
(d).- Las partículas individuales que integran, inicialmente el sistema, pueden ser de la misma ó diferente
naturaleza.
(e).- La sinterización, para llevarse a cabo, no necesita del concurso de una presión externa aplicada, pero,
eventualmente, con objeto de acelerar el proceso, pudiera hacerse use de ella (pressure sintering).
(f).- Aunque el vocablo sinterización implica que, al menos, exista una fase sólida, durante el tratamiento
térmico, es posible (y muchas veces deseable ó necesario) la presencia de una fase liquida, de modo
transitorio (liquido reactivo) ó permanente (liquido de equilibrio) durante el proceso.
(g).- Al final de la sinterización, el sistema no tiene porque haber alcanzado el estado de energía libre
mínima pero, indefectiblemente, se encuentra mas cerca de el que al principio.
Los cambios que tienen lugar durante el proceso de sinterización son:
(1).- Reducción de la energía interna del sistema de partículas inicial. Este tiende hacia un estado de equilibrio
que le confiere una estabilidad de forma y dimensiones.
(2).- Disminución de un modo importante de la porosidad inicial (cambios en la forma, tamaño y distribución de
los poros) (Figura 1.3).
5
(3).- Crecimiento de grano (cristal), con posibles recristalizaciones (cambios en el tamaño y la forma de los
granos (cristales)).
(4).- Cristalización o vitrificación parcial.
(5).- Difusión en estado sólido, líquido o gaseoso.
(6).- Cambios de fase.
(7).- Variación de las propiedades físicas (resistencia mecánica, conductividad térmica, traslucencia, etc)
Figura 1.3.- Cambios en la forma y tamaño de los poros durante el proceso de sinterización
En la cocción de los productos cerámicos, paralelamente a las reacciones quimico-fisicas que en ella se
desarrollan, que dan lugar a la formación de nuevas fases cristalinas y vítreas, tiene lugar una serie de
cambios microestructurales de la pieza. El cambio en la forma y tamaño de los poros es uno de los más
importantes, ya que gran parte de las propiedades físicas del producto cocido son dependientes de este
parámetro (resistencia mecánica, resistencia al choque térmico, resistencia a las heladas, expansión por
humedad, etc.).
Para aumentar el valor de algunas de las propiedades, es deseable eliminar tanta porosidad como sea posible,
lo que se consigue durante el tratamiento térmico, mediante la transferencia de materia de unas partes a otras
del compacto poroso y mediante la disminución de volumen.
2.- Etapas de la sinterización.
6
Cuando dos o más partículas sólidas de un material capaz de sinterizarse se ponen en contacto y son
sometidas a un ciclo de cocción determinado, el comportamiento de estas se puede esquematizar en tres
etapas idealizadas: Inicial o formación de cuellos (Necking stage), intermedia (Densificación y crecimiento
de granos) y final (Formación de porosidad cerrada). En la tabla 2.1 se dan los cambios microestructurales
que se presentan en las etapas inicial, intermedia y final de la sinterización en el estado sólido y en la figura
2.1 puede verse, de forma esquemática, el avance del fenómeno de la sinterización.
Tabla 2.1.- Cambios microestructurales presentes en las diferentes etapas de la sinterización.
(i).- Primera etapa o inicial
- Reordenamiento
- Formación de cuellos o puentes (necking stage) entre partículas y su crecimiento.
- Se presentan enlaces en los contactos entre las partículas. Relación (X/D) < 0.3
- Formación de los límites de grano
- Suavizado de la superficie de las partículas
- Redondeo de los poros abiertos interconectados
- Difusión de dopantes segregados
- Disminución de la porosidad (< 12 %)
(ii).- Segunda etapa o intermedia (Cubre la mayor parte del proceso de sinterización)
- Se produce una contracción de los poros abiertos por intersección con los límites de grano.
- Crecimiento de cuellos
- Crecimiento lento de granos.
- Alta contracción (Densificación). La porosidad decrece significativamente.
- Los poros van siendo esféricos y aislados
- Fase continua de poros.
(iii).- Tercera etapa o final
Final (1)
- La densidad es, aproximadamente, del 92 % de la teórica (> 85 % en materiales heterogéneos)
- Intenso crecimiento de granos.
- Fase discontinua de poros (Formación de porosidad cerrada). Se forma poros aislados e interceptan
los límites de grano
- Se produce una contracción de los poros a un tamaño limitado o incluso desaparecen
- Eliminación de poros en las juntas de grano
- Los poros mayores que los granos contraen relativamente lento
- En general, hay movilidad de poros y borde de grano.
Final (2)
- Aparecen rápidamente granos mucho mayores
- Contracción lenta de los poros que se encuentran en el interior de los granos grandes.
7
Figura 2.1.- Esquema de las etapas en la sinterización.
(a).- Polvo de partida. Esferas tangentes
(b).- Etapa inicial, Cerca del final de esta etapa las esferas comienzan a coalescer
(c).- Etapa intermedia. Los granos adoptan la forma de un tetracaidecaedron, encerrando canales de
poros en los bordes de grano
(d).- Etapa final. Los poros son inclusiones tetraédricas en los vértices donde se encuentran cuatro
tetracaidecaedros.
8
Algunos de los parámetros asociados con las tres etapas idealizadas del proceso de sinterización se
resumen en la tabla 2.2 y en la figura 2.2 se da un ejemplo de microestructura real (Sección plana) de
compactos de polvo en las etapas inicial, intermedia y final.
Figura 2.2.- Ejemplos de microestructuras reales (Secciones planas) para:
(a).- Etapa inicial (b).- Etapa intermedia (c).- Etapa final
9
Tabla 2.2.- Parámetros asociados con las etapas de sinterizacion de sólidos policristalinos.
(i).- Primera etapa. Formación de cuellos (necking stage)
Esta etapa inicial tiene lugar, cuando las partículas comienzan a unirse entre si, mediante la formación de
cuellos (Figura 2.1). En este estado de la sinterización no tiene lugar un crecimiento apreciable de los granos
y la contracción macroscópica de la muestra es prácticamente inapreciable. Es posible, sin embargo, seguir la
sinterización en este estado, mediante la evolución de la superficie específica de la muestra que disminuye
mientras la sinterización avanza.
Figura 2.1.- Formación de cuellos a partir de dos partículas esféricas.
Cambios que ocurren durante la etapa inicial de la sinterización: (a).- Partículas de partida (b).Reordenamiento (c).- Formación de cuellos
Los radios de los cuellos, crecen en el estado inicial variando de cero a ≈ 0.2-0.3 del radio de las partículas.
Además, hay una menor rugosidad de las superficies. Durante este estado la densidad relativa se incrementa
del 60 al 65 %, esto es que hay una reducción lenta de la porosidad.
10
(ii).- Segunda etapa. Densificación y crecimiento de los granos.
Paso a paso con el avance de la sinterización, se observa un crecimiento de los granos de material,
perdiendo estos su identidad. Los cuellos se engrosan creando una estructura tridimensional, en la que las
partículas tienden a redondear los espacios vacíos, formando una textura porosa.
Los poros en este estado tienden a formar una estructura continua y abierta. Con el avance de la
sinterización se puede alcanzar una densidad de material del 80 % a 90 % de la densidad teórica. A partir de
este momento se inicia la formación de poros cerrados, que conduce al estado final de la sinterización.
El efecto macroscópico más característico en esta etapa de la sinterización, es una marcada contracción de
la muestra, que alcanza casi el valor final de todo el proceso. Paralelamente al aumento de la contracción,
tiene lugar una reducción intensa de la porosidad abierta y consecuentemente un aumento de la densidad
aparente del material (Figura 2.2).
Figura 2.2.- Cambios que ocurren durante la segunda etapa de la sinterización:
(a).- Crecimiento de los cuellos y contracción de volumen
(b).- Alargamiento de los bordes de grano
(c).- Continua el crecimiento de los cuellos, el alargamiento de los bordes de grano y la contracción
de volumen y hay un crecimiento de grano.
Este estado intermedio se caracteriza por la presencia de canales de poros continuos, coincidentes con las
confluencias de tres partículas.
11
(iii).- Tercera etapa. Formación de porosidad cerrada.
En esta etapa de la sinterización, los poros tienden a conseguir la forma esférica, perdiendo su textura continua
y se aíslan en la masa de la pieza. La velocidad de sinterización disminuye y el aumento de la contracción de
la pieza es mucho menos marcado que en la etapa anterior, hasta el punto de resultar difícil determinar con
exactitud cuando ha finalizado el proceso de sinterización.
Esta etapa final de la sinterización implica la eliminación de la porosidad final, que desaparece por la difusión
de vacantes a lo largo de las fronteras de grano. Por lo tanto, los poros deben permanecer cerca de las
fronteras de grano.
La eliminación de los poros y la difusión de vacantes se favorece por el movimiento de las fronteras de grano
y el crecimiento controlado de grano. Sin embargo, si el crecimiento de grano es demasiado rápido, las
fronteras de grano pueden moverse más rápido que los poros y , por tanto, dejarlos aislados dentro de un
grano. Como el grano sigue creciendo, el poro cada vez está más lejos del borde de grano y disminuye la
posibilidad de su eliminación. Por lo tanto, el crecimiento de grano debe ser controlado para alcanzar la
máxima eliminaión de porosidad.
Las fronteras curvas de los granos se mueven de tal modo que posean un radio de curvatura más grande, es
decir, se enderezan. Esto sólo puede lograrse por el crecimiento de los granos. Los granos más pequeños
tienen un radio de curvatura más pequeño y, por tanto, más energía motriz para moverse, cambiar de forma,
y hasta ser consumido por los granos más grandes.
Los cambios físicos que ocurren durante la etapa final de la sinterizacion se ilustran en la figura 2.3. La
distribución final de granos y poros se denomina microestructura.
Figura 2.3.- Figura 2.2.- Cambios que ocurren durante la etapa final de la sinterización: (a).- Crecimiento de
los granos y porosidad discontinua (b).- Continúa el crecimiento de grano y se reduce la
porosidad (c).- Continua el crecimiento de grano y se elimina la porosidad
Los canales de poros se rompen, formándose poros aislados. Esto comunmente ocurre cuando la densidad de
la muestra se ha incrementado hasta ≈ 92 % de la densidad teórica del material. Los poros individuales son o
de forma lenticular, si se sitúan sobre los bordes de grano, o redondeados, si se distribuyen dentro de un
grano. Una característica importante de este estado es el aumento en las movilidades de los poros y de los
bordes de grano, que tiene que ser controlado si se quiere alcanzar la densidad teórica.
12
3.- Energías motrices de la sinterización.
3.1.- Introducción.
Para que cualquier sistema, homogéneo o heterogéneo, evolucione (por ejemplo, para que un material pulverulento
y poroso de lugar a un producto sinterizado), deberá existir una energía motriz (driving force) que lo impulse
hacia otro estado de energía mas pequeña (véase mínima) y, por tanto, de máxima estabilidad termodinámica.
Las fuentes que dan lugar a esa disminución de la energía libre se denominan, comúnmente, fuerzas o
energías motrices de la sinterización. Existen tres posibles fuerzas motrices principales (Figura 3.1.1):
1.- Curvatura de la superficie de las partículas.
2.- Presión aplicada externamente.
3.- Reacción química.
Figura 3.1.1.- Diagrama esquemático ilustrando las tres principales fuerzas motrices de la sinterización
(a).- Curvatura de la superficie de las partículas (b).- Presión aplicada externamente.
(c).- Reacción química.
La tendencia teórica, que permite comprender el proceso de sinterización, es aquella que considera como
fuerza motriz del proceso "el exceso de energía libre superficial" presente en un sistema finamente disperso,
sobre el de un sistema sinterizado.
La energía (fuerza) motriz puede variar a lo largo del proceso. Parece lógico pensar que la fuerza impulsora
para la formación de puentes entre las partículas, que opera durante las primeras etapas de la sinterización, será
de diferente naturaleza a la que opera con objeto de eliminar la porosidad residual en el interior de los granos o
partículas ya "soldadas", o a la que hace posible una transformación alotrópica en el calentamiento (por ejemplo, del
cuarzo en tridimita y en cristobalita respectivamente) o una transformación por cizallamiento en un
enfriamiento de no equilibrio (por ejemplo, de la cristobalita - α en cristobalita - β ). De modo que varios tipos
de fuerzas impulsoras pueden intervenir sucesiva o simultáneamente durante el proceso de sinterización.
13
La fuerza conductora global para la sinterización tiene su origen en la reducción de la energía libre total ∆GT
del sistema,
∆GT = ∆GV + ∆GB + ∆GS
(3.1.1)
Donde ∆GV, ∆GB y ∆GS representan el cambio en la energía libre asociado con el volumen, con los bordes de
grano y con las superficies de los granos, respectivamente. La fuerza conductora principal en la sinterización
convencional es:
∆GS = γ∆S
(3.1.2)
es decir la que esta relacionada con las superficies de grano, pero los otros términos pueden ser significativos
en ciertos estados para algunos sistemas materiales.
3.2.- Energía de superficie.
La energía superficial especifica de un cuerpo viene dada por la expresión:
γ=
dETOT
dA
(3.2.1)
donde:
ETOT = Energia superficial de todo el cuerpo.
A = Superficie total de este.
Si el sólido es homogéneo, se tiene que:
ETOT = γ ∫ dA
(3.2.2)
Tomando como base esta definición, se puede deducir el aumento de energía superficial al pasar de un
sólido de notables dimensiones (cuya energía superficial puede considerarse despreciable) a un estado de
tamaño de partícula extremadamente pequeño.
 J 
En la tabla 3.2.1 se presentan los valores de energía superficial 
 del ClNa y del Al2O3 con la
 mol 
granulometría.
 J 
Tabla 3.2.1.- Variación de la energía superficial 
 del ClNa y del Al2O3 con la granulometría.
 mol 
Como puede observarse, los valores de energía superficial son inversamente proporcionales a las
dimensiones de las partículas (Energía superficial: Area superficial (1/D)), alcanzando valores apreciables
para tamaños de partícula próximos a 1 µm.
14
La fuerza conductora macroscópica de la sinterización es la reducción del exceso de energía asociado con las
superficies. Esto puede suceder por:
(1).- Reducción del área superficial total por un incremento en el tamaño promedio de las partículas, que
conducen a un incremento en el tamaño de la partícula (Figura 3.2.1.b),
y/o
(2).- Eliminación de interfases sólido/vapor y creación de áreas de borde de grano, seguido por crecimiento de
grano, que conduce a una densificación (Figura 3.2.1.a).
Se expresa como:
∆(γ A) = A∆γ + γ∆A
(3.2.3)
Donde:
γA = Energía interfacial total de un polvo
γ = Energía de superficie específica
A = Area total de la superficie
∆γ = Cambio en la energía de superficie específica debido a la densificación
El cambio en el área interfacial es debido al crecimiento de grano.
Los dos mecanismos anteriores están, usualmente, en competición. Si los procesos atómicos que conducen a
la densificación dominan, los poros se hacen más pequeños y tienden a desaparecer con el tiempo y el
material compactado contrae. Pero si los procesos atómicos que conducen al engrosamiento son más rápidos,
los poros y los granos se hacen más grandes con el tiempo.
Figura 3.2.1.- Dos de los caminos posibles por los que un conjunto de partículas puede disminuir su energía:
(a).- Densificación seguida de crecimiento de grano. En este caso ocurre contracción.
(b).- Engrosamiento, donde los granos crecen a expensas de los más pequeños.
En el caso de la densificación, las partículas esféricas cambian de forma, los centros de las partículas se
acercan y el volumen de la muestra decrecerá. El área superficial tiende a convertirse en área de borde de
grano. La energía de un borde de grano es menor que la energía de las dos superficies libres que son
eliminadas cuando se forma el borde y la energía total del sistema se reduce.
15
Una condición necesaria para que ocurra la densificación es que la energía de borde de grano γBG sea menor
que dos veces la energía superficial Sólido/Vapor, γSV . Esto implica que el ángulo diedral de equilibrio, Φ,
mostrado en la figura 3.2.2 y definido como:
Φ

2
γ BG = 2γ SV cos 
(3.2.4)
tiene que ser menor que 180°.
Figura 3.2.2.- Ángulo diedral de equilibrio entre el borde de grano y la interfase Sólido/Vapor.
Si una probeta contrae, su densidad disminuirá con el tiempo. Por consiguiente, la densificación se sigue
mejor por la medida de la densidad del material en función del tiempo de sinterización. Esto usualmente se
analiza mediante ensayos dilatométricos, donde la longitud de una probeta se mide en función del tiempo a
una temperatura dada. Curvas típicas de contracción se presentan en la figura 3.2.3 para dos temperaturas
diferentes T2 > T1.
La densidad del material en función del tiempo de sinterización, ρs, viene dada por:
ρs =
ρg
 ∆L 
1−

L0 

3
(3.2.5)
y la densificación, Ψ:
Ψ=
ρs − ρg
ρt − ρ g
(3.2.6)
donde:
ρg = Densidad de conjunto del polvo de partida
ρt = Densidad teórica del material.
16
Figura 3.2.3.- Curvas de contracción axial típica durante la sinterización en función de la temperatura, donde
T2>T1.
Otro método es la medida del tamaño relativo del cuello, x/D (Figura 3.2.4). El crecimiento de los cuellos
puede producir o no contracción (densificación), pero la reducción del area superficial aumenta
significativamente la resistencia mecánica de los compactos.
Figura 3.2.4.- Tamaño relativo del cuello,
x
D
En contraposición, si un compacto de polvo engruesa (se hace más grande), no se espera ninguna contracción
en un experimento dilatométrico. En tal caso, la cinética del engrosamiento es mejor seguida por la medida
del tamaño de partícula promedio como una función del tiempo vía microscopía electrónica de barrido.
Es útil representar el comportamiento resultante en gráficas que se conocen como curvas tamaño de grano en
función de la densidad, tal como y como se muestra en la figura 3.2.5. Típicamente un material seguirá el
camino asociado a la curva Y, donde la densificación y el engrosamiento ocurren simultáneamente. Sin
embargo para obtener densidades cercanas a la teórica, el engrosamiento tiene que suprimirse hasta que la
mayor parte de la contracción haya ocurrido, es decir, el sistema debe seguir la trayectoria denotada por la
curva Z.
Un polvo que sigue la trayectoria X, sin embargo, esta condenado a permanecer poroso –la energía libre se ha
consumido– ya que se han formado granos grandes, pero lo más importante también es que se han formado
grandes poros. Una vez formados, estos poros son cinéticamente muy difíciles de eliminar, y ellos pueden ser
aún termodinámicamente estables y en tal caso sería imposible eliminarlos definitivamente.
La densidad máxima se obtiene, pues, solamente cuando los procesos atómicos asociados con el
engrosamiento son suprimidos, mientras aquellos asociados con la densificación se mejoran.
17
Figura 3.2.5.- Trayectorias de tamaño de grano versus densidad para densificación (curva Z) y engrosamiento
(curva X). La curva Y presenta un polvo para el cual el engrosamiento y la densificación están
ocurriendo simultáneamente.
En el estado inicial, la energía superficial es igual al producto de la superficie total de las partículas que
constituyen el sistema multiplicado por la energía superficial específica de ellas ,γ , es decir:
Estado inicial :
(3.2.7)
ESi = γ ST = ( Para N partículas esféricas iguales )=γ 4π r 2N
En el estado final, esta energía corresponderá a la suma de las energías de las juntas de grano (de idéntica
naturaleza), de las juntas de fase (granos de naturaleza diferente) y de la asociada a la porosidad residual (Figura 3.2.6).
Figura 3.2.6.- La superficie de las partículas de la pieza en verde son reemplazadas, en la pieza sinterizada por
juntas de grano (Baja energía)
En la tabla 3.2.2 puede verse la energía superficial específica para distintas sustancias.
18
Tabla 3.2.2.- Energía superficial específica de varios materiales.
En el supuesto de que la energía correspondiente al estado final sea nula (sistema monocristalino 100 % denso),
se puede probar que, exceptuado el caso de sistemas integrados por partículas muy finas, el exceso de energía del
sistema asociado a la energía de superficie, es muy pequeño y, por tanto, no puede, por si sola, hacer
evolucionar el sistema, aunque si puede orientar su evolución con la cooperación fundamental de la
temperatura.
En la tabla 3.2.3 puede verse como se incrementa la superficie de una misma masa de partículas al ir
diminuyendo su tamaño.
Tabla 3.2.2.- Radio, área, volumen de la partícula, número de partículas y área total de cualquier disposición
de esferas después de n cortes, donde un corte se define como el reparto del material en
partículas cuyo radio es la mitad del valor de partida anterior.
19
20
3.3.- Diferencia de presión en una superficie curva. Ecuación de Laplace.
Si bien la fuerza conductora global que opera durante la sinterización es la reducción de la energía superficial,
esta se manifiesta localmente como diferencias de curvatura. En ausencia de una presión externa y de reacción
química, la curvatura de las superficies proporciona la fuerza motriz de la sinterización.
La tensión superficial es la causante de que en las superficies curvas exista una presión hidrostática a través
de la intercara. Así, la presión en la parte cóncava de la intercara es mayor que en la convexa. Suponiendo una
burbuja esférica de radio r (Figura 3.3.1), como la presión en el interior, P1, es mayor que la exterior, P2,
entonces la burbuja se expandirá Si la diferencia de densidad (y consecuentemente la fuerza de la gravedad)
es despreciable, la única resistencia que se opone a la expansión de la burbuja es el aumento de la
superficie al desarrollarse, es decir, el aumento de la energía superficial.
Figura 3.3.1.- Determinación de la presión de equilibrio necesaria para mantener una superficie esférica de
radio r.
En el equilibrio, el trabajo de expansión ∆ PdV debe ser igual al aumento de energía superficial γdA, con lo
que:
∆PdV = ( P1 − P2 ) dV = γ dA
Como A = 4π r 2 se tiene: dA = 8π rdr y
(3.3.1)
4
V = π r 3 se tiene: dV = 4π r 2dr , con lo que sustituyendo:
3
( P1 − P2 ) 4π r 2dr = γ 8π rdr
y simplificando:
∆P = P1 − P2 =
2γ
r
(3.3.2)
siendo:
γ = Energía superficial especifica o tensión superficial.
r = Radio de la esfera.
Dicha diferencia de presión es la causa de que un líquido ascienda por capilaridad, al insertarse un capilar en el
seno de éste. En la figura 3.3.2, la diferencia de presión debida a la energía superficial se equilibra con la
presión hidrostática de la columna de líquido.
21
Si el capilar es de radio R:
∆P =
2γ cos θ
= ρ gh
R
de donde:
γ=
ρ ghR
2 cos θ
(3.3.3)
Mediante la expresión (3.3.3) se puede determinar la energía superficial o tensión superficial del líquido conocido el
ángulo de contacto y la altura del líquido en el capilar.
h=
2γ cos θ
ρ gR
Figura 3.3.2.- Nivel del líquido en un capilar. El radio de curvatura de la superficie liquida es R/cosθ.
Si la superficie curva no es esférica también se puede relacionar la diferencia de presión con la curvatura
de la superficie.
La figura 3.3.3 nos muestra una porción ABCD de superficie curva, que se supone que se expande de forma
infinitesimal una cantidad dz, pasando a la nueva posición A’B’C’D’.
Figura 3.3.3.- Superficie curva que se expande
22
En el equilibrio, el trabajo de expansión ∆ PdV debe ser igual al aumento de energía superficial γdA, con lo
que:
∆PdV = γ dA
Pero:
dA = (x + dx)(y + dy) – xy = xy + xdy + ydx + dxdy – xy = xdy + ydx + dxdy
y despreciando las diferenciales de segundo orden:
dA = xdy + ydx
(3.3.4)
Como además:
dV = xydz,
se tiene:
∆P xydz= γ( xdy + ydx )
(3.3.5)
De la semejanza de triángulos de la figura 3.3.3 se deduce:
x + dx r1 + dz
=
x
r1
,
r1x + r1dx = r1x + xdz
de donde: ydx =
xydz
r1
y + dy r2 + dz
=
y
r2
,
r2 y + r2dy = r2 y + ydz
de donde: xdy =
xydz
r2
Sustituyendo estos valores de ydx y xdy en la expresión (3.3.5) se obtiene:
 xydz xydz 
∆Pxydz = γ 
+

r
r1 
 2
y simplificando:
1 1 
∆P = γ  +  
 r1 r2 
(Ecuación de Laplace)
(3.3.6)
Partícularizando la ecuación de Laplace, para algunas superficies partículares:
1.- Superficie esférica : r1 = r2 = r ,
∆P =
2.- Superficie cilíndrica: r1 = r , r2 = ∞ ,
∆P =
2γ
r
γ
r
3.- Superficie plana: r1 = r2 = ∞ , ∆P = 0
3.4.- Energía vinculada al exceso de vacantes que existe en la proximidad de las superficies cóncavas. Ecuación
de Kelvin-Thompson. Efecto de la curvatura sobre la concentración de vacantes.
En cualquier red cristalina, con o sin la presencia de átomos extraños, existen defectos puntuales de estructura. El más
simple de los defectos puntuales es la vacante, o vacante de red, lugar normalmente ocupado por un átomo
ahora ausente. Tales defectos pueden ser el resultado de un empaquetamiento imperfecto durante la
cristalización primaria (solidificación) o pueden originarse debido al aumento de las vibraciones térmicas de
los átomos a altas temperaturas que elevan la probabilidad individual de los átomos de saltar desde posiciones
de baja energía a alta, desplazándolos de sus posiciones reticulares normales. Son defectos de equilibrio,
termodinámicamente exigidos por la materia
23
En equilibrio, el número de vacantes, NV, de una cantidad determinada de material depende de la temperatura,
 Q 
NV = N exp  − V 
 kT 
(3.4.1)
En esta expresion, N es el número total de lugares ocupados por átomo, QV es la energía de activación (energía
vibracional requerida para la formación de una vacante), T es la temperatura absoluta en grados kelvin y k es
la constante Boltzmann. El valor de k es 1.38 x 10-23 J/átomosK, o 8.62 x 10-5 eV/átomo-K, dependiendo de las
unidades de QV. De este modo, el número de vacantes crece exponencialmente con la temperatura.
La formación de los defectos puntuales en un cristal requiere una aportación de energía considerable.
Esta energía esta en dependencia directa de la resistencia mecánica de los enlaces químicos y es proporcional
a la energía de enlace en eI cristal.
La introducción de defectos puntuales en un cristal aumenta su energía interna comparada con la del
cristal perfecto. Sin embargo, la energía libre del sistema no aumenta necesariamente sino que puede
disminuir. Esto puede verse a trabes del análisis de la ecuación:
∆G = ∆U − T ∆S
( 3.4.2 )
que nos relaciona la energía libre del sistema, G, con la energía interna , U y con el termino TS, (T =
Temperatura absoluta, S = Entropía). Aunque la energía interna U del sistema aumente, el valor de la
energía libre G puede disminuir debido al termino TS.
Para una temperatura determinada T, cuando el número de defectos aumenta la entropía S del cristal
se hace mayor a causa de que aumenta el número de posibles disposiciones. Así, el termino T ∆ S
aumentara, por consiguiente el valor de la energía libre puede disminuir a pesar del aumento de la energía
interna U. Cuando la adición de mas defectos al sistema ya no hace disminuir el valor de G, se ha alcanzado
el estado de equilibrio en el cual la energía libre ha alcanzado un mínimo, es decir la relación (3.4.2) es
mínima para una determinada concentración de defectos, la cual queremos determinar (Figura 3.4.1).
.
Figura 3.4.1.- Variación de la energía libre en función del número de vacantes
24
Supongamos un cristal con N puntos de red (posiciones atómicas), de las cuales NV están vacantes.
Admitamos que las vacantes se crean con arreglo al mecanismo propuesto por Schottky, en virtud del cual,
átomos del interior del cristal saltan a su superficie como indica la figura 3.4.2. Si llamamos QV a la energía
requerida para la formación de una vacante con arreglos a ese sistema, la energía interna del cristal que
contiene NV vacantes habrá aumentado en:
∆U = NV QV
( 3.4.3 )
Figura 3.4.2.- Mecanismo propuesto por Schottky para la creación de una vacante.
Busquemos ahora la variación de entropía. Esta ha de ser positiva pues la formación de vacantes va
acompañada de un aumento del grado de desorden de los átomos en el cristal. Dicha variación es
proporcional al número de maneras en que las vacantes pueden disponerse en el cristal y viene dada por:
SC = kLnW
(3.4.4)
donde:
k = Constante de Boltzmann
W= Probabilidad termodinámica, que representa el numero de procedimientos por los cuales
se puede realizar el estado del sistema
Para un cristal perfecto los N átomos, que son indistinguibles solamente se pueden disponer de una manera
en los N lugares reticulares , los cuales son distinguibles. Luego para el cristal perfecto el valor SC de
viene dado por:
SC1 = kLnW = kLn
O
O
O
O
O
O
O
O
O
O
O
O
O
O
N!
= kLn(1) = 0 luego: SC 1 = 0
N!
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
Para el cristal real las NV vacantes pueden distribuirse entre las N posiciones atómicas de:
CNNV =
N!
NV ! ( N − NV ) !
maneras.
25
O
O
O
O
O
O
O
V
O
O
O
O
O
V
O
O
V
O
V
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
V
O
O
O
O
V
O
O
O
O
O
O
O
O
O
O
O
O
Entonces el aumento de entropía de configuración como resultado de la disposición aleatoria de NV vacantes
es:


N!
SC 2 = kLnW = kLn 

 NV ! ( N − NV )! 
y la variación de entropía será:


N!
∆S = SC 2 − SC 1 = kLn 

 NV ! ( N − NV )! 
(3.4.5)
operando:


N!
∆S = SC 2 − SC 1 = kLn 
 = k [ Ln(N!)-Ln(NV !)-Ln(N!-NV !)]
 NV ! ( N − NV )! 
Suponiendo que N y NV son grandes se puede aplicar la aproximación de Stirling:
Ln(x!) = xLn(x) - x
con lo que:
∆S = k NLn(N ) − N − NV Ln(NV ) + NV − ( N − NV ) Ln ( N − NV ) + N − NV  =
= k NLn(N ) − NV Ln(NV ) − ( N − NV ) Ln ( N − NV ) 
(3.4.6)
Sustituyendo el valor de ∆U = NV QV dado por (3.4.3) y el de por (3.4.6) en la ecuación (3.4.2), se tiene:
∆G = NV QV − kT NLn(N ) − NV Ln(NV ) − ( N − NV ) Ln ( N − NV ) 
(3.4.7)
La energía libre aparece en función del número de vacantes, N V . A temperatura y presión constantes el
número de vacantes N V , en condiciones de equilibrio, ha de ser tal que haga mínima la energía libre G,
es decir debe cumplirse la condición:
 ∂∆G 

 =0
N
∂
 V P ,T
Por tanto, derivando con respecto a n la expresión (3.4.7) y operando nos queda:
 ∂∆G 

 = QV − kT  − Ln(NV ) − 1 + Ln ( N − NV ) + 1 = QV − kT  −Ln(NV ) + Ln ( N − NV ) 
 ∂NV P ,T
(3.4.8)
e igualando a cero:
QV − kT  −Ln(NV ) + Ln ( N − NV )  = 0
(3.4.9)
26
o bien:
QV
 N 
Ln  V  = −
kT
 N − NV 
de donde:
Q
NV
− V
= e kT
N − NV
(3.4.10)
y suponiendo que N es mucho mayor que N V , nos queda:
CV =
Q
NV
− V
= e kT
N
(3.4.11)
siendo CV la concentración de vacantes.
La expresión (3.4.11) se aplica, o es valida, a cualquier punto de un sólido cristalino limitado por una
superficie plana. Además, también se aplica rigurosamente a un volumen elemental, situado lejos de la
superficie del sólido. Si por el contrario, el volumen elemental esta situado cerca de la superficie, y ésta no es
plana, se podrá observar en las proximidades de ella, respecto a la concentración de vacantes C V en la
superficie plana, un exceso a defecto de estos ∆C, respecto a la concentración de equilibrio, que será
función del radio de curvatura de la superficie en la que se desea determinar ∆ C.
El valor de ∆C viene expresado por la ecuación de Kelvin-Thompson:
Si C = CV + ∆C entonces:
C
Ln 
 CV

γ Vm  1 1 
= −
 + 
RT  r1 r2 

(3.4.12)
donde:
γ = Energía superficial específica.
r1 , r2 = Radios de curvatura principales en el punto de la superficie considerado.
J
).
mol .K
Vm = Volumen ocupado por un mol de materia (Volumen molar)
R = kNA = Constante de los gases perfectos (= 8.3144
Vm = N AVa siendo NA el numero de Avogadro ( = 6x1023 átomos/mol y Va el volumen atómico.
En la formula (3.4.12), los radios de curvatura son positivos cuando apuntan hacia el interior de la fase
condensada y negativos en caso contrario.
Para demostrar la ecuación de Kelvin-Thomson supongamos que se llevan, a presión y temperatura constantes, dn
moles de vacantes desde una partícula limitada por una superficie plana hasta una limitada por una superficie
esférica de radio r (Figura 3.4.3).
27
Figura 3.4.3.- Aporte de dn moles de vacantes desde una partícula limitada por una superficie plana hasta una
limitada por una superficie esférica de radio r
La energía libre de la partícula plana disminuye en:
∆GPP = EV' dn
(3.4.13)
siendo:
E’V = Energía para formar un mol de vacantes en superficie plana
( = N AQN )
Por su parte, la energía libre de la partícula esférica aumenta en:
∆GPC = EV dn − γ dA
siendo:
(3.4.14)
EV = Energía para formar un mol de vacantes en superficie ( = N AQN )
γ = energía superficial específica.
dA = Variación del área
Igualando las expresiones (3.4.13) y (3.4.14) se tiene:
EV' dn = EV dn − γ dA
Como A = 4π r
2
se tiene:
EV' − EV = γ
dA = 8π rdr . Además
dA
dn
V 4π r 3
de donde:
n=
=
Vm
3Vm
(3.4.15)
4π r 2dr
dn =
.
Vm
Por tanto:
dA 8Vmπ rdr 2Vm
=
=
dn
4π r 2dr
r
y la expresión (3.4.15) se transforma en:
EV' − EV = −
2γ Vm
r
(3.4.16)
Por otra parte:
 N 
N
EV = N AQV = −N A kTLn  V  = −N A kTLn  V
N
 N − NV 
 N' 
N'
EV' = N AQV' = −N A kTLn  ' V '  = −N A kTLn  V'
N
 N − NV 

 = −RTLn(C )

 = −RTLn (CV )

28
Sustituyendo las expresiones anteriores en la (3.4.16):
RT [ Ln(C ) − Ln(CV ) ] = −
2γ Vm
,
r
C 
2γ Vm
RTLn   = −
r
 CV 
y finalmente:
C 
2γ Vm
Ln   = −
RTr
 CV 
(3.4.17)
En una superficie esférica los dos radios de curvatura principales son iguales al radio, r, de la superficie,
con lo que la curvatura media:
1  1 1  1 2
1
Cm =  +  =   =
2  r1 r2  2  r 
r
y la expresión (3.4.17) se transforma en:
C 
Ln   = − 2γ Vm Cm
RT
 CV 
(3.4.18)
y para una superficie curva no esférica:
γ Vm  1 1 
C 
Ln   = −
 + 
RT  r1 r2 
 CV 
(3.4.19)
Si aplicamos la formula anterior a dos partículas, supuestas esféricas, en proceso de sinterización (Figura 3.4.4) se
tiene:
Figura 3.4.4.-Mecanismo de sinterización simple dos esferas.
29
1.- En la proximidad de la zona de unión (puente),M,
γ Vm  1 1 
C 
Ln   = −
 − 
RT  x ρ 
 CV 
y como C = CV + ∆C y suponiendo x»ρ:
 C + ∆C 
 ∆C  γ Vm  1 
Ln  V
 = Ln  1 +
=
RT  ρ 
 CV 
 CV 
suponiendo CV»∆C se tiene que:
 ∆C  ∆C
Ln  1 +
≅
 CV  CV
con lo que:
γ Va
kT ρ
∆C γ Vm
=
=
CV
RT ρ
(3.4.20)
2.- En un punto cualquiera, N, de la superficie de las esferas:
r1 = r2 = r , Ln  1 + ∆C  = − 2γ Vm ,

CV 
RTr
∆C
CV
=−
2γ Va
kTr
(3.4.21)
Se concluye que en la proximidad de las superficies cóncavas (r<0) existe un exceso de vacantes, ∆C>0, y en
la proximidad de las superficies convexas (r>0)un defecto, ∆C<0, con respecto a la concentración de
vacantes en una superficie plana . Este exceso o defecto de vacantes, no es más que un gradiente de
concentraciones que originará un flujo (difusión) de vacantes desde las superficies cóncavas (cuellos) a las
convexas (partículas), a lo que corresponderá un flujo de átomos, de materia, en sentido contrario (difusión en
estado sólido).
Vamos a probar, mediante un ejemplo, que el exceso relativo de vacantes, presente en la vecindad de los puentes
entre partículas, es pequeño (salvo en los instantes iniciales de la sinterización). Luego este segundo
mecanismo, que haría posible la difusión en estado sólido, solo podrá guiar el proceso de sinterización con
ayuda de la temperatura. En efecto, es la activación térmica la que hace posible que las lagunas (átomos)
difundan y puedan eliminarse en "pozos" susceptibles de captar los defectos y de eliminarlos, sería de desear,
definitivamente (eliminación de la porosidad).
30
31
3.5.- Energía asociada a la existencia de una fase en estado vapor. Efecto de la curvatura sobre la presión.
El sistema aglomerado poroso considerado en un principio, comprende a parte de la fase (fases) sólidas, una
fase en estado vapor. Cuando la interfase sólido-vapor es plana, se puede definir, a cada temperatura, una
presión P0 de equilibrio entre ambos. Ahora bien, si la superficie (interfase) es curva, la presión del vapor en equilibrio
con el sólido, cambia en función de la curvatura de la superficie y toma el valor P1 establecido por la formula
de Gibbs-Thompson:
 P  γV  1 1 
Si P1 = P0 + ∆P
entonces: Ln  1  = m  + 
(3.5.1)
 P0  RT  r1 r2 
donde:
γ = energía superficial específica.
r1, r2 = Radios de curvatura principales en el punto de la superficie considerado.
R = kNA = Constante de los gases perfectos (= 8.3144 J/mol.K).
Vm =Volumen ocupado por un mol de materia (Volumen molar)
Vm = NAVa siendo NA el numero de Avogadro ( = 6x1023 átomos/mol y Va el volumen atómico.
En la formula (3.5.1), los radios de curvatura son positivos cuando apuntan hacia el interior de la fase
condensada; y negativos en caso contrario.
Para demostrar la ecuación de Gibbs-Thomson supongamos que se transfieren, dn moles de sustancia desde una
partícula limitada por una superficie plana hasta una limitada por una superficie esférica de radio r (Figura
3.5.1).
Figura 3.5.1.- Transferencia de dn moles de sustancia desde una partícula limitada por una superficie plana hasta
una limitada por una superficie esférica de radio r
El trabajo realizado en la transferencia, mediante la fase vapor, de esos dn moles de sustancia debe ser igual al
cambio de energía superficial, debido al aumento de superficie, es decir:
−W = γ dA
(3.5.2)
El trabajo se pone con signo menos ya que se ejecuta sobre el vapor.
32
Si la transferencia es isotérmica se tiene:
V2
W = ∫ PdV
V1
y como:
PV = dnRT
P=
,
dnRT
V
Se tiene:
V2
V1
W =∫
V 
V dV
dnRT
V
dV = RTdn ∫ 2
= RTdn [ LnV ]V2 = RTdnLn  2 
V1 V
1
V
 V1 
pero como:
P1V1 = P2V2
nos queda:
P
W = RTdnLn  1 
 P2 
y en nuestro caso:
P 
W = RTdnLn  0 
 P1 
Por otra parte, como A = 4π r 2 se tiene: dA = 8π rdr .
Sustituyendo los valores de W y dA en la expresión (3.5.2) se obtiene:
P 
− RTdnLn  0  = γ 8π rdr
 P1 
P
RTdnLn  1  = γ 8π rdr
 P0 
y operando:
 P  γ 8π rdr
Ln  1  =
 P0  RTdn
V
4π r 3
4π r 2dr
Además n =
=
de donde: dn =
Vm
Vm
3Vm
Sustituyendo:
 P  γ V 8π rdr
Ln  1  = m 2 ,
 P  RT 4π r dr
 0
 P  2γ Vm
Ln  1  =
 P0  RTr
(3.5.3)
En una superficie esférica los dos radios de curvatura principales son iguales al radio, r, de la superficie,
con lo que la curvatura media:
11 1 12 1
Cm =  +  =
=
2  r1 r2  2 r r
y la expresión (3.5.3) se transforma en:
 P  2γ Vm
2γ Va
Ln  1  =
Cm ==
Cm
 P  RT
kT
 0
(3.5.4)
33
y para una superficie curva no esférica:
 P  γV  1 1 
Ln  1  = m  + 
 P0  RT  r1 r2 
(3.5.5)
Si aplicamos la formula anterior a dos partículas, supuestas esféricas, en proceso de sinterización (Figura 3.5.2) se
tiene:
1.- En la proximidad de la zona de unión (puente),M,
 P  γV
Ln  1  = m
 P0  RT
1 1 
x − ρ


(3.5.6)
y como P1 = P0 + ∆ P y suponiendo x»ρ:
Suponiendo P0»∆P
 P + ∆P 
 ∆P 
γ Vm 1
Ln  0
 = Ln  1 +
=−
P0 
RT ρ
 P0 

 ∆P  ∆P
se tiene que: Ln  1 +
con lo que:
≅
P0  P0

γV
∆P
γV
=− m =− a
P0
RT ρ
kT ρ
(3.5.7)
o bien:
∆P = −
y como:
P0γ Vm
RT ρ
PoVm
= 1 , resulta finalmente:
RT
∆P = −
γ
ρ
(3.5.8)
Figura 3.5.2.-Mecanismo de sinterización simple dos esferas.
34
2.- En un punto cualquiera, N, de la superficie de las esferas:


r1 = r2 = r , Ln  1 + ∆P  = 2γ Vm ,

P0  RTr

∆P 2γ Vm 2γ Va
=
=
P0
RTr
kTr
(3.5.9)
de donde:
∆P =
2γ
r
(3.5.10)
Considerando la figura 3.5.2, la ecuación (3.5.10) nos indica que en las proximidades de una superficie
cóncava (r < 0) hay una disminución de la presión de equilibrio, mientras que en las proximidades de una
superficie convexa (r > 0) hay un aumento de la presión de vapor con respecto al de una superficie plana. Será, por
tanto, energéticamente favorable la transferencia del vapor de las superficies convexas (partículas) a las
cóncavas (cuello) en los procesos de sinterización. Luego, puede establecerse un transporte de materia, en fase
vapor, desde las superficies convexas hacia las cóncavas, mecanismo que se conoce con el nombre de
evaporación-condensación.
El efecto de la diferencia de presión de vapor de una superficie curvada respecto a la de una plana, así
como su variación con el tamaño de partícula aparece, para algunos sistemas, en la tabla 3.5.1.
Tabla 3.5.1.- Efecto de la curvatura superficial sobre la diferencia de presión y la presión de vapor relativa a
lo largo de la superficie curva.
El gran efecto del tamaño de partícula en estas relaciones es una de las bases de la utilización de los
minerales arcillosos en la tecnología cerámica o del pequeño tamaño de los polvos cerámicos. Sus finos tamaños de
partícula ayudan a los procesos de moldeo, ya que estos son una fuente de plasticidad, y aportan la energía
superficial suficiente al sistema para que se produzca la densificación adecuada en la cocción.
Resumiendo, las curvaturas causan variaciones locales en las presiones parciales y en las concentraciones de
vacantes. La presión parcial sobre una superficie convexa es más alta que sobre una superficie cóncava. A la
inversa, la concentración de vacantes bajo una superficie cóncava es más alta que bajo una superficie
convexa. En ambos casos, una fuerza conductora está presente lo que induce a los átomos a migrar de las
áreas convexas a las cóncavas, es decir, de los picos a los valles.
35
A lo largo de la superficie de las partículas las curvaturas cambian de positivo en la superficie de la partícula a
negativo en la región del cuello. Las regiones de curvatura positiva corresponden esfuerzos compresivos y
tendrán una presión de vapor más alta que en la superficie plana. A la inversa, regiones de curvatura negativa
tendrán un esfuerzo de tensión y una presión de vapor más baja que en la superficie plana. La diferencia de
presiones de vapor tiende a transportar materia a través de la fase de vapor a la región del cuello.
Las diferencias de esfuerzos tienden a transportar materia por difusión a la región del cuello. Ambos
mecanismos estarán activos y el crecimiento del cuello total será la suma de los dos procesos. El esfuerzo de
tensión en la región del cuello es balanceado por un esfuerzo compresivo en el borde de grano. Este esfuerzo
compresivo eleva la concentración de átomos en la región del borde de grano y el esfuerzo de tensión
disminuye la concentración de átomos en la región del cuello. Esta diferencia de concentración conduce al
transporte de materia de la región del borde de grano a la región del cuello por transporte en borde de grano y
transporte de red. En este caso, hay densificación del compacto.
3.6.- Presión externa aplicada.
En ausencia de reacción química, una presión externa aplicada normalmente constituye la contribución
principal a la fuerza motriz de la sinterización cuando la presión se aplica durante una parte significativa del
proceso de calentamiento, como es el caso del prensado en caliente, tanto uniaxial como isostático (Figura
3.1.1). La curvatura superficial también proporciona una contribución a la fuerza motriz, pero para la mayoría
de las situaciones prácticas es normalmente la contribución es mucho más pequeña que la proporcionada por
la presión externa. La presión externa trabaja sobre el sistema de partículas y, para 1 mol de partículas, el
trabajo realizado puede aproximarse mediante la expresión:
W = paVm
(3.6.1)
donde:
W = Fuerza motriz para la densificación debida a la aplicación de una presión externa.
pa = Presión externa aplicada.
Vm=Volumen molar.
Para pa = 30 MPa, que es una presión típica que se aplica en el prensado en caliente y Vm= 25x10-6 m3,
resulta:
W = 750 J
3.7.- Reacción química.
Una reacción química puede, en principio, proporcionar una fuerza motriz para la sinterización y puede
usarse para ayudar al proceso de densificación (Figura 3.1.1). El cambio de energía libre que acompaña a
una reacción química viene dado por:
∆G 0 = − RTLnK eq
(3.7.1)
donde:
R = Constante de los gases (8.314 J/mol).
T = Temperatura absoluta.
Keq = Constante de equilibrio de la reacción.
Tomando T = 1000 K y Keq =10, entonces ∆G°∼20000 J/mol. Esta disminución de la energía es
considerablemente mayor que la fuerza motriz debido a una tensión aplicada. En la práctica, una reacción
química casi nunca se usa deliberadamente para conducir el proceso de densificación en cerámicas avanzadas
debido a que el control de la microestructura se hace sumamente difícil cuando una reacción química tiene
lugar simultáneamente con la sinterización.
36
4.- Mecanismos de sinterización. Modelización del proceso de sinterización.
4.1.- Introducción.
La sinterización de materiales policristalinos ocurre por transporte de materia por difusión a lo largo de
caminos definidos que determinan los mecanismos desinterización. La materia se transporta de las regiones
de potencial químico más alto (Denominadas fuentes de materia) a las regiones de potencial químico inferior
(denominadas sumideros).
La forma como un material sinteriza depende de dos tipos de variables. La primera depende de:
1.- Material partida, incluyendo la composición química
2.- Tamaño y forma del polvo
3.- Distribución granulométrica del polvo
4.- Grado de sinterización, etc.
y afecta a la densificación y al crecimiento de grano.
La segunda es de tipo termodinámico y comprende:
1.- Temperatura y presión
2.- Tiempo
3.- Atmósfera
4.- Velocidad de calentamiento e enfriamiento
Después de haber considerado los tipos principales de fuerza motriz de la sinterización: exceso de energía
superficial, capilaridad, gradientes de presión vapor y concentración de lagunas en el sistema a sinterizar, se van a
examinar los distintos mecanismos de transferencia de materia propuestos para explicar el proceso de
sinterización. Los mecanismos de transporte se pueden clasificar en dos grupos:
1.- Tipo superficial (Difusión superficial y evaporación – condensación)
2.- Tipo “bulk” o global (difusión de bordes de grano, difusión en la red cristalina, flujo viscoso y flujo
de deformación plástica).
Los mecanismos de flujo viscoso y de deformación plástica no son importantes en los materiales cerámicos,
debido a los enlaces iónicos que lo impiden. Los mecanismos de flujo viscoso y de deformación plástica son
efectivos cuando está presente un líquido que moja o cuando se aplica una presión mecánica, respectivamente.
Según la forma en que se transfiere la materia estos mecanismos se clasifican en:
Tipo sinterización
Mecanismo de transporte de materia
Fase vapor
Evaporación – condensación
Fase sólida
Fase líquida
Mecanismos de difusión atómica
- Difusión superficial
- Difusión en volumen
- Difusión intergranular
Difusión y flujo viscoso
Fase líquida reactiva
Flujo viscoso y solución – precipitación
Fuerza motriz.
Exceso de presión
(Diferencias en la presión
vapor)
Exceso de vacantes
Exceso de energía
superficial.
Exceso de energía
superficial
37
Así mismo, en la tabla 4.1.1 y en la figura 4.1.1 pueden verse, más detalladamente, los mecanismos de
transporte de materia en estado sólido por difusión, alternativos al mecanismo de evaporación –
condensación. Se puede observar que existen, al menos, seis mecanismos diferentes para la sinterización de
materiales policristalinos. Todos ellos conducen a la unión y crecimiento de los cuellos entre las partículas,
de tal modo que la resistencia del compacto de polvos aumenta durante la sinterización.
Sin embargo, sólo ciertos mecanismos conducen a la contracción o densificación, y así se hace una distinción
entre los mecanismos que densifican y los que no densifican. La difusión superficial, la difusión de red de las
superficies de las partículas al cuello y el transporte de vapor (mecanismos 1, 2, y 3) conduce al crecimiento
de cuello sin producir densificación y se denominan mecanismos que no densifican. La difusión por el límite
de grano y la difusión de red desde el límite de grano hacia el poro (mecanismos 4 y 5) son los mecanismos
que densifican más importantes en las cerámicas policristalinas.
El flujo plástico por el movimiento de las dislocaciones (mecanismo 6) también conduce a la crecimiento del
cuello y a la densificación, pero es un mecanismo más común en la sinterización de polvos metálicos.
Para los materiales amorfos (vidrios), que no tienen fronteras de grano, el crecimiento del cuello y ls
densificación ocurren por flujo viscoso, el cual implica la deformación de las partículas.
Tabla 4.1.1.- Mecanismos de transporte de materia en estado sólido p o r d i fu si ón , al t ern at iv o al d e
ev ap o ració n -con d ens ació n .
N°
Mecanismo
Mecanismo
de transporte
Origen de
Materia
Destino de la
Materia
Contraccion
(Eliminacion
de Porosidad)
1
Difusion superficial
Superficie
Puente de union
NO
Superficie
Puente de union
NO
Junta de
grano
Puente de union
SI
Junta de
grano
Puente de unión
SI
Dislocaciones
Puente de unión
SI
2
3
4
5
Difusión a través de
la red cristalina
(VOLUMEN)
Difusión a través de
los bordes de grano
(INTERGRANULAR)
Diffusion a través de
la red cristalina
(VOLUMEN)
Diffusion a través de
la red cristalina
(VOLUMEN)
Es importante apreciar, en principio, que cualquier mecanismo en que la fuente de materia sea la superficie de
las partículas y el sumidero el área del cuello no puede conducir a densificación, porque tal mecanismo no
permite que los centros de las partículas se acerquen. Consecuentemente, evaporación-condensación, difusión
superficial, y difusión en red de la superficie al área del cuello no puede conducir a densificación. Estos, sin
embargo, resultan en un suavizado de las superficies, en un cambio en la forma de los poros (Redondeo de los
poros), un crecimiento en el tamaño del cuello (Unión de las partículas), y un incremento simultáneo en la
resistencia del compacto.
La difusión superficial es la que se presenta en muchos sólidos covalentes. Las cerámicas que presentan el
mecanismo de evaporación-condensación son las de baja estabilidad.
38
Por otra parte, los granos más pequeños, con sus radios de curvatura más pequeños, tenderán a “evaporarse” y
recubrir a las partículas más grandes, resultando en un engrosamiento de la microestructura.
Teórica y experimentalmente se ha podido comprobar que la difusión superficial es el mecanismo mas
importante durante los primeros estados de la sinterización (recordemos que mediante este mecanismo solo
crece el área del cuello entre las partículas sin afectar a la contracción y a la porosidad. Por su parte, la difusión
en volumen y la difusión intergranular se van hacienda más efectivas conforme avanza la sinterización.
Figura 4.1.1.- Mecanismos de transporte de materia durante las etapas de la sinterización.
39
Figura 4.1.1.- Mecanismos de transporte de materia durante las etapas de la sinterización.
40
En la figura 4.1.2 puede verse en detalle el mecanismo de difusión a través de las juntas de grano del puente
formado hacia el hueco (Poro), que van rellenando. Las juntas de grano, desde el punto de vista atómico,
son partes “debiles” y la difusión tiene lugar con más facilidad, por lo que este mecanismo es el más
efectivo. Debido a que se elimina materia de las juntas de grano las partículas de aproximan y, por tanto,
tiene lugar una densificación.
Figura 4.1.2.- Mecanismo de transporte de materia junta de grano – hueco.
La difusión en borde de grano es un mecanismo que está considerado entre los más importantes para la
mayoría de los sólidos cristalinos y controla la densificación de muchos materiales cerámicos, incluyendo a la
alúmina.
Cada mecanismo puede operar solo o en combinación con otros, al objeto de acelerar y aumentar la
densificación del sistema aglomerado poroso. El que uno o varios de estos mecanismos contribuyan en forma
apreciable al proceso de sinterización depende de las velocidades relativas de cada uno de estos.
Una de las diferencias mas significativas entre los distintos mecanismos es que la transferencia de materia de la
superficie de la partícula por difusión superficial, difusión en volumen y evaporación - condensación, no reduce la
distancia entre los centros de las partículas; por lo que las dimensiones y la porosidad de la muestra no cambian a
lo largo de todo el proceso, es decir, solo varía la forma de los poros. A diferencia de estos mecanismos la
sinterización por los mecanismos de flujo viscoso, deformación plástica, difusión intergranular y difusión en volumen
del interior del grano, además de cambiar la forma de los poros, varían la porosidad y las dimensiones de la
pieza que sinteriza.
El estudio de los mecanismos de sinterización nos permitirá obtener las ecuaciones cinéticas del proceso y la influencia de las distintas variables que lo afectan. Para ello necesitaremos recurrir a modelos más o menos simplificados
que nos permitan disminuir las dificultades de carácter geométrico que entrañaría el tratamiento de sistemas
reales.
La cinética de la sinterización es más compleja que determinar sólo el mecanismo de transporte más rápido,
debido a que depende además de muchas variables, que incluyen el tamaño y empaquetamiento de las
partículas, la atmósfera de sinterización, el grado de sinterización, la temperatura, y la presencia de impurezas.
Por simplicidad, el análisis se limitará a un modelo de dos esferas de gran radio inicialmente tangentes y que
progresivamente, al avanza la sinterización y crecer el cuello, se vuelven secantes. Este modelo será el utilizado en
las etapas iniciales e intermedias de la sinterización. En la etapa final (formación de porosidad cerrada) el sistema se
representará por un conjunto de poros esféricos y de igual tamaño incluidos en el interior del material.
41
La presencia de los límites de grano en los materiales policristalinos dicta las formas de equilibrio de los
granos y de los poros en dichos materiales.
Consideremos un poro hipotético rodeado por tres granos como se muestra en la figura 4.1.3. Las fuerzas
deben equilibrarse en la unión donde las superficies de los poros encuentran el límite de grano. Normalmente
están representadas por la tensión en la intercara, por ejemplo, la tensión en la intercara vapor-sólido y la
tensión en el límite de grano. Por analogía con la tensión superficial de un líquido, surge una tensión ya que
un aumento del área de la intercara conduce a un aumento de la energía. En la unión, la tensión en la
intercara vapor- sólido es tangencial a aquella intercara, mientras en el límite de grano está en el plano del
límite. El equilibrio de fuerzas conduce a la expresión:
Ψ

2
γ gb = 2γ gb cos 
(4.1.1)
donde:
Ψ = Ángulo diedral
En la mayoría de los modelos de sinterización se asume que los poros tienen una sección transversal circular,
lo que es equivalente a suponer que Ψ = 180 º o γgb = 0.
Figura 4.1.3.- Forma de equilibrio de los poros en sólidos policristalinos, la cual esta gobernada por el balance
entre las fuerzas de superficie e interfaciales en el punto donde el limite de grano interfecta con
el poro. γSV es la energía específica superficial , γgb es la energía específica del limite de
grano y Ψ es el ángulo diedral
En la sinterización de materiales policristalinos, parte de la disminución de energía debida a la eliminación de
área de la superficie libre se emplea en crear nueva área de límite de grano (Figura 4.1.1), entonces la fuerza
motriz para la sinterización será algo inferior a la calculada mediante la ecuación:
ES =
3γ SV Vm
a
, a = Radio de la partícula, Vm = Volumen molar
(4.1.2)
donde se desprecian las fronteras de grano.
42
Si ∆ASV y ∆Agb son los cambios del área de la superficie libre y del área de límite de grano, respectivamente,
entonces el cambio de la energía del sistema es:
∆E = γ SV ∆ASV + γ gb ∆Agb
(4.1.3)
donde γSV es la energía específica superficial y γgb es la energía específica del límite de grano. El sistema
evolucionará hacia un equilibrio provisional gobernado por la condición:
γ ∆A
gb
gb
=
γ
>
γ
SV
∆A
(4.1.4)
∆A
(4.1.5)
SV
Hay que señalar también que cuando:
γ ∆A
gb
gb
SV
SV
el cambio de energía ∆E dado por la ecuación (4.1.3) es positivo. En estas condiciones, hay un incentivo para
que el área de la superficie vapor-sólido aumente, es decir para que los poros crezcan. Los modelos de
sinterización asumen, comúnmente, un sistema en el que el polvo esta uniformemente empaquetado en el cual
los poros disminuyen de tamaño durante la sinterización. En el análisis del crecimiento de poro hay que
considerar las interacciones de los poros con las fronteras de grano.
Quizás una de las consecuencias más importantes de la presencia de las fronteras de grano es que el
crecimiento de grano proporciona un proceso alternativo por el cual el sistema de polvo puede disminuir su
energía (reduciendo la energía total de límite de grano). El crecimiento de grano normalmente esta
acompañado por el crecimiento de poro, en un proceso global que se denomina “coarsening”, el cual tiene
lugar simultáneamente con la sinterización.
4.2.-Modelos analíticos para la etapa inicial de la sinterización.
4.2.1.- Introducción. Parámetros geométricos.
Los modelos analíticos asumen una geometría idealizada simple del sistema de polvo y para cada mecanismo
se resuelven las ecuaciones del transporte de masa proporcionándonos las ecuaciones cinéticas de la
sinterización. Una dificultad es que la microestructura del compacto real de polvo cambia de forma continua
durante la sinterización. Es, por lo tanto, difícil de encontrar un modelo geométrico simple que represente
suficientemente todo el proceso. Para solucionar este problema, el proceso de sinterización conceptualmente
se divide en etapas separadas, y para cada etapa, se asume una geometría idealizada que tiene una semejanza
aproximada con la microestructura del sistema en polvo.
Los modelos analíticos, comúnmente, asumen que las partículas del polvo inicial son esféricas y del mismo
tamaño y que están uniformemente empaquetadas. Con estas asunciones, una unidad del sistema en polvo,
llamada modelo geométrico, puede ser aislada y analizada. Imponiendo las condiciones límite apropiadas, el
resto del sistema en polvo puede ser considerado como un continuo que tiene las mismas propiedades
macroscópicas (por ejemplo, contracción y velocidad de densificación) que la unidad aislada. La derivación
de las ecuaciones para la cinética de la sinterización sigue un procedimiento simple: para el modelo
geométrico asumido, se formulan las ecuaciones del transporte de masa de transporte y se resuelven con las
condiciones límites apropiadas.
El modelo para la etapa inicial de la sinterización consiste en dos esferas de igual tamaño en contacto, y se
denomina como el modelo de las dos esferas. Pueden considerarse dos geometrías ligeramente diferente,
dependiendo de que los mecanismos no den lugar a la densificación (Figura 4.2.1.1.a) o si den lugar a la
43
densificación (Figura 4.2.1.1.b). El modelo de las dos esferas para los mecanismos que densifican tiene en
cuenta la interpenetración de las esferas (Contracción), así como el crecimiento de cuello.
El cuello formado entre las partículas se asume que es circular con un radio X y con una superficie que tiene
una sección transversal circular con un radio r. Una sección transversal circular para la superficie de cuello es
equivalente a asumir que la energía del límite o frontera de grano es cero.
Los principales parámetros geométricos del modelo son los radios de curvatura principales de la superficie del
cuello r y X, el área de la superficie del cuello A y el volumen de material transportado hacia el cuello V.
Estos parámetros se resumen en la figura 4.2.1.1.
Figura 4.2.1.1.- Parámetros geométricos para el modelo de dos esferas usado en la derivación de las
ecuaciones de la etapa inicial de la sinterización de partículas cristalinas. (a).- Mecanismos
que no densifican (b).- Mecanismos que densifican
4.2.2.- Sinterización en fase vapor. Mecanismo de evaporación - condensación.
La sinterización en fase vapor solo es importante en procesos efectuados a elevada temperatura, próxima a la de
fusión de las partículas que constituyen el aglomerado poroso.
La fuerza motriz de este mecanismo de sinterización, es decir la tendencia a la transferencia de materia en
fase vapor, reside en las diferentes curvaturas de las superficies y, por tanto, en las diferencias de presión de
vapor en las distintas partes del sistema de polvos (superficies curvas cóncavas y convexas).
Conforme se indica en la figura 4.2.2.1, existe un transporte de materia, en fase vapor, desde la superficie de
las partículas con curvatura convexa (Superficie de la esfera) donde:
( ∆P )e =
2γ
( > 0)
r
hacia las zonas de contacto de las mismas (zona de formación de puentes) con curvatura cóncava donde:
( ∆P )c = −
γ
ρ
(< 0)
Hay, por tanto, una tendencia a la transferencia de materia en fase gaseosa de la superficie de la esfera a la
superficie del cuello, que contribuye a su crecimiento.
44
Cuanto mas pequeñas son las partículas, mayor es la fuerza motriz para la sinterización en fase vapor. En la
tabla 4.2.2.1 se recoge, en función del tamaño de las partículas que constituyen el aglomerado, el incremento de
la presión de vapor en sistemas de alumina y magnesia respectivamente.
Tabla 4.2.2.1.- Incremento de la presión de vapor en sistemas de alúmina y magnesia.
2γ
γ Al2O3 = 900 erg/cm 2 , γ MgO = 1100 erg/cm2
( ∆P )e =
r
r (µm)
0.1
1
10
100
( ∆P ) Al2O3
180 atmósferas
18 atmósferas
1.8 atmósferas
0.18 atmósferas
( ∆P )MgO
240 atmósferas
24 atmósferas
2.4 atmósferas
0.24 atmósferas
Es importante hacer notar que la sinterización en fase vapor cambia la forma de los poros pero no su volumen.
Enlaza "químicamente" las partículas, aumentando la resistencia del aglomerado, pero no produce su
densificación por contracción de la masa porosa. Por lo tanto, deberán existir mecanismos complementarios de
transporte de materia o de poros hacia la superficie externa del aglomerado, que hagan posibles su
densificación.
La ecuación cinética del proceso se obtendrá igualando la velocidad de condensación en el cuello con el
aumento de volumen de este. La transferencia de materia en fase vapor (evaporación - condensación) es
importante solo para unos pocos sistemas. Sin embargo, es el mecanismo más simple de tratar
cuantitativamente.
Figura 4.2.2.1.- Mecanismo de sinterizacion en fase vapor por evaporación – condensación.
45
La velocidad de condensación en la superficie del cuello es proporcional a la diferencia de presión entre la
superficie del cuello y la superficie de la partícula, y viene dada por la ecuación de Langmuir:
 M 
m = α∆P 

 2π RT 
donde:
1
g
cm 2 .s
2
(4.2.2.1)
g
m = Flujo de materia por unidad de superficie cm 2 .s
α = Coeficiente de acomodación, que, aproximadamente vale 1.
∆P = diferencia de presión de vapor entre la superficie del cuello y la superficie de la partícula que puede
considerarse plana.
∆P =
Po γ Vm
RT ρ
y como Vm =
M
d
(M = Peso molecular del vapor) , ∆P =
Poγ M
RTd ρ
(4.2.2.2)
Por otra parte, la velocidad de condensación sobre la superficie S del cuello es igual a la acumulación de
materia en el cuello, dV/dt, esto es:
mdA dV
cm 3
=
(4.2.2.3)
d
dt
s
De la geomet.ría de las dos esferas en contacto (Figura 4.2.2.2) , se obtienen para el radio (p), el area (A) y
volumen del cuello, V, las siguientes expresiones:
ρ=
x2
2r
,
A=
π 2x 3
r
,
V=
π x4
2r
(4.2.2.4)
Figura 4.2.2.2.- Geometría de dos esferas en contacto
46
siempre que
donde :
x
≤ 0.3
r
2π x = Longitud de la circunferencia que describe el arco de semicircunferencia
πρ = Longitud de la semicircunferencia
Sustituyendo en la ecuación (4.2.2.3) las ecuaciones (4.2.2.1), (4.2.2.2) y (4.2.2.4), se obtiene:
1
2 3
d π x 4 
 M  2π x
∆P 
= 


dt  2r  ,
 2π RT  dr
Poγ M  M 


RTd ρ  2π RT 
Poγ M  M 


 x 2   2π RT 
RT   d
 2r 
1
2
π 2x 3
dr
=
1
2
π 2x 3
dr
=
d π x 4 


dt  2r 
d π x 4 


dt  2r 
operando se llega a:
 M 
x dx = 

 2π RT 
2
1
2
π r γ Po M
RTd 2
dt
(4.2.2.5)
integrando (4.2.2.5), se llega a la ecuación cinética:
x 2
x dx
0
∫
x3  M 
=

3  2π RT 
1
2
 M 
=

 2π RT 
π r γ Po M
RTd
2
t
,
1
2
π r γ Po M
RTd 2
x3
t
∫0 dt
 M 
= 3

3
r
 2π RT 
1
2
πγ Po M
RTd 2r 2
t
de donde:
3
x  3 π γ M 2 P0  − 2 3 13
r t
=
r  2R 3 2T 3 2 d 2 


(4.2.2.6)
47
La expresión (4.2.2.6) nos relaciona el diametro (x) de la superficie de contacto entre las partículas (cuello) con las
variables que le afectan. Predice que la velocidad de la región del cuello:
(1).- Es inicialmente bastante rápida pero luego disminuye,
(2).- Es fuertemente dependiente del tamaño de partícula inicial, y
(3).- Es dependiente de la presión parcial P0 = PS. PLANA del compuesto, que a su vez depende
exponencialmente de la temperatura.
Así, las principales variables, además del tiempo, que afectan a la sinterización por este mecanismo son: el
2/3
radio inicial de la partícula (velocidad proporcional 1/r ) y la presión de vapor (velocidad proporcional
1/3
P0 ).
La importancia de la determinación de x radica en que la resistencia mecánica, conductividad térmica y eléctrica y
otras propiedades del sistema, están relacionadas con el valor del parámetro x/r.
En la figura 4.2.2.3 se ha representado x/r en función del tiempo de sinterización, en escala lineal y logaritmica
para el ClNa a 725°C. Se observa una disminución de la velocidad de crecimiento de cuellos (x/r) con el tiempo de
sinterización como predice la ecuación cinética.
Figura 4.2.2.3.- Representación lineal (a) y doble logaritmica (b) del crecimiento del cuello entre partículas
esféricas de cloruro sódico a 275°C.
Si se observan los cambios en la estructura que tienen lugar en la sinterización por este mecanismo, aparece
claramente que la distancia entre los centros de las partículas (Figura 4.2.1) no cambia, y por tanto no tiene lugar una
contracción de la pieza ni una reducción de la porosidad total de la misma, solo cambia la forma de los
poros. Este cambio de forma de los poros puede tener una apreciable influencia sobre las propiedades, pero
no afecta a la densidad.
Debido a que la presión de vapor aumenta exponencialmente con la temperatura, la sinterización par este
mecanismo es altamente dependiente de la temperatura.
Son, por tanto, el tamaño de partícula inicial y la temperatura de cocción (que fija la presión de vapor) para un material determinado, las variables que fundamentalmente controlan el proceso.
La transferencia de materia en fase vapor, requiere que los materiales se calienten a una temperatura suficientemente alta para que la presión de vapor sea apreciable.
Para tamaños de partícula del orden de 1 µm las presiones de vapor requeridas son de 10-4 a 10 -4 atmósferas.
Presiones más altas que éstas se encuentran usualmente durante la sinterización de óxidos y otros sistemas cerámicos.
48
4.2.3.- Sinterización en fase sólida. Mecanismos de difusión atómica.
4.2.3.1.- Introducción.
El transporte difusional de materia, puede ser analizado en términos de flujo de átomos o equivalentemente en
términos del contraflujo de vacantes. En el desarrollo inicial de la teoría de la sinterización, se usó
predominantemente la aproximación basada en el contraflujo de vacantes conducido por un gradiente de
concentración de vacantes, pero tambien se puede trealizar la aproximación general basada en el flujo de
átomos conducidos por un gradiente del potencial químico. Así, la sinterización puede ser vista en términos de
difusión de átomos o de vacantes.
La diferencia de energía libre o potencial químico entre el área de cuello y la superficie de la particula causa
la transferencia de materia por el mecanismo de difusión más rápido posible. La sinterización en fase sólida
tiene lugar por el mecanismo de difusión, es decir, por el transporte térmicamente activado de átomos (vacantes).
La materia puede difundirse de la superficie de la partícula, del interior de la partícula y de la zona intergranular
(GRAIN BOUNDARY) por difusión superficial, difusión en volumen o difusión intergranular. (Tabla 4.2.3.1.1 y
figura 4.2.3.1.1).
Tabla 4.2.3.1.1.- Formas alternativas para el transporte de materia por difusión en el estado inicial de la
sinterización.
Forma de transporte
Fuente de la materia Destino de la materia
1.- Difusión superficial
Superficie
Cuello
2.- Difusión en volumen
Superficie
Cuello
3.- Difusión intergranular
Frontera de grano
“Grain boundary”
Cuello
4.- Difusión en volumen
Frontera de grano
“Grain boundary”
Cuello
5.- Difusión en volumen
Interior del grano
Cuello
49
Figura 4.2.3.1.1.- Formas alternativas para el transporte de materia por difusión en el.-estado inicial de la
sinterización
El que uno o varios de estos mecanismos contribuya significativamente al proceso de sinterización de un sistema
en particular depende de sus velocidades relativas.
Teórica y experimentalmente se ha podido comprobar que la difusión superficial es el mecanismo más
importante durante los primeros estados de la sinterización y que mediante este mecanismo sólo crece el área del
cuello entre las partículas sin afectar a la contracción y a la porosidad. La difusión en volumen y la difusión
intergranular se van hacienda más efectivas conforme avanza la sinterización.
La difusión a través de la red tiene lugar por el movimiento de los defectos puntuales a través de ella.
Dependiendo del tipo de defectos (Vacantes o intersticiales), la difusión a través de la red puede tener lugar
por el mecanismo de vacantes o el intersticial (Figura 4.2.3.1.2)
Un átomo en un sitio de red normal cambia su lugar con una vacante (Figura 4.2.3.1.2.a). El movimiento del
átomo es opuesto al de la vacante, entonces se puede seguir el movimiento del átomo (por ejemplo, la
difusión de átomo) o, equivalentemente, el movimiento de la vacante (difusión de vacante). Los coeficientes
de difusión de los átomos y de las vacantes están relacionados, pero no son iguales. Un átomo sólo puede
saltar si una vacante está localizada sobre un sitio de red adyacente, pero una vacante puede saltar a cualquiera
de los sitios ocupados vecinos más cercanos. El número de saltos atómicos por lo tanto será proporcional a la
fracción de sitios ocupados por las vacantes, CV. El coeficiente de difusión atómica Da y el coeficiente de
difusión de las vacantes DV, estan relacionados por la expresión:
Da = CV DV
(4.2.3.1.1 )
La concentración de vacantes esta determinada por la temperatura, el soluto, y la atmósfera. En la difusión de
vacantes, el flujo de puestos vacantes debe ser compensado por un flujo igual y opuesto de átomos. De otra
manera, los puestos vacantes se acumularían en el cristal y producirían e poros.
Si son lo bastante pequeños, los átomos soluto o los átomos regulares a menudo pueden encontrarse en los
sitios intersticiales de la red y moverse a sitios intersticiales vecinos (Figura 4.2.3.1.1.b). Se tendrá una
relación análoga a la ecuación (4.2.3.1.1) :
Da = Ci Di
(4.2.3.1.2)
donde Di es el coeficiente de difusión intersticial y Ci la concentración de los átomos intersticiales.
50
Figura 4.2.3.1.2.- Difusión a través de la red. (a).- Mecanismo de vacantes, (b).- Mecanismo intersticial,
(c).-Intersticialmente (d).- Mecanismo de anillo
En los materiales policristalinos, los cristales o granos están separados unos de otros por regiones con
desajustes y desorden de la red, denominadas fronteras de grano. A causa de la naturaleza sumamente
defectuosa del límite de grano, es de esperar que la difusión en el límite de grano sea más rápida que la
difusión en la red en los granos adyacentes. Aunque no se conoce con exactitud, la anchura de la región de
límite de grano se asume que es de 0.5-1 nm. Para una anchura de límite de grano constante, la fracción de
sólido que ocupan los límites de grano aumenta cuando disminuye el tamaño de grano, de tal modo que la
velocidad de difusión en el límite de grano promediada de varios granos depende del tamaño de grano.
La superficie libre de un sólido cristalino no es perfectamente plana (Figura 3.19 4.2.3.1.3), sino que contiene
algunas vacantes (como el cristal global), terrazas, torceduras, bordes, y adatoms. La migración de las
vacantes y el movimiento de adatoms proporciona los mecanismos principales de difusión superficial. El
proceso de difusión se asume que esta limitado a la delgada capa superficial que tiene un espesor de 0.5-1 nm.
Figura 4.2.3.1.3.- Modelo de superficie sólida heterogénea mostrando diferentes defectos superficiales.
51
La fuerza motriz de la sinterización en fase sólida es el gradiente de concentración de vacantes que se establece
entre puntos próximos a superficies con diferente curvatura.
Basándonos en la ecuación:
γV
∆C γ Vm
=
= a
CV RT ρ kT ρ
en las proximidades de la superficie del cuello hay un exceso de vacantes respecto a la concentración de
equilibrio .
Por el contrario, en las proximidades de la superficie de la esfera, alejado del cuello, existe un defecto de
vacantes:
2γ Va
∆C
=−
CV
kTr
Así mismo, en el centro de los puentes existe una concentración próxima a la de equilibrio
En la figura 4.2.3.1.4 se muestra un esquema que ilustra la dirección del flujo de vacantes en una
superficie curvada, con una superficie convexa y cóncava adyacentes. El flujo de átomos es igual y
opuesto al de las vacantes.
Figura 4.2.3.1.4.- Esquema que ilustra la dirección del flujo de vacantes en una superficie curvada. El
flujo de átomos es igual y opuesto al de las vacantes.
4.2.3.2.- Mecanismo de difusión superficial.
En el mecanismo de difusión superficial se puede suponer que las vacantes en exceso se difunden, por ejemplo
superficialmente, del cuello a la superficie de la esfera (Figura 4.2.3.2.1). Si se establece un flujo de vacantes,
existirá en sentido inverso un flujo equivalente de átomos, desde áreas cercanas al cuello hacia el área del
cuello, que contribuye a llenar el cuello, limitado a un estrato superficial de espesor δS (del mismo orden del
diámetro atómico de los átomos que constituyen la esfera).
52
Figura 4.2.3.2.1.- Mecanismo de sinterización por difusión. Mecanismo de difusión superficial.
La ecuación cinética del proceso se determina al igualar la variación de volumen del cuello por unidad de tiempo
con el flujo de átomos que penetran en el mismo (que será equivalente al flujo de vacantes que abandonan el
cuello), es decir,
dV
= Je A
dt
(4.2.3.2.1)
siendo Je el flujo de vacantes que abandonan el cuello por unidad de superficie y de tiempo y A la superficie
atravesada por el flujo de vacantes. Por simplicidad, y suponiendo la simetria del sistema, la superficie la
consideraremos como una corona circular de radio x y de espesor δS.
El flujo de vacantes se puede expresar matemáticamente con la primera ley de Fick, teniendo presente que, por
simetria, la mitad de las vacantes se dirigen a la superficie de una esfera y la otra mitad a la otra. Considerando
que el gradiente de lagunas está limitado a una distancia x1 de la sección media de A, la ley de Fick se escribe:
Je
∆C
= −D
2
x1
donde D es el coeficiente de difusión de las vacantes y
(4.2.3.2.2)
∆C
es el gradiente de concentración de las vacantes.
x1
53
4.2.3.3.- Mecanismo de difusión en volumen.
En el mecanismo de difusión en volumen, al igual que el anterior está basado en la existencia de un exceso de
lagunas próximas a la superficie del cuello y de un defecto de vacantes en las proximidades de la superficie de la
esfera y lejos del cuello. La única diferencia con respecto al mecanismo anterior es que la difusión tiene lugar en el
volumen de la esfera.
El método de cálculo para obtener la ecuación cinética es similar al anterior.
En la difusión intergranular las vacantes se difunden de la superficie del cuello a la zona intergranular, o lo que es lo
mismo existe un flujo atómico en el sentido contrario, que produce una contracción al aproximarse.
4.2.3.4.- Mecanismo por difusión en volumen, desde el borde de grano al cuello.
El transporte de materia se produce desde la frontera, límite o borde de grano (GRAIN BOUNDARY) al cuello
por difusión en volumen. El cálculo de la ecuación cinética de este proceso es exactamente análogo a la
determinación de la velocidad de sinterización en fase vapor. La velocidad con que se difunde la materia del límite
de grano es igual a la acumulación de materia en el cuello.
La geometría del modelo, esferas secantes (Figura 4.2.3.4.1 ) no es igual a la del mecanismo de evaporación –
condensación donde las esferas eran tangentes.
Figura 4.2.3.4.1.- Modelo para el proceso de sinterización. Dos esferas de radio r han sinterizado para formar
una superficie de contacto de radio x, en la interfase aparece una superficie lenticular de radio
ρ y los centros de las esferas se han acercado una distancia ∆L.
En este caso se tiene:
x2
ρ=
4r
,
A=
π 2x 3
2r
,
V=
π x4
4r
(4.2.3.4.1)
54
El flujo de huecos (J) que se difunden del área del cuello al límite de grano (flujo en sentido inverso de
átomos por segundo y por cm 2 ), viene dado por la ley de Fick.
Ja =
DV dCV
Ω dx
(4.2.3.4.2)
donde:
DV = Coeficiente de difusión de las vacantes.
Ω = Volumen de un átomo o vacante.
dCV/dx = Gradiente de concentración de vacantes(En una dimensión).
CV = Fracción de lugares de red ocupados por vacantes
El incremento de la concentración de vcantes existente entre la superficie del cuello y la de la partícula,
∆CV, viene dado por:
γΩ
γ a3
∆CV = CV
= CV
kT ρ
kT ρ
(4.2.3.4.3)
3
siendo Ω = a el volumen atómico de la vacante que difunde.
Por otra parte, la variación de volumen del cuello (Volumen de materia transportada o de átomos que entran en
él) por unidad de tiempo será igual al flujo de átomos que penetran en el mismo (que será equivalente al flujo
de vacantes que abandonan el cuello), es decir,
dV
= J a Agb Ω
(4.2.3.4.4)
dt
donde:
Agb = Area de la sección transversal sobre la cual tiene lugar la difusión. La difusión en el límite de grano se
asume que ocurre sobre un espesor constante δgb, de tal modo que: Agb =2πXδgb donde X es el radio
del cuello.
Combinando las ecuaciones (4.2.3.4.2) y (4.2.3.4.4), y sustituyendo el valor de Agb, se obtiene:
dC
dV
= DV 2π X δ gb V
dt
dx
(4.2.3.4.5)
Puesto que el radio del cuello aumenta radialmente en dirección ortogonal a la línea que une los centros de las
esferas, la solución unidimensional es adecuada. Asumiendo que la concentración de vacantes entre la
superficie del cuello y el centro del cuello es constante, entonces:
dCV ∆CV
=
dx
X
donde ∆CV es la diferencia en la concentración de vacantes entre la superficie de cuello y el centro del cuello.
La concentración de vacantes en el centro del cuello se asume que es igual a la de una superficie plana libre de
tensiones CV0,. Se tiene que:
∆CV = CV − CV 0 =
CV 0γ SV Ω  1 1 
 + 
kT
 r1 r2 
(4.2.3.4.6)
donde:
r1, r2 = Radios de curvatura principales de la superficie del cuello.
55
Se tiene que:
r1 = r y r2 = - X
y se asume que X >> r, con lo que la ecuación (4.2.3.4.6) se transforma
en:
∆CV = CV − CV 0 =
CV 0γ SV Ω
kTr
(4.2.3.4.7)
Sustituyendo la ecuación (4.2.3.4.7) en la (4.2.3.4.5) resulta:
dV 2π DV CV 0δ gbγ SV Ω
=
dt
kTr
(4.2.3.4.8)
Usando las relaciones (4.2.3.4.1) que nos dan V y r y poniendo el coeficiente de difusión en el límite de
grano Dgb igual a DVCV0 se obtiene:
π X 3 dX
2a dt
=
2π Dgbδ gbγ SV Ω 4a
kT
X2
(4.2.3.4.9)
Simplificando, reordenando y separando variables resulta:
:
5
X dX =
16Dgbδ gbγ SV Ωa 2
kT
dt
(4.2.3.4.10)
integrando la expresión (4.2.3.2.10), se llega a la ecuación cinética (X = 0 para t = 0):
X
∫0
5
X dX =
16Dgbδ gbγ SV Ωa 2
kT
6
X =
t
∫0 dt
96Dgbδ gbγ SV Ωa 2
kT
t
(4.2.3.4.11)
o bien:
X  96Dgbδ gbγ SV Ω 
=

a 
kTa 4

1
6 1
t 6
(4.2.3.4.12)
La expresión (4.2.3.4.13) nos relaciona el diametro del cuello (X) de la superficie de contacto entre las partículas
(cuello) con las distintas variables que afectan al proceso. La importancia de la determinación de X radica en
que la resistencia mecánica, conductividad térmica y eléctrica y otras propiedades del sistema, están relacionadas
con el valor del parámetro X/a.
Para este mecanismo que densifica, puede determinarse la contracción lineal, definida como el cambio de
longitud ∆L dividido por la longitud inicial L0. A partir de la figura 4.2.1.1 una buena aproximación puede
escribirse del siguiente modo:
∆L
h
r
X2
=− =− =− 2
L0
a
a
4a
donde h es la mitad de la distancia de interpenetración entre las esferas.
56
Usando la ecuación (4.2.3.4.12) se obtiene:
 3Dgbδ gbγ SV Ω 
∆L
= −


L0
2kTa 4


1
3 1
t 3
(4.2.3.4.13)
Estos resultados indican que el crecimiento del cuello entre las partículas aumenta con 1/6 de la potencia del
tiempo (experimentalmente observado para muchos metales y sistemas cerámicos), y la contracción es
proporcional a los 1/3 de la potencia del tiempo. Representando graficamente (Figura 4.2.3.4.2) el valor de la
contraccion en funcion del tiempo, tomando como parametro la temperatura de sinterizacion, se deduce que esta
última es un parametro de primer orden que controla la cinetica de la sinterizacion. El tiempo sería un parametro
de segundo orden.
En la figura 4.2.3.4.3 se representan los datos experimentales para FNa y Al2O3.
Figura 4.2.3.4.2.- Leyes de contracción de un aglomerado para un mecanismo de sinterización por difusión.
Figura 4.2.3.4.3.-. Representación lineal (a) y doble logaritmica (b) de la contracción del fluoruro sódico y del
oxido de aluminio compactados.
De las ecuaciones obtenidas y de las otras ecuaciones que se obtendrían para las restantes formas de difusión
se concluye que el tiempo no es la variable más importante, ni la más critica, en el control de la sinterización.
57
El tamaño de partícula, por el contrario, ejerce un gran efecto en la velocidad de sinterización. En la figura
4.2.3.4.4 se representa el efecto de tamaño de partícula en el crecimiento del cuello para el Al2 O3
calentado a 1600°C, durante 100 horas. Se observa una dependencia muy marcada de la velocidad de
sinterización con el tamaño de partícula.
Figura 4.2.3.4.4.-. Efecto del tamaño de partícula sobre el crecimiento del área de contacto en Al2O3
calentada 100 horas a 1600°C.
De acuerdo con esto, partículas más finas pueden sinterizarse más rápidamente y a menor temperatura que agregados
de partículas más gruesas. Aunque no aparecen reflejadas en las ecuaciones (4.3.4.7 ) y (4.3.4.8), tienen gran
influencia en las propiedades finales del producto, la uniformidad del compacto (producto en verde, green-ware), la
forma de las partículas y su distribución por tamaños. Así, cuando el aglomerado poroso no tiene una
densidad uniforme, será muy difícil eliminar toda la porosidad durante la sinterización.
La forma de las partículas (Figura 4.2.3.4.5), también puede ser importante. La presencia de una concentración
demasiado elevada de partículas planas o alargadas, puede originar poros anchos o de geometría irregular
difíciles de eliminar.
58
Figura 4.2.3.4.5.- Forma de las partículas. a) Esferica; b) redondeada; c) angular; d) acicular; e) dendritica
f) irregular; g) porosa y h) fragmentada meca
La distribución por tamaños de las partículas puede ser crítica (Figura 4.2.3.4.6). Las partículas de un
mismo tamaño no se compactan convenientemente y retienen, con posterioridad a la sinterización, un
elevado porcentaje en volumen de porosidad. Resulta, pues, mas conveniente partir de mezclas de partículas con
diferentes granulometrías, lo que asegura, de partida, una mayor densidad del producto en verde.
Figura 4.2.3.4.6.- Modelos de disposición de las partículas en los aglomerados (a).- Disposicion cubica
simple. (b).-Disposición cúbica compacta. (c).-Disposicion cubica simple con partículas mas
pequeñas en los huecos intersticiales
La otra variable de gran importancia, que afecta a la velocidad del proceso, es el coeficiente de difusión, el cual
es altamente dependiente de la composición y de la temperatura.
La variación de los coeficientes de difusión con la temperatura obedece a una ley exponencial del tipo Arrhenius
(Figura 4.2.3.4.7):
−Q
kT
D = D0 D = D0e
(4.2.3.4.10)
El aumento de la temperatura aumentará el coeficiente de difusión y por tanto la velocidad de difusión y la
sinterización.
En las cerámicas iónicas deben considerarse los coeficientes de difusión del anión y del catión, En la alúmina
el oxígeno difunde rápidamente a lo largo de las fronteras de grano, mientras que el ión aluminio lo hace más
lentamente por lo que controla la velocidad global de la sinterización.
En general, la presencia de solutos aumenta los coeficientes de difusión y por tanto la velocidad de
sinterización. El coeficiente de difusión es proporcional a la concentración de huecos, la adición de impurezas
aumenta la contracción de huecos y por tanto el coeficiente de difusión.
59
Es necesario recalcar que las ecuaciones (4.2.3.4.8) y (4.2.3.4.9 ) anteriormente deducidas solo gobiernan el
proceso de sinterización en los estados iniciales , es decir, cuando los poros presentan una estructura continua y
abierta.
Figura 4.2.3.4.7.- Coeficientes de difusión de algunas materias primas cerámicas. La energía de activación Q
puede estimarse a partir de la pendiente y de la ordenada en el origen, para 0 en Ca0.14Zr0.3601,86
, Q = 29 Kcal/mol.
60
4.2.3.4.- Mecanismo de flujo viscoso.
En este mecanismo se asume que el transporte de materia esta gobernado por el concepto de balance de
energía de Frenkel:
(Velocidad de disipación de energía por flujo viscoso) =
= (Velocidad de energía ganada por reducción del área superficial)
Para los parámetros que se muestran en la figura 4.2.3.4.1 y asumiendo que el radio de la esfera permanece
prácticamente constante durante el flujo viscoso, la disminución del área superficial de las dos esferas viene
dada por:
S0 − S = 8π a 2 − 4π a 2 (1 + cos θ )
(4.2.3.4.1)
Hay que señalar que eso quiere decir que el material eliminado del plano de contacto se distribuye
uniformemente, en lugar de acumularse en el cuello. Para pequeños valores de θ, es decir para radios
pequeños del cuello, se tiene que:
cos θ ≈ 1 −
θ2
2
con lo que la ecuación (4.2.3.4.1) se transforma en:
S0 − S = 2π a 2θ 2
(4.2.3.4.2)
Figura 4.2.3.4.1.- Parámetros geométricos del modelo de dos esferas usado en la derivación de la ecuación de
la etapa inicial de la sinterización por flujo viscoso debida a Frenkel.
Por otra parte, la velocidad de cambio de energía debida a la reducción del área superficial puede escribirse
como:
•
E S = −γ SV
dS
d θ 2 
= 4π a 2γ SV  
dt
dt  2 
(4.2.3.4.3)
donde:
γSV = Energía específica superficial de la intercara sólido-vapor.
De acuerdo con Frenkel la velocidad de disipación de energía por flujo viscoso entre las dos esferas es:
•
EV =
16 3 • 2
πa ηu
3
(4.2.3.4.4)
donde:
61
η = Viscosidad de la fase vítrea.
1 d  aθ 2  d  θ 2 
u = Velocidad del movimiento para el flujo viscoso dada por: u =

=  
a dt  2  dt  2 
•
•
(4.2.3.4.5)
Esta ecuación se basa en la asunción de que el flujo ocurre uniformemente a lo largo de los ejes que unen los
centros de las esferas, en lugar de concentrarse en las proximidades del cuello.
Sustituyendo el valor de la velocidad del movimiento para el flujo viscoso dada por la expresión (4.2.3.4.5)
•
•
en la ecuación (4.2.3.4.4) y poniendo E S = E V se obtiene:
16 3 • d  θ 2 
d θ2 
π a η u   = 4π a 2γ SV  
3
dt  2 
dt  2 
(4.2.3.4.6)
Reordenando la ecuación (4.2.3.4.6) resulta:
•
3γ 
u =  SV 
4  ηa 
(4.2.3.4.7)
Sustituyendo el valor de la velocidad del movimiento para el flujo viscoso dada por la expresión (4.2.3.4.5) e
integrando con las condiciones iniciales θ = 0 para t = 0, se obtiene:
3γ 
θ 2 =  SV  t
2  ηa 
(4.2.3.4.8)
Puesto que θ = X/a, donde X es el radio del cuello, la ecuación (4.2.3.4.8) se transforma en:
X  3γ SV 
=
a  3η a 
1
2 1
t
2
(4.2.3.4.9)
4.2.3.5.- Resumen y limitaciones de las ecuaciones para la etapa inicial de la sinterización.
Las ecuaciones para el crecimiento del cuello y, para los mecanismos que densifican, de la contracción
pueden expresarse en la forma general:
m
H
X
  = nt
a
a
 ∆L 


 L0 
m
2
=−
(4.2.3.5.1)
H
t
2 a
m n
(4.2.3.5.2)
donde m y n son exponentes numéricos que dependen del mecanismo de sinterización y H es una función que
contiene los parámetros geométricos y de los materiales del sistema en polvo. Dependiendo de las asunciones
hechas en los modelos, se han obtenido un rango de valores para m, n y de la constante H. Los valores dados
en la tabla 4.2.3.5.1 representan los más plausibles para cada mecanismo.
62
La forma de las ecuaciones de crecimiento del cuello indican que una gráfica del log(X/a) en función del
log(t) es una línea recta con una pendiente igual a 1/m, entonces ajustando las predicciones teóricas a los
datos experimentales, puede encontrarse el valor del exponente m. Un procedimiento similar puede aplicarse
al análisis de la contracción si esta ocurre durante la sinterización. Los datos para validar los modelos
comúnmente se obtienen midiendo el crecimiento de cuello en sistemas simples (por ejemplo, dos esferas, una
esfera y un plato, o dos cables) ola contracción de una masa comprimida de partículas esféricas.
Ya que m es dependiente del mecanismo de sinterización, a primera vista puede parecer que la medida de m
proporcionaría información sobre el mecanismo de sinterización. Sin embargo, la asunción básica realizada en
los modelos de un solo mecanismo dominante para el transporte de masa no es válida en la mayoría de los
sistemas en polvo.
Tabla 4.2.3.5.1.- Valores de las constantes que aparecen en las ecuaciones para la etapa inicial de la
sinterización.
Cuando más de un mecanismo funciona simultáneamente, el exponente medido puede corresponder a un
mecanismo completamente diferente. Como ejemplo al considerar la sinterización inicial de polvos de cobre
Kingery y Berg mostraron que el crecimiento de cuello y los datos de contracción de esferas de cobre dieron
exponentes característicos de difusión de red como mecanismo dominante (Figura 4.2.3.5.1). Análisis
posteriores mostraron que la difusión superficial era el mecanismo dominante con una contribución
significativa de la difusión de red (que da lugar a la contracción). En el caso de la fase vítrea, el flujo viscoso
domina la sinterización, y la ecuación de crecimiento de cuello de Frenkel esta verificada por los datos de
Kuczynski.
También se deben recordar otras asunciones de simplificación de los modelos. La extensión de la geometría
de dos esferas a compactos de polvos reales es válida sólo si las partículas son esferas del mismo tamaño
dispuestas en un modelo uniforme. En la práctica, a ese sistema, a lo más, se acerca la consolidación uniforme
de polvos monodispersos por métodos coloidales. Coble consideró el efecto de una distribución de tamaño de
partícula sobre la etapa inicial de sinterización por considerando a una formación o disposición lineal de
esferas.
63
Figura 4.2.3.5.1.-Datos de la sinterización inicial de polvos de cobre: (a).-Crecimiento del cuello
(b).- Contracción. Los exponentes son característicos de la difusión de red como mecanismo
dominante
Johnson incluyó el ángulo diedral en su modelo de sinterización, pero la mayor parte de los modelos asumen
que la sección transversal de la superficie de cuello es circular, que es equivalente a la asunción de que el
ángulo diedral es de 180 ° o que la energía del límite de grano es cero. Simulaciones numéricas indican que la
asunción de que la sección transversal de cuello sea circular es extremamente simplificadora. Sin embargo,
los resultados de Johnson indican que despreciar la energía del límite de grano es insignificante si el ángulo
diedral es mayor de 150 °.
4.3.-Modelos para la etapa intermedia de la sinterización.
4.3.1.- Introducción.
La mayor parte de la densificación de un polvo compactado ocurre durante la etapa intermedia, que es la más
difícil de afrontar ya que depende fuertemente del tipo de empaquetamiento de las partículas, un parámetro
que es difícil evaluar. El modelo geometrico para esta etapa de los sistema policristalinos difiere del propuesto
para los sistemas amorfos.
64
4.3.2- Modelo geometrico para los sistemas policristalinos.
El modelo geométrico comúnmente usado para analizar la etapa intermedia de la sinterización ha sido
propuesto por Coble, el cual asume lo siguiente:
El polvo compactado se idealiza considerando que está compuesto de partículas en forma de
tetracaidecaedros, de igual dimensión, de longitud de arista ap, separados unos de los otros por canales de
poros longitudinales (cilíndricos) de radio rc, con el eje del cilindro coincidente con los lados del
tetracaidecaedro, cada uno de los cuales representa una partícula (Figura 4.3.2.1). Así, la celda unidad de la
estructura se toma como un tetracaidecaedro con poros cilíndricos a lo largo de sus bordes.
Un tetracaidecaedro se construye a partir de un octaedro trisectando cada vértice. La estructura pasa a tener
36 vértices, 24 aristas, y 14 caras (8 hexagonales y 6 cuadrado). El volumen del tetracaidecaedro es:
V = 8 2aP3
(4.3.2.1)
Cada poro es compartido por tres tetracaidecaedros, y si la r es el radio del poro, entonces el volumen total de
la porosidad por celda unidad es:
VP =
1
36π r 2aP )
(
3
(4.3.2.2)
El factor 1/3 se debe a que cada poro cilindrico esta compartido por tres tetracaidecaedros.
V
La porosidad de la celda unidad, P es, por lo tanto:
VT
3π  r 
PC =
 
2 2  aP 
2
(4.3.2.3)
Figura 4.3.2.1.- Modelo del tetracaidecaedro en la etapa intermedia de la sinterización.
La red de poros cilíndricos localizados sobre los bordes de granos en forma de
tetracaidecaedros esta altamente interconectada.
65
4.3.3.- Mecanismos.
Ya que el modelo asume que la geometría de los poros es uniforme, los mecanismos que no producen
densificación no pueden operar. Esto es debido a que el potencial químico es el mismo en todas las partes
sobre la superficie de poro. Por tanto, solo operan los mecanismos que dan lugar a densificación: difusión de
red y difusión por límite de grano. No se espera que el flujo plástico funcione de modo significativo para
sistemas cerámicos.
La densificación tiene lugar por difusión volumétrica de vacantes alejándose de los canales de poros
cilíndricos hacia los bordes de grano (flechas curvadas en la figura 4.3.3.1).
Figura 4.3.3.1.- Vista expandida de uno de los canales de poros cilíndricos. Las vacantes pueden difundir bajo
los bordes de grano (flecha con trazos) o a través del volumen (flechas sólidas). Hay que
señalar que en ambos casos las vacantes son aniquiladas en los bordes de grano.
Se establece un perfil lineal constante de la concentración de vacantes entre la fuente y el sumidero. Las
vacantes son eliminadas en los bordes de grano, es decir, los bordes de grano actúan como sumidero de
vacantes. Se asume también que donde las vacantes son eliminadas, su concentración está dada por C0, es
decir, bajo una interfase planar libre de tensiones.
4.3.4.- Ecuaciones de la sinterización.
Siguiendo el análisis de Coble, se derivarán las ecuaciones cinéticas de la sinterización por difusión en red y
difusión en borde de grano.
4.3.4.1.- Difusión en red o volumétrica.
La figura 4.3.4.1.1.a muestra que los poros cilíndricos a lo largo de los bordes de grano encierran cada cara
del tetracaidecaedro. Como el flujo de vacantes de los poros termina sobre las caras divisorias (figura
4.3.4.1.1.b), Coble asumió la existencia de difusión radial desde una fuente circular de vacantes y desprecio
los efectos de forma en los vértices del tetracaidecaedro. Para que el borde permanezca plano, el flujo de
vacantes por unidad de área del borde debe ser el mismo sobre el borde total.
66
El flujo por unidad de longitud del cilindro viene dado por:
J
= 4π DV ∆C
L
(4.3.4.1.1)
donde DV es el coeficiente de difusión de vacantes y ∆C es la diferencia en la concentración de vacantea entre
el poro (fuente) y el borde de grano (sumidero).
Asumiendo que:
1.- La convergencia del flujo hacia el límite no cambia cualitativamente la ecuación del flujo con respecto a su
dependencia del radio del poro
2.- La anchura del campo de flujo, L, es decir la equivalencia de L en la ecuación (4.3.4.1.1), es igual al
diámetro de poro.
3.- El flujo se aumenta en un factor de 2, debido a la libertad del flujo de difusión de vacantes para divergir al
principio, proporcionando un área adicional disponible.
Con dichas asunciones la ecuación (4.3.4.1.1) se transforma en:
J = 2(4π DV ∆C )2r
(4.3.4.1.2)
Figura 4.3.4.1.1.- (a).- Las ecuaciones de la etapa intermedia de la sinterización para sólidos policristalinos
están basadas en un cuello hexagonal (b).- la sección (sobre A-A) muestra un corte a través del
cuello con los caminos de flujo atómicos para el borde de grano y la difusión de red.
Puesto que hay 14 caras en un tetracaidecaedro y cada cara esta compartida por 2 granos, el flujo de volumen
por celda de unidad es:
dV 14
= J = 112π DV ∆Cr
dt
2
(4.3.4.1.3)
Para el poro cilíndrico en la etapa intermedia de la sinterización , los dos radios de curvatura principales son r
e infinito ( ∞ ) , con lo que ∆C viene dada por:
∆C =
CV 0γ SV Va
kTr
(4.3.4.1.4)
67
Sustituyendo el valor de ∆C en la ecuación (4.3.4.1.3) y poniendo DL = DV CV 0 , donde DL es el coeficiente
de difusión de red, resulta:
dV =
112π DLγ SV Va
kT
dt
(4.3.4.1.5)
La integral de dV es igual al volumen de la porosidad dada por la ecuación (4.3.2.2), es decir:
2
∫ dV =12π r ap 
r
(4.3.4.1.6)
r0
y combinado lo anterior con la ecuación (4.3.4.1.5) da:
t
DLγ SV Va  f
2
≈ −10
r
t
r
a p kT 
t
0
(4.3.4.1.7)
donde t f es el tiempo transcurrido hasta que el poro desaparece. Dividiendo ambos lados de la ecuación
(4.3.4.1.7) por ap2 e integrando
PC ≈
r2
a p2
≈ 10
DLγ SV Va
a p3 kT
( tf − t )
(4.3.4.1.8)
expresión que nos da la fracción de porosidad, Pc, en la etapa intermedia de la sinterización la cual decrece
linealmente,
En vista de las aproximaciones usadas por Coble, esta ecuación sólo puede ser considerada como un cálculo
de un orden de magnitud. Este modelo se aplica hasta que los poros se hacen aislados.
Las ecuaciones de sinterización, comúnmente, se expresan en términos de la velocidad de densificación.
Usando la relación entre porosidad P y densidad relativa ρ, es decir , P = 1- ρ, y diferenciando la ecuación
(4.3.4.1.8) con respecto al tiempo, se obtiene:
Dγ V
d
dρ
(PC ) = −
≈ −10 L 3SV a
dt
dt
a p kT
(4.3.4.1.9)
Tomando ap como, aproximadamente, igual al tamaño de grano G, y escribiendo la velocidad de
densificación en forma de una velocidad de deformación volumétrica , la ecuación (4.3.4.1.9) se transforma
en:
D γ Va
1 dρ
≈ 10 L SV
ρ dt
ρG 3 kT
(4.3.4.110)
Esta ecuación predice que la velocidad de densificación a una densidad fija es inversamente proporcional al
cubo del tamaño de grano.
68
4.3.4.2.- Difusión en borde de grano.
Usando el mismo modelo geométrico descrito para la difusión de red y modificando las ecuaciones de flujo
para tener en cuenta la difusión de borde de grano, Coble derivo la ecuación siguiente:


r 2  DBGδ BG γ SV Va  2 3
PC = 2 =
t
a p  ρ (1 − ρ ) 12 G 4 kT 


(4.3.4.2.1)


1 d ρ 4  DBGδ BG γ SV Va 
=
ρ dt 3  ρ (1 − ρ ) 12 G 4 kT 


(4.3.4.2.2)
que puede ponerse en la forma:
Esta ecuación predice que la velocidad de densificación a una densidad fija es inversamente proporcional a
la cuarta potencia del tamaño de grano.
Lo que es interesante en este proceso es que se autoacelera, desde que los cilindros se hacen más pequeños en
diámetro, su curvatura se incrementa y el gradiente de concentración de vacantes también se incrementa. Este
proceso no sigue indefinidamente; a medida que los poros se hacen más largos y más finos, en ese punto se
hacen inestables (inestabilidad de Rayleigh) y se dividen en poros esféricos más pequeños a lo largo de los
bordes de grano y/o en los puntos triples entre los granos. Es en dicho instante, en que la etapa intermedia de
la sinterización finaliza y comienza la etapa final.
Mientras que el canal de poros puede contraer por difusión superficial, la longitud del camino para el
transporte es muy grande y entonces la contracción es controlada por difusión volumétrica o difusión en borde
de grano.
4.3.3- Modelo geometrico para los sistemas amorfos.
Scherer ha propuesto la estructura mostrada en la figura 4.3.3.1 como un modelo para la etapa intermedia de
la sinterización de materiales amorfos. Consiste en una disposición cúbica formada por cilindros que se
cruzan y la densificación se asume que se lleva a cabo ya que los cilindros van haciéndose más cortos y de
mayor espesor. El modelo puede verse como una estructura idealizada en la cual los cilindros representan las
cuerdas de partículas esféricas unidas por cuellos.
La estructura esta representada por una celda unidad que consiste en 12 cuartas partes del cilindro (Figura
4.3.3.1.a). El volumen de la fase sólida en la celda unidad es:
VS = 3π a 2 L − 8 2a 3
(4.3.3.1)
donde la L es la longitud del lado de la celda unidad y a es el radio del cilindro. Ya que el volumen total de la
3
célula es L , la densidad de la celdad, d, es igual a:
d V
d = S 3S
L
donde dS es la densidad teórica de la fase sólida. La densidad relativa ρ, definido como d/dS, esta dada por:
ρ = 3π x 2 − 8 2 x3
(4.3.3.2)
donde: x = a/L. De acuerdo con esa ecuación ρ es una función solamente de a/L.
69
Figura 4.3.3.1.- Modelo de Scherer para la sinterización viscosa.
(a).- Celda unidad de la estructura con una longitud del lado L y radio del cilindro a.
(b).- Microestructura con una densidad relativa de ∼0.1
(c).- Microestructura con una densidad relativa de ∼0.5
La inversa de la ecuación (4.3.3.2) es:
x=
π 2 1
4π  

+ cos  Θ +


8 2
3  

(4.3.3.3)
donde:
  4 3 
1
Θ = arc cos 1 −   ρ 
3
  π  
(4.3.3.4)
3
El volumen de fase sólida en la celda unidad es ρl . Este volumen no cambia y también puede ponerse igual
3
a ρ0l0 , donde ρ0 y l0 son los valores iniciales de la densidad relativa y de la longitud, respectivamente, de la
celda unidad. Cada celda contiene un poro, por lo que el número de poros por unidad de volumen de la fase
sólida es:
1
N=
(4.3.3.5)
ρ0l03
El modelo debería de ser válido hasta que los cilindros adyacentes se toquen, aislando de este modo los poros.
Esto ocurre cuando (a/L) = 0.5, es decir cuando ρ = 0.94.
70
La derivación de las ecuaciones de la sinterización basándose en el modelo de Scherer es bastante similar a la
utilizada por Frenkel para la derivación de las ecuaciones de la sinterización de la etapa inicial. El resultado
es:
γ SV N
∫t0 η
t
1
3
dt = ∫
2dx
x
x0
(3π − 8 2 x )
1
3
x
2
(4.3.3.6)
3
donde:
γSV = Energía específica de superficie de la intercara sólido-vapor.
η = Viscosidad de la fase sólida.
La integral del segundo miembro de la ecuación (4.3.3.6) puede determinarse haciendo el cambio variables:
 3π

y =
−8 2 
 x

1
3
(4.3.3.7)
El resultado puede escribirse como:
γ SV N
η
1
3
( t − t0 ) = FS ( y) − FS ( y0 )
(4.3.3.8)
donde:
2  1  α 2 − α y + y2 
 2 y − α 



+ 3 arctan 
FS ( y ) = −
Ln

α  2  (α + y ) 2 
α
3

 



(
α= 8 2
1
)3
(4.3.3.9)
Las predicciones del modelo se expresan normalmente en términos de una curva de ρ en función de
γ SV N
η
1
3
( t − t0 ) , denominado como tiempo reducido.
La curva se obtiene así: Para un valor dado de ρ el parámetro y se obtiene de las ecuaciones (4.3.3.3) y
(4.3.3.7). Entonces la función FS(y) se determina a partir de la ecuacion (4.3.3.9) y el tiempo reducido de la
ecuación. (4.3.3.8). El procedimiento se repite para otros valores de ρ. Las predicciones del modelo se
muestran en la curva de la figura 4.3.3.2. La curva tiene la forma sigmoidal característica que se observa para
la variación de los datos de la densidad en función del tiempo en muchos experimentos de sinterización. El
modelo ha sido ampliado considerando una distribución de tamaños de poro gaussiana o bimodal.
Las predicciones del modelo de Scherer han sido validadas por los datos de muchos materiales amorfos como
geles coloidales, geles poliméricos y partículas vítreas consolidadas. En comparación con los datos
experimentales, las predicciones del modelo se dibujan en función del tiempo reducido, mientras que los datos
se obtienen en función de tiempo medido (por ejemplo, segundos). Para construir tal gráfica, primero hay que
encontrar el tiempo reducido correspondiente a la densidad medida como se ha descrito anteriormente. Una
gráfica del tiempo reducido en función del tiempo medido debería ser una línea recta con una pendiente igual
γ N
a SV
η
1
3
.
Multiplicando la pendiente por el tiempo medido se obtiene el intervalo de tiempo reducido promedio para
cada densidad. Los puntos de la figura 4.3.3.2 muestran una comparación de los resultados de la sinterización
de cuerpos de densidad baja formados del hollín SiO2 con las predicciones del modelo de Scherer.
71
4.4.- Modelo de sinterización de sistemas policristalinos en la etapa final. Eliminación de poros.
4.4.1.- Introducción.
En la etapa final de la sinterización tiene lugar la desaparición de la porosidad que aún permanece y el
crecimiento de grano. Cuando los átomos difunden hacia los poros y las vacantes son transportadas lejos de
los poros hacia un sumidero tal como bordes de grano, dislocaciones o superficies externas del cristal, los
poros podrán ser eliminados.
En la etapa final de la sinterización de materiales policristalinos, el sistema es idealizado en términos de una
serie de tetracaidecaedros de igual tamaño con poros esféricos del mismo tamaño en vértices (Figura 4.4.1.1).
El tetracaidecaedro tiene 24 poros (uno en cada vértice) y cada poro esta compartido por cuatro
tetracaidecaedros, por lo que el volumen de poro asociado a cada tetracaidecaedro es:
VP =
24 4 3
πr
4 3
donde la r es el radio de un poro. Haciendo uso de la ecuación
VT = 8 2a p3
la porosidad del tetracaidecaedro simple es:
8π r 3
π  r
PS =
=

8 2a p3
2  a p



3
(4.4.1.1)
Figura 4.4.1.1.- Esquema de la etapa final de la sinterización. Los poros son inclusiones tetraédricas
en los vértices donde se encuentran cuatro tetracaidecaedros.
Una celda unidad más conveniente de la estructura idealizada puede ser representada por una corona esferica
de gran espesor de material sólido centrada en un poro de radio r (Figura 4.4.1.2). El radio exterior de la
corona esférica se define de tal modo que la densidad media de la celda unidad sea igual a la densidad del
sistema en polvo, esto es:
r 
ρ = 1−  
b
3
(4.4.1.2)
72
Figura 4.4.1.2.- Sólido poroso durante la etapa final de la sinterización puede modelarse construyendo una
corona esférica centrada en un poro.
El volumen de la fase sólida en la celda unidad es :
(
4
π b3 − r 3
3
)
Puesto que una celda unidad contiene un solo poro , el número de poros por unidad de volumen de la fase
sólida es:
N=
3  1− ρ 


4π  ρ r 3 
(4.4.1.3)
4.4.2.- Ecuaciones de la etapa final de la sinterización.
4.4.2.1.- Introducción.
En la etapa final de la sinterización, como en la etapa intermedia, la asunción de la geometría de poro
uniforme en los modelos excluye la presencia de los mecanismos que no producen densificación.
4.4.2.2.- Modelo basado en la difusión volumétrica.
En este modelo, la fuente de vacantes es la superficie de los poros de radio ρP y el sumidero es la superficie
esférica de radio R, donde R >> ρP (Figura 4.4.2.2.1).
73
Figura 4.4.2.2.1.- Construcción geométrica usadas para modelizar la eliminación de la porosidad, por
difusión volumétrica, donde se asume que las vacantes son eliminadas en la superficie de
los granos.
Dada la simetría esférica del problema, se demuestra que:
cVAC = B +
A
r
(4.5.2.2.1)
es una solución a la primera ley de Fick cuando esta última se expresa en coordenadas esféricas, y cVAC es la
concentración de vacantes en cualquier localización. Asumiendo que se aplican las siguientes condiciones de
borde (Figura 4.4.2.2.1):
- en r = ρP ,
- en r = R ,
cVAC = CCURV
cVAC = C0
puede demostrarse que:
1
R
 dcVAC 
= − ∆CVAC
 dr 
ρP
R − ρP

 r = ρP
(4.4.2.2.2)
satisface las condiciones de borde y estado estacionario, y ∆CVAC está dado por la ecuación:
∆CVAC = CCURV − C0 = −C0
κγ SV Ω
kT
Por tanto, el flujo total de vacantes moviéndose radialmente lejos del poro es:
 dc

R
JS = −4πρP2 DV  VAC 
= 4πρP ∆CVAC
R − ρP
 dr r = ρP
(4.4.2.2.3)
donde S es el área superficial del poro. El volumen total eliminado por unidad de tiempo es pues:
74
8πγ SV Ω R
dV
= −JaSV = −Da
dt
kT R − ρP
(4.4.2.2.4)
donde el producto DvΩC0 es reemplazado por la difusividad del ión limitante de la velocidad Da en el
volumen. Para un poro esférico:
dV = 4πρP2 d ρP
que se sustituye en la ecuación (4.4.2.2.4), con lo que separando variables:
ρP2 d ρP = −Da
2γ SV Ω
kT
R
dt
R − ρP
(4.4.2.2.5)
dt
(4.4.2.2.5)
y como R >> ρP
ρP2 d ρP = −Da
2γ SV Ω
kT
e integrando se obtiene la solución final, es decir:
ρP3 − ρP3 ,0 = −
6Da γ SV V
kT
t
(4.4.2.2.7)
donde ρP,0 es el tamaño inicial de los poros en el tiempo t = 0. Para relacionar el radio del poro con la
porosidad Pc, se usa nuevamente el modelo presentado en la figura 4.3.2.1. Se asume que está presente un
poro en los vértices de cada tetracaidecaedro; y como hay 24 vértices y cada poro es compartido por 4
poliedros, se sigue que la fracción de porosidad está dado por:
Pc =
8πρ 3p
8 2a 3p
=
πρ 3p
(4.4.2.2.8)
2a 3p
donde el denominador representa el volumen del tetracaidecaedro. Combinando este resultado con la ecuación
(4.4.2.2.7), y destacando que el tamaño de grano d aumenta con ap se tiene:
Pc − P0 = −(Cons tan te)
Dambiγ SV Ω
d 3kT
t
(4.4.2.2.9)
donde P0 es la porosidad al comienzo del estado final de sinterización. Este modelo predice que la porosidad
3
durante este estado decrecerá linealmente con el tiempo e inversamente con d . En otras palabras, granos más
pequeños deben provocar una mucha más rápida eliminación de la porosidad, lo que se esperaba desde que se
asumió que los bordes de grano actuaban como sumideros.
4.4.2.3.- Modelo basado en la difusión en borde de grano.
La ecuación (4.4.2.2.9) tiene validez limitada, sin embargo, debido a que como se comenta con más detalle
abajo, la eliminación de los últimos remanentes de vacancias ocurre solamente si ellos permanecen adjuntos a
los bordes de grano, donde son eliminados. La geometría apropiada es presentada esquemáticamente en la
75
figura 4.4.2.3.1, y siguiendo una derivación similar a la llevada a cabo en el Apéndice I-D, se puede demostrar
que:
4
ρ p4 - ρp,0
=
-8δ bg Dbgγ SV Ω
kT
1
t
 Rbg

log 
ρ p 

(4.4.2.3.1)
donde Rbg es definido en la figura 4.4.2.3.1. En otras palabras, si la difusión en borde de grano es el
1/4
mecanismo operativo, el tamaño promedio de poro debe contraer con t más que con la dependencia t1/3
esperada si la difusión volumétrica fuera importante (Ecuación (4.4.2.2.7)).
Figura 4.4.2.3.1.- Construcciones geométricas usadas para modelar la eliminación de la porosidad, asumiendo
difusión en borde de grano, donde las vacantes están limitadas a difundirse a lo largo de un
borde de grano de ancho δbg.
La importancia de la microestructura se ilustra en la figura 4.4.2.3.2. Para una muestra con un mayor número
de poros, todos del mismo tamaño, sobre un límite de grano la distancia media de difusión es más pequeña
cuando hay más poros, y su eliminación se logra más rápidamente para la muestra con la porosidad más alta.
Así, aunque las condiciones que influyen en la velocidad de volumen de sinterización - coeficiente de difusión
de volumen o de limite de grano (y por lo tanto, la temperatura y la concentración de soluto), la energía
superficial y el tamaño de poro – están bien establecidas, la relación geométrica existente entre las fronteras
de grano y los poros puede tener una gran variedad de formas y es crítica en la determinación de lo que ocurre
en realidad.
Figura 4.4.2.3.2.- La distancia media de difusión para el transporte de material es más pequeña cuando hay
más de un poro del mismo tamaño en el limite de grano.
76
Con materiales de grano fino como los óxidos, es habitual observar un aumento tanto del tamaño de grano
como del tamaño de poro durante las primeras etapas del tratamiento térmico, como se ilustra en las figuras
4.4.2.3.3 y 4.4.2.3.4 para la alumina Lucalox. Esto, parcialmente, es el resultado de la presencia de
aglomerados de partículas finas que sinterizan rápidamente, dejando poros entre ellos y en parte es debido al
rápido crecimiento de grano durante el cual los poros son aglomerados moviéndose con las fronteras de grano,
como se ilustra en la figura 4.4.2.3.5. En los casos en los cuales la sinterización de las partículas finas en
grupos es significativa , la molienda para romper los aglomerados conduce a un aumento notable de la
velocidad de sinterización.
Figura 4.4.2.3.3.- Desarrollo progresivo de la microestructura en la alúmina Lucalox, (a).- Partículas iniciales
en el compacto (x5000), (b).- Después de 1 minuto a 1700 ºC (x5000), (c).- Después de 2.5
minutos a 1700 ºC (x5000), (d).- Después de 6 minutos a 1700 ºC (x5000). Puede observarse que
los granos y los poros aumentan de tamaño, que hay variaciones en el empaquetamiento y en el
tamaño poro y que los poros permanecen localizados entre los granos densos. (e).Microestructura final casi libre de poros, con solamente unos pocos poros localizados dentro de
los granos (x500).
77
Figura 4.4.2.3.4.- Crecimiento de grano y de poro en una muestra de UO2 después de: (a).- 2 minutos a 1600
ºC, 91.5 % denso (x400), (b).- Después de 5 horas a 1600 ºC, 91.9 % denso (x400).
Figura 4.4.2.3.5.- (a).- Distorsión de la forma esférica del poro por movimiento de la frontera de grano
(b).- Aglomeración de los poros durante el crecimiento de grano
78
Pequeñas variaciones en el empaquetamiento inicial de las partículas se exageran durante el proceso de
crecimiento de poro. Además, los espacios entre aglomerados y los huecos ocasionales más grandes resultan
de la unión entre las partículas o aglomerados presentes (Figura 4.4.2.3.6). Por consiguiente, durante la etapa
intermedia del proceso de sinterización hay un rango de tamaños de los poros presentes, y la eliminación
lenta de los poros más grandes conduce a variaciones en la concentración de poro en las etapas posteriores del
proceso de sinterización, como se ilustra en la figura 10 4.4.2.3.7.c.
Figura 4.4.2.3.6.- Huecos grandes formados por unión de aglomerados en un polvo fino de Al2O3 (x2000).
Figura 4.4.2.3.7.- Variaciones de concentración de poros resultado de: (a).- Variación en el tamaño de los
granos (b).- Fricción en el molde (c).- Diferencias en el empaquetamiento local y en la
aglomeración (d).- Eliminación más rápida de los poros en la proximidad de la superficie.
79
Además de la presencia aglomerados y de diferencias en el empaquetamiento, las variaciones de
concentración de poros en las últimas etapas de la sinterización pueden ser el resultado de variaciones en el
tamaño de partícula en el polvo de partida, de variaciones de la densidad de la pieza en verde causadas por la
fricción en las paredes del molde durante el prensado y de la eliminación más rápida de la porosidad cerca de
la superficie causada por gradientes de temperaturas durante el calentamiento, como se muestra en la figura
4.4.2.3.7.
La importancia de las variaciones locales en la concentración de poros resulta del hecho de que la parte de la
muestra que contiene poros tiende a contraerse, pero es frenada por las partes libres de poros. La distancia de
difusión eficaz ya no es mayor del poro a un límite de grano adyacente, sino que la distancia de poro a poro o
de superficie a poro es varios órdenes de magnitud más grande. Un ejemplo de un racimo de poros residuales
en un óxido sinterizado se muestra en la figura 4.4.2.3.8.
Figura 4.4.2.3.8.- Racimo de poros residuales en una muestra 90 % molar de Y2O3 - 10 % molar de ThO2
resultado de un procesado inadecuado del polvo.
No sólo la cinética de eliminación de poros puede conducir a una porosidad "estable" y residual, sino que es
también posible, en algunos casos, tener un equilibrio termodinamicamente metaestable de la configuración
de los poros. En la figura 4.4.2.3.2 se han representado poros esféricos localizados sobre un límite de grano, el
modelo de descripción habitual nos dice que hay un ángulo diedral Φ, en la intersección poro-límite de grano
determinado por las energías de intercara relativas:
 Φ  γ gb
cos   =
 2  2γ SV
80
En la mayor parte de los casos el ángulo diedral para los óxidos puros es aproximadamente 150º y la
aproximación de la forma esférica para los poros es buena. Para la composición Al2O3 + 0.1 % MgO el valor
es 130°, para el UO2 + 30 ppm C el valor es de 88 ° y para el carburo de boro impuro el valor es
aproximadamente 60 °. Para estos materiales las consecuencias de poros no esféricos tienen que ser
consideradas.
En el crecimiento discontinuo de grano y como se ilustra en las figuras 4.4.2.3.9 y 4.4.2.310, la curvatura
divisoria entre granos o fases depende tanto del valor del ángulo diedral como del número de granos
circundantes.
Figura 4.4.2.3.9.- Representación esquemática de una muestra policristalina. El signo de la curvatura de las
fronteras de grano cambia cuando el número de lados aumenta desde menos de 6 a más de
6, y el radio de curvatura es menor. La mayoría del número de lados difiere de 6. Las
flechas indican las direcciones en las cuales migran las fronteras de grano.
Figura 4.4.2.3.10.- Crecimiento de un cristal grande de Al2O3 en una matriz de granos de tamaño uniforme
(x495). Comparase con la figura 4.4.2.3.9.
81
Si se toma como r el radio de una esfera circunscrita alrededor de un poro poliédrico rodeado por granos, la
relación del radio de curvatura de las superficies del poro ρ al radio esférico depende tanto del ángulo diedral
como sobre el número de granos circundantes, como se muestra en la figura 4.4.2.3.11.a. Cuando la relación
(r/ρ) disminuye hasta cero, las intercaras son planas y no tienen ninguna tendencia a la contracción. . Cuando
(r/ρ) es negativa, el poro tiende a crecer, como se ilustra en la figura 4.4.2.3.11.b.
Figura 4.4.2.3.11.- (a).- Cambio en la relación (r/ρ) con el ángulo diedral para poros rodeados por diferente
número de granos como se indica en las curvas individuales, (b).- Condiciones para la
estabilidad del poro.
82
Para un tamaño de grano uniforme la forma del espacio lleno es un tetracaidecaedro con 14 granos
circundantes. A partir de una relación aproximada entre el número de granos circundantes y de la relación
entre el diámetro de poro y el diámetro de grano se puede derivar una relación para la estabilidad de los poros
en función del angulo diedral y de la relación (Tamaño poro/Tamaño grano) como se muestra en la figura
4.4.2.3.12. De esta figura puede verse que los grandes poros presentes en polvos pobremente compactados,
tales como se muestra en la figura 4.4.2.3.6, no solo permanecen estables sino que crecen.
Figura 4.4.2.3.12.- Condiciones para la estabilidad del poro.
Se ha comprobado que para la estabilidad de los poros no es necesario que exista una gran disparidad entre el
tamaño de poro y el de grano. El lugar y tamaño de la porosidad relativa con respecto a la red grano-límite, no
solamente afecta a la distancia necesaria para la difusión, sino también a la fuerza motriz para el proceso.
4.5.- Modelo geometrico de sinterización de sistemas amorfos en la etapa final.
Un modelo que consiste en la cáscara esférica mostrada en la figura 4.4.1.2 pero sin las fronteras de grano ha
sido usado por Mackenzie y Shuttleworth para deducir las ecuaciones de la etapa final de la sinterización por
flujo viscoso de un sólido amorfo. El empleo del modelo significa que el verdadero sistema es idealizado en
términos de una estructura que consiste en los poros esféricos del mismo tamaño en una matriz sólida. La
cáscara concéntrica mantiene su geometría esférica durante la sinterización. A diferencia de la etapa inicial,
ecuaciones exactas pueden ser sacadas en el concepto de equilibrio de energía de Frenkel para la velocidad de
reducción de área de la superficie y la velocidad de disipación de energía por el flujo viscoso. El resultado es:
γ N
∫t0 SVη
t
1
3
2 3 
dt = 

3  4π 
1
3
ρ
∫ρ0
dρ
(1 − ρ )
2
3
ρ
1
3
(4.5.1)
donde:
ρ = Densidad relativa en el instante t.
ρ0 = Densidad relativa en el instante inicial, t = t0.
γSV = Energía específica de superficie de la intercara sólido-vapor.
η = Viscosidad de la fase sólida.
N = Número de poros por unidad de volumen (Ecuación (4.4.1.3))
83
La ecuación (4.5.1) puede escribirse en la forma:
γ SV N
η
1
3
( t − t0 ) = FMS ( ρ ) − FMS ( ρ0 )
(4.5.2)
donde:
2 3 
FMS ( ρ ) = 

3  4π 
1
3
 1  1+ ρ3 
 2ρ −1 
 Ln 

− 3arctg 

 2  (1 + ρ )3 
3 



(4.5.3)
La forma de la ecuación (4.5.2) es similar a la del modelo de Scherer para la etapa intermedia [Ecuación
(4.3.3.8)] y las predicciones para la cinética de sinterización pueden analizarse de una manera similar a la
señalada para el modelo de Scherer.
Una comparación de las predicciones del modelo de Mackenzie y Shuttleworth con el modelo de Scherer se
muestra en la figura 4.5.1. A pesar de la diferencia en la geometría de los modelos, la concordancia es
excelente sobre una amplia gama de densidad. Se presentan desviaciones significativas sólo cuando ρ cae
debajo de ∼0.2. Aunque el modelo de Mackenzie y Shuttleworth es estrictamente válido para ρ mayor que
∼0.9, las predicciones son aplicables sobre un rango mucho más amplio. Una situación similar existe para el
modelo de Scherer. Las predicciones muestran una concordancia excelente no sólo con el modelo de
Mackenzie y Shuttleworth, sino también con el modelo de Frenkel para la etapa inicial. La conclusión que se
puede sacar es que a diferencia del caso de los materiales policristalinos, el comportamiento durante
sinterización de los materiales amorfos no es sensible a los detalles estructurales.
Figura 4.5.1.- Densidad relativa en función del tiempo reducido para el modelo de Mackenzie y Shuttleworth
y el modelo de Scherer. Para densidades relativas mayores de 0.942, se aplica el modelo de
Mackenzie y Shuttleworth. Las curvas han sido ajustadas para coincidir en el tiempo tf cuando
la sinterización es completa.
4.6.- Factores que afectan al proceso de sinterización.
Los factores más importantes que controlan el proceso de sinterización se enumeran a continuación:
1.- Densidad en verde.
Existe una correlación entre la densidad en verde (previa a la sinterización) y la densidad final, dado que con
una densidad en verde más alta, tiene que eliminarse un menor volumen de poros.
84
2.- Uniformidad de la microestructura en verde.
Más importante que la densidad en verde es la uniformidad de la microestructura en verde y la ausencia de
aglomerados.
3.- Distribución de tamaño.
Distribuciones de tamaño de grano estrechas disminuirán
anormal.
la tendencia hacia un crecimiento de grano
4.- Temperatura.
Puesto que la difusión es la responsable de la sinterización, claramente el incremento de la temperatura
mejorará la cinética de sinterización, debido a que el coeficiente de difusión D es activado térmicamente.
Como se destacó anteriormente, las energías de activación para la difusión volumétrica son usualmente más
altas que aquellas para las difusiones en borde de grano y superficiales. Por lo tanto, el aumento de la
temperatura mejora los mecanismos de difusión volumétrica que son los que conducen a la densificación.
5.- Atmósfera de sinterización.
El efecto de la atmósfera puede ser crítico en la densificación de un polvo compactado. En algunos casos, la
atmósfera puede mejorar la difusividad de especies controlantes de la velocidad, por ejemplo, por influencia
en la estructura de los defectos. En otros casos, la presencia de un cierto gas puede promover el aumento del
tamaño de grano por la mejora de la presión de vapor y la supresión total de densificación.
Otra importante consideración es la solubilidad del gas en el sólido. Gases con limitada solubilidad pueden
provocar una porosidad residual. De este modo, debido a que la presión del gas dentro de los poros se
incrementa a medida que ellos se contraen, es importante elegir un gas de atmósfera de sinterización que se
disuelva fácilmente en el sólido.
6.- Impurezas.
El papel de las impurezas
comentados como sigue:
ha sido extensamente estudiado, y hasta la fecha sus efectos pueden ser
(a).- Aditivos de sinterización. Se añaden intencionadamente para formar una fase líquida. También es
importante señalar que el papel de las impurezas no siempre se aprecia. La presencia de impurezas puede
formar eutécticos de baja temperatura con lo que la cinética de los procesos de sinterización puede mejorarse,
aún en muy pequeñas concentraciones.
(b).- La supresión del aumento del tamaño de grano por reducción de la velocidad de evaporación y el
descenso de la difusión superficial. Un ejemplo clásico son las adiciones de boro al SiC, sin las que el SiC no
podría densificar.
(c).- La supresión del crecimiento de grano y la disminución de la movilidad del borde de grano.
(d).- Mejora de la velocidad de difusión. Una vez que se identifica el ión limitante de la velocidad durante la
sinterización, la adición del dopante apropiado, que entraría en solución y crearía vacantes en la subred,
debería, en principio, mejorar la cinética de densificación.
7.- Tamaño de partícula.
Dado que la fuerza motriz para la densificación es la reducción del área superficial, mientras más grande es el
área superficial inicial más grande es la fuerza motriz, parecería que se debería usar el tamaño de partícula
85
más fino posible. Aunque en principio esto parece una buena decisión, en la práctica partículas muy finas
presentan serios problemas. A medida que la relación (Superficie/Volumen) de las partículas se incrementa las
fuerzas electrostáticas y otras fuerzas superficiales se convierten en dominantes, lo que lleva a la
aglomeración de las partículas. Cuando se produce el calentamiento, los aglomerados tienden a sinterizar
junto a las partículas más grandes, lo que no solamente elimina la fuerza motriz para la densificación sino que
también crea grandes poros entre los aglomerados parcialmente sinterizados que posteriormente son difíciles
de eliminar.
Se destaca que la dependencia del tamaño de partícula se debe al incremento en la fuerza motriz (a través de
cambios de curvatura) y en la cinética (a través de cambios en la longitud del camino). Asumiendo que uno de
los mecanismos es dominante y que el grado de sinterización está dado por la relación del tamaño del cuello,
x, a el tamaño de partícula, r, el tiempo de sinterización para lograr la misma densidad por dos tamaños de
partículas, r1 y r2 = λ r1 está dado por:
t2 = λ nt1
(4.6.1)
El valor del exponente, n, está relacionado con el mecanismo específico que controla la densificación y es
igual a 4 para la difusión en borde de grano y difusión superficial, 3 para la difusión volumétrica, 2 para el
transporte de vapor y 1 para la sinterización viscosa.
Además, para partículas más pequeñas es posible reducir la temperatura de sinterización y alcanzar la misma
densidad en el mismo tiempo que en el caso de partículas más grandes que requerirían temperaturas más altas.
Si la densidad relativa, ρ puede expresarse como una función del tiempo y la temperatura, según la expresión:
ρ = te
−Q
kT
(4.6.2)
entonces puede calcularse el cambio en la temperatura de sinterización para lograr la misma densidad relativa
en un tiempo dado por un cambio en el tamaño de partícula.
Una disminución de la temperatura de sinterización puede ser beneficioso para prevenir la descomposición o
evaporación de un material, para reducir el uso de energía e inhibir el crecimiento de grano. Sin embargo, los
cambios en la temperatura de sinterización pueden también provocar variaciones en los mecanismos de
sinterización dominante conduciendo a una microestructura diferente con propiedades diferentes.
8.- Efecto del ángulo diedral.
Esta claro que la forma y la fracción de volumen de poros evolucionan continuamente durante el proceso de
sinterización, y la comprensión de dicha evolución es crítica para entender como puede obtenerse densidades
teóricas altas. Una implícita y fundamental presunción es la existencia de una fuerza motriz para contraer los
poros en todo momento, una presunción que no siempre es válida. Bajo ciertas condiciones, los poros pueden
ser termodinámicamente estables. Para demostrar las condiciones para el cual ese es el caso, se consideran los
cuatro granos que se interceptan como se muestra en la figura 4.6.1.a.
Refiriéndose a dicha figura, si se permite al poro contraer una cantidad igual al área sombreada, la energía en
exceso eliminada es proporcional a 2ΓγSV mientras que la energía en exceso ganada será proporcional a λγGB,
donde Γ y γ están definidas en la figura 4.6.1.a. La relación entre la energía ganada y energía perdida es:
Energía ganada 2Γγ SV
=
Energía perdida λγ BG
(4.6.3)
86
Combinando este resultado con la ecuación:
Φ
γ BG = 2γ SV cos  
2
y el hecho que cos(ϕ/2) =Γ/λ (Figura 4.6.1.a), se puede demostrar que el lado derecho de la ecuación (4.6.3)
es igual a 1, cuando ϕ = φ. En otras palabras, cuando los granos alrededor de un poro encuentran que
Φ

2
γ BG = γ SV cos 
la fuerza motriz para la migración de borde grano y la contracción del poro tiende a 0.
Esa es una conclusión importante dado que implica que si se quieren eliminar completamente los poros, sus
números de coordinación tienen que ser menor que un valor crítico nc. Adicionalmente se demuestra que nc
esta relacionado con el ángulo diedral mediante la expresión:
360
nc >
180-Φ
Basándose en estos resultados, se puede concluir que el incremento del ángulo diedral, en principio, debe
ayudar en los últimos estados de la sinterización. Sin embargo, la situación no es simple, dado que se puede
demostrar también que la avidez de los poros a los bordes de grano es más fuerte para ángulos diedrales más
pequeños. Dado que para eliminar los poros tienen que permanecer adjuntos a los bordes de grano, esta última
propiedad tendería a sugerir que bajos ángulos diedrales ayudarían en la prevención de la separación poroborde y así ser beneficioso. Finalmente, cabe resaltar que la ruptura de canales al final del etapa intermedia de
la sinterización ocurre a fracciones de volumen de poros más pequeñas a medida que el ángulo diedral
decrece, lo que nuevamente es favorable.
Figura 4.6.1.- Efecto de la coordinación del poro sobre su contracción para un sistema donde el ángulo diedral
es φ = π/2. (a).- Intersección de 4 granos alrededor de un poro. (b).- Intersección de 6 granos, esto
es, ϕ =120°. Hay que señalar que para mantener el ángulo diedral de equilibrio, las superficies de
los granos alrededor del poro tienen que ser convexas. (c).- El mismo sistema con ϕ = 60°. Aquí la
superficie del poro tiene que ser cóncava para mantener el ángulo diedral de equilibrio.
87
La figura 4.6.2 presenta la forma de los poros para diferentes valores del ángulo diedral. La curvatura de la
superficie de los poros se incrementa a medida de que el ángulo diedral se incrementa. Cuando un poro está
localizado en la junta de tres o más granos, la curvatura de la superficie del poro se determina por el ángulo
diedral y el número de granos en contacto con el poro. Para un poro de tres lados cuando φ = 60 º el poro
tendrá lados rectos y no habrá una fuerza motriz para la contracción. Por lo tanto, ese ángulo es un ángulo
diedral crítico, φcrít, para la contracción del poro. Para un poro de cuatro lados, φcrítico = 70.5°.
Figura 4.6.2.- Efecto del ángulo diedral y de la razón energía de borde de grano a energía superficial en la
forma de los poros. Ángulos diedrales bajos resultan en poros alargados y ángulos diedrales
altos resultan en poros esféricos.
El ángulo diedral crítico como una función del número de granos circundantes se presenta en la figura 4.6.3.
De esta manera, cuando el ángulo diedral es demasiado bajo, los poros serán estables en la estructura y habrá
una densidad limitante aún cuando la eliminación de los poros reduciría la energía del sistema. A fin de
cuentas, a medida que el crecimiento de grano ocurre el número de granos intersectando el poro decrecerá así
que los poros se convertirán en inestables y contraerán. Sin embargo, a medida que el tamaño de grano se
incrementa, las distancias de difusión se incrementan y la velocidad de contracción baja, haciendo la
eliminación de los poros un proceso relativamente lento.
Figura 4.6.3.- La estabilidad de los poros en el estado final de la sinterización en función del número de
granos que los poros contactan. Los poros con números de lados altos tenderán a ser estables y
permanecerán en la estructura.
88
5.- Sinterización con aplicación de presión externa.
5.1.- Introducción.
Una dificultad común que a menudo surge en la sinterización de cerámicas es la de una densificacion
inadecuada. Una solución para superar dicha dificultad es el uso de una tensión o presión externa al sistema
en polvo duranteel calentamiento, dando lugar a las técnicas de prensado en caliente, el prensado isostatico en
caliente y la forja en caliente.
Los modelos para el prensado en caliente por transporte de masa difusional bajo las fuerzas motrices de la
curvatura superficial y la tensión aplicada fueron formulados por Coble. En una aproximación, los modelos
analíticos para la sinterización fueron adaptados para incluir los efectos de una tensión aplicada, mientras que
en una segunda aproximación, el prensado caliente es visto de una manera análoga a la de la fluencia en
solidos densos y las ecuaciones de fluencia se modifican para tener en cuenta la porosidad y la curvatura
superficial apropiadas al sistemas en polvo.
5.2.- Modelos de prensado en caliente.
Considere los modelos idealizados para las tres etapas de sinterización (Figura 2.1). La concentración de
vacantes bajo la superficie del cuello no se ve afectada por la tensión aplicada de modo que viene dada por la
ecuación:
C γ Ω  1 1  C γ ΩK
(5.2.1)
∆CV = CV − CV 0 = V 0 SV  +  = V 0 SV
kT
kT
 r1 r2 
donde K es la curvatura de la superficie del poro. Para la etapa inicial de sinterización, K = 1/r = 4a/X2,
mientras que para las etapas intermedia y final el valor es K = l/r y 2/r, respectivamente, donde r es el radio
del poro, a es el radio de la partícula y X es el radio del cuello.
La tensión pa, aplicada al sistema en polvo da lugar a una tensión pe sobre el límite de grano y debido a la
porosidad, pe es mayor que pa. Se asume que:
pe = Φpa
(5.2.2)
donde Φ es un factor, denominado factor de intensificación de tensión. La tensión compresiva en el límite de
grano significa que la concentración de vacantes es menor que la correspondiente a un límite plano, sin
tensión, es decir:
C pΩ
C Φp Ω
∆CVB = − V 0 e = − V 0 a
(5.2.3)
kT
kT
Para el modelo de dos esferas, que es el apropiado para la etapa inicial de sinterización (Figura 4.2.1.1),
Coble asumió que Φ es igual al área de la esfera proyectada sobre el punzón del prensado en caliente dividido
por el área de la sección transversal del cuello, es decir:
4a 2
Φ=
πX2
mientras que, tanto para la etapa intermedias como para la final, Coble argumentó que Φ = 1/ρ, donde ρ es la
densidad relativa del cuerpo.
Usando los parámetros para K y Φ, en la figura 5.2.1 se muestra esquemáticamente la variación de ∆CVP y
∆CVB en función de la densidad relativa, ρ. Para el prensado caliente, la diferencia entre la concentración de
vacantes en la superficie de cuello y en el límite de grano:
∆C = ∆CVP − ∆CVB
89
para la etapa inicial viene dada por:
∆C =
4aC0Ω 
ap 
γ + a
2  SV
π 
kTX 
(5.2.4)
Esta ecuación muestra que en la etapa inicial de la sinterización , la ∆C para el prensado caliente es idéntica a
la de la sinterización convencional, pero el termino γSV es substituido por γSV + (apa/π). Puesto que pa y a son
constantes, se tiene que las ecuaciones para el prensado en caliente pueden obtenerse de las ecuaciones de
sinterización simplemente substituyendo γSV por γSV + (apa/π).
Figura 5.2.1.- Fuerza motriz en el prensado en caliente en función de la densidad relativa.
Coble no adaptó expresamente los modelos de sinterización de la etapa intermedia y final para el caso del
prensado caliente, pero usó una aproximación diferente basada en una modificación de las ecuaciones de
fluencia. Por otra parte, si se formulan las ecuaciones diferenciales para el transporte de materia con la
dependencia apropiada del potencial químico sobre la curvatura superficial y la tensión aplicada, entonces la
sinterización y las ecuaciones para el prensado en caliente pueden ser derivadas por el mismo análisis.
90
5.3.- Modificación de las ecuaciones de fluencia.
Se considerará el transporte de materia durante la fluencia de un sólido denso y la forma que las ecuaciones
de fluencia pueden tomar. Comenzamos con un cristal simple de un sólido puro con estructura cúbica que
tiene la forma de una barra con una sección transversal de longitud la L. La tensión normal pa actúa sobre los
lados de la barra como se muestra en la figura 5.3.1.a. Nabarro y Herring argumentaron que la autodifusión
dentro del cristal causará que el sólido se deforme (por ejemplo, por fluencia) en un intento de liberar
tensiones.
La fluencia es debida a los átomos que se difunden de las intercaras sujetas a una tensión compresiva (donde
tienen un potencial químico más alto) hacia aquellas sujetas a una tensión de tracción (potencial químico
inferior). Extendiendo esta idea a la fluencia de un sólido policristalino, la autodifusión dentro de los granos
individuales hará que los átomos se difundan de las fronteras de grano en compresión hacia aquellas que esten
a tensión (Figura 5.3.1.b). La fluencia por difusión de red, comúnmente, se denomina como fluencia de
Nabarro-Herring. Un análisis del flujo atómico por Herring dio para la velocidad de fluencia la ecuación
siguiente:
•
40 DL Ωpa
εc =
(5.3.1)
3 kTG 2
donde:
DL = Coeficiente de difusión de red
Ω = Volumen atómico
pa = Tensión aplicada
G = Tamaño de grano
k = Constante de Boltzmann
T = Temperatura absoluta.
La velocidad de fluencia es, por definición, una velocidad de deformación lineal igual:
1 dL
L dt
(5.3.2)
donde L es la longitud del sólido y t es el tiempo.
La fluencia en un sólido policristalino también puede ocurrir por la difusión a lo largo de las fronteras de
grano (Figura 5.3.1.c), comúnmente denominada fluencia de Coble, y para este mecanismo, la ecuación de
fluencia es:
•
47.5Dgbδ gb Ωpa
εc =
(5.3.3)
kTG 3
donde:
Dgb = Coeficiente de difusión del límite de grano.
δgb = Anchura del límite de grano.
Las ecuaciones (5.3.1) y (5.3.3) tienen la misma dependencia lineal de pa, pero se diferencian en términos de
la dependencia del tamaño de grano y de las constantes numéricas.
91
Figura 5.3.1.- a) Un cristal solo sujetado a una tensión de uniaxial, mostrando a la dirección del flujo atómico.
(b) (y c) un grano típico en un policristalino sólido, mostrando al flujo esperado atómico por
difusión de enrejado (b) y por difusión de límite de grano (c).
La aplicación de una tensión bastante alta, en algunas cerámicas, puede activar el transporte de materia por el
movimiento de dislocaciones. Para este mecanismo, la velocidad de fluencia viene dada por:
•
εc
=
ADµb  pa 


kT  µ 
n
(5.3.4)
donde:
A = Constante numérica
D = Coeficiente de difusión
µ = Módulo de cizalladura
b = Vector de Burgers
El exponente n depende del mecanismo de movimiento de las dislocaciones y tiene valores en el rango de 310.
5.4.- Ecuaciones para el prensado en caliente.
En el prensado en caliente de polvos, los datos, normalmente, se adquieren en forma de la densidad en función
del tiempo a partir de los cuales puede determinarse la velocidad de densificación. Además, la porosidad está
presente de forma considerable durante una gran parte del proceso. La modificación de las ecuaciones de
fluencia derivadas para sólidos densos, por lo tanto, intentan incorporar esos dos factores:
(1).- Relacionar la velocidad de fluencia (Velocidad de deformación lineal) con la velocidad de densificación
(Velocidad de deformación volumétrica)
(2).- Compensando la presencia de porosidad.
92
En el prensado en caliente, la masa M del polvo y el área de la sección transversal A del molde son
constantes. Cuando la densidad D de la muestra aumenta, el espesor de la muestra L disminuye. Las variables
D y L son relacionadas por la expresión:
M
= LD = L0 D0 = L f D f
(5.4.1)
A
donde los subíndices 0 y f se refieren a los valores iniciales y finales. La diferenciación de la ecuación (5.4.1)
con respecto al tiempo da:
dD
dL
L
+D
=0
(5.4.2)
dt
dt
Reorganizando esta ecuación, se obtiene:
−L
dL 1 dD 1 d ρ
=
=
dt D dt ρ dt
(5.4.3)
donde ρ es la densidad relativa.
La ecuación (5.4.3) relaciona la velocidad de deformación lineal del cuerpo durante el prensado en caliente
con la velocidad densificación. La velocidad de deformación lineal, comúnmente, se obtiene midiendo la
distancia recorrida por el punzón del molde del prensado en caliente en función del tiempo.
Para la compensación de la presencia de porosidad en el sistema en polvo, recordaremos la discusión de la
etapa inicial del modelo de Coble para el prensado en caliente en el que la tensión eficaz sobre las fronteras
de grano pe esta relacionada con la tensión aplicada externamente pa por la ecuación (5.2.2). Para considerar
los efectos de la tensión aplicada y la curvatura superficial sobre la velocidad de densificación, Coble
argumentó que la fuerza motriz total (DF) es una combinación lineal de los dos efectos, es decir:
DF = pe + γ SV K = Φpa + γ SV K
(5.4.4)
donde K es la curvatura del poro, igual a 1/r para el modelo de sinterización de la etapa intermedia y 2/r para
el modelo de la etapa final.
Para obtener la ecuación apropiada para el prensado en caliente, DF dado por la ecuación (5.4.4) sustituye a
la tensión aplicada pa en las ecuaciones de fluencia de los sólidos densos. Las ecuaciones para el prensado en
caliente obtenidas por modificación de las ecuaciones de fluencia se resumen en la tabla 5.4.1.
Tabla 5.4.1.- Ecuaciones para el prensado en caliente obtenidas por modificación de las ecuaciones de
fluencia.
93
La modificación de Coble de las ecuaciones de fluencia proporciona sólo una aproximación a la velocidad de
densificación durante el prensado en caliente. Un análisis más riguroso requiere modificaciones adicionales en
los modelos de fluencia para una mejor representación la situación presente en los sistemas en polvo, como
diferencias del campo de flujo atómico y de la longitud del camino para la difusión. En los modelos fluencia,
el flujo atómico termina en las fronteras de grano bajo tensión, mientras que en el prensado en caliente, el
flujo termina en las superficies del poro. El área del límite de grano, que esta relacionada con el tamaño de
grano, permanece constante durante la fluencia, pero tanto el área del límite de grano como la longitud del
camino de difusión aumentan durante el prensado en caliente.
5.5.- Mecanismos
del prensado en caliente.
Los mecanismos analizados con anterioridad para la sinterización también funcionan durante el prensado en
caliente, pero los mecanismos que no densifican pueden despreciarse porque no mejoran por la tensión
aplicada, mientras que los mecanismos que densifican mejoran considerablemente. A causa de la mejora de
los mecanismos que densifican en relación con los mecanismos que no densifican, el prensado en caliente
proporciona una técnica eficaz para determinar el mecanismo de densificación. Sin embargo, pueden activarse
nuevos mecanismos debidos a la tensión aplicada, los cuales pueden proporcionar complicaciones y entonces
su presencia tiene que ser reconocida.
El reordenamiento de las partículas contribuye a la densificación durante la etapa inicial pero es difícil de
analizar. El deslizamiento del límite de grano es necesario para acomodar los cambios de forma controlados
por difusión, que ocurren durante las etapas intermedias y finales de la sinterización. Como se muestra en la
figura 5.5.1 de una sección transversal, un elemento representativo del sistema (por ejemplo, tres granos
idealizados con una forma hexagonal) debe imitar el cambio de forma total del compacto de polvo.
Ya que el diámetro del molde en el prensado en caliente es fijo, la consolidación o compactación del polvo
ocurre predominantemente en la dirección de la presión aplicada, por lo que los granos serán aplanados. Este
cambio de forma debe acomodarse por deslizamiento de unos granos sobre otros. El deslizamiento del límite
de grano y el transporte de masa difusional no son mecanismos independientes, sino que ocurren
secuencialmente de modo que el mecanismo más lento controla la velocidad de densificación. Para resumir,
los mecanismos principales que, comúnmente, operan durante el prensado en caliente son la difusión de red,
la difusión en el límite de grano, la deformación plástica por el movimiento de las dislocaciones, el flujo
viscoso, el reordenamiento y el deslizamiento del límite de grano.
Figura 5.5.1.- Ilustración que muestra el cambio de la forma del grano que ocurre durante el prensado en
caliente. Los granos son aplanados en la dirección de la presión aplicada. Cuando el transporte
de materia ocurre por difusión, el deslizamiento del límite de grano es necesario para acomodar
el cambio de forma del grano
94
Según la tabla 5.4.1, cuando la tensión aplicada es mucho mayor que la fuerza motriz debida a la curvatura
superficial (que corresponde a la situación práctica común), la velocidad de densificación durante el prensado
en caliente puede escribirse en la forma:
1 d ρ HDΦ n n
=
pa
kTG m
ρ dt
(5.5.1)
donde:
H = Constante numérica
D = Coeficiente de difusión de la especie que controla velocidad
Φ = Factor de intensificación de tensión
G = Tamaño de grano
K = Constante de Boltzmann
T = Temperatura absoluta
m y n = Exponentes que dependen del mecanismo de densificación.
La tabla 5.5.1 da los valores de m y n, así como el coeficiente de difusión apropiado para varios mecanismos
que operan en el prensado en caliente.
Tabla 5.5.1.- Mecanismos en el prensado en caliente y exponentes y coeficientes de difusión asociados.
Debido a que mejoran los mecanismos que densifican y se limita el crecimiento de grano, el prensado en
caliente proporciona una técnica eficaz para investigar el mecanismo de densificación. Según la ecuación
(5.5.1) y la tabla 5.5.1, una gráfica de la velocidad de densificación (a densidad fija) en función de pa permite
determinar el exponente n y así el mecanismo de densificación. Para las presiones comúnmente usadas en el
prensado en caliente (típicamente 10-50 MPa), los datos obtenidos para muchas cerámicas dan un valor de
n∼1, sugiriendo que un mecanismo de difusión es el responsable de la densificación. Este resultado no es
sorprendente en vista del enlace químico fuerte presente en las cerámicas, que limitan el movimiento de las
dislocaciones y la tendencia de emplear polvos finos (que favorecen los mecanismos de difusión). Sin
embargo, valores altos de n característicos del mecanismo del movimiento de las dislocaciones se observan en
algunas cerámicas.
El mecanismo dominante de densificación puede cambiarse dependiendo de la presión aplicada, la
temperatura y el tamaño de grano. Por ejemplo, debido al exponente del tamaño de grano más grande (m = 3)
y a la energía de activación, generalmente, inferior, polvos más finos y temperatura más bajas favorecen la
difusión de límite de grano sobre la difusión de enrejado (m = 2). Por selección cuidadosa de las variables de
proceso, puede identificarse el mecanismo dominante bajo un conjunto dado de condiciones y los resultados
comúnmente se muestran en forma de un mapa, denominado mapa del prensado en caliente o mapa del
mecanismo de deformación, análogo a los mapas de la sinterización convencional. En la figura 5.5.2 se
muestra un mapa del prensado en caliente para la α-Al2O3 pura, que da la temperatura en función del tamaño
de grano, mostrando las relaciones entre los mecanismos y parámetros del prensado en caliente.
95
Figura 5.5.2.- Mapa del prensado en caliente (Deformación) para α - alúmina pura.
5.6.- Factor de intensificación de tensión.
En los modelos del prensado en caliente, aparece el factor Φ definido por la ecuación (5.2.2), el cual es
necesario para relacionar la tensión media en el límite de grano pe con la tensión aplicada externamente, pa. El
factor se denomina factor de intensificación de tensión (o factor de multiplicación de tensión). La importancia
de Φ es tal que mientras pa es la tensión que es medida, pe es la parte que le corresponde y que influye en la
velocidad de transporte de materia. El factor Φ es geométrico en origen y es de esperar que dependa de la
porosidad y de la forma de los poros.
Considerando una presión hidrostática pa aplicada a la superficie externa de un sistema en polvo, cuyo modelo
se muestra esquemáticamente en la figura 5.6.1.a. La presión aplicada ejerce sobre la superficie del sólido una
carga aplicada:
Fa = ATpa
(5.6.1)
donde AT es el área total de la sección transversal externa del sólido, incluyendo en tal área la ocupada por
poros. La presencia de porosidad localizada en las fronteras de grano hace que el área real del límite de grano
Ae sea más pequeña que el área total externa. Asumiendo un equilibrio de fuerzas a través de cualquier
sección plana del sólido, se obtiene:
pa AT = pe Ae
(5.6.2)
por lo tanto,
Φ=
pe AT
=
pa Ae
(5.6.3)
Para poros esféricos distribuidos aleatoriamente en sólido un poroso, Φ puede determinarse fácilmente.
Tomando un plano arbitrario en el sólido, la fracción de área en el plano debida a la porosidad es igual a la
fracción de volumen de la porosidad. Si se asume que AT es la unidad, entonces Ae es igual a 1 - P, donde P es
la porosidad del sólido. Puesto que, (1 - P) también es igual a la densidad relativa, se puede escribir:
Φ=
1
ρ
(5.6.4)
96
Esta expresión sería aplicable a un vidrio que contiene poros aislados, casi esféricos o a un sólido
policristalino en el cual las formas de equilibrio de los poros aislados son aproximadamente esféricas (por
ejemplo, para ángulos diedrales mayores que ∼150 °). Cuando los poros se desvían de forma significativa de
la forma esférica, la expresión simple anterior no se mantiene y de hecho, puede esperarse que la expresión
nueva sea bastante compleja. Como se ilustra en la figura 5.6.1 para poros con el mismo volumen pero de
formas diferentes, se puede esperar que Φ dependa no sólo de la porosidad, sino también de la forma de los
poros. Cuando la forma del poro se desvía de la geometría esférica (por ejemplo, al disminuir el ángulo
diedral), el área actual del límite de grano disminuye, por lo que Φ debería aumentar.
Figura 5.6.1.- (a).- La tensión efectiva en el límite de grano pe es mayor que la tensión externa aplicada pa
debido a la presencia de poros en el límite de grano. El factor de intensificación de tensión se define
como la relación entre el área total externa y el área real del límite de grano
(b).- Φ depende de la porosidad, así como la forma de poro, teniendo una dependencia más fuerte
de la porosidad para poros con ángulos diedrales más pequeños, por ejemplo, poros elípticos.
La simulación por ordenador de las formas de equilibrio de una red continua de poros ha sido realizada por
Beeré. Un análisis de los resultados de Beeré realizado por Vieira y Arroyo ha mostrado que Φ puede
aproximarse por la expresión:
Φ = eα P
(5.6.5)
Donde α un es un factor que depende del ángulo diedral y P es la porosidad. En la figura 5.6.2 se muestran en
una gráfica semilogarítmica los resultados de Beeré del factor de intensidad de tensión en función de la
densidad relativa, para varios ángulos diedrales, de la cual se puede determinar el factor α. La ecuación (5.6.5)
ha sido verificada por datos experimentales recientes, pero esto no implica que sea el modelo más exacto o
apropiado.
Figura 5.6.2.- Factor de intensidad de tensión en función de la densidad relativa, para varios ángulos diedrales.
97
Como se resume en la tabla 5.6.1, se han propuesto otras expresiones para Φ, y dependiendo de las
características en polvo y del empaquetamiento, pueden ser apropiadas para ajustar los datos. Una gráfica de
Φ en función de la densidad relativa ρ para varias expresiones (Figura 5.6.3) muestra diferencias grandes
entre los valores. Excepto para el modelo basado en esferas de tamaño uniforme , todos los resultados pueden
ser representados por una función exponencial de la forma dada por la ecuación (5.6.5).
Tabla 5.6.1.- Factor de intensificación de tensión para varias geometrías del polvo.
Figura 5.6.3.- Factor de intensidad de tensión en función de la densidad relativa, para varias geometrías
idealizadas y para los datos de Shima y Oyane.
5.7.- Tensión en la sinterización.
De acuerdo con la tabla 5.4.1, la velocidad de densificación para los mecanismos controlados por difusión
puede escribirse en la forma general:
1 dρ
3 dL 3
=−
=
(5.7.1)
( Φpa + σ )
ρ dt
L dt η ρ
donde (1/L)(dL/dt) es la velocidad de deformación lineal de la sinterización sólida, ηρ tiene las dimensiones
de una viscosidad y puede denominarse viscosidad de densificación y σ es la tensión efectiva sobre los
átomos bajo la superficie del poro dada por la ecuación de Young y Laplace:
1
σ = γ SV 
 r1
+
1

r2 
(5.7.2)
98
donde r1 y r2 son los dos radios de curvatura principales de la superficie de poro. La cantidad σ es la fuerza
motriz termodinámica para la sinterización y tiene las unidades de una presión (o tensión) y a veces se
denomina presión de sinterización o potencial de sinterización.
La ecuación para σ es en realidad más compleja para una cerámica policristalina donde los poros están en
contacto con las fronteras de grano y consiste en dos contribuciones, una atribuida a los poros y la otra a las
fronteras de grano. Por ejemplo, para una microestructura de la etapa final idealizada donde los poros y los
granos se asume que tienen una forma esférica, σ viene dado por la expresión:
σ=
2γ gb
G
+
2γ SV
r
(5.7.3)
donde:
γgb = Energía específica del límite de grano
G = Tamaño de grano
r = Radio de poro.
La fuerza motriz para la sinterización también esta influenciada por el ángulo diedral y el mecanismo de
transporte de masa y ha sido calculada para una geometría simple que consiste en una línea de partículas
esféricas.
La ecuación (5.7.1) también puede escribirse:
1 dρ
3 dL 3Φ
=−
=
( pa + Σ )
ρ dt
L dt η ρ
(5.7.4)
donde Σ = (σ/Φ) tiene las unidades de una tensión y se denomina como la tensión de sinterización. Como el
término Σ, ocurre en una combinación lineal con la tensión externa aplicada pa, puede ser tomado para
representar la tensión externa equivalente aplicada, que tiene el mismo efecto sobre la sinterización que las
superficies curvas de los poros y fronteras de grano. La formulación de la fuerza motriz para la sinterización
en términos de una tensión ficticia aplicada externamente es ventajosa en el análisis de la sinterización, donde
existan efectos debidos a tensiones mecánicas, como es el caso de la sinterización con presión y la
sinterización restringida. También proporciona una base conceptual para diseñar experimentos para medir la
fuerza motriz de la sinterización.
6.- Defectos de sinterizado.
Los siguientes párrafos describen, sucintamente, algunos de los defectos que pueden presentarse en piezas
sinterizadas fabricadas con productos refractarios (cerámicos).
6.1.- Alabeo (warping).
Resulta de un soporte inadecuado de la pieza durante el proceso de sinterización o de variaciones espaciales
de la densidad en el producto en verde (compactado no sinterizado). Se distingue uno de otro por inspección
dimensional de la pieza y examen micrográfico de la sección transversal: el alabeo por fluencia no produce
variaciones de espesor ni modificaciones de la microestructura, sin embargo el alabeo por
variaciones de densidad si. El primero puede eliminarse mediante un soporte correcto de las piezas
en el horno de sinterizado y el segundo, efectuando una compactación correcta del sistemas de polvo.
99
La densidad después de la coccion es casi uniforme, y en la pieza en verde hay una contracción más alta en las
partes con una densidad más baja que en las partes con una densidad alta. En la pieza prensada, las
variaciones de presión en el molde es la causa de las variaciones de consolidación en partes diferentes de la
pieza. En general la contracción en el centro es más grande que en los extremos y, así para una pieza
cilindrica al final se tendrá una forma de reloj de arena (Figura 6.1.1.a).
Otra fuente de alabeo durante la cocción es la presencia de gradientes de temperaturas (Figura 6.1.1.b). Si la
pieza se pone sobre una placa plana y se calienta desde arriba, hay una diferencia de temperatura entre la
parte superior e inferior de la pieza que puede causar una contracción mayor en la parte superior que en la
inferior y dando lugar al correspondiente alabeo. En algunos casos la tensión gravitacional puede ser
suficiente para devolver a la pieza la forma plana, aun cuando la contracción no sea uniforme. La relación
entre la distribución de temperaturas, el alabeo y la deformación bajo las tensiones desarrolladas es
complicada y difícil de analizar cuantitativamente.
Las piezas vítreas también se alabean por el flujo causado por la fuerza de la gravedad. Esto es sobre todo
verdadero para piezas grandes pesados en las se desarrollan sustanciales tensiones. En el conformado de
sanitarios, la superficie superior de un inodoro o de un lavabo (Figura 6.1.1.c) debe diseñarse con una mayor
curvatura que la deseada en el producto final, de modo que el asentamiento que ocurre durante la cocción del
producto produzca la forma final satisfactoria.
Una contribución final al alabeo durante el cocción es la fuerza de fricción o de arrastre de la pieza contra el
setter. Esto significa que la superficie inferior tiende a encoger menos que la superficie superior (Figura
6.1.1.d) La pieza debe diseñarse de modo que la forma final, incluyendo la contracción, sea rectangular.
Figura 6.1.1.- Contracción durante la cocción: (a).- Pieza cilindrica con contracción diferencial debidas a las
variaciones de densidad en la pieza en verde- (b).- Placa con contracción diferencial debida a
gradientes de temperatura (c).- Sanitarios con contracción diferencial debido al asentamiento
por gravedad (d).- Contracción diferencial debida a la fuerza de fricción debida al asentamiento
100
Las dificultades causadas por la contracción diferencial durante la cocción, que originan la distorsión y el
alabeo de las piezas, pueden eliminarse de tres modos:
1.- Cambiando el método de conformado para reducir al mínimo las causas que dan lugar al alabeo.
2.- Diseñando formas que compensen el alabeo.
3.- Estableciendo métodos de cocción que reducen al mínimo los efectos de alabeo.
Una mejora en el método de conformado es obtener uniformidad de la estructura. Esto requiere la eliminación
de gradientes de presión, segregación y otras fuentes de variación de porosidad. El prensado de piezas que
tienen una gran relación entre la longitud y el diámetro del molde origina variaciones de densidad. Las
mezclas prensadas y estrusionadas que tienen una plasticidad baja son en particular propensas a grandes
variaciones de presión y diferencias de densidad.
El colado y la extrusión causan un cierto grado de segregación y diferencias de densidad durante la cocción.
Algún asentamiento puede ocurrir durante el proceso de colado causando variaciones estructurales.
6.2.- Recocido (overfiring).
Resulta de un tiempo (temperatura) excesivo de sinterizado. Origina alabeos, hinchamientos, interacción
química entre las piezas y estructura del horno de sinterizado, y crecimiento exagerado del
tamaño de grano. Los tres primeros defectos se detectan visualmente y el cuarto, mediante pulido,
ataque y observación en el microscopio óptico de reflexión de una sección de la pieza. En bastantes ocasiones, el
recocido produce exclusivamente un crecimiento exagerado del tamaño de grano, lo que repercute
desfavorablemente en su resistencia a la rotura.
6.3.- Quemado de los aglomerados.
Habitualmente se añade al sistema de partículas un aglomerante orgánico con objeto de facilitar su
compactación. Pero si la temperatura - tiempo-atmósfera del proceso de sinterizado no son correctos, puede
quedar un residuo carbonoso en la pieza que ocasione, localmente, condiciones reductoras causantes de
hinchamiento y manchas (cambios de coloración). Se evita este defecto, efectuando un calentamiento lento
hasta la temperatura en que pueda volatizarse el ligante y manteniéndolo a dicha temperatura durante el tiempo
suficiente para su eliminación completa.
6.4.- Transformaciones alotrópicas.
Las transformaciones alotrópicas que pueden sufrir las partículas que componen el compacto poroso, son una
fuente de problemas durante el enfriamiento que sigue al sinterizado, sobremanera si la variación de volumen
que implican es elevada y tiene lugar en un pequeño intervalo de temperaturas. Las transformaciones alotrópicas,
con ser peligrosas, lo son en menor medida cuando tienen lugar por nucleación y crecimiento, que cuando tienen lugar por
cizallamiento (transformaciones por desplazamiento), en ausencia de difusión. Resultan particularmente interesantes,
desde el punto de vista industrial, las anomalías dilatometricas que presentan las variedades alotrópicas de la
silice que son el cuarzo, tridimita y cristobalita, reflejadas en la figura 6.4.1.
101
Figura 6.4.1.- Cambios de volumen en las transformaciones de las variedades alotrópicas de la sílice.
(a).- Estructura del α-cuarzo, (b).- Estructura de la β-cristobalita
Existen varios métodos para determinar si un compacto es susceptible a la fisuración por transformación
alotrópica. Primeramente puede determinarse por difractometría de rayos X la composición mineralógica del
material. Entonces, puede acudirse a los diagramas de equilibrios relativos a dichos constituyentes, al objeto
de verificar si presentan fases alotrópicas, como por ejemplo, las representadas en los diagramas ideales de la
figura 6.4.2. Sin embargo, estos diagramas no aportan información sobre la magnitud del cambio de
volumen acaecido en una transformación alotrópica, por lo que seria necesario acudir, en tercer lugar, al
análisis dilatométrico.
102
Figura 6.4.2.- (a).- Diagramas de equilibrio con solidificación eutéctica, insolubilidad total y
transformaciones alotrópicas del constituyente A en estado sólido.
(b).- Diagramas de equilibrio con solidificación eutéctica, solubilidad parcial y
transformaciones alotrópicas del constituyente A en estado sólido.
103