MOTORES DE CORRIENTE ALTERNA CON COLECTOR

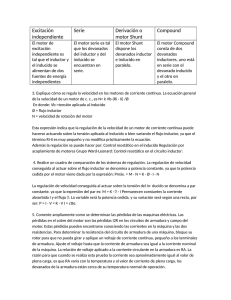
N.° 1. Enero, 1926.
D Y N A
9
Motores de corriente alterna con colector
MOTORES MONOFASICOS
Por Mario Martinez R. de la Escalera — Ingeniero Industrial — Profesor de la Escuela de Ingenieros de Bilbao
Si alimentamos un motor de corriente continua
enviando at inductor una corriente alterna, y otra, en
fase con esta, at inducido, se engendrara un par que
no cambiara de sentido y oscilara, desde un valor
maxim°, a cero, porque el campo magnetico y la corriente en el inducido se invertiran en el mismo instante, y el par, proporcional a su producto, conservara su signo.
Este es el fundamento de los motores e!ectricos
de corriente monofasica con colector, cuya adaptaciOn
industrial ha exigido numerosos trabajos y una gran
perseverancia para resolver los dificiles problemas
que, la aplicaciOn a la practica de una idea tan sencilia, ha originado.
3.a MOTOR SERIE-COMPENSADO 0 SERIEREPULSION (fig. 3. a ) Es una combinaciOn de los
dos anteriores, y en ellos existen (para maquinas bipolares) dos pares de escobillas, alimentadas unas
en serie con el inductor y otras conectadas en corto
circuito.
Tres son las formas generates de estos motores:
1.' MOTOR SERIE (fig. 1. a ) AlimentaciOn por
la misma corriente del inducido e inductor conectados
en serie.
L
FIG.
FIG. 1.'
2. a MOTOR DE REPULSION (fig. 2. a ) UniOn
en corto circuito de las escobillas del inducido y alimentaciOn del inductor por una corriente alterna.
FIG. 2.a
Tanto en este caso como en el primero, el inducido se puede alimentar directamente o por medio de
un transformador en serie con el inductor.
En los tres tipos de motores, el Organ° fijo puede
ser analogo at de las maquinas de corriente continua
con polos salientes o at de los motores asincronos:
el primer sistema reduce el flujo transversal y el segundo da una reparticiOn casi senoidal del flujo en el
entrehierro. En ambos casos debe ser laminar para
evitar las corrientes de Foucault.
El Organo mOvil es un inducido de dinamo o motor de corriente continua, ptro si en estas maquinas
es dificil la conmutaciOn, mucho mas lo sera en los
motores que estudiamos porque las espiras en cortocircuito estan sometidas a la acciOn de un flujo variable ademas de sufrir influencias analogas a las de las
maquinas de corriente continua.
TEORtA DE LOS MOTORES DE COLECTOR
(fig. 4. a ) Establezcamos la teoria en un caso general
en que no tengamos en cuenta la clase de motor y
luego aplicaremos lo que digamos a las .diferentes
especies de motores.
D Y N
10
Supongamos un inducido y un inductor recorridos
por corrientes alternas de intensidades eficaces 4 e
que engendraran los flujos, en fase con estas intensi-
A
N.° 1. Enero, 1926.
ciente de dispersion; y a el angulo de las escobillas
con la normal a los polos avanzada en el sentido del
movimiento; angulo positivo cuando • las •escobillas
estan retrasadas como en la figura y negativo en caso
contrario. Naturalmente, la direccion positiva de
es la misma que la de 42•
Los flujos, 4. y senoidales como las intensidades que los engendran, dan origen a dos fuerzas
electromotrices: una de rotaciOn del conductor en un
campo variable de valor eficaz 4a. que llamaremos Er ;
y otra Ei de inducciOn estatica debida al flujo
La f. e. m. de rotaciOn tiene el valor instantaneo
e= -e- - X N2 X C/9 a X
a
10- 8 volts
valor igual al de la f. e. m. de una maquina de corriente continua con flujo Ya.
A este valor instantaneo corresponde el eficaz:
Er
=a
n, x
X 4). X10- 8 volts
siendo n2 =n.° de revoluciones por segundo.
FIG. 4.'
dades, cuyos valores eficaces (1), y (D 2 se deducen de
las relaciones :
E= 2 X 4 f X X10- 8 volts
X, X 1,25 X- 2p, X = (D i = 2
X2 X
N,, \,
/\
2p 2a — P2 (1) 2 - 2
1,20
(1)
52
en cuyas expresiones :
X1 y X 2 -son ntimeros comprendidos entre 0,7 y 1
(segtin el tipo y arrollamiento del Organ° correspondiente) que tienen en cuenta la composicion geometrica de las fuerzas m.m. de las
diferentes espiras.
N 1 y N2 -son ntimeros de conductores activos en el
inductor e inducido. •
2p—n.° • de polos.
2a—n.° de circuitos en paralelo en el inducido.
P1 y P 2 -reluctancia de los circuitos magneticos de
los flujos (1), y (1) 2 respectivamente.
13 y 3 2 -inducciones en el entrehierro producidas
por los flujos (1), y.(1) 2 respectivamente.
3, y 3 2—espesores ficticios del entrehierro, algo superior al verdadero para tener en cuenta Ia
reluctancia de la parte en hierro de los circuitos magneticos.
En las fOrmulas (1) se supone que la corriente 4
del inductor es la corriente que recorre cada conductor y que 4 es la corriente total en el circuito inducido.
Los dos flujos considerados, proyectados sobre la
lined de las escobillas y su normal, dan los flujos
)
CI a (=--)
`ie w
(=-)
4) COS.
(-) : 1 1 (t'l
La f. e. m. de inducciOn, E, para una espira que
se halle bajo la acciOn de un flujo ,1,), vale
pero en nuestro caso el flujo que atraviesa las distintas espiras es diferente y se reparte senoidalmente en
ellas, por consiguiente la f. e. m. eficaz del arrollamiento sera la suma de una serie de f. e. m. eficaces
cuyos valores estan ligados por una relaciOn senoidal,
y suponiendo un gran numero de conductores en el
arrollamiento inducido, su valor sera el valor media
de las f. e. m. componentes multiplicado por el rimero de espiras.
En definitiva:
2
Ls; =x- x4fx
2
en cuyas formulas, , es el coeficiente de utilizacion
del flujo inductor, igual a la unidad menos el coefi-
N,
4a
/as =
p
a xnxN2x;),..x/0-8[volts
f, es la frecuencia que a su vez es igual al producto
del n.° de pares de polos por el de revoluciones de
sincronismo que Ilamamos n.
La f. e. m. de rotaciOn esta en fase con el flujo
que la engendra y Ia de induccion retrasada 90'; su
re5ultante es la f. c. e. m. en las escobillas.
El flujo en el inductor es:
'1)1 ' (=")
(—) 1 1 2 '1)2 sen a
en que 11 2 es el coeficiente de utilizacion del flujo ri) 2
El flujo (V, engendra una f. e. m. de autoinducciOn
Ei =kX f><Ni X
a
sen. a
,.;),-nx
k,
X 10 -8
volts
es un coeficiente que depende del tipo de inductor
y arrollamiento elegido. Sus valores se encuentran en
cualquier tratado y para polos salientes: k=2,22
N.° 1. Enero, 1926.
11
DYNA
REPRESENTACION GRAFICA. —Supongamos
Para mayor generalidad que las intensidades en el inductor e inducido no estan en fase y sea el angulo
de defasado de ellas. Los flujos 4 y 4), en fase con
las intensidades quedaran representadas en dos rectas OM, y OM, que formen dicho angulo (fig. 5.d)
Del mismo modo, la resultante
de 0E1 y E1 V1 --rill nos da 01/1 vector igual y de
sentido contrario al que representa la diferencia de
potenciales entre los terminales del Organ° fijo.
Los angulos V i OA y V2 OP son los angulos de
fase en el inductor e inducido.
MOTOR CON DOS PARES DE ESCOBILLAS
POR PAR DE POLOS.—En este caso (fig. 6. d ) son
tres los flujos que hemos de tener en cuenta: el del
inductor (pi y los del inducido (p2 y 2 que hemos de
proyectar cuatro veces, dos sobre las lineas de escobillas y dos sobre sus normales respectivas; pero eslineas forman en el motor angulos de
taslineas
36 0
4
p y
en
el tiempo (mejor dicho en el diagrama) formaran angulos de 90°; y los flujos proyectados se reducen a
dos, uno (p d sobre la lined de escobillas aa' que satisfara a la ecuaci-On geometrica
Cl)a
(=) (1;2 (—)
(1)1
COS
a
y otro (pm sobre la linea mm' cuyo valor es
(pm (—) 43 2 (—) :11 (D1 sen a
Como hay flujos en la direcciOn de las escobillas
y en la normal a estas, se engendraran f. e. m. de
inducciOn y de rotaciOn que valdr6n .en las escobillas
FIG. 5.'
Tomemos sobre estas direcciones las magnitudes
0M1 = '1)1 " OM' =
COS
OC =
OP =—;11 41 sen a Y OM., =
OM. =
y OP=— rj, 2 sen a
r`di
a
y hallaremos facilmente los vectores representativos
de los flujos
4)rn y 4): 1 . El primero quedara representado por OC; el segundo por OH, resultante
de OP y OM, y el ultimo por OL, cuyos componentes
son 0M 1 y OP.
Estos flujos crean las tres 1. c. e. m. de que ya
hemos hablado: una de rotaciOn en oposiciOn de
fase con el, representada por el vector OG igual en
magnitud a
mm
Er =
a n2. N2. (pd X 10- 8 volts
= P n. N2.
(pm.
en las escobillas aa'
E' r = Pa n2 N2 (pm. X 10- 8 volts
E'i = P n
N2 43a
Er =—
a- n2 N) (i)a(i)rnX 10- 8 volts
una de inducciOn retrasada 90° con relaciOn al
vector que representa el flujo; en la figura la f. e. m.
Ei es OLI y su valor
E1— a n. N2 . 4),n X 10
-8
volts
Por engendra la f. e. m. retrasada
90° con relaciOn a el y representada en la figura por
el vector 0E1 de magnitud
= k. p. n. N 1. , 10- 8 volts
La resultante, 0E2 , de OG y OU compuesta con
en oposiciOn con 0M2 nos da el vector
OV2 igual y de signo contrario a la diferencia de potencial entre las escobillas.
X 10- 8 volts
E2 V2 = —r2 /2,
FIG. 6.'
X10- 8 volts
D Y N
12
Las de rotaciOn en fase, mejor dicho en oposiciOn
de fase con el flujo que las engendra y las de induction retrasadas 90°.
El flujo en el inductor, 4' i tendra por valor
(1)' 1 (=) (1)1 (—)
4/2 sen a (—) 11- ' 2 tr 2 cos
que darn origen a la f. e. m. de inducciOn
= k. F. N1 .
, 10-8 volts
a
El diagrama en este caso es de la figura 7. 8 en que
los flujos estan representados del siguiente modo: (1)1
por el vector OA; (1)2 por 0M2 y 2 por 0M3 —; en
esta figura se han tornado
OM'1
OP=
OC = -1 i 1 (1)1
y
COS a
(1)1 sen
OP =—V.2
It'2 (V2
a
(1)2
sen a
COS a
Componiendo los vectores OM y , OC se halla
OH8 que representa el flujo 4), ; (1)11, se obtiene hallando la resultante de OP y 0M2 ; y fi, quedara representado por OL cuyos vectores componentes son
PP'1 equipolente a OP, y P' i L que lo es 0M1
A
N.° I. Enero, 1926..
Calculados por , las fOrmulas anteriores los valores
de las f. e. m. se pueden llevar a la figura: Er en oposici6n con OH.; Er en Ids mismas condiciones respecto a OHm;
retrasada 90° con relaciOn a OH.,
y de E' l con igual retraso respecto a OH.. Hallando la
resultante
y Er obtendremos la f. c. e. m. entre las
escobillas m y m' que compuesta a su vez con un
vector igual a la caida ohmmica de tensiOn en oposi
ciOn de fase con la intensidad que la produce nos
darn un vector igual y contrario a la diferencia de potenciales entre m y m'. Procediendo analogamente
con E'1 y Er hallaremos la diferencia de potenciales
entre a y a'
Por Ultimo E1 queda representado por el vector
0E1 retrasado 90° con relaciOn a OL, y componiendo
0E1 con la caida de tensiOn hallaremos la diferencia
de potenciales en el Organ° fijo.
No se han hecho estas construcciones por no
complicar la figura.
PAR MOTOR.—Por el principio de la conservation de la energia, se deduce el par motor total instantaneo de la igualdad.
2 7.112 P— 9,81
er i 2
cos
siendo er la f. c. e. m. de rotaciOn.
El par seria, pues, de la forma
P= K. N2 .--P—
a
rf). i 2
cos T
siendo k, una constante.
Para estudiar esta cantidad, el rendimiento, factor
de potencia, etc., acudiremos ya a los diagramas especiales de cada close de motor que serail objeto de
articulos sucesivos.
MARIO MARTINEZ Y RUIZ DE LA ESCALERA.
Ingeniero Industrial
FIG. 7.'