area : matematicas asignatura: geometria docente: hugo hernan

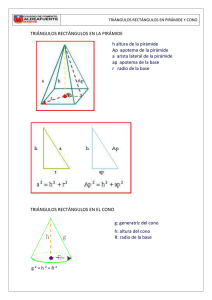
INSTITUCION EDUCATIVA LA PRESENTACION
NOMBRE ALUMNA:
AREA : MATEMATICAS
ASIGNATURA: GEOMETRIA
DOCENTE: HUGO HERNAN BEDOYA
TIPO DE GUIA: CONCEPTUAL - EJERCITACION
PERIODO
GRADO
FECHA
4
9
16 DE SEPTIEMBRE
DURACION
unidades
INDICADORES DE DESEMPEÑO
1. Deduce datos de los gráficos e hipótesis, que permiten crear estrategias de solución a problemas de
sólidos.
2. Emplea los recursos teóricos de la geometría euclidiana y el algebra, para simplificar procedimientos en
la solución de problemas de sólidos.
3. Establece la diferencia entre las características de los sólidos geométricos, para resolver problemas que
involucren el cálculo de áreas y de volúmenes.
4. Realiza las actividades de clase y extra clase con interés, buscando la superación personal.
5. Trabaja en clase y respeta el trabajo de sus compañeras.
CUERPOS GEOMETRICOS (SOLIDOS)
Un Sólido o Cuerpo Geométrico es una figura geométrica de tres dimensiones (largo, ancho y alto), que ocupa
un lugar en el espacio y en consecuencia tiene un volumen.
Es de notar que Los cuerpos geométricos pueden ser: Poliedros y Cuerpos Redondos.
ALGUNAS DEFINICIONES
Poliedro: es un sólido de caras planas (la palabra viene del griego, poli- significa "muchas" y -edro significa
"cara"); es de notar que dichas caras pueden ser polígonos reglares o irregulares.
Caras: Son las superficies planas que forman el poliedro, las cuales se interceptan entre sí.
Arista: Segmento formados por la intersección de dos caras (donde se encuentran dos caras) de un sólido.
Vértice: Punto de intersección de dos o más lados (caras). “esquinas”
Por ejemplo:
Una forma de garantizar que se realizo un buen conteo de los anteriores elementos es utilizar la formula
de EULER o de los POLIEDROS. F + V - E = 2, (F: caras, V: vértice, E: caras)
Angulo diedro: es cada una de las dos partes del espacio delimitadas por dos semiplanos que parten de
una arista común.
El valor de un ángulo diedro es la amplitud del menor ángulo posible que conforman dos semirectas
pertenecientes una a cada semiplano.
Bases: Por lo general son las caras inferiores de un sólido
Polígono: es la región del plano limitada por tres o más segmentos.
Polígonos regulares: triangulo equilátero (3), cuadrado (4), pentágono (5), hexágono
(6), heptágono (7), octágono (8), eneágono (9), decágono (10), endecágono (11),
dodecágono (12). Tridecágono (13), Tetradecágono (14), Icásagono (20).
1
POLIEDROS REGULARES (5)
PIRÁMIDE: Sólido con una sola base poligonal, cuyas caras son todas triangulares y se encuentran en un solo
punto.
PRISMAS: Sólido con dos bases, las cuales son regiones poligonales y congruentes. Sus caras son figuras
planas.
Ejemplos:
CUERPOS REDONDOS “CURVOS”
Son sólidos geométricos que tienen superficies curvas, tales como: el cilindro, el cono y la esfera.
2
OTROS CUERPOS
Tronco de cono
Tronco de pirámide
Vtronco de cono = Vcono grande - Vcono pequeño
Vtronco de pirámide = Vpirámide grande - Vpirámide pequeña
TORO
CONSTRUYENDO LOS POLIEDROS REGULARES
Hexaedro o cubo
Icosaedro
Tetraedro
Octaedro
Dodecaedro
Ejemplos:
1. Calcular la diagonal, el área lateral, el área total y el volumen de un cubo de 5 cm
2
2
3
de arista. R/: d = 5 3 cm, AL = 100cm , AT = 150cm , V = 125cm
2. Calcula el volumen de un cono cuya altura mide 4 cm y el radio de la base es de 3 cm.
3
R/: V= 37,70cm
3. Calcula el volumen de un cono cuya generatriz mide 13 cm y el radio de la base es de 5 cm.
3
R/: V= 314,159cm
4. ¿Cuántos peces, pequeños o medianos, se pueden introducir en un acuario cuyas medidas interiores son
88 x 65 x 70 cm? (Se recomienda introducir, a lo sumo, un pez mediano o pequeño cada cuatro litros de
3
agua) La capacidad del acuario es: V= 85·65·70 = 386.750 cm = 386,8 litros. R/: Se pueden introducir
96 peces
3
5. La base de un prisma es hexágono de lado 1,7cm y apotema 1,5cm. Calcula su volumen sabiendo que su
3
altura es 3,9cm. R/: V = 29,83 cm
6. ¿Cuántas cubetas cilíndricas de agua, de 47 cm de altura y 16 cm de radio, se tienen que vaciar en una
piscina de 10x6x1,5 m para llenarla? 2381 cubetas de agua
7. Se introduce una bola de plomo, de 1 cm de radio, en un recipiente cilíndrico de 3,1 cm de altura y 1,5 cm de
radio. Calcula el volumen de agua necesario para llenar el recipiente. R/: Para llenar el recipiente, hay que
añadir: 21,91 – 4,19 = 17,72 cm3
8. Calcula el volumen de un tronco de cono de 6,1 cm de altura, sabiendo que los radios de sus bases son
6,1 cm y 3,8 cm.
9. Calcula el área y el volumen de un tetraedro de 5 cm de arista.
10. Calcula el área y el volumen de un octaedro de 5 cm de arista.
ACTIVIDAD
I. Dibujar los siguientes solidos:
a. Un hexaedro o cubo, paralelepípedo recto, paralelepípedo oblicuo, un tetraedro, una pirámide de base
cuadrada, un cilindro, una esfera y un cono.
II. Resolver los siguientes ejercicios, realizando las graficas de acuerdo a la exigencia o necesidad.
1. Hallar el Área Total de un prisma cuadrangular que tiene de lado de la base 3 cm y de altura del prisma 5
cm.
2. Hallar el Volumen de una pirámide cuadrangular que tiene de lado de la base 8 cm y de altura de la piramide
6 cm.
3. La base de una pirámide es un pentágono de lado 1,3 cm y apotema 0,9cm. Calcula su volumen sabiendo
3
que su altura es 2,7cm. V = 2,64 cm
4. La Gran Pirámide de Giza es la única que perdura de las siete maravillas del mundo antiguo. Actualmente
tiene una altura de 137 m y la base es un cuadrado de 230 m de lado. ¿Cuál es su volumen aproximado?
3
V = 2.415.767 m
5. Hallar el Área Lateral de un cilindro que tiene de radio de la base 10 cm y de generatriz 5 cm.
3
6. Se echan 7 cm de agua en un recipiente cilíndrico de 1,3 cm de radio. ¿Qué altura alcanzará el agua? h =
1,32 cm
7. Hallar el Área Lateral de un cono que tiene de radio de la base 15 cm y de generatriz 10 cm.
8. ¿Cuántas copas se pueden llenar con 6 litros de refresco, si el recipiente cónico de cada copa tiene una
altura interior de 6,5 cm y un radio interior de 3,6 cm? 68 copas
9. Un cubo de 20 cm de arista está lleno de agua. ¿Cabría esta agua en una esfera de 20 cm de
radio?
10. ¿Cuál es el volumen del cono generado por la rotación de un triángulo rectángulo isósceles, en torno a uno
de sus catetos de longitud 3 cm?
“LAS ÚNICAS PERSONAS NORMALES SON LAS QUE UNO NO CONOCE BIEN”
4
11. Calcula el área y el volumen de un dodecaedro de 10 cm de arista, sabiendo que la
apotema de una de sus caras mide 6.88 cm.
12. Calcula el área lateral, el área total y el volumen de un prisma cuya base es un rombo de
diagonales 12 y 18 cm.
13. Calcula el área lateral, total y el volumen de una pirámide cuadrangular de 10 cm de arista
básica y 12 cm de altura.
14. Hallar el Área y el volumen de una Esfera tiene de radio de la base 10 cm.
15. Calcula el área lateral, total y el volumen de una pirámide hexagonal de 16 cm de arista
básica y 28 cm de arista lateral.
Calcular el volumen de una semiesfera de 10 cm de radio.
16. Calcular el área lateral, el área total y el volumen de un tronco de pirámide cuadrangular
de aristas básicas 24 y 14 cm, y de arista lateral 13 cm.
17. Calcular el área del círculo resultante de cortar una esfera de 35 cm de radio mediante
un plano cuya distancia al centro de la es fera es de 21 cm.
18. Calcular el área y el volumen de una esfera inscrita en un cilindro de 2 m de altura.
19. Un cubo grande esta formado por 27 cubitos iguales; si pintamos la figura exteriormente. ¿Cuántos cubitos
quedan pintados por una sola cara?
20. Otro cubo grande esta formado por 64 cubitos iguales; si pintamos la figura exteriormente. ¿Cuántos
cubitos quedan pintados por tres caras exactamente?
21. Una gota de agua cae en un recipiente cubico, de arista (lado) 10cm, si el nivel del agua se incrementa en
0,2cm, ¿Cuál es el volumen de la gota de agua?
Web grafía
http://claribelsoto.tripod.com/index.htm
http://recursostic.educacion.es/secundaria/edad/2esomatematicas/2quincena10/2esoquincena10.pdf
“NI EL PEOR ENEMIGO TE PUDE HACER TANTO DAÑO COMO TUS PROPIOS
PENSAMIENTOS”
Papá Jaime.
5