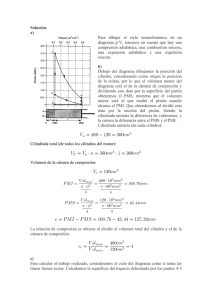
Capitulo 3

Física II: Termodinámica, ondas y fluidos
Índice
3 – LA PRIMERA LEY DE LA TERMODINÁMICA ....................................................................................2
3.2 S ISTEMAS Y PROCESOS TERMODINÁMICOS..................................................................................................2
3.3 T RABAJO REALIZADO A CAMBIAR EL VOLUMEN.........................................................................................3
Ejemplo 3.1 Expansión isotérmica de un gas ideal.........................................................................................4
3.4 CAMINOS ENTRE ESTADOS TERMODINÁMICOS ...........................................................................................5
3.5 ENERGÍA INTERNA Y LA PRIMERA LEY DE LA TERMODINÁMICA ..............................................................6
Ejemplo 3.2 – Quemar el postre.......................................................................................................................8
Ejemplo 3.3 – Diagrama pV .............................................................................................................................9
Ejemplo 3.4 Trabajo en diagrama pV..............................................................................................................9
Ejemplo 3.5 Termodinámica del agua hirviendo.......................................................................................... 10
5.6 CLASES DE PROCESOS TERMODINÁMICOS.................................................................................................11
5.7 ENERGÍA INTERNA DE GAS IDEAL................................................................................................................ 13
5.8 CAPACIDAD CALORÍFICA DE UN GAS IDEAL ............................................................................................... 14
Ejemplo 3.6 Enfriamiento de una habitación................................................................................................ 17
3.9 PROCESOS ADIABÁTICOS PARA UN GAS IDEAL........................................................................................... 18
Ejemplo 3.7 Compresión adiabática en un motor diesel .............................................................................. 21
Ejemplo 3.8 Trabajo efectuado en motor diesel............................................................................................ 22
PROBLEMAS ......................................................................................................................................................... 23
1
3 – La primera ley de la termodinámica
3.2 Sistemas y procesos termodinámicos
Sistemas termodinámicos – sistema que puede interactuar (o intercambiar energía) con
su entorno – 2 formas = trabajo W + calor Q
Procesos termodinámicos – cambios de estado del sistema
Tanto W que Q puede ser positivo o negativo
•
Q > 0 flujo de calor hacia el sistema - energía entra en el sistema
•
W > 0 el sistema hace un trabajo sobre su ambiente – energía sale del sistema
2
3.3 Trabajo realizado a cambiar el volumen
Consideramos un gas en un cilindro con un pistón móvil ⇒ ejemplo censillo de un
sistema termodinámico
Al expandir se en el cilindro elgas empuja la superficie de sus fronteras que se mueven
hacia afuera ⇒ W > 0el gas hace un trabajo sobre su ambiente – el principio también se
aplica a sólido o líquido
•
Suponga un área transversal del cilindro A y una presión p , la fuerza del gas sobre
el pistón será F = pA
•
El pistón se mueve de una distancia dx y el gas hace un trabajo W = Fdx = pAdx
•
De otro lado el incremento de volumen será dV = Adx
(3.1)
dW = pdV
Para un cambio finito de volumen:
(3.2)
W=
V2
∫ pdV
V1
A presión constante:
(3.3)
W = p (V2 − V1 )
Y a volumen constante W = 0
También W > 0 el gas se expande y W < 0 el gas se contracta
Si la presión es variable, se usara un grafico pV - la ecuación 3.2 corresponde al área
debajo de la curva de variación de p en función de V
3
Ejemplo 3.1 Expansión isotérmica de un gas ideal
El gas cambia de volumen de V1 a V2 a temperatura constante T
Usando la ecuación 3.2
V2
W = ∫ pdV
V1
Usando la expresión p =
nRT
tenemos que
V
W = nRT ∫
V2
V1
dV
V
= nRT ln 2
V
V1
Como el gas se expande V2 > V1 y W > 0 el sistema hace un trabajo sobre su entorno
Como T es constante también tenemos la relación siguiente:
V
p
p1V1 = p2V2 o bien 2 = 1
V1 p 2
Por lo tanto:
W = nRT ln
p1
p2
Como el gas se expande p 2 < p1 y por lo tanto W > 0
4
3.4 Caminos entre estados termodinámicos
Camino – cambio de un estado inicial a estado final – puede haber multitud de manera
(estados intermediarios continuos) de llegar al mismo estado
El trabajo realizado por el sistema depende del camino – no solamente del estado inicial
y final
Vimos también que Q el cambio de calor es equivalente a un trabajo mecánico – por lo
tanto también Q depende del camino
Ej. Un gas en expansión libre (b) no hace trabajo – a la diferencia de un gas en expansión a
temperatura constante en un cilindro con un pistón (a) – los dos estados final tie ne mismo
volumen y temperatura – los dos estado finales son similares – pero llegamos a este con
caminos diferentes
⇒ Un Ciclo – estado inicial = estado final, pero esto no quiere decir que W o Q son ceros
durante el ciclo
5
3.5 Energía interna y la primera ley de la termodinámica
La energía interna ( U ) de un sistema es la suma de las energías cinéticas de todas sus
partículas constituyentes, más la suma de todas las energía potenciales de interacciones
entre ellas
IMPORTANTE – no incluye interacción con entorno
Durante un cambió de estado del sistema la energía interna puede cambiar de valor inicial
U1 a un valor final U 2 y se denota el cambio como: ∆U = U2 − U1
Si agregamos calor a un sistema, sin realizar trabajo, la energía interna aumenta de
∆U = Q
Si el sistema efectúa un trabajo W (expansión sobre entorno) sin agregar calor, sale energía
del sistema y el cambio de energía interna es ∆U = −W
En general: primera ley de la termodinámica
(3.4)
∆U = Q − W
(3.5)
Q = ∆U + W
A agregar calor, parte de la energía permanece en el sistema y otra parte puede efectuar
un trabajo
La primera ley de la termodinámica = generalización del principio de la conservación de
energía ⇒ incluye la transferencia de energía como calor equivalente al trabajo mecánico
•
En todas las situaciones en que se parecía que la energía total no se conservara ha
sido posible identificar nuevas formas de energía tal que la energía total esta
conservada (Ej. eléctrica ∝ E 2 , magnética ∝ B 2 , relativista (fusión) E = mc2
Aunque U = ∑ K + ∑ P microscópica, no se puede calcular la energía de este modo ⇒
la descripción no es operativa = no se describe como determinar la energía a partir de
cantidades físicas que no podamos medir directamente
Pero la definición termodinámica ∆U = Q − W es operativa porque podemos medir
Q y W , pero solamente define ∆U no U
•
No hay problema (similar a potencial) – definimos que la energía interna de un
sistema tiene un cierto valor en alguien estado de referencia y luego usamos
∆ U para definir la energía interna en cualquier otro estado
6
Si bien Q y W dependen del camino ∆U no depende del camino ⇒el cambio de energía
interna de un sistema durante un proceso termodinámico solamente depende del esta do
inicial y final
Como U → U ( p, V, T ) el cambio de energía depende solamente de estado del sistema
Dos procesos importantes:
1. Cíclico – el estado inicial es igual al estado final ⇒ U2 = U1 y Q = W
2. Sistema aislado – no realiza trabajo ni cambia calor con su entrono Q = W = 0 y
∆U = 0
El ejemplo arriba del cuerpo humano no es realista ⇒ no es proceso cíclico – durante l
a vida crecen órganos y músculos (aumenta masa) – también los múltiples procesos
físicos-químicos son irreversibles ⇒ el sistema aumenta en entropía = el cuerpo
envejece y muera
Cambios infinitesimales:
(3.6)
dU = dQ − dW
(3.7)
dU = dQ − pdV
7
Ejemplo 3.2 – Quemar el postre
¿Cuantos tramos de escalera debe subir para quemar las 900 calorías que gano comiendo
un postre si su masa es de 60 kg?
Sistema = Usted + Tierra
1 caloría = 4190 J
Asumimos eficiencia de conversión de energía alimentaría de 100%
La energía ingerida:
Q = 900 kcal ⋅ 4190
J
= 3.77 ×10 6 J
kcal
Para subir a una altura h se necesita hacer un trabajo contra la gravedad de la Tierra:
W = mgh = 60 kg ⋅ 9.8
m
⋅ h = 588 N ⋅ h
s2
Para que el estado final sea igual al estado inicial se necesita que W = Q
h=
Q 3.77 × 106 J
=
= 6410 m o 6.4 km
mg
588 N
No es tan fácil quemar esta energía
8
Ejemplo 3.3 – Diagrama pV
La figura muestra un proceso cíclico – el trabajo total es W = −500 J
El trabajo es igual a la superficie debajo del camino – el trabajo en el tramo ab (expansión)
es más chico que en el camino ba (compresión) por lo tanto W < 0 - el entorno hace un
trabajo sobre el sistema
Como el proceso es cíclico ∆U = 0 ⇒ Q = W = −500 J debe salir esta cantidad de calor
del sistema
Ejemplo 3.4 Trabajo en diagrama pV
En el proceso ab se agrega 150 J de calor al sistema – en el proceso bd
600 J
Como no hay cambio de volumen en el proceso ab
W = 0 ⇒ ∆U = Q = 150J
El proceso bd se efectúa a presión constante así que
W = p (V2 − V1 ) = ( 8.0 × 10 4 Pa )( 5.0 × 10 −3 m 3 − 2.0 × 10 −3 m 3 ) = 240J
Por lo tanto ∆U = Q −W = 600J − 240J = 360J
El cambio total de energía durante el proceso abd es: ∆U = 150J + 360J = 510J
Como ∆U es independiente del camino durante el proceso acd ∆ U = 510J
Pero ahora el trabajo debe ser diferente, sobre el tramo ac:
W = p (V2 − V1 ) = (3.0 × 104 Pa )( 5.0 ×10 −3 m 3 − 2.0 ×10 −3 m 3 ) = 90J
Por lo tanto el cambio de calor debe ser Q = ∆U +W = 510J + 90J = 600J
Siguiendo este camino el trabajo es menor y la cantidad de calor más baja que siguiendo el
otro camino
9
Ejemplo 3.5 Termodinámica del agua hirviendo
Necesitamos calcular el trabajo efectuado y el aumento de energía interna cuando 1 g de
agua (1 cm3) se convierte en 1671 cm 3 de vapor a presión constante de 1 atm
( 1.013 × 10 5 Pa).
El calor de vaporización es Lv = 2.256 × 106
(
J
kg
)(
)
El trabajo es W = p (V2 − V1 ) = 1.013× 105 Pa 1671× 10−6 m3 − 1×10−6 m3 = 169J
El calor agregado al agua es el de vaporización:
Q = mLv = 10−3 kg ⋅ 2.256 × 106
J
= 2256J
kg
El cambio de energía interna esta igual por lo tanto a:
∆U = Q −W = 2256J − 169J = 2087J
El aumento de energía interna se asocia por mayor parte a las fuerzas moleculares que
mantienen junta a las moléculas en el estado líquido
Estas fuerzas son atractivas así que las energías potenciales correspondientes son mayores
después de que se hay realizado trabajo para separar las moléculas y formar vapor
Es como aumentar la energía potencial gravitatoria de un elevador alejándolo de l centro de
la Tierra
10
5.6 Clases de procesos termodinámicos
Tiene 4 clases específicos de procesos termodinámicos
1. Adiabáticos – sin transferencia de calor
2. Isobáricos – sin cambio de presión
3. Isotérmico s – sin cambio de temperatura
4. Isocóricos – sin cambio de volumen
Proceso adiabático – sistema aislado o donde el cambio es demasiado rápido para
permitir cambio de calor
(3.8)
∆U = U2 − U1 = −W
Expansión W > 0 la energía interna del sistema diminuye – el sistema hace trabajo sobre
su entorno
Compresión W < 0 la energía interna del sistema aumenta – el entor no hace un trabajo
sobre el sistema
En general, ∆U > 0 implica que T aumenta – el calor especifico es positivo
Ej. motor a explosión – la compresión es casi adiabática - T aumenta a comprimir mezcla
aire + combustible – la expansión es también adiabática con descenso de T
Proceso isocórico – el trabajo W = pdV = 0
(3.9)
∆U = U2 − U1 = Q
Toda la energía agregada en forma de calor se queda dentro del sistema
Ej. calentar un volumen cerrado constante de sustancia
11
Proceso isobárico – W ≠ 0
(3.10)
W = p (V2 − V1 )
Ej. Hervir agua a presión constante
Proceso isotérmico – todo cambio de calor con el entorno debe se producir con lentitud
tal que se mantenga el equilibrio térmico
Como para un gas ideal U → U ( T ) entonces tenemos que ∆U = 0 o sea Q = W toda la
energía que entre en el sistema debe salir con trabajo
Para sustancia no ideal U → U ( p, T ) ⇒ ∆U ≠ 0
La figura muestra un diagrama pV para cada uno de los 4 procesos para una cantidad
constante de gas ideal
Para el proceso adiabático Q = 0 , por lo tanto una aumentación de volumen baja la
temperatura
Para el isocórico W = 0 y una baja de presión produce una baja de temperatura
Para el proceso isotérmico ∆U = 0 y la presión disminuye a medida que se expande el
gas
Solamente aumenta la temperatura durante la expansión isobárica
12
5.7 Energía interna de gas ideal
Par un gas ideal vamos a mostrar que U → U (T )
Consideramos un gas en expans ión libre (ver figura) – no hay agregación de calor y este
gas no hace un trabajo por lo tanto Q = 0 , W = 0 y ∆U = 0
Esto también esta correcto para cualquier sustancia – no solamente gas ideal
Si durante esta experiencia T cambia, pero no U entonces tenemos que U (T ,V ) o
U ( T , p ) , pero si T no cambia, entonces U → U (T )
La experiencia muestra exactamente esto: un gas ideal (gas con baja densidad) en
expansión libre no produce cambio de temperatura ⇒ U → U (T )
La energía interna de un gas ideal depende solamente de su temperatura
Un gas no ideal (o alta presión y baja temperatura), del otro lado, tiene ∆T ≠ 0 durante su
expansión por lo tanto U ( T, p) : las fuerzas intermoleculares cuando se expande el gas
aumenta la energía potencial y la energía cinética disminuye ∆T < 0 el gas se resfría
13
5.8 Capacidad calorífica de un gas ideal
Ya conocemos dos variantes de la capacidad calorífica molar – a volumen constante CV y
a presión constante C p
Pero si ni p o V son constante tiene una infinidad de capacidades caloríficas
¿Del otro lado, porque CV es diferente de C p ?
La respuesta la da la primera ley de la termodinámica:
•
En un aumento de temperatura con V constante, el sistema no efectúa trabajo y el
cambio de energía interna ∆ U es igual al calor agregado Q
•
En un aumento de temperatura con p constante, V debe aumentar si no
T
p = nR no podría ser constante
V
⇒ A expandir se, la sustancia hace un trabajo
(3.11)
Q = ∆U + W
Para un aumento de temperatura dado el cambio de energía interna de un gas ideal tiene el
mismo valor sin importar el camino – por lo tanto esta ecuación indica que el aporte de
calor a presión constante debe ser mayor que para un volumen constante porque se
requiere energía adicional para el trabajo
Por lo tanto C p > CV del orden de 40%
En el caso del agua, el volumen disminuye durante el calentamiento entre 0o C y
4 o C ⇒ W < 0el aporte de calor es menor que en el caso de volumen constante y C p < CV
14
Relación entre C p y CV para los gas es ideales
Consideramos un proceso a volumen constante:
•
colocamos n moles a temperatura T en un recipiente de volumen V y pongamos el
recipiente en contacto térmico con un cuerpo más caliente
•
Una cantidad de calor dQ fluye hacia el gas y su temperatura aumenta dT
dQ = nCV dT
(3.12)
•
La presión aumenta, pero el gas no hace trabajo dW = 0
dU = Q = nCV dT
(3.13)
Consideramos ahora un proceso a presión constante:
•
Cilindro con pistón movible – el pistón se mueve apenas lo suficiente para guardar
la presión constante
•
Pongamos el sistema en contacto con un cuerpo caliente
•
A fluir el calor hacia el gas, ele se expande y efectúa un trabajo dW = pdV
dQ = nC p dT
(3.14)
•
(3.15)
En términos de temperatura
dW = pdV = nRdT
Substituimos 3.14 y 3.15 en la expresión para la primera ley: dQ = dU + dW
(3.16)
nC p dT = dU + nRdT
Donde el cambio de energía interna es igual al dado por la ecuación 3.13 (porque U ( T ) ):
nC p dT = nCV dT + nRdT
(3.17)
C p = CV + R
15
Resulta que muchos gases reales a presión moderada se ajustan a la relación por gases
ideales
Vemos en la tabla que las diferencias son muy cerca de R = 8.315
J
mol ⋅ K
La capacidad calorífica molar de un gas esta relacionada con su estructura molecular – la
última columna de la tabla da la relación entre calores específicos
γ=
(3.18)
Cp
CV
Como C p > CV ⇒ γ > 1
Esta cantidad desempeña un papel importante en los procesos adiabáticos
Segundo la teoría cinética CV =
Cp
3
3
5
R por lo tanto C p = CV + R ⇒ C p = R + R = R
2
2
2
5 2R
= 1.67 muy cerca de las valores medidas para ga ses monoatómicos
CV 3 2 R
5
7
Para mayor parte de los gases biatómicos a temperatura constante CV = R ⇒ C p = R
2
2
7 2R
yγ=
= 1.40
5 2R
Así γ =
=
Recuerda que ∆U = nCV ∆ T que V sea constante o non
16
Ejemplo 3.6 Enfriamiento de una habitación
Tiene 2500 moles de aire en una habitación típica
Consideramos el aire con un gas ideal (γ = 1.40) y calculamos el cambio de energía a
presión constante cuando la temperatura baja de 23.9o C a 11.6 o C (usando un aire
acondicionado)
Forma más fácil de llegar a la respuesta
Para cualquier gas ∆ U = nCV ∆T
Implica que solo necesitamos obtener CV
De la ecuación 3.17 y 3.18 tenemos que γ =
⇒ CV =
Cp
CV
=
CV + R
R
= 1+
CV
CV
R
8.315
J
J
=
= 20.79
γ − 1 1.400 − 1mol ⋅ K
mol ⋅ K
J 
Entonces ∆U = nCV ∆T = ( 2500 mol )  20.79
(11.6K − 23.9K ) = − 6.39 × 10 5 J
mol ⋅ K 

Otro método más complejo:
Determinar el cambio de volumen y determinar el trabajo W = p∆ V
Determinar el cambio de calor a partir de Q = nC p ∆T
Usar la primera ley ∆U = Q − W
17
3.9 Procesos adiabáticos para un gas ideal
Un proceso es aproximadamente adiabático si el sistema es bien aislado u ocurre con tal rapidez que
no hay tiempo para que ocurra un flujo de calor apreciable
Durante un proceso adiabático Q = 0 y ∆U = −W
En la figura consideramos una expansión de Va a Vb ⇒ W > 0por lo tanto la energía interna
diminuye y la temperatura baja
Si el punto (a) esta en un isoterma T + dT el punto (b) será en un isoterma con T
Por un gas ideal la curva adiabática siempre es más espinada que la isoterma
Durante la compresión adiabática la situación invierte y la temperatura aumenta
•
El aire de tubos de salida de los compresores de aire usados en gasolineras o los equipos para
pintar con pistola o para llenar los tanques de buceo siempre es más caliente que el aire que
entra el compresor ⇒compresión rápida casi adiabática
•
Al inversa – enfriamiento adiabático – a abrir una botella gaseosa, el gas que se encuentra
justo por encima de la superficie del líquido se expande rápidamente ⇒ expansión rápida
casi adiabática – la temperatura baja tanto que el vapor de agua se condensa formando nube
18
IMPORTANTE en todos estos procesos calentar y enfriar implica suba o baja de temperatura
⇒ esto se debe al trabajo no al flujo de calor
•
Para cualquier proceso adiabático o non tenemos dU = nCV dT
•
El trabajo dW = pdV
nCV dT = − pdV
(3.19)
Si eliminamos p usando la ley de los gases ideales
nRT
⇒ nCV dT = −
dV
V
dT R dV
⇒
+
=0
T CV V
Pero como
(3.20)
R C p − CV C p
=
=
− 1 =γ −1
CV
CV
CV
dT
dV
+ ( γ − 1)
=0
T
V
Como γ > 1 ⇒ γ − 1> 0 ⇒ dV y dT siempre tienen signos diferentes
•
Expansión adiabática dV > 0 produce baja de temperatura dT < 0
•
Compresión adiabática dV < 0 produce una aumentación de la temperatura
dT > 0
Para cambios finitos de temperatura podemos integrar 3.20
ln T + ( γ − 1) ln V = constante
⇒ ln TV γ −1 = constante
(3.21)
TV γ −1 = constante
Entonces para dos estados inicial T1V1 y final T2V2
(3.22)
T1V1γ −1 = T2V2 γ −1
19
También podemos convertir 3.21 en una relación entre p y V
pV γ −1
V = constante
nR
pV γ = constante
(3.23)
Entonces para dos estados inicial p1V1 y final p 2V2
p1V1γ = p2V2γ
(3.24)
También podemos calcular el trabajo efectuado por un gas ideal durante un proceso
adiabático Q = 0 y W =−∆U usando ∆U = nCV ( T2 − T1 )
W = nCV ( T1 − T2 )
(3.25)
Usando pV = nRT
(3.26)
W=
CV
1
( pV
( pV
1 1 − p 2V2 ) =
1 1 − p 2V2 )
R
γ −1
Si el proceso es una expansión la temperatura baja T1 > T2 ⇒ p1V1 > p 2V2 el trabajo es
positivo
Una compresión produce el inversa W < 0
Las condiciones de validad de las ecuaciones 3.22, 3.24 y 3.26 son
1. que los procesos son bastante rápido como para evitar intercambio de calor
apreciable con el entorno Q = 0
2. pero bastante lento como para que el sistema no se aleja mucho del equilibrio
térmico y mecánico
También ecuaciones son validas de manera aproximativa fuera de estas condiciones
20
Ejemplo 3.7 Compresión adiabática en un motor diesel
La relación de compresión de un motor diesel es de 15 – el aire de los cilindros se
comprime a 115 de su volumen inicial (V1 V2 = 15 )
Vamos a calcular la presión y temperatura del aire comprimida cuando la presión inicial es
1.01 × 10 5 Pa y T = 300K
En su mayor parte el aire es una mezcla de oxígeno y nitrógeno biatómicos (asumimos un
gas idea con γ = 1.40 )
Usando la ecuación 3.22:
γ −1
V 
T2 = T1  1 
 V2 
= ( 300K ) (15 )
0.4
= 886K
Usando la ecuación 3.24
γ
V 
1.40
p 2 = p1  1  = (1.01 × 10 5 Pa ) (15 ) = 44.8 ×10 5 Pa = 44atm
 V2 
Si la compresión hubiera sido isotérm ica la presión final habría sido mucho menor 15atm
Pero con la temperatura aumenta durante una compresión adiabática la presión aumenta
mucho – esta alta temperatura permite al gas encender se espontáneamente
21
Ejemplo 3.8 Trabajo efectuado en motor diesel
Si el volumen del cilindro es inicialmente V1 = 1.00L = 1.00 ×10 −3 m 3 cual es el trabajo
efectuado durante la compresión
Usando pV = nRT determinamos primero la cantidad de moles
n=
5
−3
3
p1V1 (1.01 × 10 Pa )(1.00 × 10 m )
=
= 0.0405mol
RT1
( 8.315J mol ⋅ K )( 300K )
NOTA Pa =
N
Pa 1
y J = N ⋅ m por lo tanto
=
2
m
J m3
Usando la ecuación 3.25:
J 

W = nCV ( T1 − T2 ) = ( 0.0405mol )  20.8
( 300K − 886K ) = −494J
mol ⋅ K 

El trabajo es negativo porque el gas se comprima – el entorno hace un trabajo sobre el gas
Otra manera de determinar el trabajo es de usar directamente la formula
W=
1
( p1V1 − p2V2 )
γ −1
22
Problemas
23
24
25
26
27
28