Nota sobre la elasticidad precio-demanda Ideas básicas

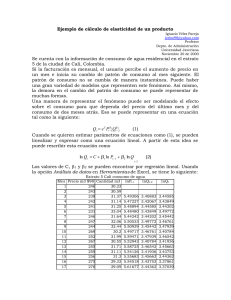
Nota sobre la elasticidad precio-demanda
Ignacio Vélez Pareja
[email protected]
Facultad de Ingeniería Industrial
Politécnico Grancolombiano
Septiembre 2002
Ideas básicas sobre elasticidad precio-demanda
Aunque no es posible generalizar sobre lo que determina la elasticidad
precio-demanda, se pueden identificar, sin ser exhaustivo, algunas de sus
causas y contextos. A continuación se presenta una lista de causas y
circunstancias que pueden afectar la demanda. Se supone que estas
variables actúan en condiciones que los economistas llaman ceteris
paribus. Esto es, se supone que el resto del mundo no cambia.
1. Consumo. Si los bienes se consumen en cantidades pequeñas,
el costo total puede no ser importante. En otras palabras, si el
gasto en esos bienes es pequeño en relación con el ingreso del
consumidor, el costo puede ser despreciable y por lo tanto el
cambio de precio puede que no afecte la demanda. Ejemplo de
esta situación es el consume de la sal de mesa en un hogar.
2. Ingreso. Si el ingreso es alto en relación con el precio del bien
(más precisamente, si el costo del consumo es bajo en relación
con el ingreso), el aumento en el precio del bien puede que no
afecte la demanda. Como un ejemplo se puede mencionar otra
vez la sal de mesa, cuyo precio es relativamente bajo, aun para
los hogares de bajos ingresos.
3. Sustituibilidad. Si hay libre competencia y existen varios
sustitutos del bien, la demanda se verá afectada por un
aumento en el precio. Mientras más sustitutos haya, mayor
será el efecto de un aumento del precio en la demanda. Otra
vez, la sal de mesa es un buen ejemplo. No tiene buenos
sustitutos y por lo tanto un aumento en su precio no afecta
mucho la demanda.
4. Clase de bienes. Los bienes de lujo, suntuarios o superfluos
pueden verse muy afectados por un aumento de precios,
mientras que los bienes necesarios o de primera necesidad se
afectan menos por un aumento de precio. Un ejemplo es el
consume de pan, panela, agua de la llave, etc. Un aumento en
el precio del agua para consumo doméstico o de la panela
afecta menos su demanda que un aumento en el precio de los
tiquetes aéreos o en el precio de automóvil.
5. Hábitos y tiempo. La elasticidad precio-demanda para bienes
de consumo que han sido aceptados por el mercado hace ya
algún tiempo (y si para el análisis se utiliza una serie de datos
históricos suficientemente larga) será posiblemente baja. Más
aun, cuando se analiza el comportamiento de esos datos para
determinar la elasticidad precio-demanda, hay que tener en
cuenta que el hábito de consumo no cambia de manera
repentina. Lo hábitos de consumo no son fáciles de cambiar.
A continuación se presenta un resumen del comportamiento de la
demanda, dado que ha habido un aumento del precio de los bienes en
estudio. Existen tres casos básicos:
1. Aumento nominal de precio mayor que la tasa de inflación.
2. Aumento nominal de precio igual que la tasa de inflación.
3. Aumento nominal de precio menor que la tasa de inflación.
Suponiendo que el resto de la economía se ajusta por la tasa de inflación (y
en particular el ingreso), se puede decir que en el Caso 1 se detectará una
reducción de la demanda. En el caso 2 no habrá cambios en la demanda y
en el Caso 3 la demanda puede aumentar.
Por el otro lado, se pueden identificar tres clases de bienes:
1. Bienes con demanda elástica o casi elástica.
2. Bienes con elasticidad unitaria
3. Bienes con demanda inelástica.
La Clase 1 es una clase de bienes cuya demanda cambia en una
proporción mayor que el cambio en el precio. La Clase 2 incluye bienes
cuya demanda cambia exactamente lo mismo que el cambio en el precio. Y
la Clase 3 incluye bienes cuya demanda cambia en una proporción menor
a la del cambio de precio. Estos cambios están asociados a un coeficiente
de elasticidad, β. Si el valor absoluto de β es mayor que 1 (Clase 1), igual a
1 (Clase 2) y menos que 1 (Clase 3).
Al usar este coeficiente β en una ecuación lineal, nos permite medir el
efecto del aumento de precios en la demanda. Esta ecuación se llama el
factor de elasticidad.
El factor de elasticidad
El factor de elasticidad tiene en cuenta la elasticidad precio-demanda
propiamente dicha. Con este factor se puede ajustar la demanda
multiplicando la demanda por el factor. Por ejemplo, si se tiene la
demanda del período n, esta debe ajustarse con el factor de elasticidad del
mismo período así:
Dn ajustada = Dn sin ajustar x Factor de elasticidad
Factor de Elasticidad = 1+ elasticidad = 1+β*(aumento real de precio)
Aumento real de precio = (1+aumento en el precio nominal)/(1+inflación)-1
Entonces,
Factor de Elasticidad =
1+β*((1+ aumento en el precio nominal)/(1+inflación)-1)
y
Dn ajustada =
Dn sin ajustar x 1+β*((1+ aumento en el precio nominal)/(1+inflación)-1)
El coeficiente de elasticidad β puede ser un valor mayor o menor que cero.
Este factor de elasticidad se utiliza, como se indicó, para multiplicar una
demanda dada y de esta manera incluir el efecto del aumento de precios
en la demanda. Si se explora la ecuación del factor de elasticidad, cuando
β es 1, y hay un aumento real de precios, la demanda se reducirá en el
mismo porcentaje en que se aumentó el precio de venta. Si β es mayor que
1, la demanda verá afectada en más del porcentaje real de aumento de
precios y finalmente, si β es menor que 1, la demanda se verá afectada en
menos que el porcentaje de aumento real de precios. Entonces, si fijamos a
β en cero, se dice que el bien es completamente inelástico. Esto significa
que el precio puede aumentar y la demanda no se verá afectada. El bien se
consume igual.
Un ejemplo de una función de elasticidad.
Un ejemplo es el del consumo del agua potable en los hogares. Cuando se
construyen funciones de elasticidad, es necesario entender el hábito de
consumo.
En este caso, se utiliza la siguiente función de elasticidad.
Q t = e C Pt −β11 Qtβ−22
(1)
o
ln Qt = C + β 1 ln Pt −1 + β 2 ln Qt − 2
Hay que reconocer que la gente reacciona en cuanto al consumo, cuando
se conoce el Nuevo precio. Sin embargo, también se debe reconocer que los
hábitos son muy difíciles de cambiar. Por esa razón la cantidad
demandada depende no solo del precio, sino del consumo de dos períodos
atrás (se trata del consumo de agua tratada en el acueducto) Nos interesa
el coeficiente de Pt-1 o la pendiente (β) de Pt-1.
Se puede utilizar métodos de regresión lineal con una adecuada serie de
datos y con ello calcular el valor de β. Y en este caso se utiliza β1 como
coeficiente de elasticidad. Este es el coeficiente del precio en la ecuación.
Ejemplo de cálculo de elasticidad de un producto
Se cuenta con la información de consumo de agua residencial en el estrato
5 de la ciudad de Cali, Colombia.
Si la facturación es mensual, el usuario percibe el aumento de precio en
un mes e inicia su cambio de patrón de consumo al mes siguiente. El
patrón de consumo no se cambia de manera instantánea. Puede haber
una gran variedad de modelos que representen este fenómeno. Así mismo,
la demora en el cambio del patrón de consumo se puede representar de
muchas formas.
Una manera de representar el fenómeno puede ser modelando el efecto
sobre el consumo para que dependa del precio del último mes y del
consumo de dos meses atrás. Eso se puede representar en una ecuación
tal como la siguiente:
Q t = e C Pt −β11 Qtβ−22
(1)
Cuando se quieren estimar parámetros de ecuaciones como (1), se pueden
linealizar y expresar como una ecuación lineal. A partir de esta idea se
puede rescribir esta ecuación como
ln Qt = C + β 1 ln Pt −1 + β 2 ln Q
(2)
t −2
Los valores de C, β1 y β2 se pueden encontrar por regresión lineal. Usando
la opción Análisis de datos en Herramientas de Excel, se tiene lo siguiente:
Estrato 5 Cali consumo de agua
Mes Precio m3 $98 Cantidad m3 lnPt-1
ln Qt-2
1
246
30.23
2
243
30.59
3
238
31.37 5.49306 3.40883
4
242
31.14 5.47227 3.42067
5
241
31.25 5.48894 3.44585
6
231
33.04 5.48480 3.43849
7
246
31.64 5.44242 3.44202
8
247
32.06 5.50533 3.49772
9
244
32.44 5.50939 3.45442
10
269
30.2 5.49717 3.46761
11
252
31.99 5.59471 3.47939
12
267
30.55 5.52943 3.40784
13
255
31.71 5.58725 3.46542
14
259
31.11 5.54126 3.41936
15
256
31.3 5.55683 3.45663
16
275
29.33 5.54518 3.43753
17
276
29.09 5.61677 3.44362
18
257
30.97 5.62040 3.37861
19
267
30.16 5.54908 3.37039
20
296
27.8 5.58725 3.43302
21
279
29.01 5.69036 3.40652
22
279
29.05 5.63121 3.32504
23
297
27.86 5.63121 3.36764
24
284
29.05 5.69373 3.36902
25
294
28.03 5.64897 3.32719
26
297
27.57 5.68358 3.36902
27
310
26.49 5.69373 3.33328
28
314
26.19 5.73657 3.31673
29
290
28.03 5.74939 3.27677
30
296
27.5 5.66988 3.26538
31
317
26.09 5.69036 3.33328
32
300
27.38 5.75890 3.31419
33
300
27.03 5.70378 3.26155
34
284
28.3 5.70378 3.30981
35
297
27.49 5.64897 3.29695
36
302
27.22 5.69373 3.34286
37
290
28.18 5.71043 3.31382
38
303
27.27 5.66988 3.30395
39
307
27 5.71373 3.33861
40
314
26.44 5.72685 3.30579
41
307
27.02 5.74939 3.29584
42
312
26.87 5.72685 3.27488
43
296
28.16 5.74300 3.29658
44
291
28.77 5.69036 3.29101
45
284
29.26 5.67332 3.33790
46
307
27.61 5.64897 3.35933
47
306
27.83 5.72685 3.37622
lnQ
3.44585
3.43849
3.44202
3.49772
3.45442
3.46761
3.47939
3.40784
3.46542
3.41936
3.45663
3.43753
3.44362
3.37861
3.37039
3.43302
3.40652
3.32504
3.36764
3.36902
3.32719
3.36902
3.33328
3.31673
3.27677
3.26538
3.33328
3.31419
3.26155
3.30981
3.29695
3.34286
3.31382
3.30395
3.33861
3.30579
3.29584
3.27488
3.29658
3.29101
3.33790
3.35933
3.37622
3.31818
3.32611
Mes Precio m3 $98 Cantidad m3
48
323
26.85
49
309
27.93
50
307
27.96
51
331
26.18
52
317
27.15
53
308
27.65
54
313
27.48
55
320
27.27
56
332
26.62
57
261
31.9
58
324
28.05
59
332
27.17
60
361
25.15
lnPt-1
5.72359
5.77765
5.73334
5.72685
5.80212
5.75890
5.73010
5.74620
5.76832
5.80513
5.56452
5.78074
5.80513
ln Qt-2
3.31818
3.32611
3.29027
3.32970
3.33077
3.26500
3.30138
3.31963
3.31346
3.30579
3.28166
3.46261
3.33399
lnQ
3.29027
3.32970
3.33077
3.26500
3.30138
3.31963
3.31346
3.30579
3.28166
3.46261
3.33399
3.30211
3.22486
Usando en Análisis de datos la opción Regresión, se encuentra lo
siguiente:
Estadísticas de la regresión
Coeficiente de correlación múltiple
Coeficiente de determinación R^2
R^2 ajustado
Error típico
Observaciones
ANÁLISIS DE VARIANZA
Grados de
libertad
Regresión
2
Residuos
55
Total
57
Intercepción
lnPt-1
lnQt-2
0.78792775
0.62083015
0.60704215
0.04197549
58
Suma de
cuadrados
0.15866943
0.0969068
0.25557623
Promedio de los
Valor crítico de
cuadrados
F
F
0.0793347145.0268628 2.6178E-12
0.00176194
Coeficientes Error típico Estadístico t
4.38009751 0.78815565 5.55740165
-0.36926095 0.07983081 -4.62554406
0.31619518
0.119768 2.64006389
Probabilidad
8.2506E-07
2.3117E-05
0.01076563
El coeficiente del precio, en este caso –0.3692 es el coeficiente de
elasticidad, β. Por cada 1% de aumento en el precio, la demanda se reduce
en –0.3692%. Esto se puede expresar en términos de aumento de precios e
inflación de la siguiente manera:
 1 + aumento de precios 
− 1
Factor de elasticidad = 1 - 0.3692
 1 + tasa de inflación

(3)
Si el aumento de precios real (deflactado) es de 1%, entonces la demanda
se reduce en –0.3692%.