sol
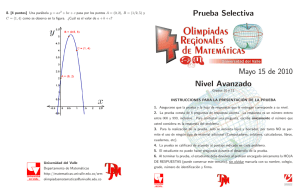
Anuncio

ÁLGEBRA LINEAL I
Algunas soluciones a la Práctica 2
Combinatoria
(Curso 2015–2016)
5.– ¿Cuántos números de cinco cifras tienen todas ellas diferentes?.
La primera cifra puede ser cualquiera menos el 0: nueve posibilidades. La segunda
cualquiera menos la anterior: nueve posibilidades. La tercera cualquiera menos las
dos primeras: ocho posibiliades. Reiterando el argumento queda:
9 · 9 · 8 · 7 · 6 = 27216.
10.– Consideramos el alfabeto formado por las diez letras A,B,C,D,E,F,G,H,I,J.
(i) ¿Cuántas ”palabras” de 3 letras pueden formarse con todas ellas distintas y en orden
alfabético?.
Para formar una palabra de tres letras distintas en orden alfabético basta seleccionar
que tres letras diferentes la formaran (necesariamente habrá una única forma de
colocarlas en orden alfabético). Por ejemplo si seleccionamos A,G,C la palabra de tres
letras en orden alfabético serás ACG. Igualmente si seleccionamos C,A,G la palabara
de tres letras en orden alfabético es ACG.
En definitiva hemos de contar cuantos grupos puden formarse de tres elementos
diferentes escogidos entre diez posibles sin importar el orden. Son combinaciones
sin repetición de 10 elementos tomados de 3 en 3:
10
10!
10 · 9 · 8
C10,3 =
=
=
= 120.
3
3!(10 − 3)!
1·2·3
(ii) ¿Cuántas ”palabras” de 8 letras que tengan exactamente tres Aes.?
Primero contamos en que tres posiciones de las ocho posible aparecerán las tres Aes.
Son formas de elegir tres elementos entre ocho posibles sin importar el orden y sin
repetir: C8,3 .
Después contamos las formas de colocar cinco letras escogidas entre las nueve restantes
en los cinco puestos que han quedado libres. Son variaciones con repetición de 9
elementos tomados de 5 en 5. En total:
8
8!
8·7·6 5
C8,3 · V R9,5 =
· 95 =
· 95 =
· 9 = 3306744
3
(8 − 3)!3!
1·2·3
¿Cuántas de ellas tienen las tres Aes consecutivas?.
Ahora las Aes necesariamente aparecen consecuitvas.
posiciones distintas:
Pueden ubicarse en seis
AAAXXXXX,XAAAXXXX,XXAAAXXX,
XXXAAAXX,XXXXAAAX,XXXXXAAA
Por cada una de ellas, como antes, contamos las formas de colocar las cinco letras en
los puestos libres escogidas entre nueve posibles. En total:
6 · V R9,5 = 6 · 95 = 354294.
11.– Se reparten 10 canicas entre tres niñas, Sabela, Lorena y Rita.
(i) ¿De cuántas formas puede hacerse si las canicas son todas diferentes entre si?.
Supongamos que las diez canicas están numeradas del 1 al 10. Un reparto de las
mismas consiste en asignar a cada número uno de los tres posibles nombres de las
niñas. Es decir, estamos contando cuantos grupos de 10 elementos podemos formar
con 3 diferentes pudiendo repetirlos e importando el orden. Se trata de variaciones
con repetición de 3 elementos tomados de 10 en 10:
V R3,10 = 310 .
(ii) ¿De cuántas formas puede hacerse si las canicas son indistinguibles entre si?.
La diferencia con el caso anterior es que ahora, por ser indistinguibles las canicas, da
igual que canica toque a cada una; un reparto sólo se diferencia de otro en el número
de canicas que toco a cada una. Se trata por tanto de contar cuantos grupos de 10
elementos podemos formar con 3 diferentes, pudiendo repetirlos pero sin importar el
orden. Son combinaciones con repetición de 3 elementos tomados de 10 en 10:
3 + 10 − 1
12
12
CR3,10 =
=
=
= 66.
10
10
2
¿Y si además cada niña recibe al menos dos canicas?.
Si cada una recibe dos canicas al menos, quedan por repartir 10 − 2 · 3 = 4 canicas.
Son combinaciones con repetición de 3 elementos tomados de 4 en 4:
3+4−1
6
6
CR3,4 =
=
=
= 15.
4
4
2
12.–
(i) ¿Cuántas matrices distintas 3 × 3 pueden formarse con 6 unos y 3 ceros?.
(ii) ¿Cuántas de ellas tienen traza impar?.
Dado que las matrices sólo están formados por ceros y unos, la traza será impar si
tiene un uno y dos ceros o tres unos. Calculamos cuantas matrices hay de cada tipo
y sumamos los resultados.
- Matrices con un uno y dos ceros en la diagonal. Hay tres posibilidades para situar el
uno en la diagonal. Por cada una de ellas contamos las formas de distribuir los cinco
unos y el cero restantes, en las otras seis posiciones de la matriz. Razonando como en
(i) son P R6;5,1 ó C6,1 . En definitiva:
3 · P R6;5,1 = 3 ·
6!
= 18.
5!1!
- Matrices con tres unos en la diagonal. Simplemente hay que contar las formas de
distribuir los tres ceros y tres unos restantes fuera de la diagonal. Razonando como
en (i) son P R6;3,3 ó C6,3 :
6
6·5·4
P R6;3,3 = C6,3 =
=
= 20.
3
1·2·3
En total:
20 + 18 = 38.
13.– Un test consta de 10 preguntas con una única respuesta correcta de entre 4 posibles.
(i) ¿Cuántos test distintos se pueden cubrir con 6 respuestas falladas y 4 acertadas?.
Las distintas formas en que pueden ubicarse las seis respuestas falladas, son las formas
de elegir seis preguntas de entres las diez totales, sin importarnos el orden y sin repetir:
10 · 9 · 8 · 7
10
.
C10,6 =
=
1·2·3·4
6
Ahora cada una de esas repuestas puede haber sido contestada de tres formas
diferentes; las cuatro respuestas acertadas por el contrario sólo pueden haberse
contestado marcando la respuesta correcta. Por tanto el número total de test distintos
es:
10 · 9 · 8 · 7 6
C10,6 · 36 =
· 3 = 153090.
1·2·3·4
(ii) ¿Cuántos con 2 respuestas acertadas, 3 falladas y 5 en blanco?.
Para seleccionar las tres falladas tenemos C10,3 posibilidades. Para las cinco en blanco
escogemos cinco entre las siete restantes: C7,5 . Finalmente las arcetadas y en blanco
sólo pueden cubirise de una manera; mietnras que las falladas tienen cada una de ellas
tres respuestas posibles. Por tanto el número de test en las condicioens indicadas será:
10 · 9 · 8 7 · 6
C10,3 C7,5 · 33 = C10,3 C7,2 · 33 =
·
· 68040.
1·2·3 1·2
(iii) Generaliza el apartado anterior para un test de n preguntas con una única respuesta
correcta de entre 4 posibles, y con f respuestas falladas, a respuestas acertadas y el
resto en blanco.
Repitiendo el argumento anterior tenemos:
Cn,f · Cn−f,n−f −a
· 3f
= Cn,f · Cn−f,a
· 3f
n n−f f
=
3 .
f
a
(1 punto)
ÁLGEBRA LINEAL I
Solución a los problemas adicionales
Combinatoria
(Curso 2015–2016)
I.– Siete personas suben en un ascensor en la planta baja de un edificio de cinco pisos.
Cada una de ellas se apea en alguna de las cinco plantas.
(i) ¿De cuántas formas pueden bajarse si distinguimos quien se baja en cada piso?.
Cada posiblle forma de bajarse puede representarse por un grupo ordenado de siete
números cada uno de ellos elegido del 1 al 5 que indica en que piso se bajó cada uno
de los individuos. Por tanto se trata de contar cuantros grupos de 7 elementos pueden
formarse elegidos entre 5 posibles, de manera que importa el orden y puede repetirse.
Son variaciones con repetición:
V R5,7 = 57 = 78125.
(ii) ¿De cuántas formas pueden bajarse si no distinguimos quien se baja en cada piso, sino
únicamente cuántas personas se bajan en cada uno de ellos?.
La diferencia con el caso anterior es que ahora no importa en que orden se escriban los
pisos en los que bajan los individuos, ya que no importa la persona que se bajó en cada
uno de ellos. Se trata ahora de contar cuantros grupos de 7 elementos pueden formarse
elegidos entre 5 posibles, de manera que NO importa el orden y puede repetirse. Son
combinaciones con repetición:
5+7−1
11
7
CR5,7 = 5 =
=
= 330
7
7
II.– Vives en una urbanización que se puede representar esquemáticamente con el siguiente
diagrama:
Una mañana te dispones a desplazarte desde A hasta B. Es claro que para hacerlo
tendrás que recorrer al menos 11 tramos (un “tramo” es la longitud del lado de una
manzana).
(a) ¿Cuantos recorridos formados por 11 tramos llevan desde A hasta B?
Para hacer el recorrido en once tramos necesariamente en cada cruce sólo puedes, o
bien subir, o bien ir a la derecha. Si bajas o vas a la izquierda necesitarı́as más de 11
tramos para completar el recorrido. En concreto hay que subir 4 manzanas e ir 7 a la
derecha.
Por tanto una ruta de once tramos consiste simplemente en decidir en que orden
hacemos los tramos de subida y los de ir a la derecha. Son permutaciones con repetición
de 11 elementos donde hay 7 de una clase y 4 de la otra:
P (11; 7, 4) =
11!
= 330
7!4!
(b) ¿Cuántos de 12 tramos?
Sabemos que el número mı́nimo de tramos es 11, 4 hacia arriba y 7 a la derecha.
Si recorremos algún tramo a la izquieda o hacia abajo, hemos de volver a recorrer
otro hacia la derecha o hacia arriba respectivamente, para recuperalo. Por tanto para
completar el recorrido de A a B, necesariamente hemos de añadir un número par de
tramos al número mı́nimo 11. Deducimos que es imposible hacerlo en 12 tramos.
(c) Si deseas evitar a toda costa la intersección C marcada en el dibujo (por motivos que
no vienen al caso), ¿cuántos recorridos de 11 tramos puedes seguir?
Contamos el número de recorridos de 11 tramos que pasan por la intersección C y los
descontamos del número de recorridos total calculado en (a).
Para ir de A a C necesitamos 3 tramos a la derecha y 2 hacia arriba. Las posibilidades
son P (5; 3, 2). Para ir de C a B necesitamos 4 tramos a la derecha y 2 hacia arriba.
Es decir, P (6; 4, 2) posiblidades. En total hay
P (5; 3, 2) · P (6; 4, 2) =
5!
6!
·
= 150
3!2! 4!2!
recorridos de 11 tramos pasando por C.
Por tanto el número de recorridos de 11 tramos que no pasan por C es:
11!
5!
6!
−
·
= 330 − 150 = 180.
7!4! 3!2! 4!2!
III.–
i) ¿En el plano afı́n E2 , cuál es el máximo número de puntos de intersección que producen
12 rectas distintas?.
Cada par de rectas no paralelas nos produce un punto de intersección. El número
máximo de puntos aparece por tanto cuando no hay ningún par de rectas paralelas y
hay tantos puntos como formas de agrupar de dos en dos las rectas:
C12,2 =
12
12 · 11
=
= 66.
1·2
2
ii) ¿Y si hay al menos cinco rectas paralelas entre si?.
Si hay cinco rectas paralelas, cualquier par de ellas no determinan un punto de
intersección. Por tanto al número calculado en el apartado anterior hay que descontar,
los pares de rectas que se pueden formar con las cinco paralelas:
12
5
C12,2 − C5,2 =
−
= 66 − 10 = 56.
2
2
iii) ¿Y si las rectas contienen a los lados de un dodecágono regular?.
En este caso los lados opuestos del dodecágono son paralelos; por tanto hay total
de puntos calculado en el primer apartado hay que descontar los seis pares de rectas
paralelas que no producen puntos de intersección:
66 − 6 = 60.
IV.– Sea A un conjunto con n elementos. ¿Cuántos subconjuntos tiene el conjunto A?.
Probar que el número de subconjuntos de cardinal par y el número de subconjuntos de
cardinal impar coinciden.
Método I: Dado un subconjunto de A cada elemento puede estar o no en el
subconjunto. Es decir hay dos posibilidades para cada elemento de A. Por tanto,
en total habrá 2n posibles subconjuntos.
Veamos ahora que coinciden el número de subconjuntos de cardinal par e impar. Para
ello definiremos un criterio que hace corresponder a cada conjunto con un número par
de elementos otro con un número impar, y viceversa. Fijamos un elemento a0 ∈ A.
Dado un subconjunto B de A, construimos un subconjunto B 0 de la siguiente manera:
{no par de elementos}
B
{no impar de elementos}
B ∪ {a0 } si a0 6∈ B
−→
B \ {a0 } si a0 ∈ B
−→
Es decir, si a0 no está en B, se lo añadimos (B 0 = B ∪ {a0 }); si a0 está en B se lo
quitamos (B 0 = B \ {a0 }). De esta forma establecemos una correspondencia biunı́voca
entre subconjuntos de A con un número par de elementos y subconjuntos de A con un
número impar de elementos. Por tanto hay el mismo número de unos y de otros.
Método II: El número de subconjuntos de k elementos que tiene A corresponde
precisamente
a las combinaciones sin repetición de n elementos tomado de k en k,
Cn,k = nk . El número total de subconjuntos será:
n
n
n
T otal = Cn,0 + Cn,1 + . . . + Cn,n =
+
+ ... +
0
1
n
Pero por el binomio de Newton esto es exactamente (1 + 1)n = 2n .
Con este mismo razonamiento el número de subconjuntos con un número par de
elementos es:
n
n
n
P ares = Cn,0 + Cn,2 + . . . + Cn,m =
+
+ ... +
0
2
m
donde m = n si n es par y m = n − 1 si n es impar. El número de subconjuntos con
cardinal impar es:
n
n
n
Impares = Cn,1 + Cn,3 + . . . + Cn,m0 =
+
+ ... +
1
3
m0
donde m0 = n − 1 si n es par y m0 = n si n es impar. Si ahora calculamos la diferencia
entre ambos queda:
n
n
n
n
n
n
n
P ares − Impares =
−
+
−
+
+ . . . + (−1)
n
0
1
2
3
4
Por el binomio de Newton esto es exactamente (1 − 1)n = 0 y probamos la igualdad
entre P ares e Impares.
V.–
(i) ¿Cuántas matrices 3 × 3 pueden fomarse con tres unos, tres doses y tres treses?.
Tenemos que contar las formas de distribuir nueve elementos en nueve posiciones
distintas, de los cuales 3, 3, 3 son iguales entre si. Por tanto son permutaciones con
repetición:
9!
P R9;3,3,3 =
= 1680.
3!3!3!
(ii) ¿Cuántas de ellas tienen traza mayor o igual que siete?.
La traza se obtiene sumando los términos de la diagonal. Dado que la matriz está
formada por unos, doses y treses, la diagonal sumará siete o más, cuando en la digaonal
aparecen: 1 + 3 + 3, 2 + 2 + 3, 2 + 3 + 3, 3 + 3 + 3.
Para cada uno de esos cuatro casos contamos las formas de ubicar los número de la
diagonal y el resto.
- Para 1 + 3 + 3 en la diagonal colocamos un uno y dos treses: P R3;2,1 . Fuera de la
diagonal dos unos, tres doses y un tres. P R6;2,3,1 . En total:
P R3;2,1 · P R6;2,3,1 =
3!
6!
·
= 180.
2!1! 2!3!1!
- Para 2 + 2 + 3 en la diagonal colocamos dos doses y un tres: P R3;2,1 . Fuera de la
diagonal tres unos, un dos y dos treses. P R6;3,1,2 . En total:
P R3;2,1 · P R6;3,1,2 =
3!
6!
·
= 180.
2!1! 3!1!2!
- Para 2 + 3 + 3 en la diagonal colocamos un dos y un dos treses: P R3;2,1 . Fuera de
la diagonal tres unos, dos dos y un tres. P R6;3,2,1 . En total:
P R3;2,1 · P R6;3,2,1 =
3!
6!
·
= 180.
2!1! 3!2!1!
- Para 3 + 3 + 3 en la diagonal colocamos tress treses: P R3;3 . Fuera de la diagonal
tres unos, tres doses. P R6;3,3 . En total:
P R3;3 · P R6;3,3 =
3! 6!
·
= 20.
3! 3!3!
En total:
180 + 180 + 180 + 20 = 560.
(iii) ¿Cuántas tienen rango 1?.
Para que tengan rango 1 todas las filas han de ser proporcionales. La única posibilidad
en este caso es que todas las filas o todas las columnas tengan los mismos elementos.
El número de matrices con todas las filas con el mismo elemento, es el número de formas
de ordenar las filas (1, 1, 1), (2, 2, 2) ,(3, 3, 3). Son permutaciones de 3 elementos. Lo
mismo para las columnas. Por tanto el número total de matrices de rango 1 es:
3! + 3! = 6 + 6 = 12.
VI.–
(a) ¿De cuántas maneras pueden entrar diez alumnos en tres aulas, si no se hace distinción
de personas?
Método I: Para contar cuántas posibilidades hay podemos tener en cuenta lo
siguiente. Escribimos un número del 1 al 3 por cada uno de los alumnos, dependiendo
de en qué clase ha entrado. Estamos formando por tanto grupos de 10 elementos
escogidos de entre 3 posibles.
Como dos alumnos pueden entrar en la misma clase, pueden repetirse elementos.
Como no distinguimos entre los alumnos, no nos importa el orden en que escribimos
los 10 números del 1 al 3.
Se trata por tanto de combinaciones con repetición de 3 tipos de elementos tomados
de 10 en 10:
3 + 10 − 1
12
12 · 11
= 66.
CR3,10 =
=
=
1·2
10
2
Método II: Contamos de la siguiente manera.
- Si en la clase 1 no entra ningún alumno, los 10 entrarán en las dos restantes
distribuidos:
10 − 0;
9 − 1;
8 − 2;
...
0 − 10;
⇒ 11 posibilidades.
- Si en la clase 1 entra 1 alumno, los 9 restantes podrán distribuirse:
9 − 0;
8 − 1;
7 − 2;
...
0 − 9;
⇒ 10 posibilidades.
Reiterando este argumento vemos que el número de posibilidades totales es:
11 + 10 + 9 + . . . + 2 + 1 =
11 · (1 + 11)
= 66.
2
(b) ¿Y si sı́ que se distingue entre personas?
Razonamos como antes. La única diferencia es que ahora sı́ distinguimos entre
alumnos. Por tanto si importa el orden en que escribimos los 10 números del 1 al
3.
Se trata de variaciones con repetición de 3 tipos de elementos tomados de 10 en 10:
V R3,10 = 310 = 59049.
(Examen extraordinario, diciembre 2005)
VII.– En un armario tenemos guardados 5 pares de zapatos.
(a) ¿Cuántos grupos distintos de 4 zapatos podemos formar?.
Formamos grupos de 4 zapatos extraı́dos entre 10 posibles. El orden no diferencia un
grupo de otro. Se trata por tanto de combinacione de 10 elementos tomados de 4 en
4:
10
10 · 9 · 8 · 7
C10,4 =
=
= 210.
4
1·2·3·4
(b) ¿Cuántos de ellos contiene al menos dos zapatos del mismo par?.
Contamos los grupos que tienen todos los zapatos de pares distintos y se los restamos
al total. El número de formas de seleccionar los cuatro pares de los cuales extraeremos
un zapato es:
C5,4 = 5.
Por cada una de estas selecciones, todavı́a pueden tomarse el zapato izquierdo o el
derecho de cada par:
5 · 24 .
Finalmente, el número de grupos con al menos dos zapatos del mismo par es:
210 − 5 · 24 = 130.
(c) ¿Cuántos de ellos contienen exactamente dos zapatos del mismo par?.
Las distintas formas de escoger el par completo que estará en el grupo son:
C5,1 = 5.
Los dos zapatos restantes petenecerán a pares distintos de los 4 que nos quedans; la
formas de seleccionar los pares a los que pertenencen son:
C4,2 = 6.
Y por cada una de esas selecciones, para cada par, podemos escoger el izquierdo o el
derecho.
Por tanto el número de grupos en las condiciones pedidas es:
C5,1 · C4,2 · 22 = 120.
Otra forma de llegar al resultado podrı́a ser restar al número obtenido en el apartado
anterior, los grupos de zapatos que pueden formarse con dos pares. Para ello sólo hay
que contar las distintas formas de escoger dos pares de entre los cinco posibles: C5,2 .
Nos quedarı́a entonces:
130 − C5,2 = 120.
VIII.– Se dispone de 10 candados con sus correspondientes 10 llaves. Además hay una llave
maestra adicional que abre cualquiera de ellos. Se cierra una caja con dos de esos
candados.
(a) ¿Cuántos grupos distintos de 4 llaves pueden formarse?.
Tenemos en total 11 llaves. Cada grupo se forma escogiendo 4 de ellas, sin repetirlas y
sin importarnos el orden en que lo hacemos. Se trata de combinaciones sin repetición
de 11 elementos tomados de 4 en 4:
11
11 · 10 · 9 · 8
C11,4 =
=
= 330.
4
1·2·3·4
(b) ¿Cuántos de ellos nos aseguran poder abrir la caja?.
Podremos abrir la caja si:
1) En nuestro grupo de 4 llaves está la maestra.
2) En nuestro grupo de 4 llaves no está la maestra pero si las dos llaves que abren los
dos candados.
Contamos cada uno de ellos:
1) Un grupo de 4 donde está la maestra se forma escogiendo 3 llaves de entre las 10
restantes:
10
10 · 9 · 8
C10,3 =
=
= 120.
3
1·2·3
2) Un grupo de 4 donde están las dos de la caja pero no la maestra se forma escogiendo
2 llaves de entre las 8 restantes:
8
8·7
C8,2 =
=
= 28.
2
1·2
En total:
C10,3 + C8,2 = 148.
(c) ¿Con cuántos de ellos podremos abrir al menos uno de los dos candados?.
Contamos con cuantos grupos no podemos abrir ningún candado.
formados con las 8 llaves que no abren ninguno:
Serán grupos
8·7·6·5
8
C8,4 =
=
= 70.
4
1·2·3·4
Los que abren al menos uno, serán el resto:
C11,4 − C8,4 = 330 − 70 = 260.
(Examen extraordinario, septiembre 2008)
IX.– Dados 6 números positivos y 5 negativos. De cuantas maneras pueden escogerse cuatro
de ellos para que su producto sea un número positivo, si
(a) no pueden repetirse.
Para que el producto de cuatro números sea positivo, las opciones son:
i) Los cuatro positivos.
ii) Dos positivos y dos negativos.
iii) Los cuatro negativos.
Además, en todo caso, no podemos repetir los números dados y no importa el orden
en el cual hagamos el producto. Las posibilidades son:
i) Los cuatro positivos. Combinaciones sin repetrición de 6 elementos tomados de 4
en 4:
6
6!
= 15.
C6,4 =
=
4
4!2!
ii) Dos positivos y dos negativos. Combinaciones sin repetición de 6 elementos tomados
de 2 en 2 por las combinaciones de 5 elementos tomados de 2 en 2:
6 5
6! 5!
C6,2 C5,2 =
=
= 150.
2 2
4!2! 3!2!
iii) Los cuatro negativos. Combinaciones sin repetición de 5 elementos tomados de 4
en 4:
5
5!
C5,4 =
=
= 5.
4
4!1!
En total:
15 + 150 + 5 = 170.
(b) pueden repetirse.
El razonamiento es exactamente el mismo, con la única diferencia de que ahora
podemos repetir elementos. Por tanto usaremos combinaciones con repetición:
i) Los cuatro positivos.
CR6,4 =
6+4−1
9!
=
= 126.
4
4!5!
ii) Dos positivos y dos negativos.
6+2−1 5+2−1
7! 6!
CR6,2 CR5,2 =
=
= 315.
2
2
5!2! 4!2!
iii) Los cuatro negativos.
CR5,4 =
5+4−1
4
=
8!
= 70.
4!4!
En total:
126 + 315 + 70 = 511.
X.– Una fruterı́a vende peras, manzanas, naranjas y plátanos, en bandejas de 6 piezas de
frutas, por ejemplo: una bandeja con 6 manzanas; o con 3 naranjas, 2 peras y un
plátano.
(a) ¿Cuántos tipos de bandejas son posibles?.
Para cada bandeja formamos grupos de seis elementos escogidos entre cuatro tipos
distintos, pudiendo repetirlos. Se trata de combinaciones con repetición de cuatro
elementos tomados de seis en seis:
4+6−1
9
9
CR4,6 =
=
=
= 84.
6
6
3
(b) ¿Cuántos con al menos una fruta de cada clase?.
Si al menos hay una fruta de cada clase, sólo tenemos que contar de cuantas formas
podemos elegir las dos restantes. Análogamente al apartado anterior, serı́an:
4+2−1
5
CR4,2 =
=
= 10.
2
2